Nonisospectral effects on generating localized waves

Abdselam Silem，Hua Wu and Da-jun Zhang

Department of Mathematics，Shanghai University，Shanghai 200444，China

Abstract In this paper we explain how space-time localized waves can be generated by introducing nonisospectral effects which are usually related to non-uniformity of media.The nonisospectral Korteweg–de Vries，modified Korteweg–de Vries and the Hirota equations are employed to demonstrate the idea.Their solutions are presented in terms of Wronskians and double Wronskians and space-time localized dynamics are illustrated.

Keywords: nonisospectral effects，space-time localized wave，integrable system，bilinear

1.lntroduction

In recent decades rogue waves have received intensive attention from both sides of mathematics and physics.Rogue waves are characterized as the waves that ‘appear from nowhere and disappear without a trace’and whose amplitude are relatively large[1–3].Most of models to describe rogue waves are nonlinear Schrödinger (NLS)-type equations，which are complex models and whose solutions are considered as wave packets.Usually，the mechanism to generate rogue waves is via‘resonance’procedure and the resulted solutions are algebraic rational solutions [4–7](also see a recent review [8] and the references therein).

There are other types of equations to describe rogue waves.For example，the modified Korteweg–de Vries (mKdV)equation[9，10]which is used to model water waves with higher nonlinearity near the sea coast.Recently，the complex KdV equation is also employed (by its wave packets) to describe formation of rogue waves in shallow water[11，12]，as the KdV equation is a shallow-water model.All these solutions used to depict rogue waves of the aforementioned equations are rational solutions which can be obtained via a limit(resonant)procedure.

Rogue waves are the waves that are localized in both space and time.Apart from rational solutions，such type of space-time localized waves can also be generated from solitary waves in nonuniform media where integrable models are nonisospectral equations (see [13，14]).Known examples are the nonisospectral NLS equation [15] and its discrete version [16]，the nonisospectral Manakov system [17]，the nonisospectral Kadomtsev–Petviashvili(I) equation [18]，and the complex nonisospectral mKdV equation [19]，etc.

It is possible to generate space-time localized waves by introducing suitable nonisospectral effects.Let us explain the idea by taking the KdV equation as an example.The KdV equation reads

and its 1-soliton solution is

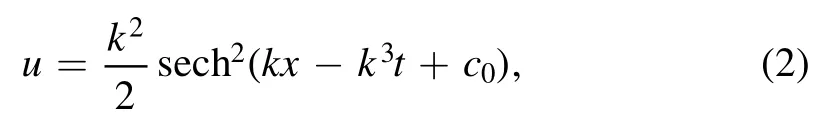
where c0is a constant，k is associated with the Schrödinger spectral problem-φxx+uφ=λφ by λ=-k2.In the isospectral case，k is a constant and generates a standard soliton with an amplitude independent of t，while in the nonisospectral case λ is time-dependent (and so is k).If introducing time-dependence for λ as

where α is a function of t，it is possible to get k(t)such that the amplitudedecays when |t|→∞.Thus，the corresponding nonisospectral KdV (nKdV) equation provides a solitary wave with space-time localness.

In this paper，to explore and demonstrate our idea，we employ the following three integrable equations，namely，the nKdV equation

and，respectively，the nonisospectral mKdV equation and the nonisospectral Hirota equation

where u and q are functions of x and t，α is a function of t.The advantage that equations (4)–(6) are integrable allows that α can be arbitrary.In this circumstance，we take α such a function of t so that we can create a space-time localized solitary wave.Equation (4) is related to the KdV equation with loss and nonuniformity terms [14]，but in our case we allow α depends on t to describe nonuniformity and relaxation of the media dependent of t.Equation (5) is a nonisospectral counterpart of the known mKdV equation with variety of physics backgrounds (see [20] and the references therein).While the third equation (6) is literarily called the Hirota equation with nonisospectral terms，and it is clearly a hybrid of the nonisospectral NLS equation and the nonisospectral complex mKdV equation.Note that Hirota introduced the isospectral version of (6) in [21]，and it shares the same physical meaning with the celebrated NLS equation as it is applicable in the optics fibers and water waves，taking into account the third-order dispersion and a time-delay correction to the cubic nonlinearity.

Remark:Note that all these three equations correspond to a time-dependent spectral parameter that evolves like (3)，which means they can be gauge-transformed to their isospectral counterparts.However，apart from that，we are interested in how nonisospectral effects result in space-time localized (rogue-wave-type) waves，considering some physically meaningful equations (e.g.the Gross–Pitaevskii (GP)，see[22]and the references therein)are related to such type of equations，and also considering the nonisospectral element α(t) represents nonuniformed media (see [13，14])，it is not trivial to investigate solutions and dynamics of such type of equations.

Due to universality，we take the nKdV equation (4) as our example for the investigation.We employ the Hirota bilinear method，and give the solutions in Wronskian form.The fact of classification of the solutions of the KdV and mKdV equation in Wronskian form [20，23] helps to understand the nonisospectral effects.

The outline of this paper is as follows.In section 2 we give integrable background for the three nonisospectral equations.In section 3 we derive solutions of these three equations using bilinear approach and solutions are presented in terms of Wronskians and double Wronskians.Space-time localized dynamics are also illustrated in this section.Finally，section 4 is devoted to conclusions.

2.lntegrable nonisospectral equations

In this section we explain with a bit details how equations (4)–(6) arise from time-dependent spectral parameters，and therefore they are integrable.One can also refer to[24] for generic case.

2.1.Nonisopectral KdV equation

In order to derive a nKdV equation，let us first recall the Schrödinger spectral problem

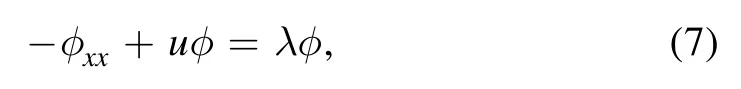
where u=u(x，t) is a potential function and λ is the spectral parameter.The time evolution of φ is

where A，B are two scalar functions independent of φ.The compatibility conditiongives rise to the following equations

Eliminating A，we have

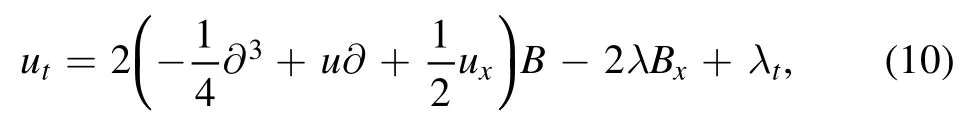
where α=α(t) is some function of t，and

it follows from equation (10) that

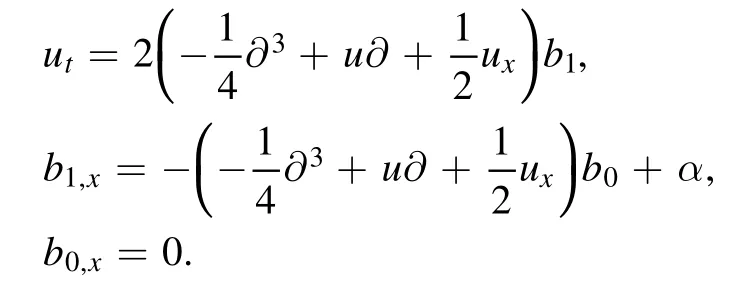
We take b0=4 and consequently，we get b1=-2u+αx，and therefore

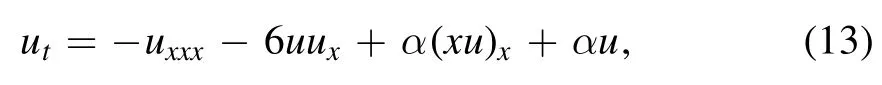
i.e.the nKdV (4).

2.2.Nonisospectral mKdV equation and Hirota equation

Consider the Zakharov–Shabat–Ablowitz–Kaup–Newell–Segur (ZS-AKNS) linear problems [25，26]

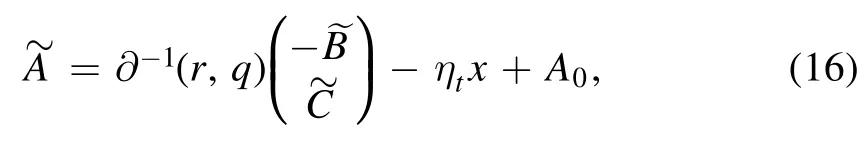
and

Here A0is an integration constant independent of x，and

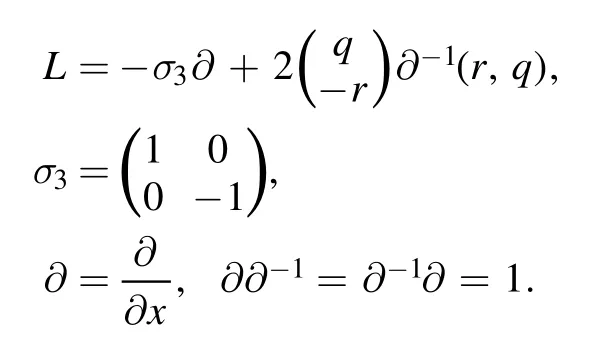
To obtain evolution equations，we use the ansatz

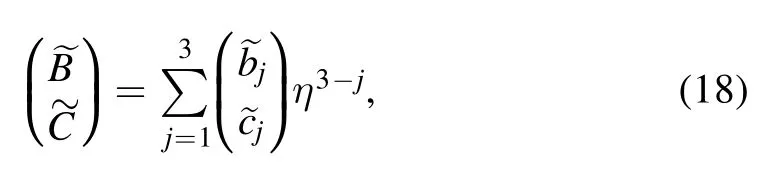
and substitute it into (17).In our case we take

where α is a real function of t，and by letting A0=-4η3andwe work out

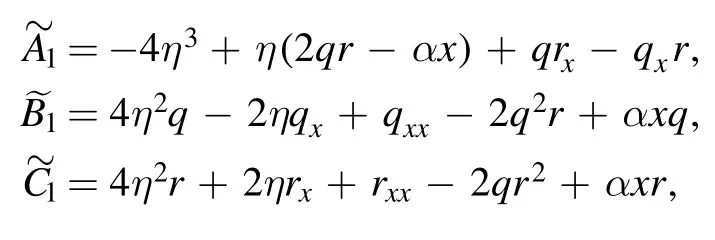
and accordingly，it gives rise to the following 3rd-order AKNS system

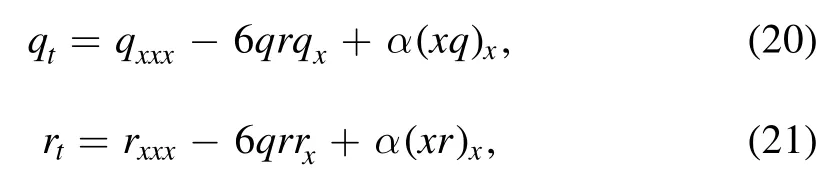
where α is an arbitrary real function of t.It is easy to verify that equations (20) and (21) admit the reduction

which automatically leads (20) to equation (5)，where *stands for the complex conjugate.On the other hand，by letting A0=-4η3+2iη2andwe find out

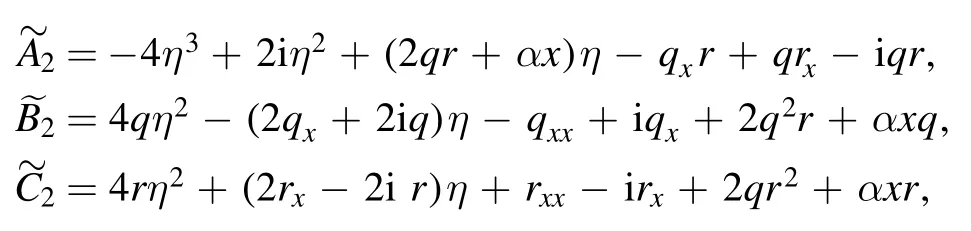
and moreover，the following system is obtained，

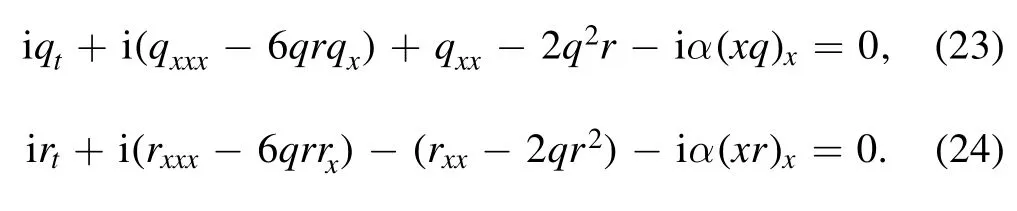
By taking the reduction (22)，consequently，the reduced system gives rise to the nonisospectral Hirota equation (6).

3.Generating localized waves from nonisospectral effects

In this section we demonstrate the nonisospectral effects on generating localized waves，taking equations (4)–(6) as examples.We need to present solutions for these three equations，to achieve which we employ bilinear approach and Wronski determinants.As the KdV equation being one of universal examples in the integrable systems dynamics，we take the nKdV equation (4) as a main example to show the nonisospectral effect on the solutions behavior.Besides，we list the solutions to the equations (5) and (6) with some figures of their waves behavior.

3.1.Nonisopectral KdV equation

3.1.1.Solutions.We employ the notationto denote the Wronskian form established as [27]

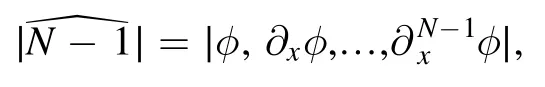
where φ is a Nth order column vector given asφ= (φ1，φ2，… ，φ N)T.For instance，through the transformation

Equation (4) can be transformed to the following bilinear form

where D is the Hirota bilinear operator defined as [28]

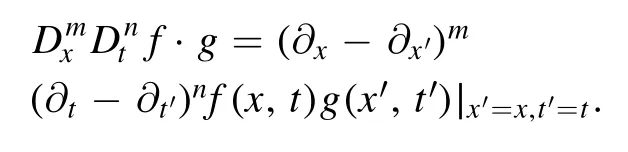
Employing the Wronskian technique，we introduce the following theorem.

Theorem 1.The bilinear form (26) has the following Wronskian solution

where the entry vector φ enjoys the condition

We skip the proof as it is a way similar to [29].

In the following let us list out several explicit forms of φ that meet the condition (28) and we are interested in.

Case 1:Consider

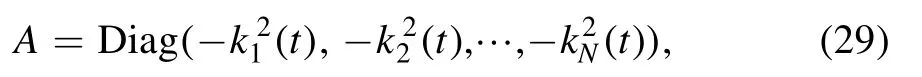
where corresponding to (11) in which λ=-k2，kj(t) should obey the evolution

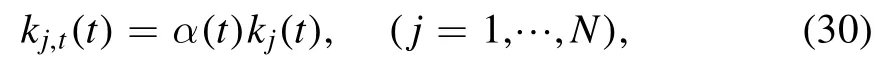
or alternatively

for κ being some function of t such that κ(t)=e∫α(t)dt.Note that for this moment we leave κ(t) (or α(t)) to be open and will choose it later when analyzing time-localized amplitude(see (50)).For such an A，the vector φ satisfying (28) can be defined as

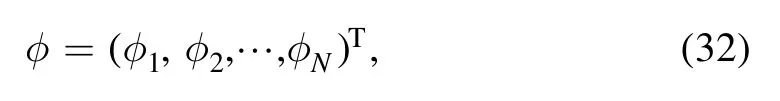
where to obtain solitons，we restrictcj∈R and set 0 ＜c1＜c2＜…＜cNand φjtakes the explicit form

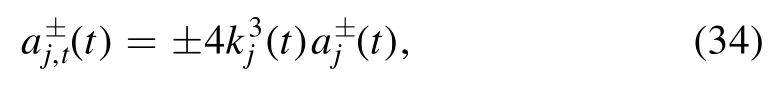
and ξjis defined as

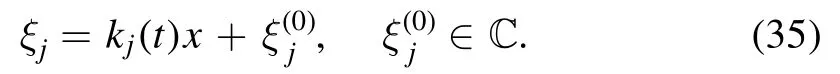
Case 2:Let A be a Jordan block matrix as follows

where k1(t)and κ are defined as in(31).In this case，multiplepole solutions can be obtained.Specially，the Wronskian vector φ can be written in the particular form as(see[20，23])

with

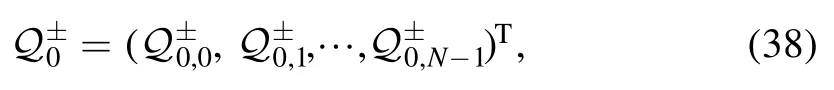
where

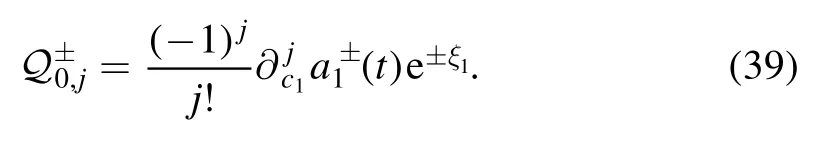
Note that a more general form for φ satisfying (28) can be obtained as the following，

where M ，Nare two Nth order lower triangular Toeplitz matrices (LTTMs)(see [20，23，30])so that(40)contains 2N arbitrary parameters and presents a general solution to (28).

Note that a LTTM of order N is defined as

where aj，j=0，1，…，N-1，are arbitrary complex numbers.All such matrices of order N compose a commutative set.

Case 3:This case yields breathers.Let us consider A taking the form

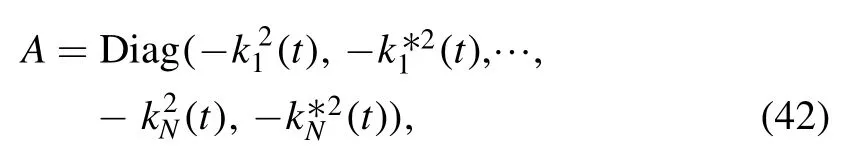
whereis the complex conjugate of kjand each kjis given as(31) withcj∈C.In this case the vector solution to the Wronskian conditions (28) is

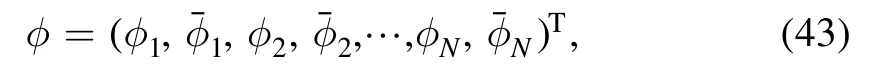
where φjis defined as in (33)，i.e.

andtakes the form

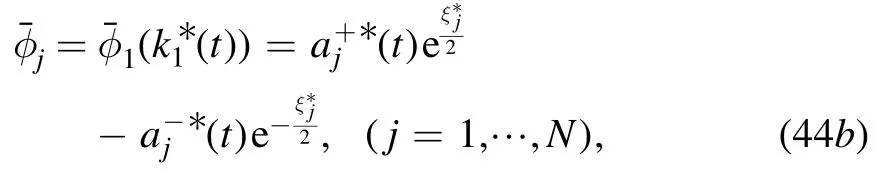
where a±and ξjare，respectively，given as in (34) and (35)，a±*andare their complex conjugates，respectively.

Case 4:Let A be a block Jordan matrix as follows

where

In this case，and for convenience and in practice，we define the Wronskian vector φ as below

where Nth order vector φ is

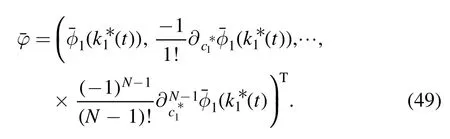
3.1.2.Localized dynamics.We will give a discussion on both solitons and breathers solutions to the equation(4)，with respect to the canonical form of A.

Note that as the equation (4) is Lax-integrable for arbitrary smooth α(t)，in what follows，we consider κ(t) in(31)(or κ2(t))as a Gaussian-variant-type function of t such as

Employing the form of φ in(32)and the taking N=1 in(27)，1-soliton solution reads

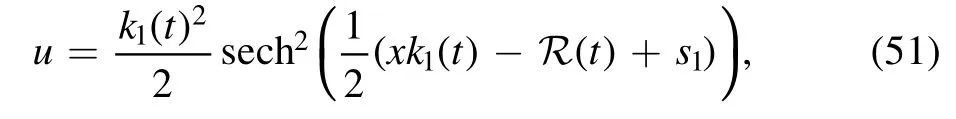
wheres1∈R，

and k1(t) is given as (31).

Taking κ to be as (50a) as an example，the 1-soliton becomes

Obviously，the above solution (52) admits the Gaussian t-variant amplitude as，combining with the soliton part which is in the secant hyperbolic formula that is also Gaussian.Consequently，a localized 1-soliton solution is obtained，as shown in figure 1.Note that the amplitude can be arbitrarily large as c1is arbitrary.

Figure 1.Shape and motion of 1-soliton to the nonisospectral KdV equation (4): (a) a moving localized wave given by (52) for c1=1，s1=0;(b) 2D plot of (a) at t=0.

Through taking N=2，a 2-soliton is corresponding to

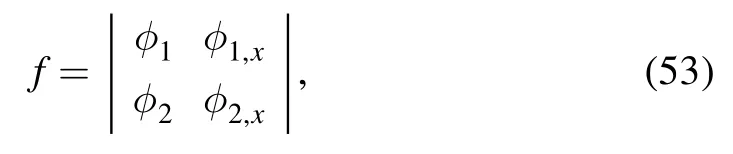
where φj，j=1，2 is defined as (32) with (33).We observe that localized interactions between the two solitons still exist as depicted in figure 2.

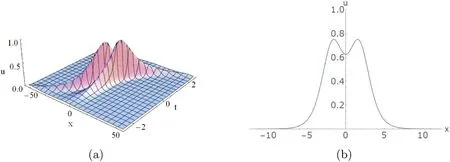
Figure 2.Shape and motion of 2-soliton solution to the nonisospectral KdV equation (4) corresponding to (53): (a) interactions of the two solitons given by (27) corresponding to (53) for k1 with κ taking (50a) and c1=1，c2=1.5，s1=s2=0;(b) 2D plot of (a) at t=0.

One may also consider the wave packet |u|2defined by the complex nKdV equation，which is equation(4)where u is a complex field.Note that the complex isospectral KdV equation and its wave packets have been used to describe rogue waves in shallow water recently [11，12].

In this case，we consider φ taking the form(43)，breathers to equation (4) can be obtained.For instance，the simplest breather corresponds to

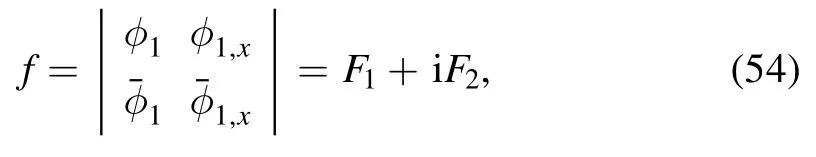
where φ1is given as (33) for k1defined as (31) by assumingc1=a1+ ib1，a1，b1∈R，and

Figure 3 depicts the shape and motion of the breather to the nKdV equation (4).

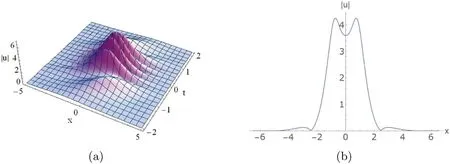
Figure 3.Envelope of breather solution to the nonisospectral KdV equation(4):(a)a breather(25)corresponding to(54)for k1 with κ taking (50a) and c1 = 1.2 +s1=0;(b) 2D interpretation of (a) at t=0.

Finally，we list the 2-breather and the limit-breather solutions.In this circumstance，the both solutions，accordingly，refer to f given by

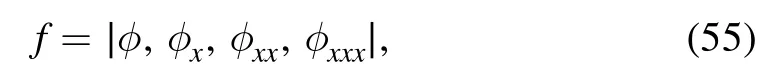
where

and

for the 2-breather solution and the limit breather，respectively，whereφj，are given as(44).Such two breathers interactions and the limit breather behavior are，respectively，depicted in figures 4 and 5.

Figure 4.Envelope of 2-breather solution to the nonisospectral KdV equation (4): (a) 3D interpretation of 2-breather (25) corresponding to(55) with (56) for k1 given by κ taking (50a) and c1=1+i，c2=1.5+i，s1=s2=0.(b) Density plot of (a).

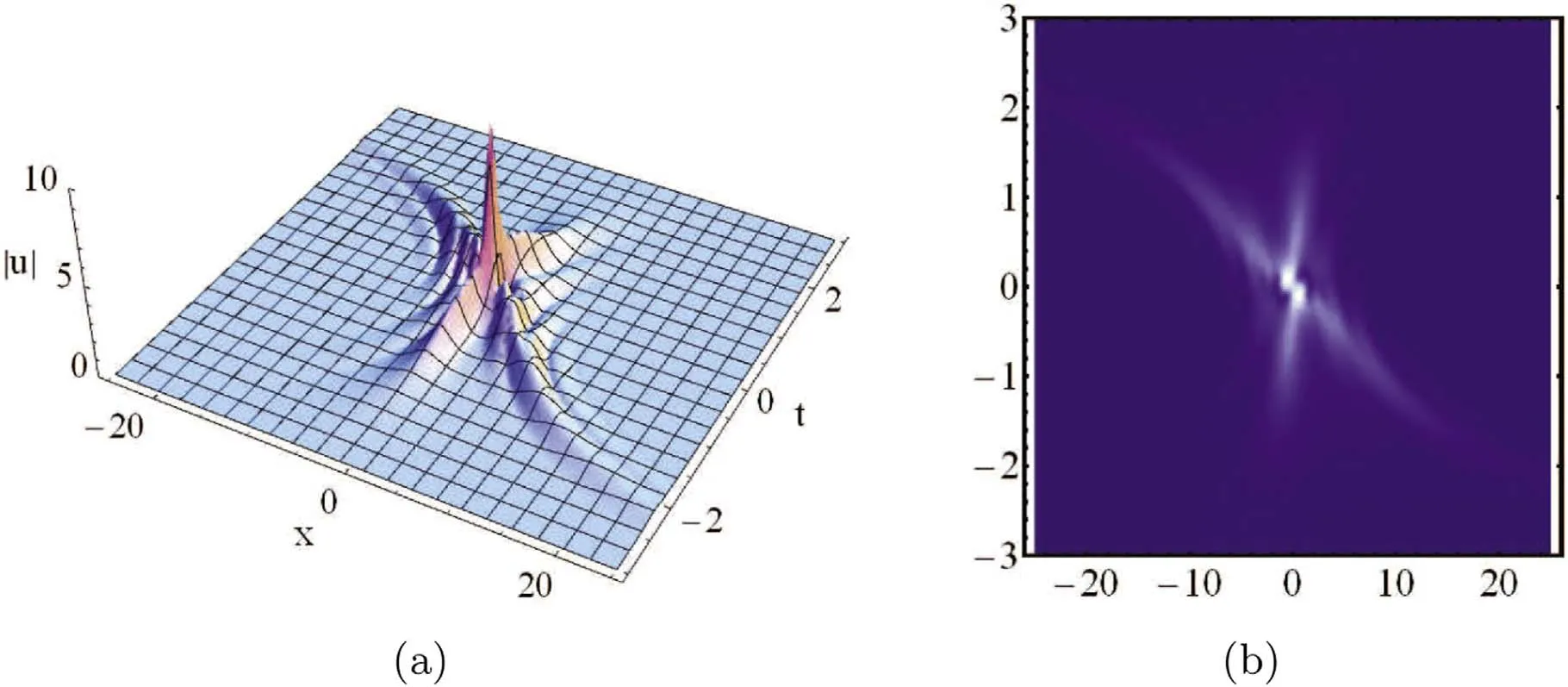
Figure 5.Envelope of limit breather solution to the nonisospectral KdV equation(4):(a)3D interpretation of(25)corresponding to(55)with(57) for k1 given by κ taking (50a) and c1=1+1.2i，s1=0.(b) Density plot of (a).

3.2.Nonisospectral mKdV equation and Hirota equation

In what follow we will introduce the solutions in double Wronskian form for (20) and (23)，discuss their reductions and illustrate dynamics of solutions.

3.2.1.Solutions for the unreduced systems.The unreduced systems equations(20)and(23)can be bilinearized through the rational transformation

as the following，

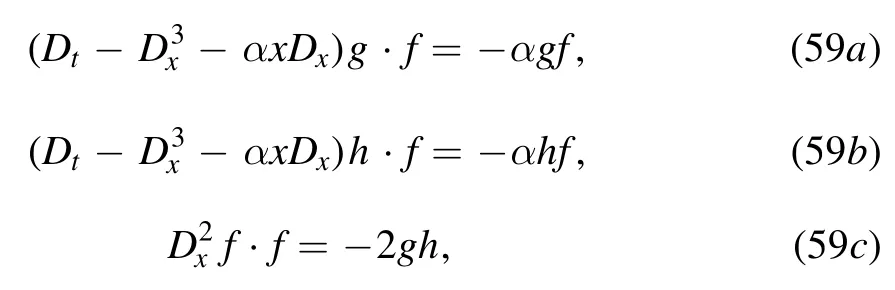
and

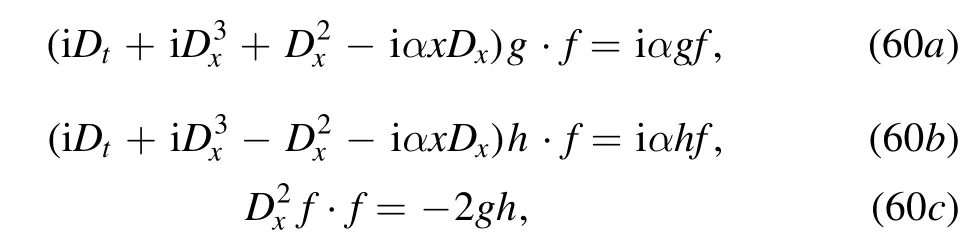
respectively.Recall the double Wronskianformed as [31]

where φ and ψ are (M+N) column vectors given as

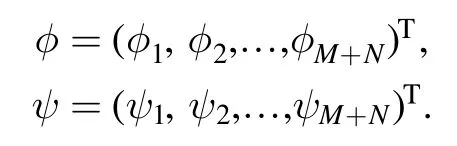
For solutions to the above systems(59)and(60)，we have the following.

Theorem 2.Double Wronskian solutions to the bilinear forms(59) and (60) are given as

Required that the entries φ and ψ meet the condition

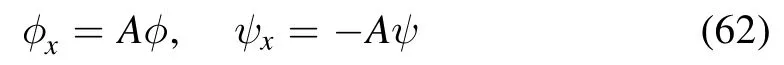
together with

for (59)，and

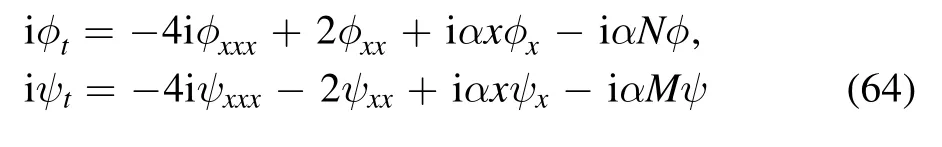
for (60)，respectively.HereA=A(t) is a (N+M)×(N+M) matrix of t but independent of x.

Formal solutions of φ and ψ of the this theorem are

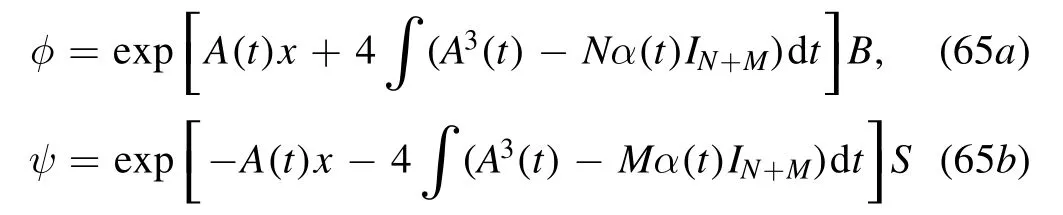
for meeting (62) and (63)，and

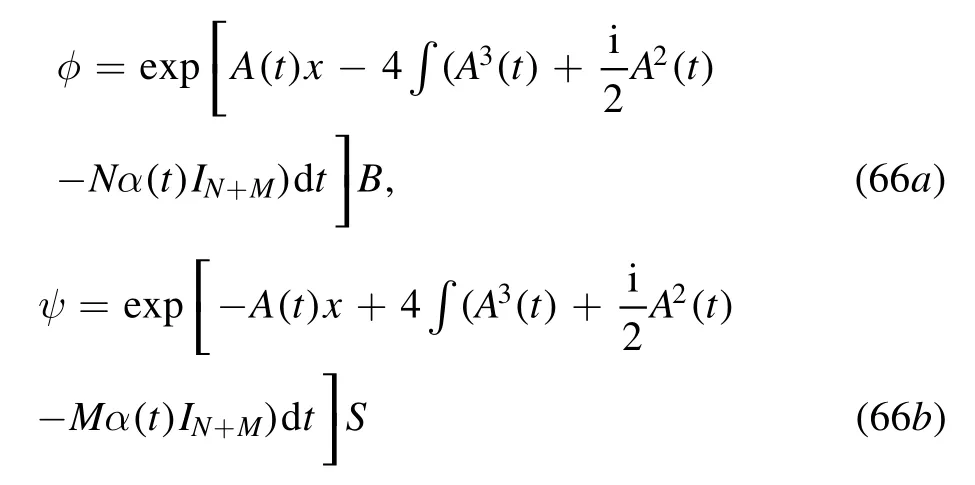
for meeting (62) and (64)，where At(t)=α(t)A(t)，α(t) is real，A(t) and ∫Aj(t)dt commute for j=2，3，and B，S are column vectors inCN+M.

The proof can be implemented via a standard procedure of Wronskian verifications.This will be given in appendix.

3.2.2.Reduction of solutions.After getting the solutions to the unreduced systems (20) and (23)，in order to obtain solutions to the reduced equations (5) and (6) based on the reduction r=-q*，let us introduce the conditions imposed on A，φ and ψ.For this sake，we take M=N in theorem 2 and consider block matrices

whereK=K(t) ∈CN×N[t] commutes with ∫Kj(t)dt for j=2，3.Note that such A and T satisfy

Then，for those φ and ψ given in theorem 2，requiring S=TB，one can easily find

And further，making use of the relation(68)and the procedure of reductions on double Wronskians developed in [32，33]，for the double Wronskians f，g，h defined in theorem 2，we have

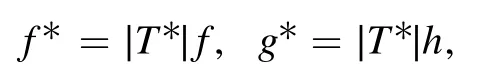
which yields q=-r*=g/f.Thus，we arrive at the following.

Theorem 3.The nonisospectral equations (5) and (6) have the following solution

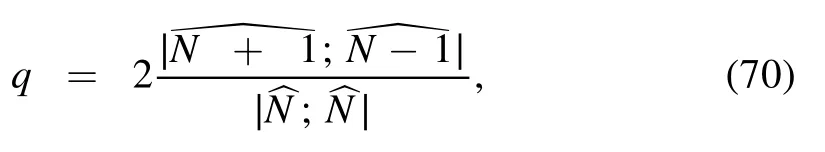
where the entry vector φ is given as

where

for equation (5)，and

for equation (6)，whereK=K(t)，∫K j(t)dtand their complex conjugates commute，respectively，for j=2，3 andB±are column vectors in CN.ψ is defined through (69).

Note that when M=N the part ∫(Nα(t)IN+M)dt and∫(Mα(t)IN+M)dt in(65)and(66)do not contribute to q and we therefore omit them in (72) and (73).

In the following step，we give explicit form of φ with respect to the nature of K.

Case 1:Let K be in the form

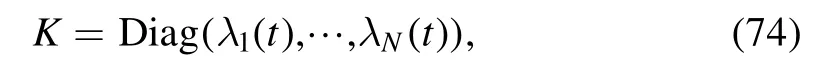
whereλj(t) =cjκ(t)，cj∈C，j=1，…，N，for κ being a specific function of t.In this case，φ takes the form (71)，where for the nonisospetral mKdV equation (5)，

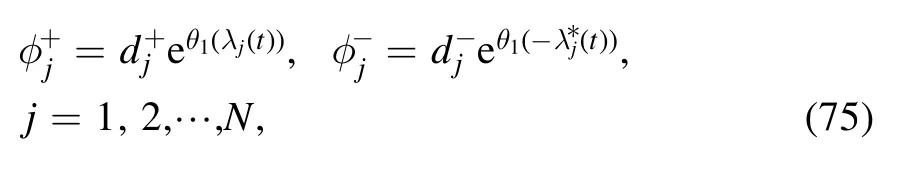
and for the nonisospetral Hirota equation (6)，

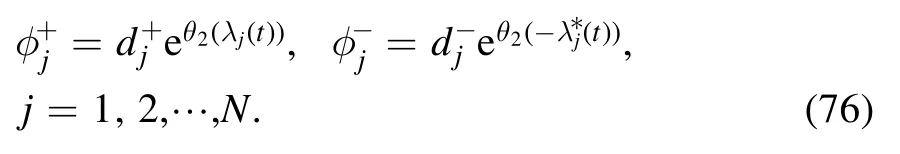
Hered±∈ Cand

Case 2:Letting K be a Jordan matrix as follows

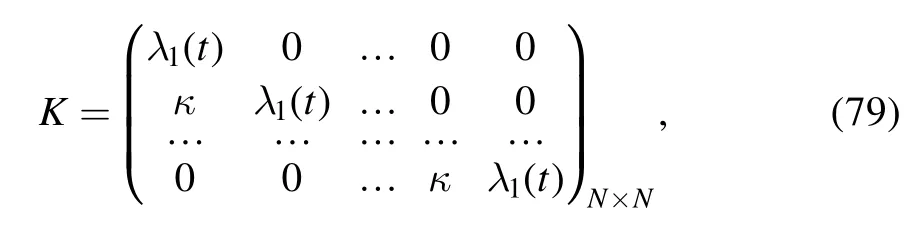
where λ1(t)=c1κ(t).In this case，we have

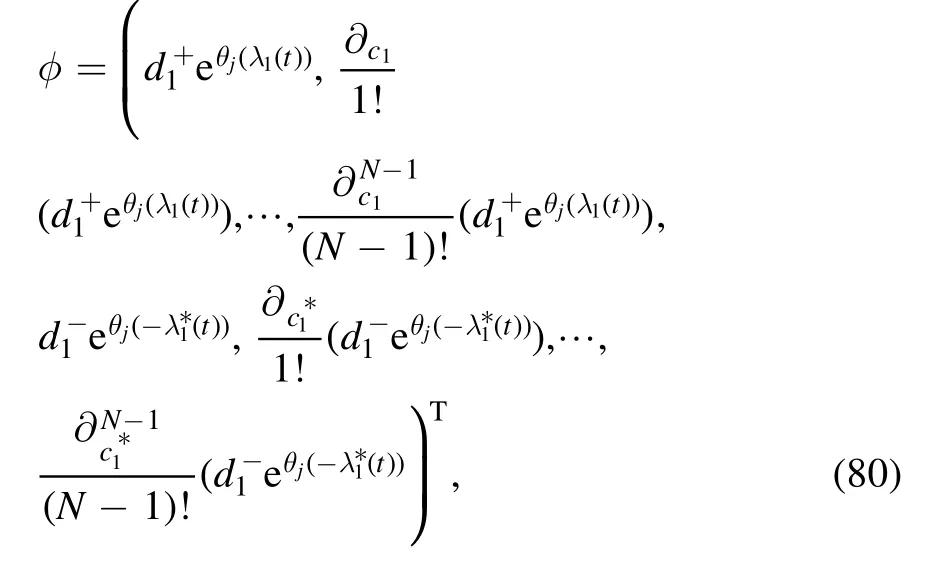
where j=1 for the nonisospetral mKdV equation (5) and j=2 for the nonisospetral Hirota equation (6).

3.2.3.Dynamics.In this part，we take

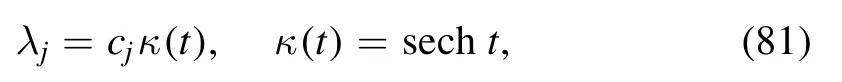
as an example，and from now on we takecj=aj+ibj，a j，bj∈R，and=1for convenience.Corresponding 1-soliton solutions are

for equation (5)，and

for equation (6).Different from the nonisosprctral KdV equation (4) where the dynamics of the soliton solution is controlled by one parameter cj，here for the nonisospectral complex mKdV equation (5) and the Hirota equation (6)，dynamics of solutions are controlled by two independent parameters: ajfor the governance of the amplitude，and aj，bjtogether governing the velocity.Results about 1-soliton solutions to equations (5) and (6) are shown in figure 6.

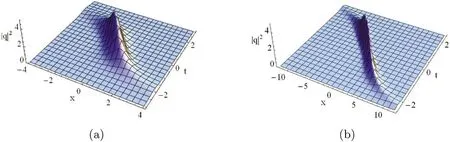
Figure 6.Shape and motion of 1-soliton solution to equations(5)and(6):(a)1-soliton given by(82)for c1=1+0.5i;(b)1-soliton given by(83) for c1=-1-i.

In order to show the interaction of two solitons of the equations (5) and (6)，we take N=2 in (70)，the 2-soliton solution

corresponding to

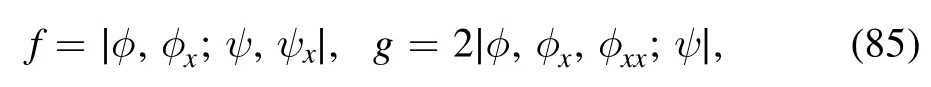
with

where θj(λ(t))，(j=1，2)are given as(77)and(78)，and j=1 for equation (5) and j=2 for equation (6)，respectively.Interpretation of the resulted solutions is given in figure 7.

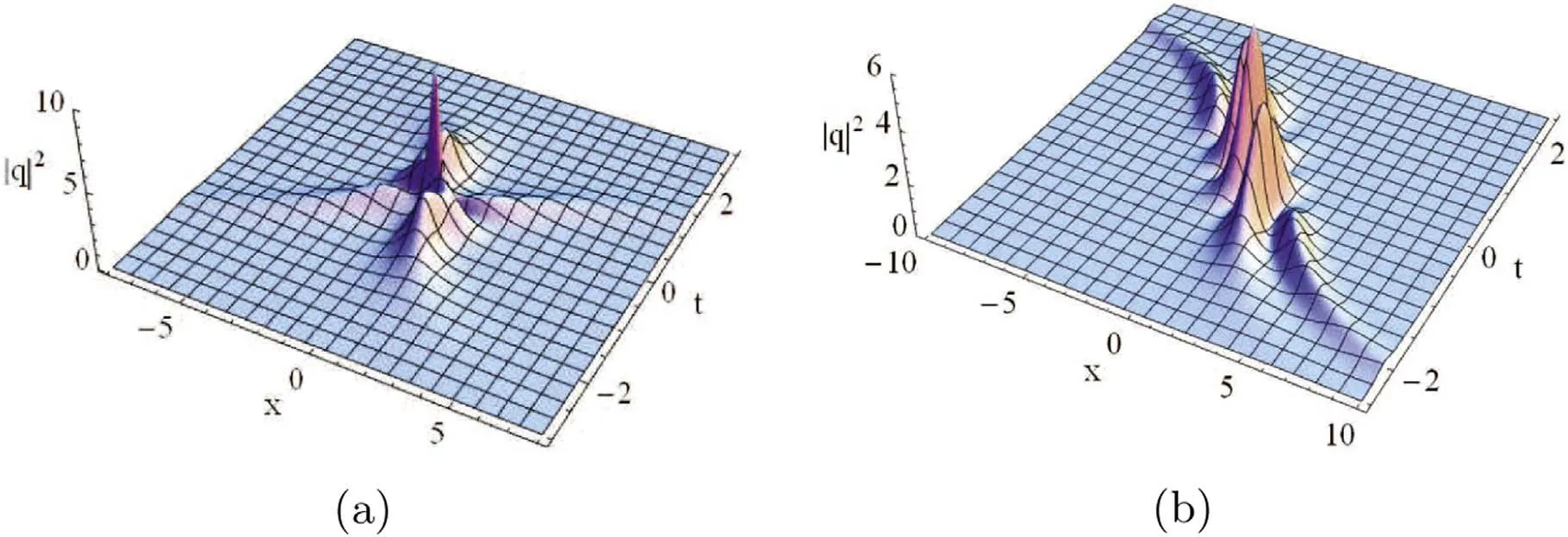
Figure 7.Two solitons interactions of equations(5)and(6)，given by(84)with(85)and(86):(a)collisions of two solitons to equation(5)forb) periodic interactions of two solitons to equation (6) for c1=0.5-0.6i，c2=0.7+0.6i.

We sum up with the limit solutions to equations (5) and(6).The simplest limit solution corresponds to taking φ defined as

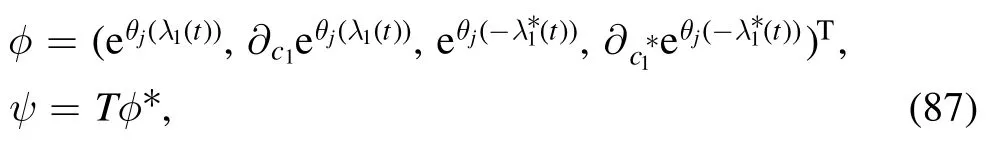
where θj(λ(t))，(j=1，2)are given as(77)and(78)，and j=1 for equation (5) and j=2 for equation (6)，respectively.Figure 8 depicts the behaviour of these limit solutions.

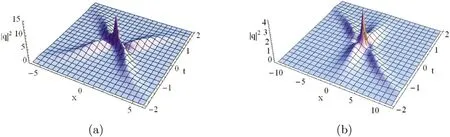
Figure 8.Shape and motion of limit solutions to equations(5)and(6)，given by(84)with(85)and(87):(a)envelope of the limit solution to equation (5) for0.5i;(b) envelope of the limit solution to equation (6) for c1=0.5-0.6i.

4.Conclusion

In this paper we have interpreted how space-time localized waves are generated by introducing nonisospectral effects.This idea is based on the fact that in isospectral case amplitude of a soliton is usually governed by the spectral parameter and then introducing a time-dependent spectral parameter may generate a localized amplitude with respect to time.Such a nonisospectral deformation leads to integrable systems as well.We have employed three equations，i.e.the nKdV equation (4)，the nonisospectral complex mKdV equation (20) and the nonisospectral Hirota equation (23) as examples，and derived their solutions in terms of Wronskians and double Wronskians.Since these equations are integrable，other approaches，such as the inverse scattering transform[34] and Cauchy matrix approach [35–38] can also be employed to get their solutions.Note that the later two equations belong to the ZS-AKNS hierarchy and we derived their solutions from those of unreduced systems(20)and(23)by means of recently developed reduction technique[32，33]，which has been demonstrated effective in practice in getting solutions of the reduced equations involved complex reductions (e.g.[22，39–42]).In this paper，such a reduction technique is shown to be useful in nonisospectral case as well.

Finally，as we have remarked in the first section，although these nonisospectral equations can be gauge-transformed to their isospectral counterparts，the investigation is still meaningful，as we have interpreted a mechanism to generate spacetime localized solitary waves by introducing nonisospectral effects which are usually related to non-uniformity of media，and this is also potentially useful in some physics models such as the NLS equation with an external potential (the GP equation) and some circumstance to generate rogue waves.Such a mechanism is efficient for extension to other integrable systems.

Acknowledgments

This project is supported by the National Natural Science Foundation of China (Nos.11875040 and 11 571 225).

Appendix.Proof of theorem 2

We sketch hints to the proof of the theorem by taking the bilinear form (60) as an example.Direct computations of the different x-derivatives yield

In addition，it is easy to find according to equation (64) that

Thus，the t-derivatives are

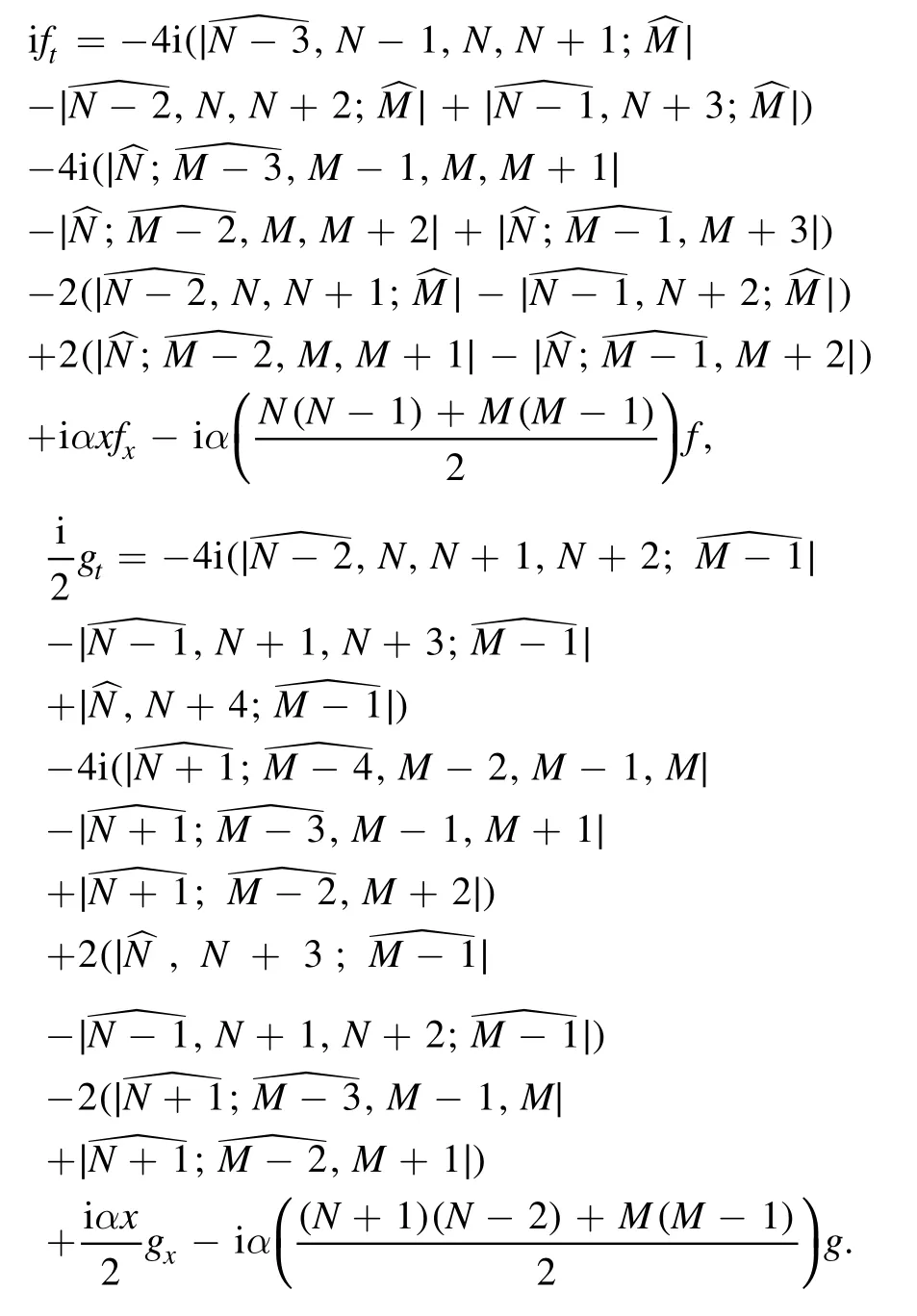
Similarly，we can obtain the derivatives of h.

Let us also recall the following determinantal identity[27]

where K is an arbitrary s×(s-2) matrix，and a，b，c and d are s-order column vectors，and the lemma below.

Lemma 1.[20，23] Suppose that Ξ = (ajs)M×Mis an M×M matrix with column vector set{βj} and row vector set{γj}.A = (Λjs)M×Mis an M×M operator matrix where each Λjsis an operator.Then we have

By this lemma one can generate identities used in Wronskian verifications.Takingand for 1 ≤j ≤N+M，

one has from lemma 1 that

whereTr(A)is the trace of A.Same computations can be done also for

In light of lemma 1，fromf[T r(A) (T r (A)f)] =(T r(A)f)2，it follows that

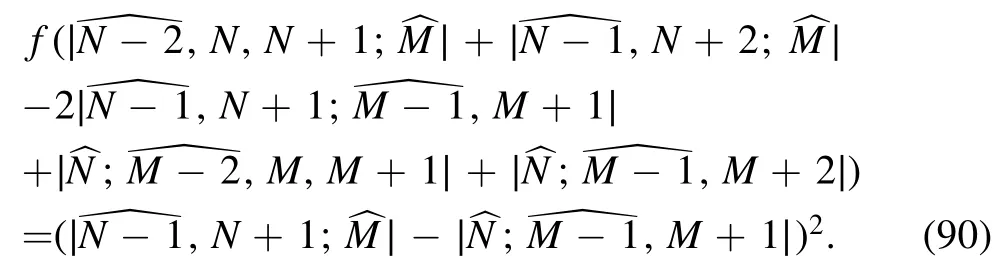
Moreover，from the relations

we can，respectively，obtain

and

One more result is that

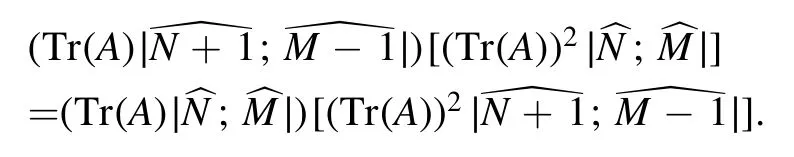
Under these circumstances，one can substitute those derivatives into (60a) and make use of the above identities to simplify expressions，and then arrives at

which can be proved null by virtue of the identity(88).Thus，(60a) is valid.Similar procedure can be done to prove (60b)and (60c).