Magnetic impact on heat and mass transfer utilizing nonofluid in an annulus between a superellipse obstacle and a cavity with periodic side-wall temperature and concentration

Abdelraheem M Alyand Noura Alsedais

1 Department of Mathematics，King Khalid University，Abha 62529，Saudi Arabia

2 Department of Mathematics，Faculty of Science，South Valley University，Qena 83523，Egypt

3Department of Mathematical Sciences，College of Science，Princess Nourah Bint Abdulrahman University，Riyadh，Saudi Arabia

Abstract The magnetic impacts upon the transport of heat and mass of an electrically conducting nanofluid within an annulus among an inner rhombus with convex and outer cavity with periodic temperature/concentration profiles on its left wall are assessed by the ISPH method.The right wall has Tc andCc ，flat walls are adiabatic，and the temperature and concentration of the left wall are altered sinusoidally with time.The features of the heat and mass transfer and fluid flow through an annulus are assessed across a wide scale of Hartmann number Ha，Soret numberSr，oscillation amplitude A，Dufour number Du，nanoparticles parameterφ，oscillation frequency f，Rayleigh number Ra，and radius of a superellipsea at Lewis numberLe= 20，magnetic field’s angleγ = 45° ，Prandtl numberPr= 6.2，a superellipse coefficient n= 3 /2，and buoyancy parameter N= 1.The results reveal that the velocity’s maximum reduces by70.93% as Ha boosts from 0 to 50，and by 66.24%as coefficienta boosts from0.1 to0.4.Whilst the velocity’s maximum augments by 83.04% asSr increases from 0.6 to 2 plus a decrease in Du from 1 to 0.03.The oscillation amplitude A，and frequency f are significantly affecting the nanofluid speed，and heat and mass transfer inside an annulus.Increasing the parameters A and f is augmenting the values of mean Nusselt number Nu and mean Sherwood number Sh.Increasing the radius of a superellipsea enhances the values of and

Keywords: Dufour number，ISPH method，nanofluid，Soret number，rhombus，magnetic field

Nomenclature

Greek symbols

Subscripts

1.Introduction

The research of the magnetic impacts has received a lot of consideration in engineering due to its wide range of uses for instance polymer and metallurgical industries，where hydromagnetic practices are employed.Lo[1]studied the magnetic impacts on a buoyancy-driven flow in an enclosure.Oztop et al [2] investigated the MHD natural convection from two semi-circular heaters inside an enclosure.The magnetic field is employed in controlling heat and fluid flow.Knowledge of the magnetic influences on the heat transfer process and flow actions inside enclosures occupied by electrically conducting fluids has become increasingly important [3—10].Recently，fluid dynamics researchers have shown a strong interest in the development of natural/mixed convection in nanofluid-filled cavities owing to their applications in various disciplines.Sherement and Pop [11] utilized the Buongiorno model to examine the natural convection in a porous cavity occupied by a nanofluid.In a heated closed rectangular enclosure，Alina and Lorenzini[12]studied the thermal behavior of ZnO-water nanofluid.Using the Lattice Boltzmann Method，Nemati et al[13] and Zhou and Yan [14] investigated natural convection through MHD flow in a cavity.The magnetic field is found to minimize cavity circulation.Mehmood et al[15]examine the magnetic impacts and thermal radiation on mixed convection of a nanofluid in a square porous cavity.More studies can be found in [16—27].

There are a considerable number of studies that consider natural convection in different cavities including the inserted bodies.Natural convection caused by a hot inner circular cylinder inside a cold outer enclosure is calculated numerically by Kim et al[28].Sheikholeslami et al[29]investigated natural convection in a circular cavity including a sinusoidal cylinder.Jabbar et al[30]investigated natural convection in a sinusoidal enclosure having a circular cylinder.Aly [31]examined the double-diffusion in a porous enclosure contained nanofluid over two circular cylinders.Pop et al [32]studied the transmission of thermo-gravitational convection in a differentially heated chamber involving an adiabatic solid body.Sheremet et al [33] studied the thermo-gravitational of Al2O3—SiO2/H2O in a porous space holding a heat-conducting body.Bhattacharyya et al [34] examined heat and mass transport in a porous channel under the influences of Dufour，Soret，and inclined magnetic field.Kumar et al[35]explained the impacts of magnetite nanofluid over a rotating disk with considering chemical reaction and magnetic field.Shanker et al [36] checked partial velocity slip on MHD convective flow over a stretching surface.The topic of the nonuniform temperature profiles is occurring in several industrial applications，for instance，solar energy collection，building thermal isolations，energy storage，and cooling of electronic elements[37—42].

The periodic changes in the electronic components’current are providing time changes in their surface temperature.This paper treats the magnetic influences on the heat and mass transfer of an electrically conducting nanofluid inside an annulus.The regulating equations of the continuity，momentum，energy，and mass in the dimensionless form are solved by the ISPH method.The main outcomes after studying the impacts of the relevant parameters on the nanofluid flow and lineaments of the heat and mass transfer are:

· The increase in the Hartmann numberHa，nanoparticles parameterφ，and radius of a superellipseais slowing down the nanofluid speed in an annulus.

· The values ofandare augmenting as nanoparticles parameterφ，Rayleigh numberRa，amplitudeA，and frequencyfare increasing.

· IncreasingSrwith minimizingDuis improving the strength of the concentration distributions in an annulus，and accordinglyis strongly decreasing.

2.Mathematical analysis

Figure 1 describes the preliminary geometry and its particles model.In an outer cavity，the horizontal walls are presumed to be adiabatic，right wall is held atTcandCc，and the left wall is altered with sinusoidal temperature/concentration in a time.

Figure 1.Geometry of the problem.

The equation of the superellipse is:

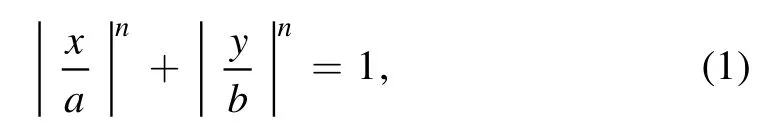
wheren，aandbare positive numbers，and their values are taken asn= 3 /2，anda=bis varied throughout the computations.Hence，the superellipse shape is taken as a rhombus with convex corners.The flow assumptions are:

· The Boussinesq approximation is utilized，in which density variations are ignored except via the gravity term.

· The inclined magnetic field (B0) used with an incline angleγalongx-yaxis with ignoring the viscous dissipation and Joule heating impacts.

· One phase model is employed for nanofluid modeling.

· The fluid flow is laminar，incompressible，and transitional.

The governing equations are [43，44]:

The dimensionless quantities:

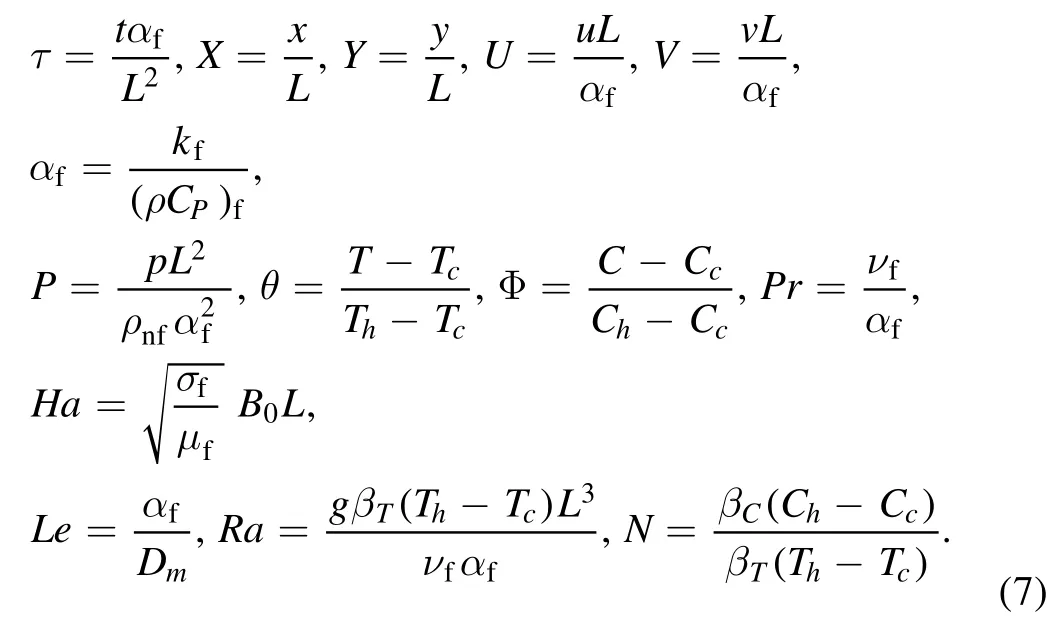
After substitute equation(7)in(2)—(6)，the dimensionless equations are:

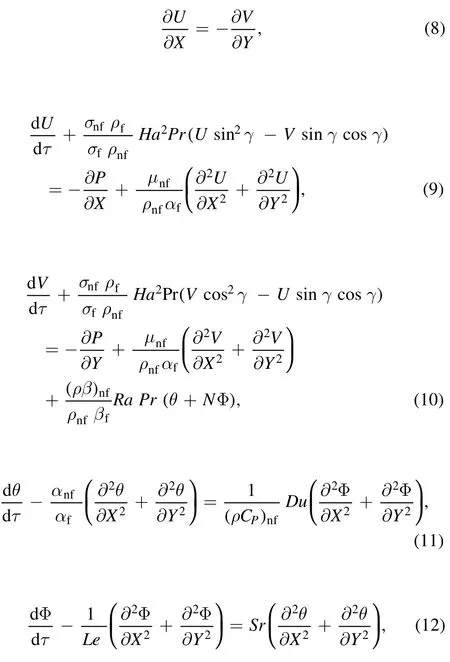
2.1.Dimensionless boundary conditions

Cavity’s right‐wall，and an inner blockageU=0，

V= 0，θ= 0 = Φ，

Mean Sherwood number:

Mean Nusselt number:

2.2.Nanofluid thermophysical properties

In this study，the water is a base fluid and copper (Cu) is the nanoparticles.The physical attributes of the copper and H2O are shown in table 1.

The density，specific heat，and thermal conductivity of a nanofluid [47—50]，are:

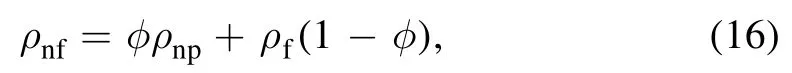
Table 1.Physical attributes of copper (Cu) and H2O [45，46].

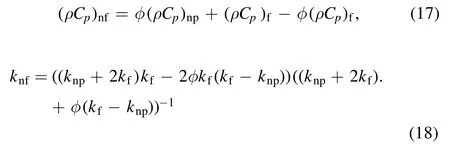
The Brinkman model for effective dynamic viscosity of a nanofluid [51]:

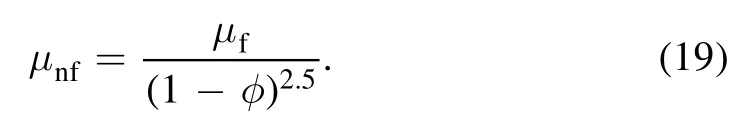
Electrical conductivity of a nanofluid:

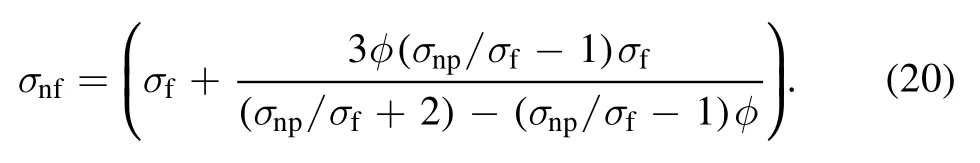
3.ISPH formulation

The ISPH method employs a quintic kernel functionW:

whereq=rij/h.The description off(ri) in SPH estimation:

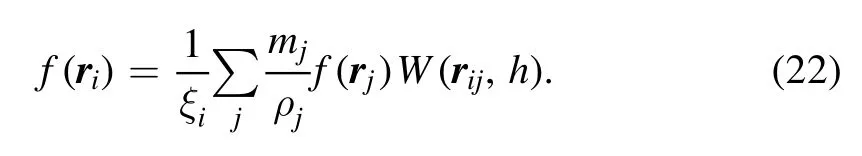
The renormalization factorξi[43，44，52] is:

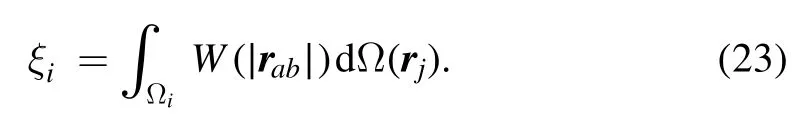
The first derivative is:

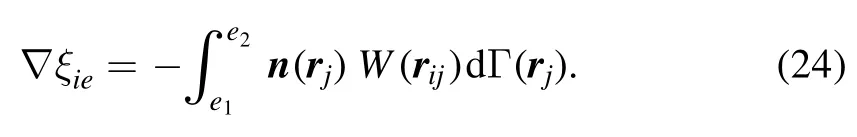
3.1.Solving steps

The projection method [53] is employed in the ISPH method as:

The projected velocities are:

Pressure Poisson equation:

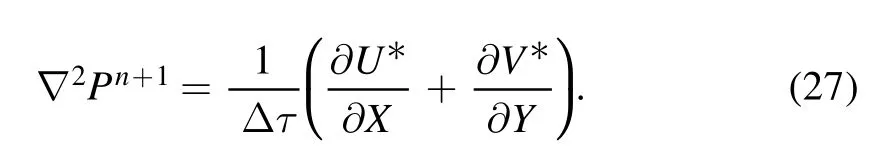
The updated velocities are:

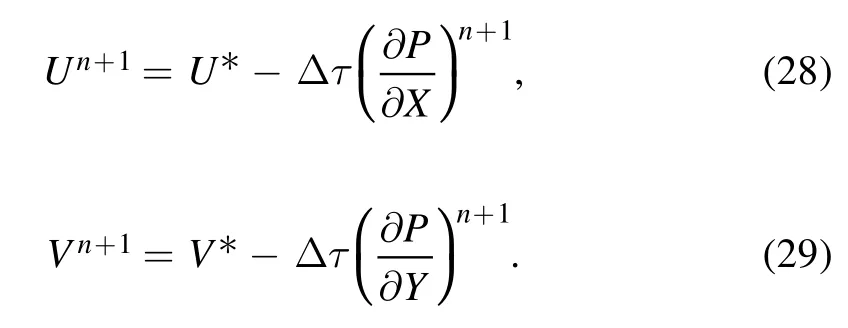
The thermal and concentration equations are:

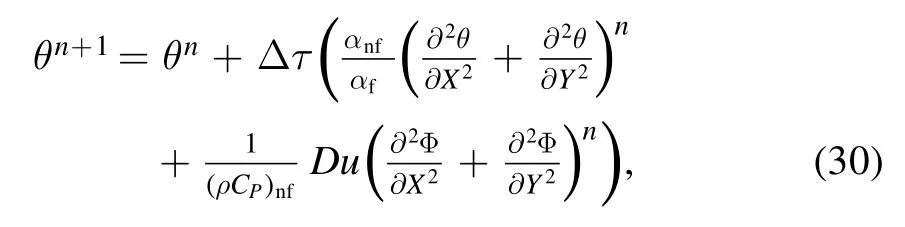
The positions are:

The shifting technique is:

3.2.Validation of the ISPH method

The comparison between numerical and experimental results from Paroncini and Corvaro [54] and the ISPH results are introduced in figure 2.The comparison showed the agreement of the ISPH results compared to the experimental and numerical results [54].Further，there are numerous validation examinations during the earlier studies of the ISPH method[43，44，52，55].

Figure 2.Isotherms of the numerical and experimental results of [54] and the ISPH results.

4.Results and discussion

Results are processed for a large scale of parameters.The frequency and amplitude of the temperature/concentration are varied over(5≤f≤100) and (0.5 ≤A≤2) ，respectively.Hartmann number，nanoparticles parameter，Soret number，Rayleigh number，Dufour number，and radius of a superellipseaare varied as (0 ≤Ha≤50) ，(0≤φ≤0.05)，(0.6 ≤Sr≤2)，(103≤Ra≤105)，(0.03 ≤Du≤1) ，and(0.03 ≤a≤1) ，respectively.All over the computations，buoyancy parameter isN=1，magnetic field’s angle isγ= 45° ，Lewis numberLe=20，a superellipse coefficientn=3 / 2，and Prandtl numberPr=6.2.

Figure 3 shows the influences of nanoparticle’s parameterφon a nanofluid velocity，and deployments of temperature and concentration in an annulus atγ= 45° ，N=1，n=3 /2，a=0.35，Ra=104，A= 0.5，f=5，Sr=1，Du=0.12，andHa=10.For addition of the nanoparticles，the first remark is a decline in the velocity’s maximum by 17.49% asφgets from 0 until 0.05.Physically，adding nanoparticles serves an extra effective viscosity of a nanofluid.The second remark is that an extra value ofφdeclines the temperature and enhances the concentration within an annulus between a cavity and an inner superellipse.Figure 4 shows the reliance ofandon the time and nanoparticle’s parameters atγ= 45° ，N=1，n= 3 /2，a=0.35，Ra=104，A= 0.5，f=5，Sr= 1，Du=0.12，andHa=10.It is noted that a significant enhancement is existing in the values ofandfor higher nanoparticle’s parameterφ.

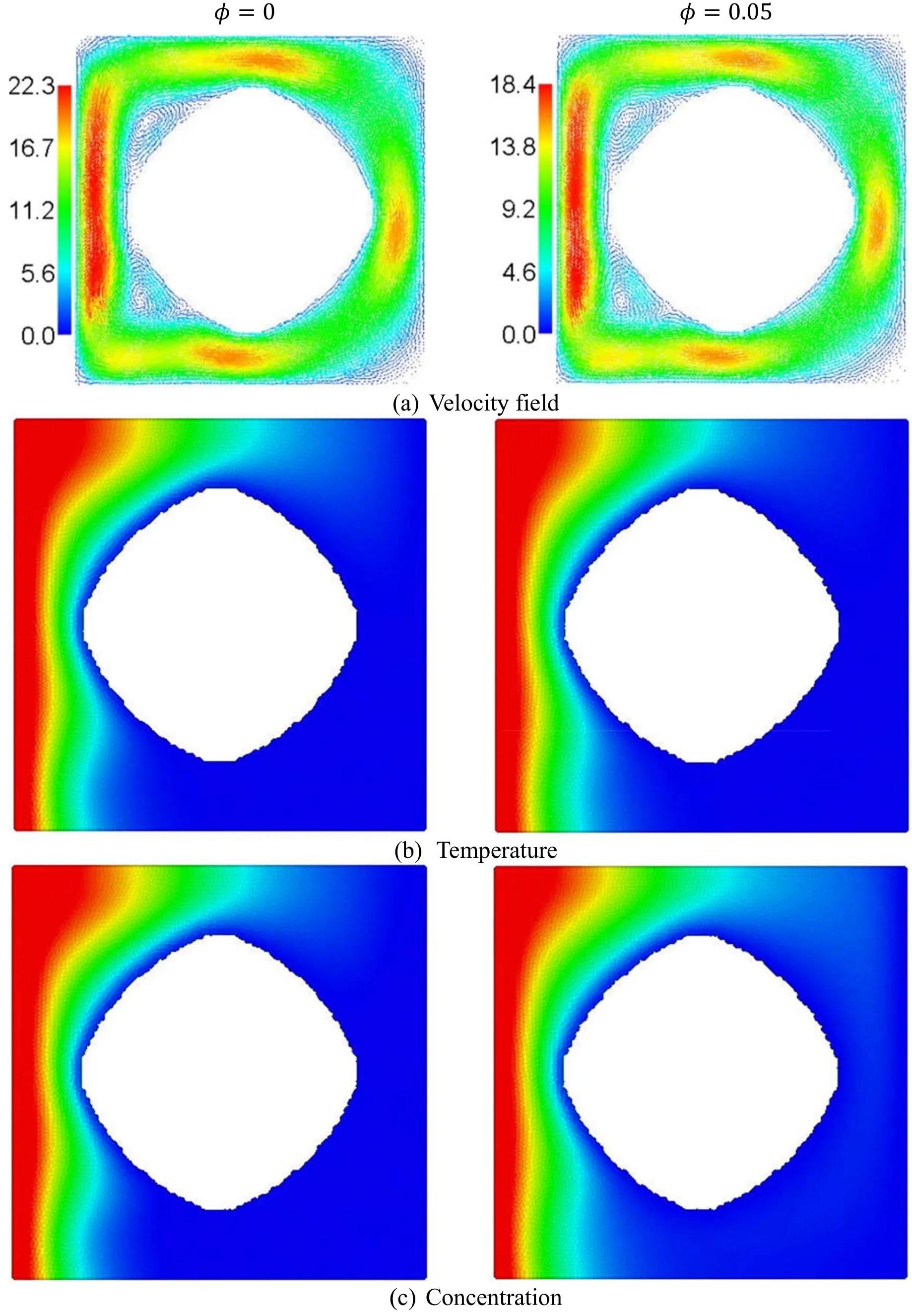
Figure 3.The influences of nanoparticle’s parameterφ on nanofluid velocity，and deployments of temperature and concentration at γ = 45° ，N = 1，n =3 /2，a = 0.35，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andHa =10.

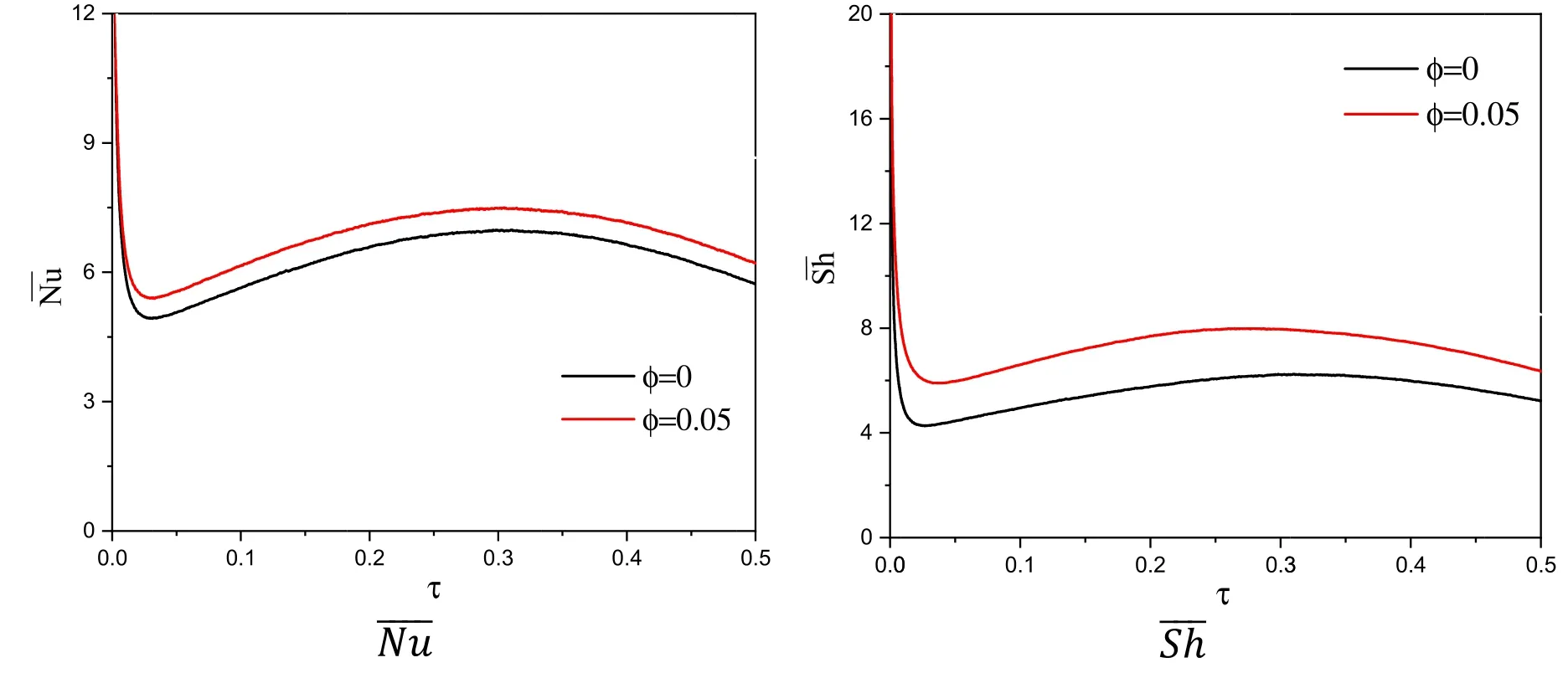
Figure 4.The values of and below the influences of the nanoparticle’s parameter at γ = 45° ，N = 1，n =3 /2，a = 0.35，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andHa =10.

The sequences of the velocity，temperature，and concentration contours are plotted at various Hartmann numberHaatγ= 45° ，N= 1，n=3 /2，a= 0.35，Ra=104，A= 0.5，f=5，Sr= 1，Du=0.12，andφ= 0.06 are shown in figure 5.Physically，the extra Lorentz forces of a magnetic field are produced at a higher Hartmann number.As a result，the velocity’s maximum reduces by 70.93%according to an increase inHafrom 0 to 50.In figures 5(b)—(c)，there is a little reduction in the temperature and concentration contours within an annulus as the Hartmann number increases.Further，figure 6 presents the dependence ofandon the Hartmann number atγ= 45° ，N= 1，n=3 /2，a= 0.35，Ra=104，A=0.5，f=5，Sr= 1，Du=0.12，andφ= 0.06.It is clear that an increment on the Hartmann number reduces the values ofandwhich highlighting the Lorentz forces’controls on the convection flow.

Figure 5.The influences of the Hartmann number on nanofluid velocity，and deployments of temperature and concentration at γ = 45° ，N=1，n = 3 /2，a =0.35，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

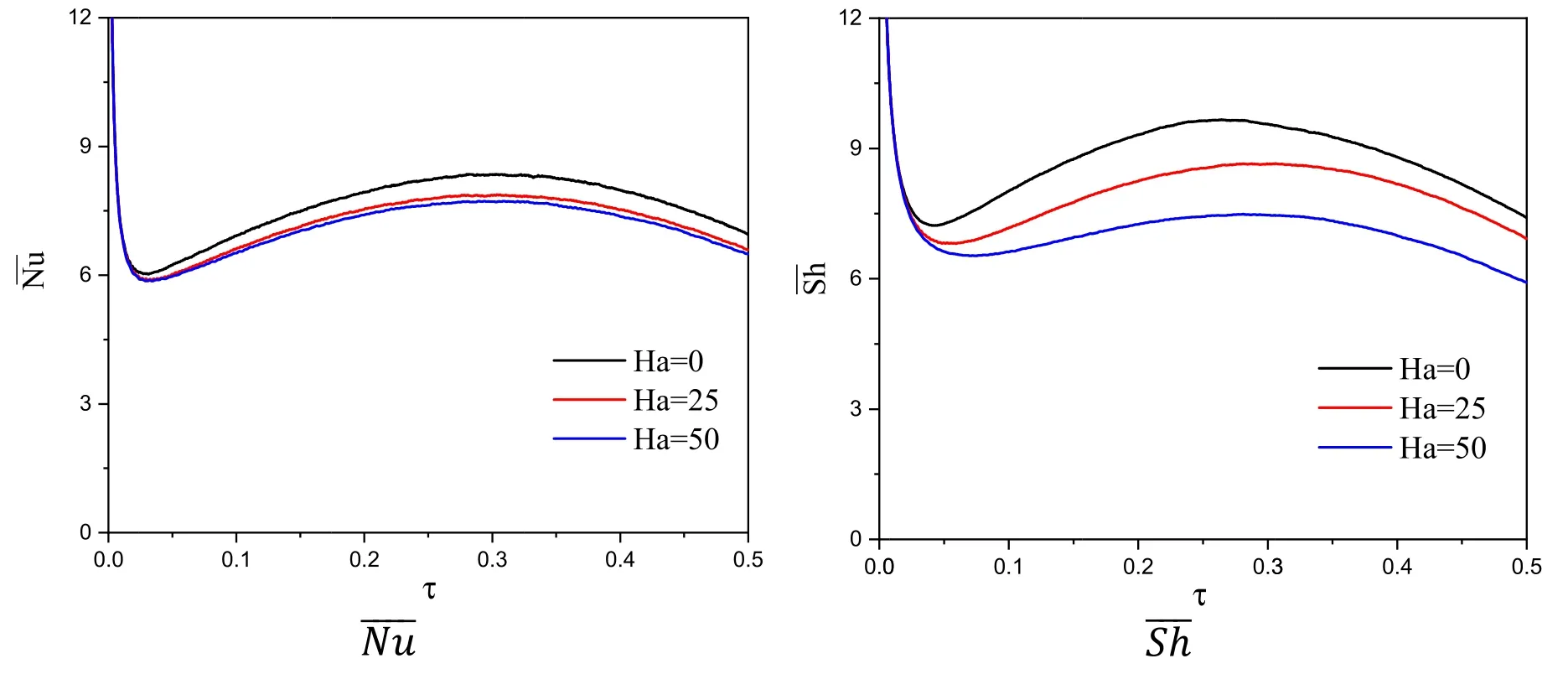
Figure 6.The values of and below the influences of the Hartmann number at γ = 45° ，N = 1，n =3 /2，a = 0.35，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

Figure 7.The influences of coefficient a for a superellipse on nanofluid velocity，and deployments of temperature and concentration at γ = 45° ，N = 1，n =3 /2，Ha = 10，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

Figure 7 introduces the impacts of a superellipse radiusaon the nanofluid velocity，and deployments of temperature and concentration in an annulus atγ= 45° ，N=1，n=3 /2，Ha= 10，Ra=104，A= 0.5，f=5，Sr=1，Du=0.12，andφ= 0.06.As the lengthacontrols the radius of an inner superellipse-blockage，an increment inafrom0.1 to0.4，the velocity’s maximum lessens by 66.24% and the temperature and concentration contours are reducing within an annulus.Physically，the inner superellipse represents a blockage for the convection flow，and consequently，as the area of a superellipse increase by an increment ina，the nanofluid movement and the deployments of the temperature and concentration are shrinking within the area between a cavity and an inner blockage.The impacts of the radius of a superellipseaon the values ofandare shown in figure 8.It is noted that an expansion in the radiusaaugments the values ofand.

Figure 8.The values of and below the influences of the radius of a superellipse a at γ = 45° ，N = 1，n =3 /2，Ha = 10，Ra =10 4，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

Figures 9 and 10 show the impacts of combination values of the Soret—Dufour parameters(Sr and Du)on the nanofluid velocity，and deployments of temperature and concentration in an annulus as well asandatγ= 45° ，N=1，n= 3 /2，a=0.35，Ha= 10，Ra=104，A= 0.5，f=5，andφ= 0.06.In figure 9(a)，the velocity’s maximum increases by 83.04% asSrincreases from 0.6 to 2 with a decrease inDufrom 1 to 0.03.In figures 9(b)—(c)，according to an increase inSr(or a decrease inDu)，there are slight changes in the temperature and a clear decrease in the concentration within an annulus.In figure 10，is slightly enhanced andis strongly decreased asSrincreases with a decrease inDu.Physically，Soret number is a mass alter of a temperature difference and Dufour number is a heat alter from the concentration difference.The combinations ofSrandDucan be found are referred in [31，56，57].

Figure 9.The influences of the Soret and Dufour parameters on nanofluid velocity，and deployments of temperature and concentration at γ = 45° ，N = 1，n =3 /2，a = 0.35，Ha =10，Ra = 10 4，A = 0.5，f =5，andφ = 0.06.

Figure 10.The values of and below the influences of Soret and Dufour numbers at γ = 45° ，N=1，n =3 /2，a = 0.35，Ha =10，Ra =10 4，A = 0.5，f =5，andφ = 0.06.

Figures 11 and 12 show the influences of the Rayleigh numberRaon the nanofluid velocity，and deployments of temperature and concentration in an annulus as well asandatγ= 45° ，N= 1，n=3 /2，a= 0.35，Ha=10，A= 0.5，f=5，Sr= 1，Du=0.12，andφ= 0.06.In figure 11，asRapowers，the intensity of the velocity field boosts clearly and the temperature and concentration are improved from almost straight lines to the parallel lines across an annulus over a superellipse blockage.In figure 12，an increment inRaprovides a clear increment in the values ofand.Physically，increasingRapowers the buoyancy force which accelerates the nanofluid movements and enhances the heat/mass transport within an annulus.

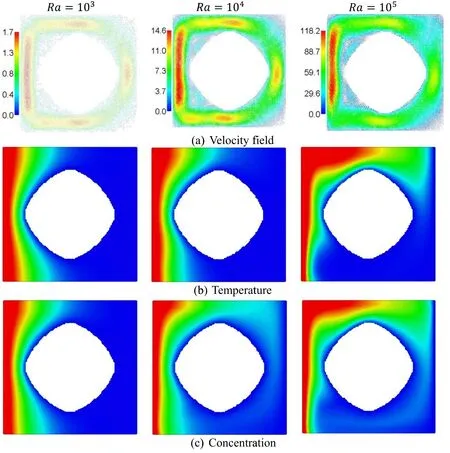
Figure 11.The influences of Ra on nanofluid velocity，and deployments of temperature and concentration at γ = 45° ，N=1，n = 3 /2，a =0.35，Ha =10，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

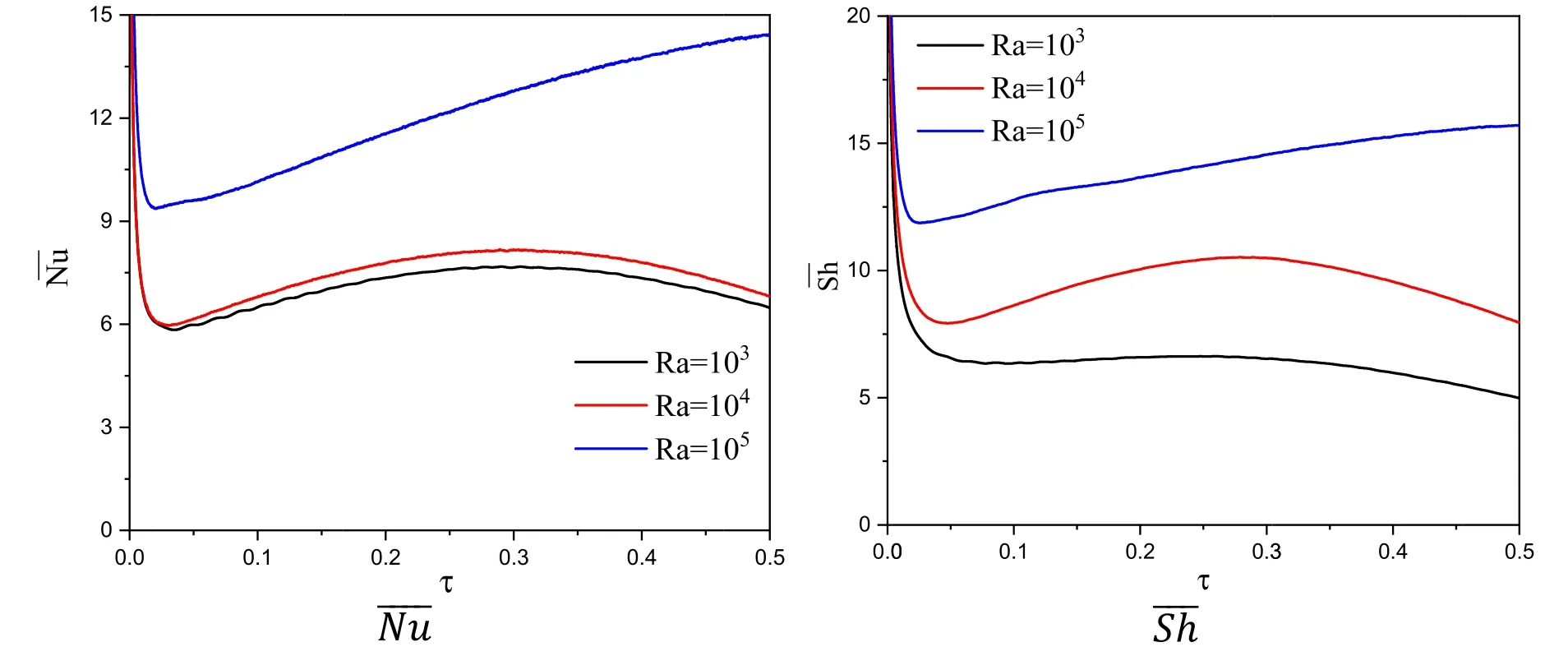
Figure 12.The values of and below the influences of the Ra at γ = 45° ，N=1，n = 3 /2，a =0.35，Ha =10，A = 0.5，f =5，Sr = 1，Du =0.12，andφ = 0.06.

Figures 13—15 present the influences of the amplitudeAand frequencyfof the temperature and concentration oscillation on the nanofluid velocity，temperature and concentration within an annulus atγ= 45° ，N= 1，n=3 /2，a=0.35，Ha=10，Ra=104，Sr= 1，Du=0.12，andφ=0.06.In figure 13，it is remarked that as an amplitudeAraises from 0.5 to 2，the velocity’s maximum increases by 66.23%atf=5，whilst it decreases by 42% atf=50，and by 68.18%atf=100.In figures 14 and 15，it is observed that atf=5，the intensity of the temperature and concentration within an annulus is boosting extremely asAincreases from 0.5 to 2，whilst atf=50 or 100，the intensity of the temperature and concentration is decreasing asAincreases from 0.5 to 2.The fluctuations of the results are relevant to the definition of a sine wave for the periodic boundary condition of temperature and concentration in a left wall.Figure 16 shows a 3D-plot ofandbelow the influences of the amplitude and frequency of the temperature and concentration oscillation atγ= 45° ，N= 1，n=3 /2，a= 0.35，Ha=10，Ra=104，Sr=1，Du=0.12，andφ= 0.06.The values ofandare increasing as both of amplitudeAand frequencyfare increasing and it has seen whenf=50 andA=2，the highest values ofandare obtained.

Figure 13.The influences of the amplitude and frequency of the temperature and concentration oscillation on the velocity field at γ = 45° ，N=1，n = 3 /2，a =0.35，Ha =10，Ra =10 4，Sr = 1，Du =0.12，andφ = 0.06.

Figure 14.The influences of the amplitude and frequency of the temperature and concentration oscillation on the temperature at γ = 45° ，N = 1，n = 3 /2，a = 0.35，Ha =10，Ra = 10 4，Sr = 1，Du =0.12，andφ = 0.06.

Figure 15.The influences of the amplitude and frequency of the temperature and concentration oscillation on the concentration at γ = 45° ，N = 1，n =3 /2，a = 0.35，Ha =10，Ra =10 4，Sr = 1，Du =0.12，andφ = 0.06.

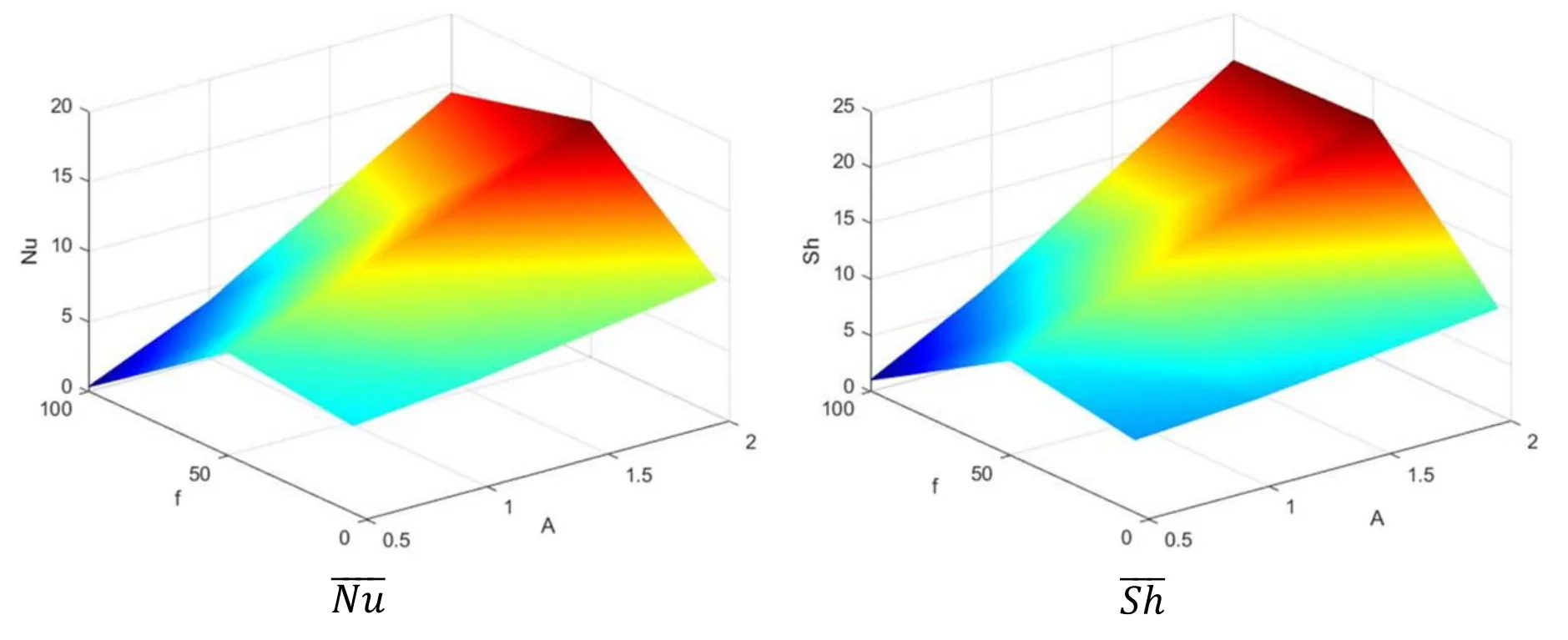
Figure 16.3D-plot of and below the influences of the amplitude and frequency of the temperature and concentration oscillation at γ = 45° ，N=1，n = 3 /2，a =0.35，Ha =10，Ra =10 4，Sr = 1，Du =0.12，andφ = 0.06.

5.Conclusion

The transport of heat and mass of an oscillating concentration and temperature in the left-side of an annulus between an inner rhombus with convex corners and an outer cavity is numerically investigated.The annulus is occupied by a nanofluid and is influenced by a magnetic field，thermo-diffusion，and diffusion-thermo.The implications of the pertinent parameters like oscillation amplitude，oscillation frequency，Hartmann number，nanoparticles parameter，Soret number，Rayleigh number，Dufour number，and radius of a superellipseaon the nanofluid flow and features of the heat and mass transmission have been discussed.It is remarked that the velocity’s maximum reduces by70.93%asHaraises from 0 to 50，by 66.24% as a radius of a superellipseaexpands from0.1 to0.4.AsAraises from 0.5 to 2，the velocity’s maximum declines by42% atf= 50，and by 68.18%atf= 100.Whilst the velocity’s maximum boosts by 66.23%atf= 5 asAincreases from 0.5 to 2，and by 83.04%asSrboosts from 0.6 to 2 with a decrease inDufrom 1 to 0.03.As an oscillation amplitudeAincreases from 0.5 to 2，the strength of the temperature and concentration is extremely boosting at an oscillation frequencyf=5，and decreasing atf=50 or 100.The values ofandare increasing as amplitudeAand frequencyfare increasing.The highest values ofandare obtained atf=50 andA=2.BoostingSrwith lower inDu，leads to the followings: the temperature distributions have little changes，the strength of the concentration distributions is augmented，is slightly enhanced，andis strongly decreased.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University，Abha，Saudi Arabia，for funding this work through the Research Group Project under Grant Number(RGP.2/144/42).This research was funded by the Deanship of Scientific Research at Princess Nourah Bint Abdulrahman University through the Fast-track Research Funding Program.

ORCID iDs