顾及冲突分析的模糊积分非监督变化检测

邵 攀 任 东 董 婷

1.三峡大学计算机与信息学院 宜昌 443002 2.三峡大学湖北省农田环境监测工程技术研究中心 宜昌 443002

变化检测指通过分析同一地区不同时相遥感影像获取地表变化信息的过程,是遥感领域的重要研究方向[1-3],广泛应用于城市研究[4]、灾害评估[5-6]、国

防建设[7]等领域.一般地,可通过监督和非监督两种途径实现变化检测.非监督变化检测除原始遥感影像外,不需其他任何信息,有着广阔的应用前景.

本文关注最常用的基于“差异图(Difference image,DI)”的非监督变化检测.该方法首先对两期影像进行预处理,然后比较预处理后影像生成差异图,最后通过分析差异图提取变化信息.虽然国内外学者从不同的角度提出了众多的差异图变化检测技术,但不存在一种普适性的检测方法[8].同时由于受到异物同谱、同物异谱、类别混叠、噪声以及(用来生成差异图的)对比算子局限性等因素的影响,差异图变化检测的检测结果有时不够理想.

将多差异图进行集成,挖掘和融合不同差异图的优势,是提高差异图变化检测性能的有效途径,也是近年来遥感变化检测的研究热点之一[8-11].根据抽象程度一般可将数据融合技术划分为三个层次:数据级、特征级和决策级[9].现有的多差异图融合变化检测主要是基于数据级和决策级的.

数据级差异图融合变化检测通过提升差异图的质量来提高检测精度:首先将不同的差异图进行集成得到质量更优的融合差异图,然后通过分析融合图像获取变化信息.Gong 等[10]利用小波变换集成自然对数差值和邻域均值比差异图.Zheng 等[11]通过加权平均法融合差值和自然对数差值差异图.Jia 等[12]利用多尺度小波核融合差值和比值差异图.Zhuang 等[13]首先通过融合波谱值差异和波谱夹角构造混合特征矢量(Hybrid feature vector,HFV),再对HFV 求范数生成融合差异图.

决策级差异图融合变化检测通过集成不同差异图的检测结果来增强检测性能.Le Hegarat-Mascle等[8]和Luo 等[14]采用证据理论(Dempster-Shafer theory,DS)对不同差异图的检测结果进行融合.Zhang 等[15]借助DS 和支持向量机对不同尺度的差异图进行决策级融合.霍春雷等[16]使用投票法(Majority voting,MV)对多个尺度的检测结果进行融合.Du等[9]将决策级融合技术引入城市变化检测,调查分析DS、MV 和模糊积分(Fuzzy integral,FI)对差异图的融合效果.Nemmour 等[17]利用FI 对多个支持向量机的检测结果进行集成.Hao 等[18]提出一种融合阈值技术和聚类算法的变化检测技术框架.

所有上述融合变化检测均有其技术优势,能够实现信息的有效融合.但总的来讲,差异图融合变化检测的研究还处在初步阶段,理论和方法探讨还不够深入,有许多关键问题亟待解决.对FI 等决策级融合,急需解决的关键问题之一是信息冲突问题:不同信源可能得到相互冲突的判断结果,当信源判断结果冲突严重时,容易造成融合错误.信息冲突问题是影响融合效果的根本原因之一.

本文以FI 为基础,提出一种全自动的顾及冲突分析的融合变化检测方法.该方法首先选取典型的对比算子,生成信息互补的差异图集;然后利用顾及冲突分析的FI(Conflict analysis-based FI,CAFI)对差异图进行决策级融合.所提出的CAFI在集成不同信源优势的同时,尝试解决信息冲突问题.利用三组真实遥感数据进行变化检测实验,与多种相关先进检测技术进行对比,以客观评估CAFI的有效性和可靠性.

1 CAFI 变化检测

CAFI 变化检测包括两个主要步骤:1)生成信息互补的差异图集合;2)利用所提出的CAFI 模型对差异图进行决策级融合.

1.1 生成差异图集

本步的主要任务是生成两期遥感影像的差异图集.假设X1和X2是两幅同一地区不同时刻的多光谱遥感影像,且已经过配准和辐射校正等预处理.

遥感文献中存在众多的差异图生成算法,常用的算法包括差值法、比值法、变化矢量分析(Change vector analysis,CVA)、主成分分析(Principle component analysis,PCA)、波谱相关性映射(Spectral correlation mapper,SCM)、波谱角度映射(Spectral angle mapper,SAM)和波谱梯度差值法(Spectral gradient differencing,SGD)等[2,19-20].差值法和比值法主要针对单波段遥感影像,分别采用差值运算和比值运算生成两期影像的差异图.CVA 是对差值法在多波段情况下的扩展,利用欧氏距离生成两期影像的差异图.PCA 通过主成分分析生成差异图,能够去除数据相关性,减少数据冗余.上述差异图生成算法主要利用波谱曲线的波谱强度差异(波谱特征样本点间的位置变化)来生成差异图.与上述算法不同,SCM 和SAM利用波谱角度差异来生成两期影像的差异图[19];而SGD 通过波谱梯度描述波谱曲线的形状信息,并基于波谱曲线的形状差异生成两期影像差异图[20].

波谱曲线包括波谱强度、波谱角度和波谱形状(梯度)三方面的信息.对(地表)发生变化的像元,可能导致其波谱强度、波谱角度和波谱形状三个方面均发生较大变化,亦可能只有其中某些方面发生较大变化[13,20].基于此,两期影像波谱曲线的变化可划分为7 种类型(表1),其中,性质a 表示具有较大的波谱强度变化;性质b 表示具有较大的波谱角度变化;性质c 表示具有较大的波谱形状变化.若只考虑波谱强度变化,则只能检测出变化类型1,4,5和7;若只考虑波谱角度变化,则只能检测出变化类型2,4,6 和7;若只考虑波谱形状变化,则只能检测出变化类型3,5,6 和7.忽略其中任何一方面,都会造成7 种变化类型(表1)不能被全部检测.比如,若未考虑波谱形状变化信息,则变化类型3(此类别只有波谱形状发生较大变化)不能被检测.综上可知,通过综合考虑两期影像的波谱强度、波谱角度和波谱形状差异,可提供互补的差异图集.另外,计算两期影像波谱强度差异时,可采用代数运算法(以CVA 为代表),也可采用数据变换法(以PCA 为代表).代数运算法和变换法具有一定的互补性,可提供互补的波谱强度差异.

表1 波谱曲线的变化类型Table 1 The change categories of spectral curve

基于上述分析,本研究选取CVA、SCM、PCA和SGD 来生成两期影像X1和X2的差异图集SDI,并将其记作SDI= {CVA,SCM,PCA,SGD}.其中CVA和PCA 描述波谱强度差异,SCM 描述波谱角度差异,而SGD 描述波谱形状差异;CVA 和PCA分别利用代数运算法和变换法生成差异图,能够提供互补的波谱强度差异.

CVA、SCM 和SGD 的技术细节可参见文献[19-20].而对差异图PCA,本研究首先计算两期影像X2和X1的比值差异矢量RX=(|1-,其中表示影像Xl的第b波段,B表示波段总数;然后通过PCA 技术得到RX的各主成分;最后通过方差贡献率将RX的各主成分加权平均得到差异图PCA.得到差异图集SDI后,对每组差异图进行归一化操作,使其在[0,1]中取值.

1.2 CAFI 融合模型

如图1所示,所提出的CAFI 融合模型包括3个步骤:1)初步融合.利用杰卡德相似系数(Jaccard similarity coefficient,JSC)、模糊聚类和FI 对信源(差异图)集进行决策级融合,得到初步融合变化检测图;2)自适应分割.利用模糊集合的模糊度计算像元的信息冲突程度,将初步融合变化检测图划分为冲突严重和冲突较弱区域;3)重新分类.将冲突较弱像元的初步融合结果作为其最终的变化检测结果,利用地统计学知识对冲突严重像元重新分类.用符号w1和w2分别表示未变化类和变化类.

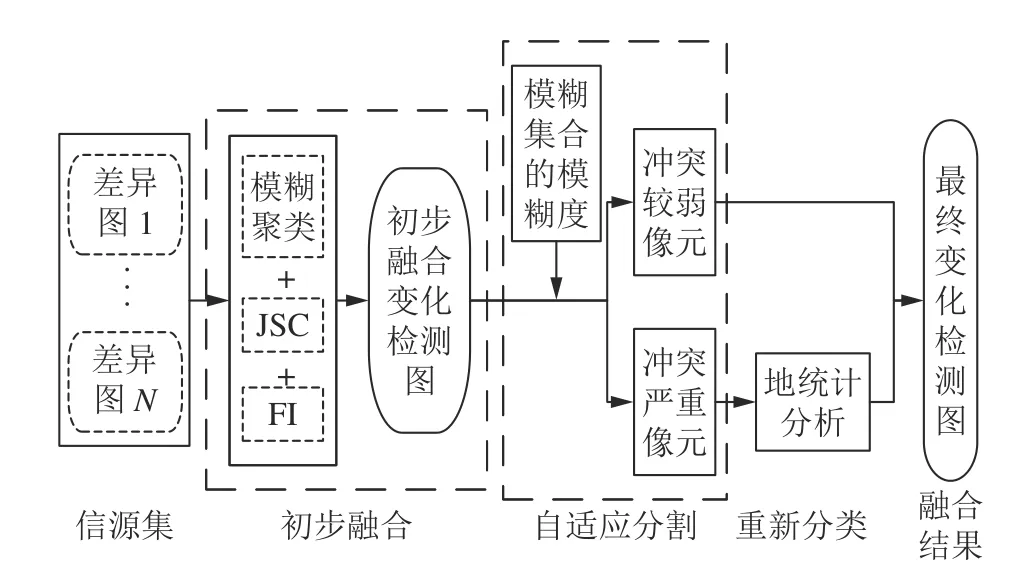
图1 所提出的CAFI 融合模型的基本流程Fig.1 Flowchart of the proposed CAFI fusion model

1.2.1 初步融合

模糊积分FI 是对传统积分的有效扩展,不要求信源相互独立,且能够同时考虑信源的重要程度和判断结果,为信息融合提供了一种强有力的工具[21].Sugeno 积分和Choquet 积分是两种最常用的模糊积分.所提出的CAFI 是一个融合技术框架,在初步融合步骤可采用不同的积分类型,本研究以Choquet 积分为例来研究和探讨CAFI.

Choquet 积分基于模糊测度对各信源的分类结果进行非线性合成.模糊测度用来表征信源的重要程度以及信源之间的相互作用.设集合Z={z1,z2,···,zN}是一个有限集合,用 2Z表示Z的幂集,称集合映射g:2Z →[0,1] 为一个模糊测度,若g满足:

1)g(Ø)=0 ;

2)g(Z)=1 ;

3)若A,B ∈2Z且A ⊆B,则g(A)≤g(B).

其中,Ø表示空集.利用Choquet 积分融合信息时,可采用不同的模糊测度,本文采用简单有效的gλ模糊测度[9].gλ模糊测度除满足上述3 个条件外,还满足以下性质:若A,B ∈2Z且A ∩B=Ø,则

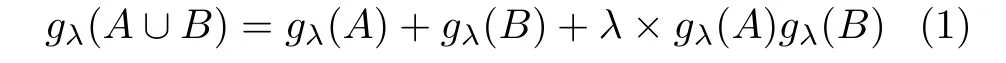
其中,λ ≥-1 .设h:Z →[0,1] 是集合Z上一个函数,且满足h(z1)≤h(z2)≤···≤h(zN),则基于gλ模糊测度的Choquet 积分可通过下式定义[21]

其中,h(z0)=0,An={z1,z2,···,zn},n=1,2,···,N,gλ(An)表示An的gλ模糊测度,可通过下式确定

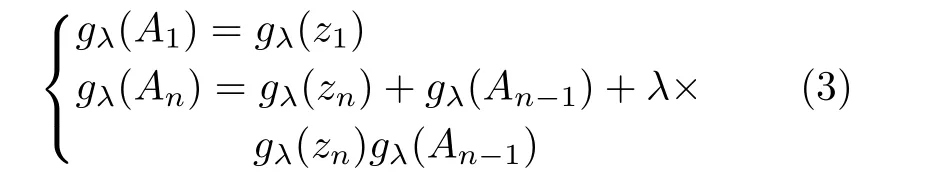
参数λ可通过解下面方程得到[9]

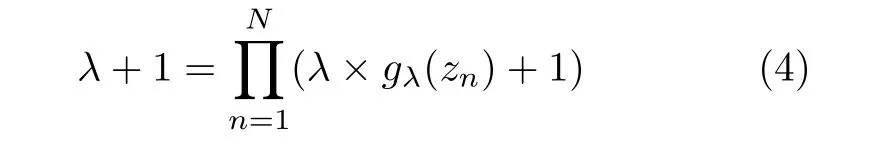
其中,gλ(zn)表示单元素集合{zn}的模糊测度.在用Choquet 积分进行信息融合时,集合Z表示信源集,信源zn的gλ模糊测度表示信源zn的重要程度,函数h(zn)表示信源zn的分类结果.本研究中信源集Z由N(N=4)组差异图构成(参见第1.1 节).

从上述分析可知,为通过Choquet 积分融合差异图集,需计算各差异图对像元的分类结果h(zn)和各差异图的gλ模糊测度(重要程度).如图2所示,基于Choquet 积分的初步融合步骤的基本流程包括:1)通过模糊聚类求解各差异图的分类结果(模糊分割矩阵);2)利用杰卡德相似系数JSC 估算差异图的gλ模糊测度;3)基于Choquet 积分融合差异图集,生成初步融合变化检测图.

图2 初步融合步骤的基本流程Fig.2 Flowchart of the preliminary fusion step

1)求解各差异图的分类结果

1.2.2 自适应分割

Choquet 积分能够实现多源信息的有效融合,然而当不同差异图的变化检测结果冲突严重时,可能导致融合错误.例如对某一像元,假设两组差异图将其分配给变化类,另外两组差异图将其分配给未变化类,信源之间冲突严重,很难判断其最终的检测结果,极易出现融合错误.信源冲突问题严重影响FI 的融合效果,为此,CAFI 对FI 得到的初步融合变化检测图进行进一步处理:识别初步融合变化检测图中的冲突严重像元并对其重新分类.

对任给像元pi,用符号ui(wk)表示基于信源(差异图)集Z,pi属于类别wk的所有隶属度的加权和,即

1.2.3 重新分类

对Non1∪Non2中像元,信源之间冲突较小,FI 能够得到较可靠的融合结果,故将其初步融合变化检测结果作为最终的检测结果:将Non1中像元标记为未变化类,Non2中像元标记为变化类;对Con1∪Con2中像元,信源之间冲突严重,需进行重新分类.

遥感影像的邻域像元间具有很强的相关性,且地表变化一般不是孤立的点,而是空间连通的区域[26].地统计学中的克里金插值理论通过观测值对未知点进行无偏、最优线性估计,能够很好地利用空间相关性,已被成功应用到众多领域.鉴于以上两点,本研究利用克里金插值技术对冲突严重像元重新分类.

任给冲突严重像元pi0,N(i0)为它的一个邻域,若N(i0)满足:pi0∈/N(i0);且N(i0) 以pi0为中心,则称N(i0)为一个克里金窗口.图3 给出一个半径r=3的克里金窗口:w1表示相应位置的像元被标记为未变化类,Con表示相应位置的像元属于冲突严重区域,需重新分配类别,w2表示相应位置的像元被标记为变化类.

图3 半径 r=3 的克里金窗口Fig.3 Kriging window with radius r=3

普通克里金能够估算未知点的最优属性值,提供估值误差.但在当前问题中,获取冲突严重像元是否发生变化的概率比获取其属性值更重要.指示克里金将类别标记变量视作区域化变量,为计算类别概率提供了一种途径.本研究借助指示克里金理论求解冲突严重像元属于w1和w2的概率:首先对冲突严重像元定义一个克里金窗口,并将窗口中已标记的像元视作已知点;然后通过指示克里金计算冲突严重像元的类别概率.

具体地,对任给冲突严重像元pi0,用Pro2(i0)表示其属于变化类w2的概率.为计算Pro2(i0),可从变化类的角度定义指标变量x2(i):将已标记为w2和w1像元的指标值分别设置为1 和0:对于冲突严重像元,其类别未知,发生和未发生变化的可能各占一半,故将Con1∪Con2中像元的指标值设置为 1/2 ,即

2 实验对比与分析

2.1 实验数据

为验证所提出的变化检测技术CAFI 的有效性,本研究采用三组来自不同传感器、具有不同变化类型的遥感数据进行实验.实验1 中使用的数据由内蒙古和黑龙江交界处的两幅Landsat-5 TM 影像构成,获取时间分别为2006年8月22日(t1)和2011年6月17日(t2),数据大小为1 200×1 350 像元.两期影像的变化主要是由森林火灾引起的.图4(a)～(c)给出两期影像及其变化参考图.本研究三组实验数据的变化参考图,均是通过人工详细对比两期遥感影像生成:白色表示发生变化区域,黑色表示未发生变化区域.实验1 使用影像的1～5 和7 波段进行变化检测.

图4 实验1 中使用的遥感影像及其变化参考图Fig.4 The remote sensing images used in Experiment 1 and its reference map

实验2 中使用的数据由辽宁省某地区的两幅Landsat-7 ETM + 影像构成,大小为800×1 000像元,成像时间分别为 2001年 8月 11日(t1)和2002年 8月 14日(t2).两期影像发生变化的主要原因是农作物种植的改变.图5(a)～(c)分别给出两期影像和它们的变化参考图.实验2 使用影像的1～4 波段进行变化检测.

图5 实验2 中使用的遥感影像及其变化参考图Fig.5 The remote sensing images used in Experiment 2 and its reference map

实验3 中使用的数据由湖南某地区的两幅Landsat-8 OLI(Operational land imager)影像构成,其大小为3 000×1 600 像元,获取时间分别为 2013年9月 17日(t1)和 2016年 7月 23日(t2).如图6(a)和图6(b)所示,该地区主要包括4 种地物:水、农田、森林和城区建筑.两期影像包含多种类型的变化,这些变化主要是由于长时间降雨、种植计划改变和城市建设造成的.

变化的多样性和较大的尺寸,使得实验数据3 的变化检测任务更具挑战性,同时也使得生成整个区域的变化参考图非常困难.受文献[9,20]的启发,实验3 中采用抽样技术进行性能评估.具体的,采用分层抽样技术选取8 组400×400 像元的影像块测试各算法的性能.这些影像块空间分布均衡,且包含所有变化类型.图6(c)给出了8 组影像块的变化参考图,实验3 使用影像的1～7 波段进行变化检测.

图6 实验3 中使用的遥感影像及其变化参考图Fig.6 The remote sensing images used in Experiment 3 and its reference map

首先对3 组影像进行配准和辐射校正等预处理,然后利用CVA,SCM,PCA 和SGD 生成两期影像的差异图集,最后利用FCM 生成每组差异图的模糊隶属度函数,得到每组差异图的变化检测图,为多差异图融合做准备.

2.2 实验设计

本文方法CAFI 在确定冲突严重像元过程中,涉及参数T1和T2,在重新分类冲突严重像元时,涉及参数克里金窗口半径r,故特组织实验测试参数Tk,k ∈{1,2}和r对CAFI 的影响.为证明CAFI的有效性,根据其特点组织了如下对比实验:1)与所使用的四组单差异图变化检测器进行比较,即CVA,SCM[19],PCA 和SGD[20];2)与四组先进融合技术进行比较:数据级融合技术HFV[13]:HFV 通过融合波谱强度变化和波谱角度生成差异图,决策级融合技术:投票法MV[9]、模糊积分FI(指Choquet 积分)和K 均值(K means,KM)聚类集成自适应投票法(Adaptive MV,AMV)的融合算法(Kmeans-based adaptive MV,KMAMV)[29];3)与三组先进水平的非融合算法比较:增强的模糊局部信息C 均值聚类(Reformulated fuzzy local information C-means,RFLICM)[10]、集成全局和局部信息的FCM聚类(FCM clustering incorporating both local and global information,FLGICM)[30],以及最优阈值技术Optimal-T:Optimal-T 对阈值T进行遍历,通过与变化参考图比较得到最优阈值的变化检测图.将Optimal-T 作为对比算法,是为了与最先进的阈值技术做比较(如文献[31]).

在4 组单差异图和HFV 方法中,得到差异图后通过FCM 获取变化检测结果.RFLICM、FLGICM和Optimal-T 基于最流行的CVA 生成的差异图实施变化检测.在FCM、RFLICM 和FLGICM 聚类中,将用来控制隶属度函数模糊度的模糊加权系数设置为2.在KMAMV 算法中,通过多次实验确定控制自适应分割过程的两个参数的取值,并采用KMAMV的最优检测结果参与后续对比分析.此外,以数据2 为例分析CAFI 的增强过程.

漏检错误(Missed detections,MD)、虚检错误(False alarms,FA)、总体错误(Overall errors,OE)和Kappa 系数[10]是4 种最常用的变化检测精度指标.MD 表示未被检测出的变化像元个数,FA表示被检测为变化类的未变化像元个数,OE= MD +FA.OE 和Kappa 系数是综合评价指标.因Kappa系数涉及更多分类信息,相比于其他指标更加可靠.

2.3 参数测试

本小节测试参数Tk,k ∈{1,2}和克里金窗口半径r对CAFI 的影响.为测试CAFI 对参数Tk,k ∈{1,2}的敏感度:令参数Tk在集合{0.5,1,1.5,2,2.5,3,3.5,4,4.5,5,5.5,6,6.5,7}上取值,将最可靠的Kappa 系数作为变化检测的评价标准.图7(a)～(c)给出(r=3 时)三组实验中CAFI 的Kappa 系数随T1和T2变化的曲面图,为清楚展示曲面变化趋势,只给出部分测试数据.

观察图7(a)～(c)可知,对三组实验数据,CAFI 的Kappa 系数随参数T1和T2具有类似的变化趋势:固定参数T1时,CAFI 的Kappa 系数随着T2的增大而升高;固定参数T2时,CAFI 的Kappa系数随着T1的增大而降低;当T1∈[0.5,1.5] ,T2∈[5,7]时,CAFI 的Kappa系数基本保持不变,且达到最优.Kappa 系数在区域([0.5,1.5],[5,7])保持稳定说明CAFI 对参数T1和T2具有一定鲁棒性.随后的对比分析中,CAFI 将参数Tk固定为T1=1,T2=6.

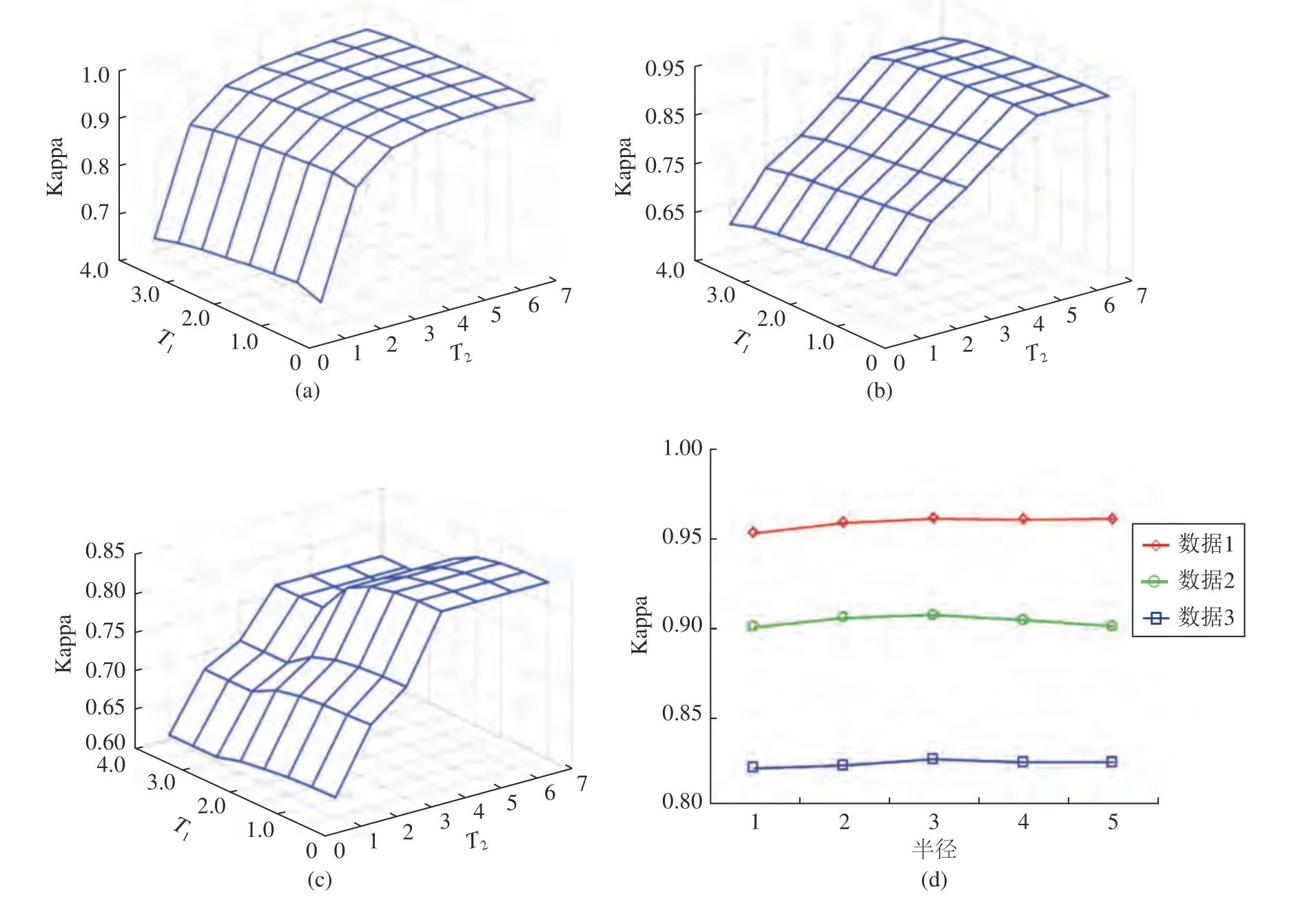
图7 参数分析图((a)～(c)Kappa 系数随参数 T1 和 T2 的变化曲面;(d)Kappa 系数随半径 r 的变化曲线)Fig.7 Diagram of parameter analysis((a)～(c)changing surface of Kappa coefficients with parameters T1 and T2 and(d)relationships between KC and radius r for the three datasets)

为测试克里金窗口半径r对CAFI 的影响,令r在集合{1,2,3,4,5}上取值.图7(d)给出(T1=1,T2=6)CAFI 的Kappa 系数随半径r的变化曲线图.从图7(d)可知,对三组实验数据,当半径r从1 变到3 时,Kappa系数缓慢上升;当半径r从3变到5 时,Kappa 系数略有下降.实验结果表明CAFI 对参数r具有一定的鲁棒性.随后的对比分析中CAFI 将参数r的取值固定为3.需要指出的是,克里金窗口半径r的最优取值与影像的分辨率有关,当将CAFI 应用到分辨率远高于(或远低于)本研究使用数据分辨率的遥感影像时,需重新测试确定克里金窗口半径的取值.

2.4 实验结果对比与分析

图8 给出通过CVA、SCM、PCA 和SGD 得到的第1 组实验数据的4 组差异图.图9 给出第1 组实验数据的变化检测图:图9(a)～(d)分别为通过FCM 得到的CVA、SCM、PCA 和SGD 的变化检测图:图9(e)～(l)分别为Optimal-T、RFLICM、FLGICM、HFV、MV、KMAMV、FI 和本文方法CAFI 的检测图:黑色表示未变化区域,白色表示变化区域,红色表示漏检区域,黄色表示虚检区域.表2 给出第1 组实验数据变化检测结果的定量分析指标.

从图8 可知:CVA、SCM、PCA 和SGD 得到信息互补的差异图集.SCM 和PCA 的差异图能够有效地抑制未变化区域像元的灰度值强度,有利于减少虚检;但同时也使得部分变化区域像元具有较小的灰度值,容易造成漏检.CVA 和SGD 差异图变化区域像元的灰度值相对均匀,有利于降低漏检;但其变化区域和未变化区域像元灰度值的对比度相对较低,容易造成虚检.虽然SCM 和PCA(CVA和SGD)的差异图具有一定的相似特征,但仔细观察可发现它们亦具有明显不同.4 组差异图的检测结果(图9(a)～(d))也验证了CVA、SCM、PCA和SGD 的互补性:4 组变化检测图互不相同,总的来讲,差异图SCM 和PCA 的检测图中虚检错误(黄色区域)较少,但漏检错误(红色区域)较多;而CVA 和SGD 的检测图中漏检相对较少,但虚检错误严重(表2).互补的检测结果为融合技术提高变化检测精度提供了可能.

图8 通过CVA、SCM、PCA 和SGD 得到的第1 组实验数据的4 组差异图Fig.8 The four difference images obtained by CVA,SCM,PCA,and SGD on Dataset 1

图9 不同检测技术对第1 组实验数据的变化检测结果Fig.9 Change detection results obtained by different methods on Dataset 1

表2 第1 组实验数据变化检测结果的定量分析指标Table 2 Quantitative analysis indices for change detection results on Dataset 1

对4 组单差异图检测器,SCM 的检测结果优于其他3 组差异图(表2).对其余对比算法,Optimal-T、RFLICM、FLGICM、HFV 和MV 得到了优于CVA 的变化检测图,但其检测图中仍包含大片黄色虚检(图9(e)～(i)).与Optimal-T、RFLICM、FLGICM、HFV 和MV 相比,KMAMV 和FI 的虚检错误有所减少,得到更优的变化检测结果(表2),但其检测结果仍不够理想,其检测图中还有较多的黄色虚检错误(图9(j)和图9(k)).

虽然FI 对冲突较弱像元能够得到较可靠的融合结果,但其不能很好地处理冲突严重像元,影响了整体融合效果.所提出的CAFI 通过识别和重新分类冲突严重像元,显著增强了FI 的性能,得到最接近变化参考图的检测图(图9(l)):一方面CAFI 去除了FI检测图中的几乎全部黄色虚检错误;另一方面CAFI检测图中包含的红色漏检最少.表2 从定量的角度表明CAFI 优于其他检测技术:其总体错误最小,Kappa系数最高.例如,CAFI 的Kappa 系数为0.9613,比CVA,SCM,PCA,SGD,Optimal-T,RFLICM,FLGICM,HFV,MV,KMAMV 和FI 分别提高35.76 %,5.46 %,9.05 %,7.61 %,17.02 %,25.14 %,14.52 %,16.38 %,9.59 %,6.02 %和7.54 %.

图10 给出第2 组实验数据的变化检测结果:图10(a)～(l)分别为CVA、SCM、PCA、SGD、Optimal-T、RFLICM、FLGICM、HFV、MV、KMAMV、FI 和本文方法CAFI 的变化检测图:(m)为CAFI识别的冲突严重像元的空间分布.表3 给出实验数据2 检测结果的定量分析指标.

通过图10 和表3 可知,实验2 得到与实验1类似的结果:对第2 组实验数据,4 组差异图亦得到互补的变化检测图:CVA 和SGD 的变化检测图包含较少的红色漏检和较多的黄色虚检错误,而SCM和PCA 的检测图则包含少量的虚检和大片的漏检(图10(a)～(d)和表3).实验结果表明CVA、SCM、PCA和SGD 能够提供互补的差异图,有望通过融合技术提高差异图变化检测的精度.

4组单差异图检测器中,SGD 的检测结果最优(表3).对其他7 种对比算法:Optimal-T 和RFLICM 得到比SGD 略差的检测结果:FLGICM、HFV、MV、KMAMV 和FI 得到比SGD略优的检测结果(图10(e)～(k)和表3).然而,HFV 和MV检测图中仍具有较多黄色虚检,FLGICM、KMAMV和FI 的检测图中具有较多红色漏检,影响了整体检测效果.

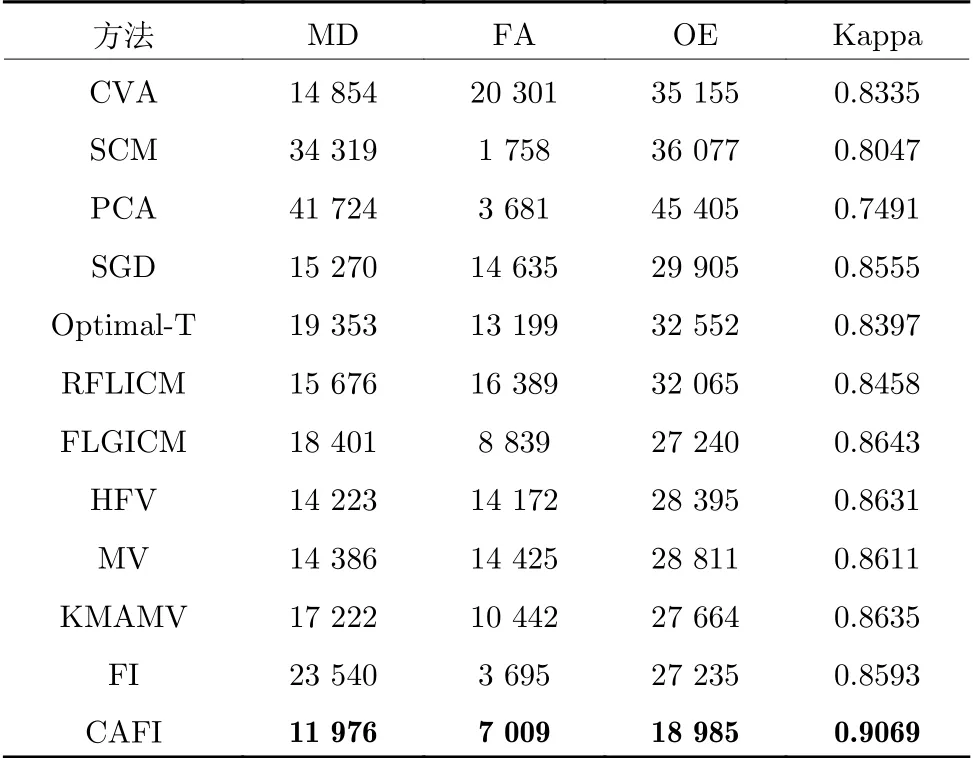
表3 第2 组实验数据变化检测结果的定量分析指标Table 3 Quantitative analysis indices for change detection results on Dataset 2

实验2 中,所提出的CAFI 再次战胜11 组对比算法,得到最准确的变化检测图,检测图中彩色面积最少(图10(l)).从定量的角度,CAFI 具有最小的漏检错误和总体错误,最高的Kappa 系数(表3):其总体错误为18 985 像元,比其他检测技术降低超过8 000 像元;其Kappa 系数为0.9069,比其他技术提高4.26 %～15.78 %.

图10 不同检测技术对第2 组实验数据的变化检测结果Fig.10 Change detection results obtained by different methods on Dataset 2

对第3 组实验数据,图11 给出各检测技术的变化检测图,表4 给出各变化检测图的定量分析指标.由于第3 组实验数据尺寸较大,很难在一页纸上展示其检测图的细节.为便于视觉分析,选取两个典型的影像块(即影像块A和F)进行视觉比较.图12 和图13 给出了影像块A和F的原始影像、变化参考图和各检测技术的变化检测图.表4 中的定量分析指标是基于所有8 个影像块计算的(图6(c)).

图11 不同检测技术对第3 组实验数据的变化检测结果Fig.11 Change detection results obtained by different methods on Dataset 3

通过影像块A和F的变化检测图,可发现对第3 组实验数据CVA、SCM、PCA 和SGD 也得到互补的检测结果(图12(d)～(g),图13(d)～(g)):SCM 和PCA 检测图中的黄色虚检错误较少,而SGD 检测图中的红色漏检相对较少.为通过融合技术增强单差异图检测器的性能提供潜力.对于其他7 组对比算法,除RFLICM、FLGICM 和KMAMV 外,另外4 组方法均得到了优于单差异图检测器的检测精度(表4).然而,Optimal-T、HFV 和MV 的检测图中仍具有许多虚检(影像块A),FI 的检测图中具有较多的红色漏检(影像块F).对更具挑战性的第3 组实验数据,本文方法CAFI 也得到了最接近变化参考图的变化检测图(图12(o),图13(o)).在定量分析方面,相比于其他11 种基准检测技术,CAFI 的总体错误明显降低,Kappa 系数显著提高(表4).CAFI 具有最高的Kappa 系数,比其他检测技术提高超过5 %.

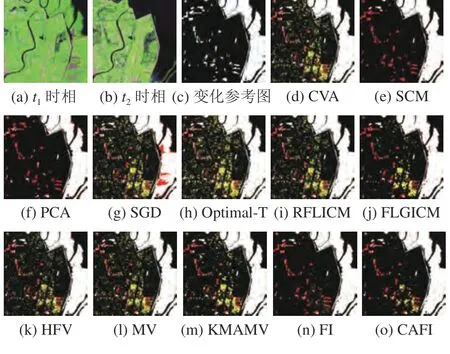
图12 影像块A 及其变化检测结果Fig.12 Image blocks A and its change detection results on Dataset 3

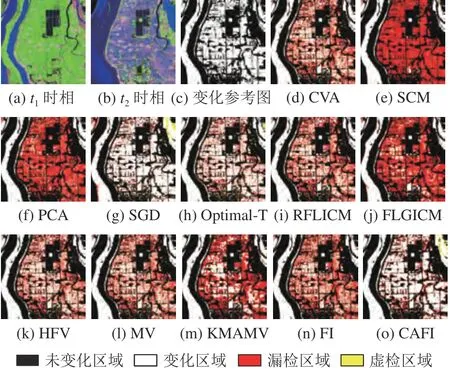
图13 影像块F 及其变化检测结果Fig.13 Image blocks F and its change detection results on Dataset 3

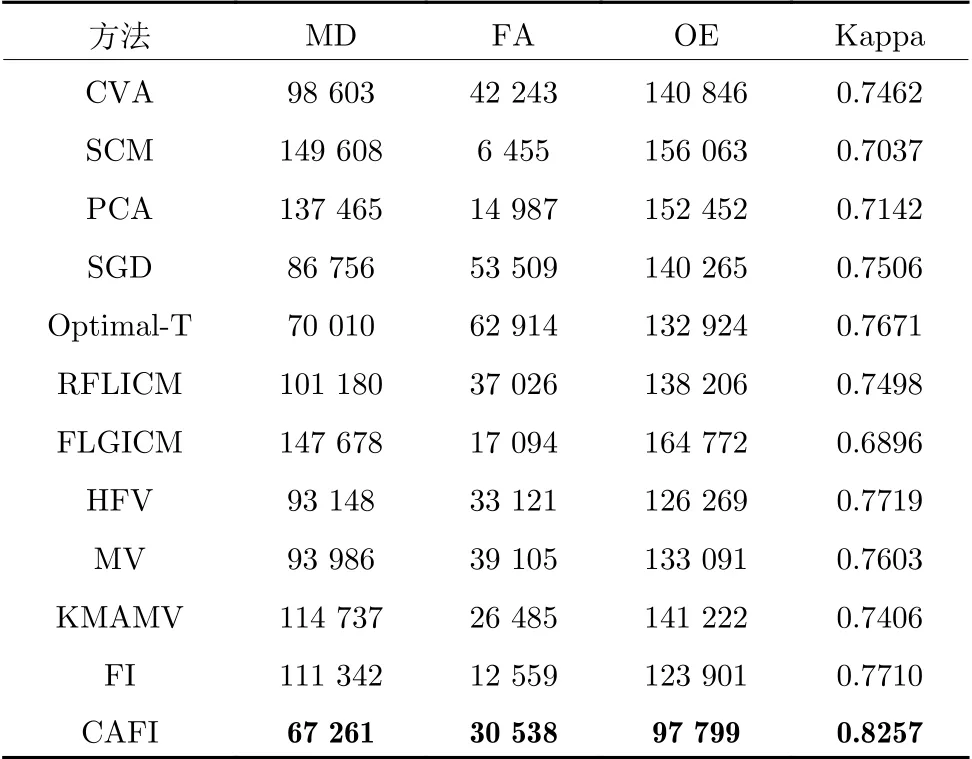
表4 第3 组实验数据变化检测结果的定量分析指标Table 4 Quantitative analysis indices for change detection results on Dataset 3

对来自不同传感器(TM、ETM+和OLI)、具有不同尺寸(1 200×1 350 像元、800×1 000 像元和3 000×1 600 像元)、不同变化类型(火灾(数据1),作物种植变化(数据2),包括持续降雨、作物种植改变和城市建设等引起的多种变化类型(数据3))的3 组真实遥感数据,所提出的CAFI 算法均战胜11组基准变化检测技术,取得最优的检测结果.而11组对比算法对3 组实验数据表现出不稳定的检测性能:对数据1,SCM 取得11 组对比算法中最高Kappa 系数(表2);对数据2,FLGICM 取得11 组对比算法中最高Kappa 系数(表3);对数据3,HFV 取得11 组对比算法中最高Kappa系数(表4).相比于11 组对比算法,CAFI 具有更好的鲁棒性.

2.5 增强过程分析

3组实验结果表明,本文方法CAFI 能够取得较优的变化检测结果.这主要是因为CAFI 集成不同信源优势的同时,通过识别和重新分类冲突严重像元,能够很大程度上解决FI 融合过程中的信源冲突问题.

接下来以实验数据2 为例说明重新分类步骤的效果.图10(m)展示CAFI 识别的数据2 的冲突严重像元的空间分布.表5 列出各检测技术对冲突严重像元的检测结果:OE表示总体错误,ConOE表示冲突严重像元的总体错误,PConOE表示ConOE占OE的百分比,即PConOE=ConOE/OE×100%,ConA表示冲突严重像元的检测精度.

由于干扰的多样性、地物变化的复杂性、以及差异图生成算子的局限性,使得在许多像元处,单差异图检测器具有相互冲突的变化检测结果(图10(m)).这些冲突像元在融合过程中容易造成融合错误,是影响融合效果的主要因素.比如,FI 在冲突区域有20 779 个检测错误像元,约占其总体错误(27 235)的76 %(表5).通过识别和重新分类步骤,CAFI能够显著提高FI 处理冲突严重像元的能力,增强其性能.CAFI 对冲突严重像元的检测精度为85.68 %,比FI 提高9 %以上,比其他检测技术提高6.5 %以上.

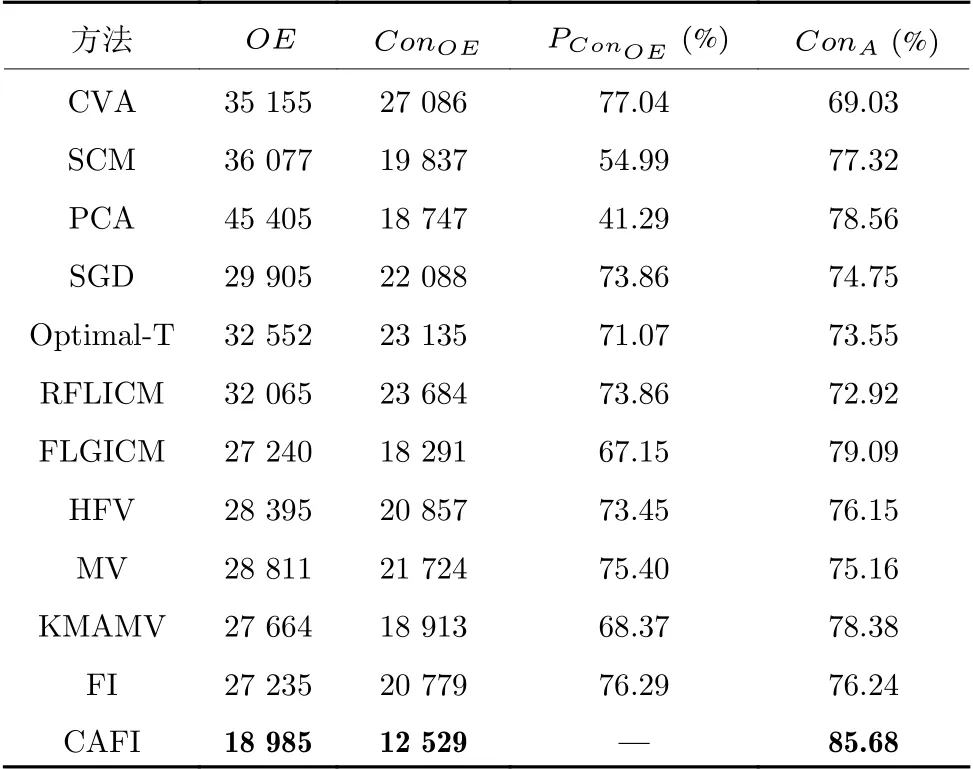
表5 实验2 中的冲突严重像元的变化检测结果Table 5 Change detection results on strongly conflicting pixels in Experiment 2

3 结束语

本文提出一种全自动的顾及冲突分析的融合变化检测技术CAFI.CAFI 不仅能够集成不同信源的优势,且能够很大程度上解决FI 融合过程中的信息冲突问题.三组来自不同传感器、具有不同变化类型数据的实验结果表明:CAFI 的检测效果优于CVA、SCM、PCA、SGD、Optimal-T、RFLICM、FLGICM、HFV、MV、KMAMV 和FI 等11 组基准变化检测技术.CAFI 具有良好的扩展性:本文对4 组信源进行融合,可灵活增减信源个数;可直接将CAFI扩展到多算法情形:将不同算法应用到同一数据,对不同算法的结果进行融合.

对中高分辨率遥感影像,CAFI 能够取得较优的检测结果,如本文中数据.今后的工作重点是将CAFI 应用到更高分辨率的遥感影像,这需要根据使用影像的特点,调整生成差异图集的策略.