随机梯度下降算法研究进展

史加荣 王 丹 尚凡华 张鹤于

1.西安建筑科技大学理学院 西安 710055 2.省部共建西部绿色建筑国家重点实验室 西安 710055 3.西安电子科技大学人工智能学院智能感知与图像理解教育部重点实验室 西安 710071 4.西安电子科技大学计算机科学与技术学院 西安 710071

作为人工智能目前最活跃的一个研究分支,机器学习根据经验数据来设计、开发算法,其目的是探索数据的生成模式,并用来发现模式和进行预测[1-2].深度学习是一类更广的机器学习方法,允许由多个处理层组成的计算模型来学习具有多个抽象级别的数据表示[3].伴随着深度学习的崛起,机器学习重新受到了学术界和工业界的广泛关注.机器学习技术已广泛地应用在计算机视觉、推荐系统、语音识别和数据挖掘等领域中.

回归与分类等监督学习是机器学习中最常见的一类学习问题,它提供了包含输入数据和目标数据的训练数据集.为了探讨输入与目标之间的关系,需要先建立含参数的表示模型,再通过最小化所有样本的平均损失函数来获得最优的参数,此处的优化模型通常为经验风险最小化(Empirical risk minimization,ERM)[4].梯度下降法是求解ERM 模型最常用的方法,也是二阶方法和黎曼优化的重要基础.传统的梯度下降法在计算目标函数的梯度时,需计算每个样本对应的梯度,总计算复杂度线性地依赖于样本数目.随着数据规模的日益增大,求解所有样本的梯度需要相当大的计算量,因而传统的梯度下降算法在解决大规模机器学习问题时往往不再奏效[5].

随机梯度下降算法(Stochastic gradient descent,SGD)源于1951年Robbins 和Monro[6]提出的随机逼近,最初应用于模式识别[7]和神经网络[8].这种方法在迭代过程中随机选择一个或几个样本的梯度来替代总体梯度,从而大大降低了计算复杂度.1958年Rosenblatt 等研制出的感知机采用了随机梯度下降法的思想,即每轮随机选取一个误分类样本,求其对应损失函数的梯度,再基于给定的步长更新参数[9].1986年Rumelhart 等分析了多层神经网络的误差反向传播算法,该算法每次按顺序或随机选取一个样本来更新参数,它实际上是小批量梯度下降法的一个特例[9].近年来,随着深度学习的迅速兴起,随机梯度下降算法已成为求解大规模机器学习优化问题的一类主流且非常有效的方法.目前,随机梯度下降算法除了求解逻辑回归、岭回归、Lasso、支持向量机[10]和神经网络等传统的监督机器学习任务外,还成功地应用于深度神经网络[11-12]、主成分分析[13-14]、奇异值分解[13,15]、典型相关分析[16]、矩阵分解与补全[17-18]、分组最小角回归[19-20]、稀疏学习和编码[21-22]、相位恢复[23]以及条件随机场[24]等其他机器学习任务.

随着大数据的不断普及和对优化算法的深入研究,衍生出随机梯度下降算法的许多不同版本.这些改进算法在传统的随机梯度下降算法的基础上引入了许多新思想,从多个方面不同程度地提升了算法性能.搜索方向的选取和步长的确定是梯度下降算法研究的核心.按照搜索方向和步长选取的方式不同,将随机梯度下降算法的改进策略大致分为动量、方差缩减、增量梯度和自适应学习率等四种类型.其中,前三类方法主要是校正梯度或搜索方向,适用于逻辑回归、岭回归等凸优化问题;第四类方法针对参数变量的不同分量自适应地设置步长,适用于深度神经网络等非凸优化问题.

在传统梯度下降算法的基础上添加动量项可以有效避免振荡,加速逼近最优解.采用动量更新策略的方法主要包括经典动量算法(Classical momentum,CM)[25]和Nesterov 加速梯度算法(Nesterov＇s accelerated gradient,NAG)[26-27].简单版本的随机梯度下降算法在随机取样的过程中产生了方差并且随着迭代次数的增加而不断累加,无法保证达到线性收敛.为此,研究者们相继提出了一系列基于方差缩减的随机梯度下降算法,主要包括随机方差缩减梯度算法(Stochastic variance reduced gradient,SVRG)[28]、近端随机方差缩减梯度算法(Proximal stochastic variance reduction gradient,Prox-SVRG)[29]、Katyusha[30]和MiG[31]等.前述方法没有充分利用历史梯度信息,而增量梯度策略通过“以新梯度替代旧梯度”的方式,充分考虑了历史梯度且达到了减少梯度计算量的目的,该类型的主要算法包括随机平均梯度算法(Stochastic average gradient,SAG)[32]、SAGA[33]和Point-SAGA[34].Allen-Zhu[30]根据算法在强凸条件下的复杂度将前三类随机梯度下降算法分为三代,复杂度随代数的增加而降低.在深度神经网络中,自适应学习率的随机梯度下降法通过使用反向传播所计算出的梯度来更新参数[35].与前三类算法不同,自适应算法在训练过程中会根据历史梯度信息,针对参数的不同分量自动调整其对应的学习率.这类算法主要包括Adagrad[36]、Adadelta[37]、Adam(Adaptive moment estimation)[38]和Nadam(Nesterov-accelerated adaptive moment estimation)[39]等.

目前,各种版本的随机梯度下降算法大多以黑箱优化器的形式在TensorFlow、PyTorch 和Mx-Net 等各大主流平台供用户调用,但背后的算法原理却鲜为人知.2017年Ruder 在文献[40]中介绍了几种深度学习领域中的随机梯度下降算法,但缺乏一些最新的研究成果、算法之间的联系以及实际数据集上的实验对比.国内学者提出过一些随机梯度下降算法的改进策略,但尚未有人发表过此方向的综述性论文.因此,本文的工作对于关注梯度下降算法理论及其在深度学习中应用的研究者具有参考意义.本文针对随机梯度下降算法展开研究,讨论了动量、方差缩减、增量梯度和自适应学习率等四类更新策略下主要算法的核心思想、迭代公式以及算法之间的区别与联系.对于逻辑回归、岭回归、Lasso 和深度神经网络等机器学习任务,设计了相应的数值实验,并对比了几种具有代表性的随机梯度下降算法的性能.文末对研究工作进行了总结,并展望了随机梯度下降算法面临的挑战与未来的发展方向.

1 预备知识

本节先引入经验风险最小化模型,再简要介绍凸优化的基本知识,最后给出了3 类梯度下降算法.

1.1 经验风险最小化

1.2 凸优化基础知识[41]

1.3 梯度下降算法

图1 条件数对收敛速度的影响Fig.1 Effect of conditional number on convergence speed

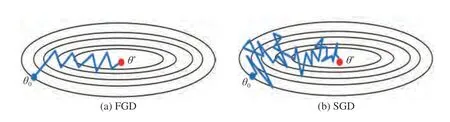
图2 FGD 和SGD 的优化轨迹示意图Fig.2 Schematic diagram of optimization process of FGD and SGD

2 基于动量的随机梯度下降算法

SGD 所生成的梯度方向常与目标函数的峡谷长轴垂直,并沿其短轴来回振荡,因此目标参数在长轴上缓慢移动,无法快速到达目标函数的谷底.物理学中的“动量”可以有效地避免峡谷中的振荡,从而加快在长轴上的位移.Qian[25]证明了结合动量的梯度下降算法与保守力场中的牛顿粒子运动具有统一性,从而得出了在梯度下降算法基础上添加动量项可以提升优化效率的结论.

2.1 随机经典动量算法

2.2 Nesterov 加速梯度算法

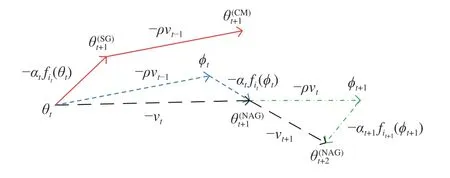
图3 SGD、CM 和NAG 的参数更新示意图Fig.3 Schematic diagram of parameters update of SGD,CM and NAG

3 基于方差缩减的随机梯度下降算法

在SGD 中,单个样本的梯度是全体样本平均梯度的无偏估计,但梯度方差往往随着迭代次数的增加而不断累加,这使得SGD 无法保证能够达到线性收敛[49].“方差缩减” 策略通过构造特殊的梯度估计量,使得每轮梯度的方差有一个不断缩减的上界,从而取得较快的收敛速度.

3.1 随机方差缩减梯度算法

3.2 近端随机方差缩减梯度算法

SVRG 能够加快收敛速度,但只适用于光滑的目标函数.对于添加了非光滑正则项的目标函数,虽然可以通过计算次梯度来近似替代梯度,但收敛速度较慢,实际意义较小.随机近端梯度下降算法(Stochastic proximal gradient descent,SPGD)通过计算投影算子间接地估计目标参数,从而巧妙地避开了正则项不光滑的问题[50-51].近端随机方差缩减梯度算法(Prox-SVRG)将SVRG 与SPGD 相结合,为含非光滑正则项的目标函数使用方差缩减技巧提供了解决方案[29].考虑模型(1)的正则化版本

3.3 Katyusha 算法

3.4 MiG 算法

表2 几种方差缩减算法的动量类型Table 2 Momentum types of several variance reduced algorithms

Shamir[13]将方差缩减技术应用在主成分分析中,并提出了方差缩减主成分分析(Variance reduced principal component analysis,VR-PCA).Shang 等[53]通过调整SVRG 的关键点设置,提出了适用于大步长的方差缩减随机梯度下降算法(Variance reduced SGD,VR-SGD).此外,包含方差缩减思想的随机梯度下降算法还有随机对偶坐标上升(Stochastic dual coordinate ascent,SDCA)[54]以及随机原对偶坐标(Stochastic primal-dual coordinate,SPDC)[55]等.

4 基于增量梯度的随机梯度下降算法

“增量梯度” 策略源于增量聚合梯度算法(Incremental aggregated gradient,IAG)[56],该算法为每个样本保留一个相应的梯度值,在迭代过程中,依次抽取样本并用新梯度替代旧梯度.

4.1 随机平均梯度算法

4.2 SAGA

4.3 Point-SAGA

表3 SVRG 与增量算法参数更新公式对比Table 3 Comparison of parameters updating formulas among SVRG and incremental algorithms

对于前述几种非自适应学习率的随机梯度下降算法,Allen-Zhu[30]根据各算法在强凸条件下的复杂度将其分为3 代.第1 代算法包括SGD 和NAG等;第2 代包括SVRG 和Prox-SVRG 等;第3 代包括Katyusha 和Point-SAGA 等.其中,第1 代算法的复杂度最高.在多数情形下,第3 代算法的复杂度优于第2 代算法的复杂度,当n ＜κ时优势尤其显著.对于动量、方差缩减和增量梯度策略下的随机梯度下降算法,表4 比较了各算法取得ε-近似解的复杂度和收敛速度,其中,常数ρ ∈(0,1),T=t/n表示全局迭代次数.

表4 随机梯度下降算法的复杂度与收敛速度Table 4 Complexity and convergence speed of stochastic gradient descent algorithms

5 自适应调节学习率的随机梯度下降算法

在大规模机器学习中,为了减少振荡、提高优化效率,每经过数轮迭代就需要更换一个较小的学习率.手动调节学习率工作量较大且很难快速找到当前模型环境下的最佳值.若设置的学习率过小,会使得优化进程缓慢;若学习率过大,会导致振荡且难以逼近最优解甚至逐渐远离最优解,如图4所示.为了解决此问题,一些学者提出了以下几种自适应调节学习率的随机梯度下降算法,这些算法在深度神经网络中表现出了极佳性能.

图4 学习率对优化过程的影响Fig.4 Effect of learning rates on optimization process

5.1 Adagrad

对于数据特征不平衡的问题,若使用SGD,则稀疏特征对应的梯度分量的绝对值很小甚至为零,这使得目标参数难以逼近最优解.Adagrad[35]是一种自适应调节学习率的随机梯度下降算法,它将目标参数θ的分量进行拆分,对每个分量使用不同的学习率进行更新.对稀疏特征相应的参数分量使用较大的学习率进行更新,进而识别出那些非常具有预测价值但易被忽略的特征.

Dean 等[60]发现Adagrad 能显著提高SGD 的鲁棒性,并将其用于谷歌的大型神经网络训练;Pennington等[61]在训练词嵌入技术时使用了Adagrad,这是因为不常用的词比常用的词需要更大的更新.Chen 等[62]提出了SAdagrad,它将Adagrad 看作一个子程序并周期性调用,在强凸条件下具有更好的收敛速度.Adagrad 的提出使人们摆脱了手动调节学习率的困扰,但仍存在以下缺点:1)历史梯度无节制地累加导致了学习率不断衰减至一个极小的数,这使得训练后期优化效率很低;2)需要预先设置全局学习率;3)保留梯度的内存成本过大.

图5 Adagrad 的学习率变化示意图Fig.5 Schematic diagram of learning rate changes for adagrad

5.2 Adadelta

5.3 Adam

5.4 AdaMax

5.5 Nadam

Nadam 将Nesterov 动量加入到Adam 中,以提升Adam 的算法性能,亦可看作是Adam 和NAG的结合[39].从表1 可以看出:要将CM 转化为NAG,需要添加中间变量.只要统一Adam 与CM 的更新形式,便可使用这种修改技巧实现从Adam 向Nadam 的转换.

表1 CM 与NAG 的更新公式比较Table 1 Comparison of update formulas between CM and NAG

随着深度学习网络模型越来越复杂,自适应算法面临着泛化性能差、学习率逐渐极端化等问题.在最近的几个自然语言处理和计算机视觉项目中,自适应算法仅在训练初期的优化效率较高,而在训练后期和测试集上常常出现停滞不前的情况,且整体效果不及SGD 与NAG[67-68].Reddi 等[69]认为可以通过对过去梯度的“长期记忆” 来解决自适应算法收敛性差的问题,并提出Adam 的改进算法AmSGDrad,此算法有效地提升了收敛速度.Luo 等[70]提出的自适应算法Adabound 为学习率设置了一个动态上界,且初始化学习率上界为无穷大,随着迭代次数的增加,学习率最终平稳地递减至一个恒定的值.Adabound在训练初期的优化速度与Adam 相当,在训练后期性能稳定且泛化能力较强,能够在复杂的深层网络中发挥良好的性能.

6 数值实验

先使用动量、方差缩减和增量梯度3 种策略下的随机梯度下降算法解决逻辑回归等机器学习任务,再将自适应学习率的随机梯度下降算法应用到深度卷积神经网络中.

6.1 非自适应学习率算法的性能对比

本节实验对非自适应学习率的随机梯度下降算法在机器学习模型中的性能进行对比.采用MATLAB 与C 语言混合编程,涉及的算法程序均在4 核AMD A10-7300 Radeon R6 处理器上运行.实验所用的Adult 等4 个数据集均来自于UCI 机器学习库(http://archive.ics.uci.edu/ml/datasets.html).表5给出了这些数据集的详细信息.

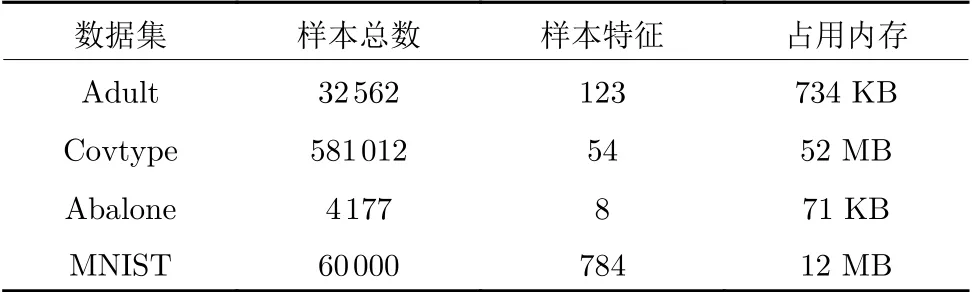
表5 数据集描述Table 5 Description of datasets

建立ℓ2逻辑回归(ℓ2-Logistic regression)、岭回归(Ridge regression)和Lasso 等3 种经典机器学习模型.表6 列出了3 种优化模型的公式,其中‖·‖1为向量的ℓ1范数,λ1和λ2为取正值的正则化系数.显然,前两种是光滑且强凸的优化模型,第3种是非光滑凸的优化模型.表7 列出了4 个实验数据集对应的优化模型及正则参数设置.选取SGD、NAG、SVRG、SAGA、Katyusha 以及MiG共6 种具有代表性的方法进行实验,通过研究6 种算法的迭代效率和时间效率,对比、分析算法的实际性能.为公平起见,初始化目标参数为零向量,每种方法的超参数和学习率均先按照理论最优值进行设置,再结合具体实验进行微调,以使算法的实际性能达到最佳.

表6 3 种机器学习任务的优化模型Table 6 Optimization models for 3 machine learning tasks

表7 数据集对应的优化模型与正则参数Table 7 Optimization model and regularization parameter for each dataset

图6 比较了6 种随机梯度下降算法的迭代效率,其中,横坐标表示全局迭代次数,纵坐标表示当前目标函数值与最优目标函数值之差.从图6 可以看出,第1 代随机梯度下降算法SGD 和NAG 的迭代效率较低,难以在较少的迭代次数内逼近最优解,这可能是因为梯度的方差不断累积且实际数据集存在噪声.作为简单版本的随机梯度下降算法,SGD迭代效率最低;NAG 添加了Nesterov 动量,尽管在一定程度上提升了SGD 的优化效率,但效果并不显著.第2 代随机梯度下降算法的迭代效率在第1 代的基础上产生了质的飞跃.SVRG 和SAGA 分别通过采用方差缩减与增量梯度的策略构造相应的梯度估计量,有效限制了方差的累积,极大地提升了算法性能,且能够在较少的迭代次数内逼近最优解.第3 代随机梯度下降算法Katyusha 和MiG 在方差缩减技术的基础上添加了消极动量,因此在目标参数的优化过程中更加稳健、精准、高效,能够在极少的迭代次数内逼近最优解.

图7 对比了6 种随机梯度下降算法的时间效率,其中:横坐标表示运行时间,纵坐标表示当前目标函数值与最优目标函数值之差.从图7 可以看出:第2 代和第3 代随机梯度下降算法的时间效率明显强于第1 代,这与图6 中迭代效率的对比情况相似.此外,第3 代算法的整体时间效率虽然稍强于第2代算法,但其优势并不像迭代效率那样显著.第3代算法虽然在复杂度和收敛速度上都有明显优势,但由于自身结构相对复杂,故在实际应用中单次迭代的计算量较大、运行时间较长.

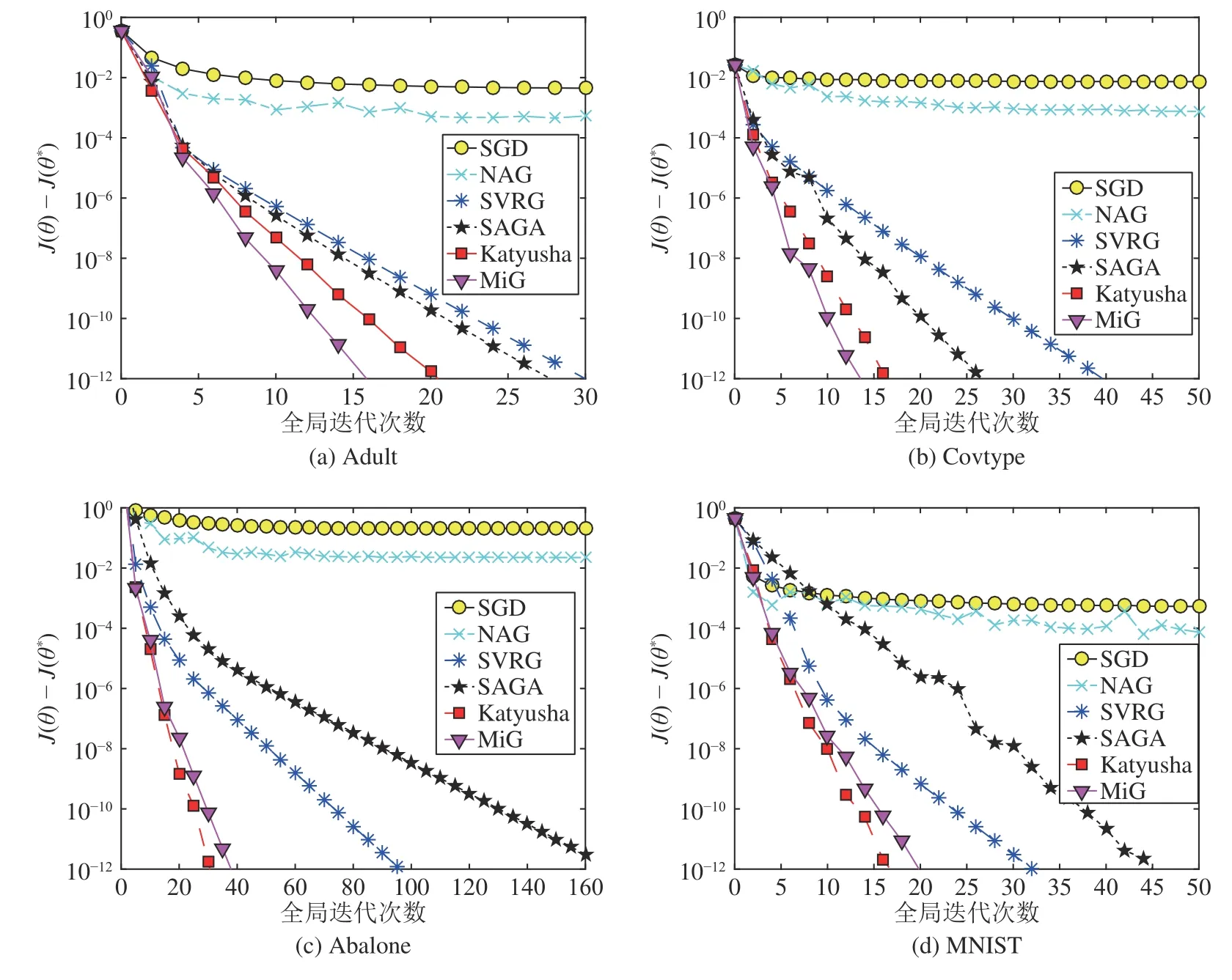
图6 随机梯度下降算法的迭代效率对比Fig.6 Comparison of iterative efficiency of stochastic gradient descent algorithms

图7 随机梯度下降算法的时间效率对比Fig.7 Comparison of time efficiency of stochastic gradient descent algorithms

6.2 自适应学习率算法的性能对比

本节实验对自适应学习率的随机梯度下降算法在深度学习中的性能进行对比.实验环境为MxNetgluon 1.0,工作站配置了10 核Intel Xeon E5-2640v4处理器和两块GTX 1080ti 11 GB 显卡.使用的CIFAR-10 数据集(http://www.cs.toronto.edu/～kriz/cifar.html)包含60 000 幅32 × 32 × 3 的彩色图像.根据图像内容可将其分为“飞机”、“鸟” 和“猫”等10 个类别,其中每个类别均包含6 000 幅图像.从每类图像中随机选取5 000 幅作为训练样本,剩余的1 000 幅作为测试样本,并在实验过程中采取数据增广策略.

在ResNet-18 卷积神经网络模型[71]下,对Adagrad、Rmsprop、Adadelta 以及Adam 的实际性能进行比较.此外,实验还考虑了SGD 和CM 两种非自适应算法.ResNet-18 网络模型的权重参数按均值为0、标准差为0.01 的正态分布随机初始化.训练时采用交叉熵损失函数,批容量为32,除Adadelta 外,其余算法全局学习率的初始值均为 10-3,且每隔30 代衰减至之前的1/10,共训练90 代.

图8 展示了实验中训练集损失函数值、训练集精度以及测试集精度的变化情况.从此图可以看出,4 种自适应学习率的梯度下降算法在实验中的性能整体优于SGD.Adagrad 的性能最差,仅略优于SGD,这可能是因为Adagrad 生成的自适应学习率无节制减小,从而导致后期学习率微小,以至于无法突破局部最优点.Rmsprop 与Adadelta 的性能比较接近,且优于Adagrad.Adam 在训练集与测试集中的优化效率都是最高的,这说明矩估计思想和自动退火形式在随机梯度下降算法中起到了提升算法性能的作用.此外,CM 在训练集中的表现与Rmsprop相当,在测试集中的性能甚至略优于Rmsprop.

图8 自适应学习率的随机梯度下降算法性能比较Fig.8 Performance comparison of stochastic gradient descent algorithms with adaptive learning rates

7 总结与展望

本文对近年来随机梯度下降算法的研究进展及主要研究成果进行了综述.根据算法的更新策略,将几种具有代表性的随机梯度下降算法分为四类,包括基于动量的算法、基于方差缩减的算法、基于增量梯度的算法以及自适应学习率的算法.本文介绍了这些算法的原理、核心思想以及相互之间的区别与联系,并通过数值实验对算法的实际性能进行了对比.实验结果表明:在逻辑回归等经典机器学习任务中,Katyusha 和MiG 等第3 代算法普遍具有较好的性能,而SGD 和NAG 等第1 代算法的实验性能最差;在深度卷积神经网络中,Adam 的实验性能最好.当前,国内外提出的随机梯度下降算法种类繁多,但理论不完善且评价标准尚未统一.因此,随机梯度下降算法仍将是未来的研究热点.

下面几个方向在今后的研究中值得关注.

1)与二阶算法相比,随机梯度下降算法的收敛速度相对较慢,且需要更多的迭代次数.第2 代和第3 代改进算法虽然有效地提升了收敛速度,但耗费了较大的时间成本和内存成本.随着数据规模的扩大和模型复杂度的提升,单线程下的随机梯度下降算法已经不能满足大规模机器学习应用的需求[72-73].Zinkevich 等[74]提出了首个并行式随机梯度下降算法SimuParallelSGD,这种方法适合于大规模学习范式和MapReduce 框架.文献[75]提出了Hogwild ! 算法,它对稀疏数据采用无锁异步更新策略,从而有效地减少了特征更新时的冲突.陈振宏等[76]提出了一种基于差异合并的分布式随机梯度下降算法DA-DSGD,从性能的加权合并、模型规范化两方面提高了算法性能.目前,研究者们已经实现了SVRG、SAGA 和MiG 等改进算法的分布式和并行化版本,但收敛速度却有待进一步提升[31,77-78].如何根据算法特点、数据对象和应用平台,设计并实现不同改进策略下的随机梯度下降算法的分布式与并行化版本,使其在实际应用中发挥出较高的性能水平,这是未来值得探索的问题.

2)学习率是随机梯度下降算法中一个非常重要的超参数,直接影响算法在实际应用中的性能.一些学者按照αt=c1/(tv+c2)的形式对每轮学习率进行设置,但这种形式在实际应用中收敛速度较慢,且c1,c2和v的取值仍难以确定[79].另一些学者则认为应先在固定步长下快速寻找最优解的邻域,再考虑更为精确的优化方案[80].目前,寻找最优学习率在理论和实践上仍是一个巨大的挑战.

3)随机梯度下降算法在每轮迭代过程中计算复杂度较低,但只利用了一阶梯度,忽略了目标函数的二阶信息及曲率,从而限制了实际性能和收敛速度[81].如何结合一阶与二阶方法各自的长处，进一步设计迭代效率俱佳的随机梯度下降算法，是未来值得研究的问题.

4)近年来,研究者们将目光投向非凸的ERM模型,并且提出了一些行之有效的解决方案[82-85],其中具有代表性的策略包括添加动量跳出局部最优解[86]、使用方差缩技术减少梯度方差[87]和添加梯度噪声逃离鞍点[88]等.然而,对于更为一般的非凸、非光滑的优化问题却并未取得太大的突破,目前仅有Prox-SAGA[89]、Prox-SVRG+[90]等算法,但性能并不理想.随机梯度下降算法在非凸、非光滑条件下的策略研究,不仅是当前面临的困局,也是未来最具有应用价值的研究方向.

5)对于非凸的优化问题,梯度下降法通常存在两个缺陷:易于陷入局部最优、无法逃离鞍点.而演化计算/智能计算无需计算梯度和确定步长,且往往具有较好的全局收敛性.如何将随机梯度下降算法与演化计算/智能计算方法相结合,将是一个非常值得关注的研究方向.