因子与聚类<br/>——基于十项全能运动员的实证研究

因子与聚类
——基于十项全能运动员的实证研究

2021-11-13张伟，陈鹏

体育科技文献通报 2021年11期

张伟，陈鹏

前言

十项全能被称为“田径之王”，其发展水平是评价一个国家男子田径水平的重要指标；［1］查看我国的田径发展史可发现，在十项全能中，超过8000分大关的仅齐海峰1人，达到国际健将也只有齐海峰1人，而他的最佳成绩与亚洲纪录相差435分，与世界纪录相差多达836分；［2］查看国际田联中国区十项全能运动员高分成绩表可发现，名单中仅有齐海峰1人次，而日本有2人次，俄罗斯有21人次，美国则多达42人次。［3］

卢刚等的研究表明，奥运会十项全能运动员速度因子居首，力量因子、耐力因子、技术因子分列二、三、四位，力量型选手最多，速度型选手更容易取得好成绩，并指出“速度为先导，力量是推进整体的原动力”的理念；孙红炜等的研究表明，世界优秀十项全能运动员总成绩与跳跃项目的关联性最大，以跳跃为主导训练，对促进速度类与投掷类的速度与爆发力有重要作用。

本研究以国际田联的世界优秀十项全能运动员为调查对象，以运动员的成绩特征为研究对象，分别从R型因子分析和R型聚类分析的角度出发，对变量进行分类、解释，以期为我国十项全能的发展提供意见和建议。

1 研究对象与方法

1.1 研究对象

以世界优秀男子十项全能运动员的成绩特征为研究对象，调查数据来源于国际田联官方网站，总共包括101名世界优秀男子十项全能运动员的成绩，总分位于8290－9126之间。（齐海峰的十项全能最佳成绩为8290分，选取的运动员要求十项全能最佳成绩≥8290分，由于未知原因，有5位运动员单项比赛成绩缺失，此5位运动员的成绩作废。）

为方便本研究的数据处理，将十项全能的十个变量进行定义，记为：A1（100m），A2（跳远），A3（铅球），A4（跳高），A5（400m），A6（110m栏），A7（铁饼），A8（撑竿跳高），A9（标枪），A10（1500m）。

1.2 研究方法

1.2.1 文献资料法

本研究参考的有个人文献、官方文献及大众传播媒介等，其中个人文献包括运动员的训练日记，官方文献包括国际田联官方网站运动员的参赛成绩，大众传播媒介包括网络、报刊、书籍等，网络文献主要来源于中国知网、谷歌学术，报刊、书籍主要来源于北京体育大学图书馆，查阅到与本研究相关的论文及图书若干，丰富的理论资源和可靠的数据是本文撰写的重要依据。

1.2.2 专家访谈法

通过访谈相关专家，加深对十项全能的认识。访谈对象选取时采用立意抽样，是根据研究目的选取较有代表性的样本。访谈对象主要包括山东师范大学、北京体育大学田径队教练及田径教研室教师，山东省、江苏省、广东省、天津市等省市田径运动管理中心教练。

1.2.3 数理统计法

主要是运用SPSS21.0对运动员的成绩进行R型因子分析、R型聚类分析及其他统计分析。

2 结果与分析

2.1 假设检验

Kaiser曾研究指出，对于一组数据是否适合进行因子分析，可采用KMO取样适合度检验，这一检验是比较变量间相关与偏相关系数平方和的指标，如果相关系数绝对值大，偏相关系数绝对值小，说明变量间的高相关可能受第三变量的影响，即有存在公因子的可能，可以进行因子分析，反之则不适合进行因子分析。由KMO的计算公式可知，其取值在0－1之间，变量间的相关系数平方和越大，KMO值越趋近于1，即表明变量间相关性高而偏相关性低，适合进行因子分析；变量间的相关系数平方和越小，KMO值越趋近于0，即表明变量间的相关性低而偏相关高，不适合进行因子分析。通常将KMO＝0.6看作一个分界点，随着KMO值的升高，适合进行因子分析的条件增强，随着KMO值的降低，适合进行因子分析的条件减弱，且当KMO＜0.5时，表示极不适合进行因子分析。［4］

其次也可采用巴雷特检验，它是用来检验变量间的相关性，是以原变量的系数矩阵为基础，检验实际相关矩阵与假设单位之间的差异，若存在显著性差异，表明适合作因子分析，否则不适合。

表1 KMO和巴雷特检验

由上表可知，本研究选取数据的KMO度量为0.597，介于0.5与0.6之间，更接近于0.6，虽然进行因子分析的条件不是很强，但可接受；巴雷特检验达到极其显著水平，因此可进行因子分析。

2.2 变量分析

2.2.1 R型因子分析

因子分析，是指在若干个指标中，找出具有支配多个观测量的公因子的方法，这一方法可更快地把握事物的特点和本质，并简化数据。在因子分析中，提取出的公因子应最大限度地概括、解释原有变量，以便达到揭示事物本质及降维的目的，最终实现数据简化。在十项全能中，原始观测量包含十个项目，是可观测的外显变量，而抽象出的公因子则是不可观测的潜在变量，这种公因子的出现主要依赖于十个项目之间的相互关系，它一种抽象的变量。

在确定因子数时，可观测的特性有：因子的特征值，特征值越大，因子的解释力越大，反之则越小，通常将特征值大于1视为一种标准，而小于1的不作为公因子，因为经过标准化后的变量方差为1，如果特征值小于1，表明该因子的解释力甚至小于一个原变量，但要注意的是，不能为了特征值而把实际中相关性并不强的归为一类；原始变量的方差累积解释率，通常将达到80%看作一种标准，但这不绝对，也可根据具体问题和要求进行调整；其他考虑的因素有公因子方差、碎石图拐点、研究目的、理论假设、研究经验等。

表2 旋转成分矩阵

以往研究中，尽管不同的专家对十项全能的归类各不相同，但他们都有一个共同点，即提取的因子数都为4，这是基于特征值的角度出发，选择特征值大于1的公因子而排除特征值小于1的公因子，是一种常用的提取公因子的方法，他们为后续研究提供了借鉴，也在一定程度上指导着实践的进行。沿袭前人研究中提取4个公因子的观点，由上表可发现（基于特征值大于1，旋转成分矩阵中删除小于0.4的载荷），第1因子在变量A1、A2、A5、A6上有较高载荷，第2因子在变量A3、A7上有较高载荷，第3因子在变量A2、A4、A10上有较高载荷，第4因子在变量A5、A8、A9、A10上有较高载荷，在各个因子内部，区分度较强的是第1、2因子，这也与前人的研究基本一致，第3、4因子分别包含3、4个变量，通过常识我们也可辨别，变量之间难以提取公因子，因此，提取4个公因子并不能满足实际的需要，需要重新归类。这也体现出单一特征值的劣势，在对十项全能进行归类时，不能只看特征值，应多方面综合考虑。

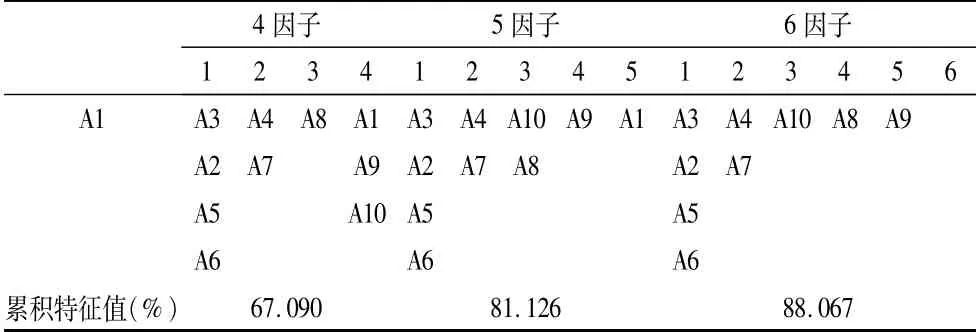
表3 不同因子数特征

在实际操作中，公因子的抽取数量是一个需要考虑的问题。通常情况下，公因子越多，模型的解释能力越强；公因子越少，模型的遗失信息越多，解释能力就越弱，但如果因子数过多，则无法达到简化变量的目的。因此，在抽取因子数量时，要平衡模型解释量与因子结构之间的关系。本研究中，分别选取因子数为5、6，并与4因子数进行比较，以获取最合适的因子数，当因子数为5、6时，因子累积方差的数值完全一样，但与4因子数不同，且根据实际情况看，多于6个因子明显不合理。由上表可知，当提取公因子为4时，累积特征值是67.090%，当提取公因子为5、6时，累积特征值均超过80%，公因子为4时，累积特征值偏小。

表4 公因子方差

变量共同度是指提取某一数量的公因子时，每个变量能被所有公因子解释的比例，共同度越高，表示提取的公因子越合理，通常认为共同度大于0.8是比较理想的，大于0.6是可接受的，由上表可知，当因子数为4时，A8、A9提取的共同度低于0.6，当因子数为5时，A4提取的共同度低于0.6，当因子数为6时，所有变量提取的共同度均高于0.6。

2.2.2 R型聚类分析

聚类得出的结果，应满足以下要求：第一，类内差距要明显小于类间差距；第二，分类要有实际意义；第三，在使用不同方法分类时，应有更多相同的类。对变量进行分类，是为了把握其内部结构，以更好地认识变量，因变量有其自身规律和发展逻辑，所以在分类时不应盲目，无论是采用因子分析还是聚类分析，都要付诸于实践，让实践检验分类正确与否。

表5 聚类表

选择首先出现在聚类过程中的变量，由上表可知，首先，A3与A7聚为一类，表明二者的相似性最大，都是力量主导型，这与R型因子分析相符；其次，A1与A5聚为一类，表明二者的相似性次之，都是速度能力占主导，也与R型因子分析相符；再次，A2与A6聚为一类，表明二者也有较高相似性，对速度能力、力量及技术都有较高要求，由于不再是单纯地跑，而是将跑（速度能力）与跳（力量、技术）进行结合，速度能力最重要，也与R型因子分析相符；最后，A4与A8聚为一类，二者对核心力量及技术要求较高。以上聚类证明了两两变量之间的相似性强弱，其中既有与R型因子分析相同的地方，也有存在差异的地方，这表明即使完全相同的数据，不同统计的结果也会有所不同，这就要理论与实际相结合，辩证促进项目的发展。

2.2.3 相关性分析

表6 单项最佳相关性

观察上表可知，在单项之间，当达极其显著性水平时，存在相关的有A1与A2（r1）、A1与A5（r2）、A1与A6（r3）、A2与A4（r4）、A2与A5（r5）、A2与A6（r6）、A3与A7（r7）、A5与A6（r8），相关性排序为r7＞r3＞r1＞r2＞r6＞r8＞r5＞r4。相关性最强的是A3与A7（p＜.01），表明A3与A7具有潜在公因子的可能性最大，A1、A2、A5、A6四个单项之间互为相关（p＜.01），表明四者之间具有潜在公因子的可能性次之，显著性最弱的是A2与A4（p＜.01），表明A2与A4具有潜在公因子的可能性最低，A2同时与A1、A5、A6及A4存在相关（p＜.01），但与前者各个项目的相关性更强，实际经验也告诉我们，A2与前者的相似度更大，因此，更倾向于将A2与前者归为一类；当达显著性水平时，存在相关性的有A1与A3（t1）、A1与A7（t2）、A1与A10（t3）、A2与A8（t4）、A2与A10（t5）、A3与A9（t6）、A5与A9（t7），相关性排序为t3＞t4＞t6＞t7＞t1＞t5＞t2，除去前面已确定的A3、A7组及A1、A2、A5、A6组，表明A3、A7、A9及A1、A2、A5、A6、A10也具有潜在公因子的可能，但是可能性较低。

依据相关性分析，结合R型因子分析与R型聚类分析，本研究得出以下归类：A1、A2、A5、A6为第1类，A3、A7为第2类，A4、A8为第3类，A10为第4类，A9为第5类。应注意的是，在对十项全能进行因子分析时，如果数据满足适合度检验，公因子应由特征值、方差累积解释率及公因子方差等共同决定，而不能只取决于特征值，否则会出现与实际不相符的分类。

2.3 贡献率分析

表7 单项最佳贡献率

续表7 单项最佳贡献率

十项全能中单项理论贡献率排序为A2＞A6＞A8＞A4＞A5＞A1＞A9＞A3＞A7＞A10，其中A2的贡献率最大，A10的贡献率最低。如果仅按贡献率来看，应重点发展A2单项，再结合项目归类，应重点发展第1类；第3类的单项贡献率次之，第2类的单项贡献率排名靠后，但第2类项目属于力量主导型，力量素质是基础身体素质，提高力量素质，对提升整体身体素质及技战术水平都有积极的促进作用，因此，不能因为第2类的贡献率低而有所轻视。

2.4 讨论

在R型因子分析中，当因子数为5时，第3因子在变量A2、A4、A8上有较高载荷，当因子数为6时，第3因子在变量A2、A4上有较高载荷，在相关性分析中，A2、A4的相关性r4＝0.260（p＜.01），实际经验告诉我们，A2与A4具有较强相关性，是因为二者对下肢爆发力及核心力量有较高要求；A1、A3存在相关性t1＝0.179（p＜.05），A1、A7存在相关性t2＝0.176（p＜.05），是因力速度能力的提高对力量素质有较高要求；A1、A10存在相关性t3＝0.249（p＜.05），A2、A10存在相关性t5＝0.177（p＜.05），是因为A10对速度能力已有了较高的要求；在R型聚类分析中，第2阶（A1、A5）先是与第4阶（A4、A8）合并，在相关性分析中，A2、A8存在相关性t4＝0.220（p＜.05），A3、A9存在相关性t6＝0.196（p＜.05），A5、A9存在相关性0.180（p＜.05），以上数据表明，十项全能各个项目之间是相互影响与制约的，在训练中要全面统筹，均衡发展，才能做到有的放矢。