冷却塔群塔风致干扰脉动风压频谱特性与相关性
2021-11-12陈翰林葛耀君
陈翰林,赵 林,张 栋,刘 鑫,任 翔,葛耀君
(1. 同济大学土木工程防灾国家重点实验室,上海 200092;2. 中南安全环境技术研究院股份有限公司,武汉 430070;3. 同济大学桥梁结构抗风技术交通运输行业重点实验室,上海 200092;4. 中国电力工程顾问集团中南电力设计院有限公司,武汉 430071;5. 深圳中广核工程设计有限公司,深圳 518100)
大型冷却塔是火力发电厂与核电站大量使用的用于冷却的工业建筑物,其多为双曲线型混凝土薄壳结构或钢结构,具有结构质量轻、刚度小、阻尼小、自振频率低等特点。近些年随着电力需求的扩张,冷却塔建设呈现“更高、更大”的发展趋势。一方面,塔筒结构进一步柔性化,自振频率持续降低,结构更容易在低风速下产生振动,其结构特点已经超出了规范[1-2]的应用限制;另一方面,近些年冷却塔建设规模从双塔、四塔向六塔、八塔逐渐发展,群塔组合对单个冷却塔的流场条件形成了干扰,相关文献[3 - 4]指出干扰条件下冷却塔的风荷载效应更加突出,开展群塔干扰的研究工作显得尤为重要。
1965 年英国渡桥电厂冷却塔群(八塔组合)风毁事故[3]掀起了冷却塔的群塔干扰效应问题的研究浪潮。国际上,Flaga[5]研究了干扰风荷载计算方法;Orlando[6]研究了双塔干扰条件塔筒表面的平均风压分布模式;Niemann 等[3]以双塔干扰为基础研究了内力干扰系数。在国内,1980 年以来,顾志福等[7-9]研究了两塔和三塔干扰条件下的塔筒表面风压分布;赵林等[10-12]研究阐明了干扰条件下的风荷载模式与干扰准则;柯世堂等[13-14]研究了不同群塔布置条件下的静动力荷载干扰效应;沈国辉等[15-16]基于双塔以及三塔布置情况研究了荷载与内力的干扰变化规律;张军锋等[17-19]开展了群塔干扰条件下的冷却塔整体风荷载变化规律的研究;赵林等[11]和于淼[20]基于配筋包络的干扰研究思路分别针对六塔组合与八塔组合的冷却塔群体建筑进行了的研究;赵林等[21]和程霄翔等[22]基于荷载分布模式开发了冷却塔优化选型算法;周良茂等[23]现场实测结果表明双塔布置条件下前塔的干扰会对后塔表面的脉动风压产生显著放大。赵林等[24]基于冷却塔八塔组合风洞试验定量研究了干扰条件下脉动风压的分布模式。鉴于干扰对脉动风荷载的显著影响,针对脉动风压的研究近年来越来越受到相关学者的重视,表1 列举了主要学者代表性工作进展。
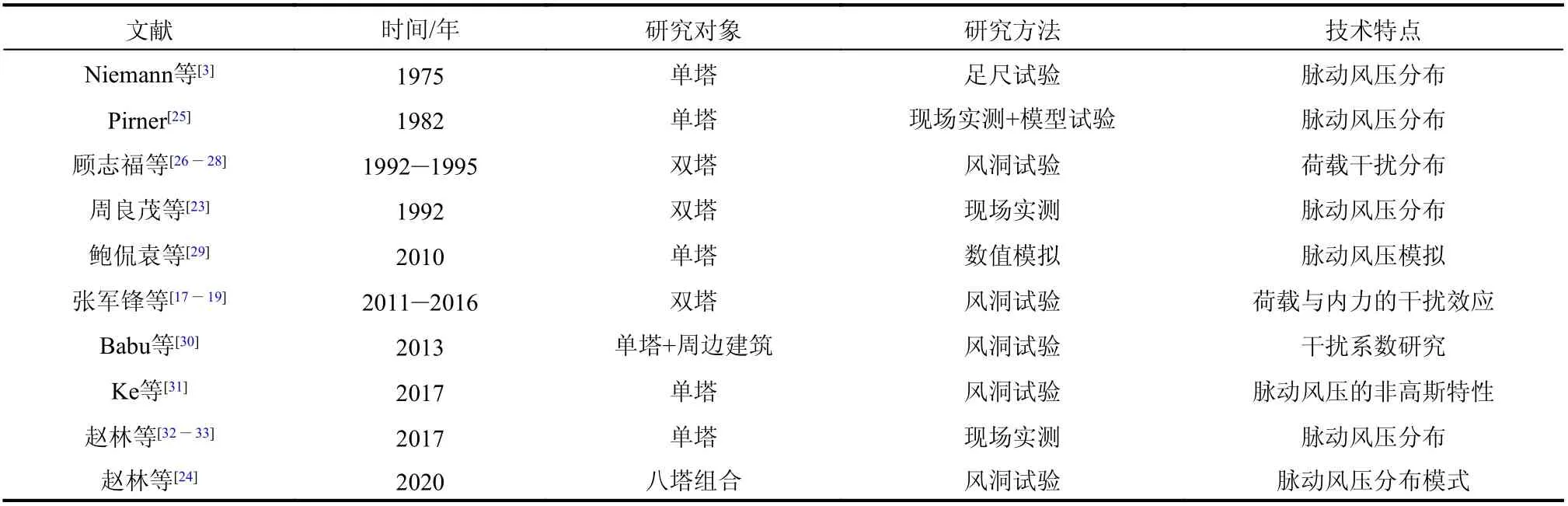
表1 冷却塔脉动风压研究历程Table 1 Research history about aerodynamic pulsation loads of cooling towers
传统的对冷却塔的脉动风荷载干扰效应的主要是从脉动风压的分布以及干扰系数入手,而针对脉动风压统计特性如脉动风压相关性以及干扰对脉动风压在频域分布的影响研究较少,脉动风压的相关性和频域特性对结构的动力作用联系密切,对于具有较低固有频率的冷却塔而言,其研究价值可见一斑。有鉴于此,开展了冷却塔风致干扰脉动风压特性的研究:以某一在建的八塔组合冷却塔项目为背景,选取常见的矩形布置方式,在风洞进行刚体模型测压试验,基于模型表面的风压分布时程研究不同测点间的风压相关性,并在频域分析研究了干扰对塔筒表面关键点风压功率谱和环向合力功率谱的影响特性。
1 同步测压风洞试验
依托冷却塔工程为八塔组合矩形布置,图1列举了塔筒的实际几何外形与尺寸参数。测压风洞试验是在同济大学TJ-3 风洞中完成的,该风洞风速范围为1 m/s~17.6 m/s,连续可调,流场不均匀性指标δU/U≤1.9%,紊流度Iu≤2.0%,来流竖向倾角Δα≤±0.2°,水平偏角Δβ≤±0.1°。
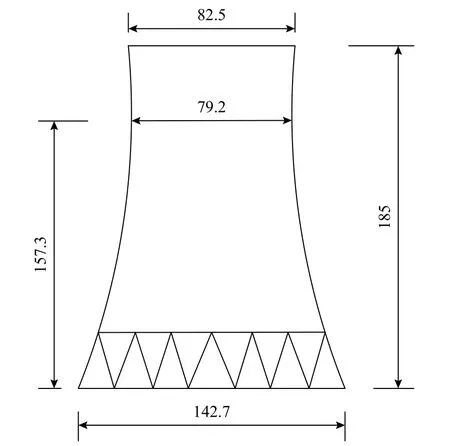
图1 冷却塔塔筒实际尺寸参数 /mFig. 1 Actual size parameters of cooling tower
试验模型采用双层有机玻璃制作以保证足够的刚度,模型缩尺比为1∶300。单个结构迎风面积约为0.18 m2,八塔群塔组合后阻塞率约为2.4%。试验模型与实际冷却塔的雷诺数差异通过在模型表面贴纸带加以补偿,整个塔筒外表面环向共粘贴36 条子午向通长纸带,雷诺数效应模拟结果满足规范要求[24]。测点沿着外表面布置12 层,每层36 个测点沿着环向均匀布置,图2 展示了测点的布置示意图。试验采用同步扫描测压技术,测压信号采样频率为300 Hz,每个测点采样时长为60 s。

图2 模型测压孔布置示意图Fig. 2 Schematic diagram of model pressure tap layout
试验中八塔组合采用矩形布置,图3 展示了八塔在风洞中的布置方式,数字为各塔的编号,其中相邻塔筒之间的距离为塔筒底部直径的1.5 倍。图3 中冷却塔群正对的方向为风向角的正方向,以其为0°方向,沿着来流顺时针方向为正角度的方向。风向角沿着环向从0°~360°变化,每间隔22.5°进行一次测压试验。为了减少试验的工作量,根据矩形布置形式的对称性,只需针对图3中1 号塔和2 号塔进行测压试验。共获得了1 号塔和2 号塔的各16 个风向角下塔筒表面的风压时程。
试验模拟B 类紊流场,模拟方式采取粗糙元和尖劈实现,其布置情况如图3 所示。试验风场的顺风向和横风向的风速功率谱函数,与规范建议的实测风谱拟合对比良好[24]。

图3 群塔组合布置形式Fig. 3 Grouped-tower arrangement
2 干扰对脉动风压相关性的影响
干扰会影响塔筒周围的流场结构,进而影响塔筒表面脉动风压之间的相关性。以1 号塔、2 号塔为例,分析不同风向角的来流对冷却塔表面喉部位置的环向相邻测点脉动风压之间的相关性,以及测点风压与塔筒整体合力系数之间的相关性,并与单塔进行比较,其结果见于图4。阻力(风压环向合力沿着顺风向的分力)和升力(风压环向合力沿着横风向的分力)系数定义如下:

图4 喉部不同角度位置的测点脉动风压与阻力系数的相关系数Fig. 4 Correlation coefficient between fluctuating wind pressure and overall drag force at different angles in throat

式中:x与y分别为数据时程序列,如风压时程或者合力时程等;E(x)与E(y)分别为x与y的期望值; σx与 σy分别为x与y的标准差。若x(i)与x(i+1)分别表示测点i与测点i+1 的风压时程,R(x(i),x(i+1))则表示相邻测点i与测点i+1 的风压相关性。
图4 比较了单塔以及所有试验风向角下1 号塔、2 号塔表面喉部位置的脉动风压与整体阻力系数的相关性,图示过程不区分风向角差异以方便比较。图4 中箭头表示干扰作用的趋势变化方向,箭头向上表示增大正相关性或者减小负相关性;箭头向下表示减少正相关性或者增大负相关性。测点风压与整体阻力的相关性沿着环向明显分成两个区域,即A1 区与A2 区。A1 区范围是迎风点两侧0°~45°,A2 区是45°~315°区域。干扰后处于A1 区的测点脉动风压与整体阻力的相关性减弱,A2 区测点的脉动风压与整体阻力的相关性增强,大部分风向角下A2 区测点与阻力系数之间的相关性由负转正。表明干扰会减小迎风区风压对阻力系数的贡献,增强背风区风压对整体阻力系数的贡献。
群塔之间的相互干扰会直接影响塔筒表面相邻测点之间的风压相关性,从图5 看这种调整作用沿着塔筒的环向可分为三个区域,即B1 区、B2 区、B3 区。B1 区的范围是迎风点两侧0°~70°,B2 区的范围是迎风点两侧70°~130°,B3 区的范围是迎风点两侧130°~180°。在B1 区,干扰会降低相邻测点之间的风压相关性。干扰在B2 区的作用比B1 区复杂,部分测点之间的相关性降低,但大部分测点之间的相关性受干扰影响变大。B2 区干扰引起的相关性波动比B1 区剧烈,这可能归因于B2 区处于塔筒表面的漩涡区[34]。受漩涡脱落的影响,该区的风压变化比在B1 区剧烈,而干扰引起塔筒周围流场中的紊流成分增加进一步增加了漩涡区风压的波动程度,因而出现B2 区的相关系数的大幅度波动。B3 区相邻点的脉动风压相关性受干扰影响后呈降低趋势,源于干扰后尾流区紊流成分增加导致测点间相关性减弱。
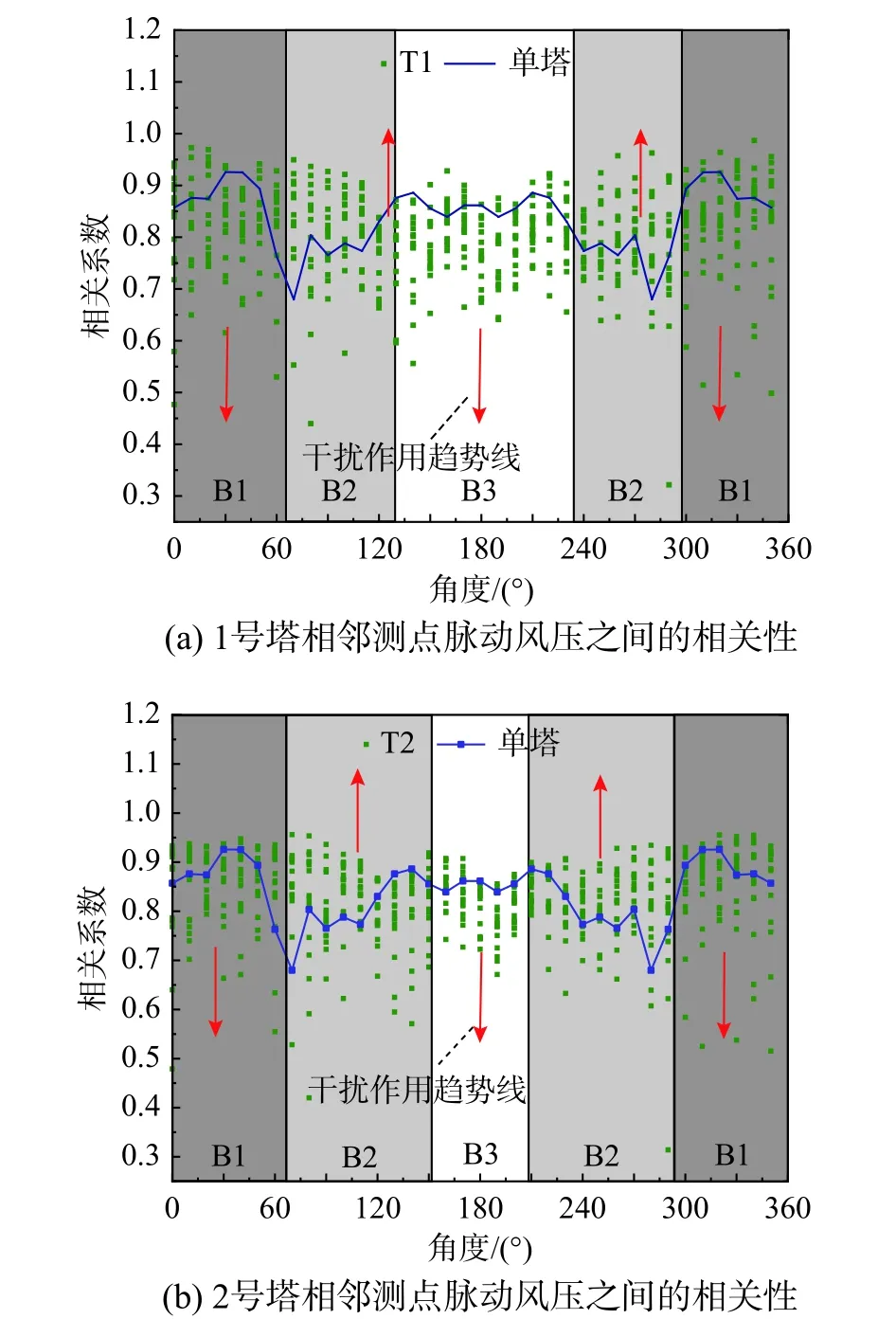
图5 喉部不同角度位置的相邻测点之间的脉动风压相关系数Fig. 5 Correlation coefficient of fluctuating wind pressure between adjacent points at different angles in throat
3 干扰对脉动风压功率谱的作用
3.1 干扰对特定点的风压功率谱的影响
脉动风荷载的功率谱成分决定了其对结构的动力作用,自然风的频率较低,其与高耸结构的低阶自振频率接近,因而会引起结构的振动。冷却塔的风振效应的强弱受风谱成分的直接影响。干扰除了会影响脉动风压的静力分布外,也会影响其功率谱函数分布特征,从而间接影响结构的风振效应。本文以结构关键特定点的风压功率谱以及合力功率谱为探讨对象,结合不同来流方向分析干扰对结构特定点风压与合力的影响规律。
选择沿着喉部位置环向分布的0°、90°和180°三个测点的风压谱为研究对象,代表了处于迎风区、负压区和尾流区的几种风压特性[35-36]。图6 和图7 分别展示了1 号塔与2 号塔的喉部位置0°、90°和180°三个测点在0°~337.5°共16 个风向角的风压谱。与单塔对应测点的风压谱相比,1 号塔与2 号塔的0°与180°测点的风压谱随着风向角的变化在单塔风压谱附近波动,在一些风向角下,测点低频段的风压谱密度低于单塔。根据归一化原则,相对应在频率变高的时候,风压谱密度将高于单塔;在另一些风向角下,测点低频段的风压谱密度高于单塔,相对应在频率变高的时候,风压谱密度将低于单塔。整体来看随着风向角的变化,0°测点与180°测点处的风压谱在单塔风压谱附近波动且幅度不大,表明风向角对0°测点与180°测点处的风压谱影响较小。与之具有差异的是,90°测点的风压谱呈现趋势性的干扰规律:在归一化频率1 以下,大多数风向角情况测点的风压功率谱比单塔对应测点的功率谱密度低;当归一化频率高于1 时,测点的风压功率谱密度高于单塔对应频段的功率谱密度。表明干扰会降低负压区脉动风压低频段的风压能量,提高其高频段的能量,其作用差异的频段分界线在归一化频率1 左右。
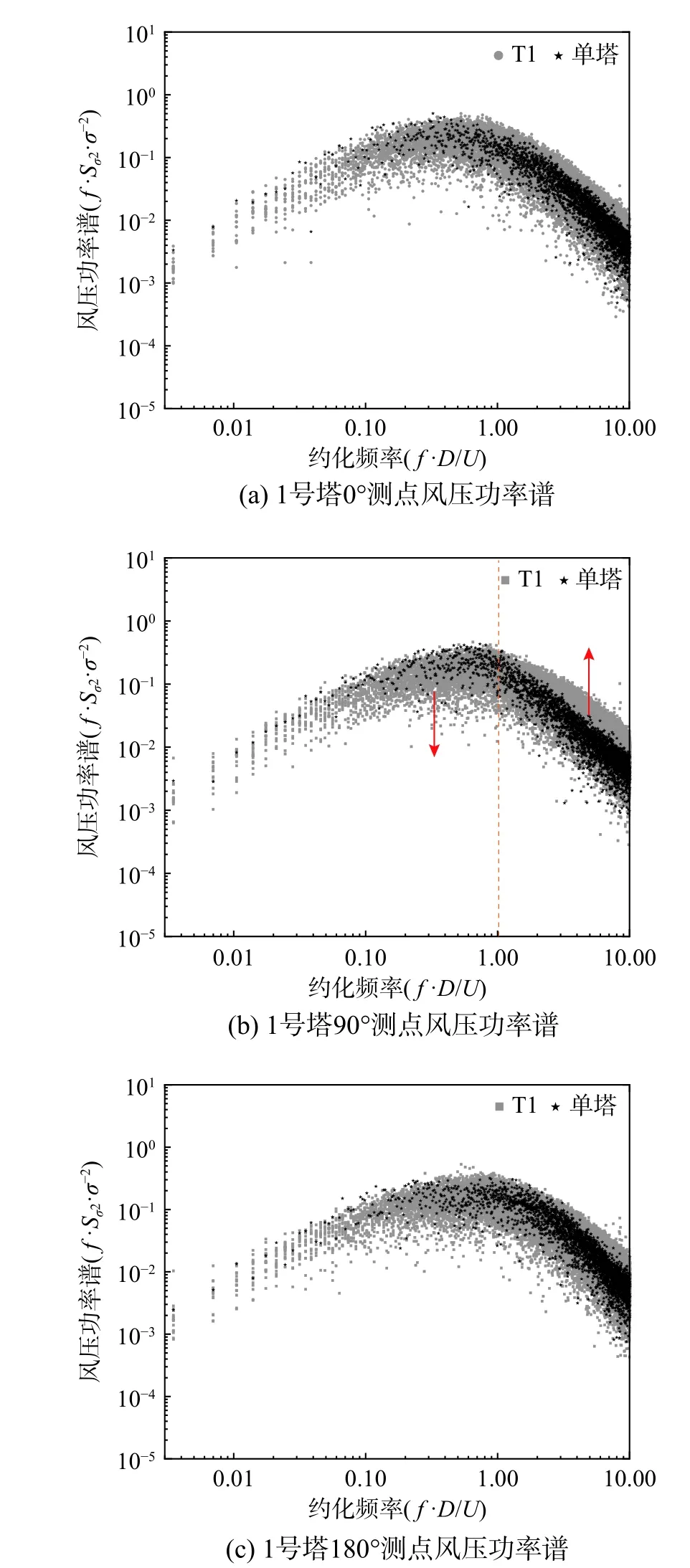
图6 喉部不同位置测点风压功率谱(1 号塔)Fig. 6 Wind pressure power spectrum of measured points at different positions of throat (Tower 1)

图7 喉部不同位置测点风压功率谱(2 号塔)Fig. 7 Wind pressure power spectrum of measured points at different positions of throat (Tower 2)

拟合针对塔筒喉部位置特定测定进行,在拟合过程中不区分塔筒的在群塔中的位置以及风向角的变化,将试验的1 号塔与2 号塔的共计32 种试验工况结合起来考虑,对0°、90°和180°三个位置的测点的风压功率谱进行拟合。拟合结果如图8所示。拟合曲线的上下限参数如表2 所示。

表2 塔筒合力功率谱拟合公式参数Table 2 Parameters of the formula for fitting the resultant spectrum of the tower
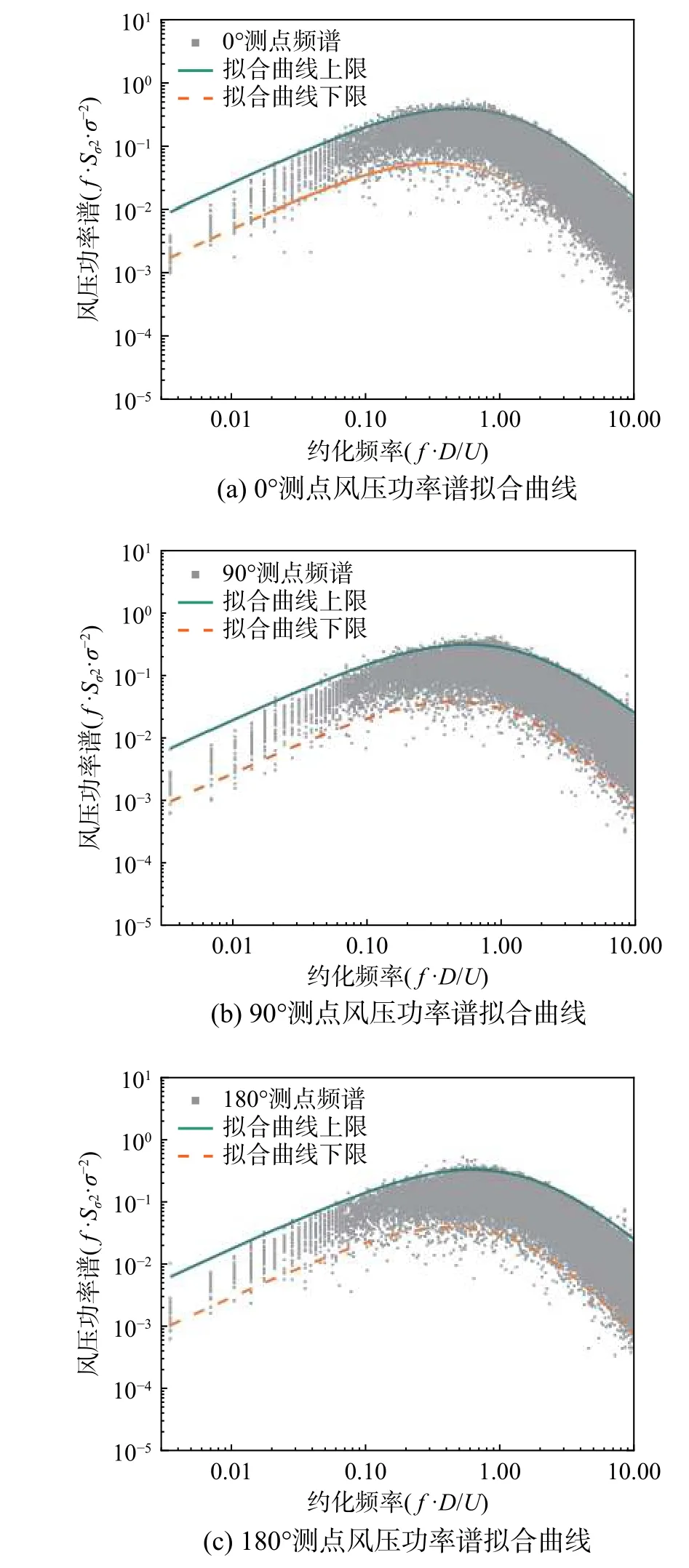
图8 不同测点的风压功率谱曲线拟合Fig. 8 Curve fitting of wind pressure power spectrum at different measured points
3.2 干扰对合力功率谱的影响
根据刚性模型测压试验可以得到塔筒表面的压力分布,根据式(1)和式(2)可以得到塔筒的阻力与升力时程,对阻力与升力时程作傅里叶变换获得功率谱函数,选2 号塔为研究对象,在不同风向角下比较2 号塔的合力功率谱与单塔合力功率谱,其对比结果如图9 和图10 所示,其中黑色的数据点代表单塔的合力功率谱,灰色的数据点代表试验的16 个风向角下2 号塔合力的功率谱,为分析干扰的整体作用规律,灰色数据点不区分具体的风向角。1 号塔、2 号塔的对比结果均表明:干扰条件下结构的阻力与升力功率谱相比单塔均发生明显的偏移,这种偏移变化可以分为三个区域:C1 区、C2 区和C3 区;将升力功率谱密度三个区命名为D1 区、D2 区和D3 区。对于阻力和升力,三个区域之间的界线并不相同但较为接近。对于阻力功率谱,干扰条件下C1 区(0~0.2)归一化频率范围的阻力成分减少,C2 区(0.2~1.1)归一化频率范围的阻力成分增加,C3 区(1.1~10)归一化频率范围的阻力成分减少;对于升力功率谱,干扰条件下D1 区(0~0.2)归一化频率范围的升力成分增加,D2 区(0.2~1.1)归一化频率范围的升力成分减少,D3 区(1.1~10)归一化频率范围的升力成分增加。目标冷却塔前十阶归一化频率集中在1.05~1.56。朱佳宁等[34]的研究也指出,250 m级冷却塔的前100 阶频率较集中,按照目标冷却塔换算,归一化频率在0.72~3.6,表明对结构动力作用较大的区间为C3 区与D3 区。该区域升力功率谱成分干扰后增加,推断干扰条件下的升力将会引起受扰塔产生更不利的风振效应,而阻力系数由于在结构敏感频率成分区间的成分受干扰后减少,其对结构动力作用不会恶化。综合以上分析,干扰会引起处于结构敏感区域的升力功率谱成分增加,阻力功率谱成分减弱。

图9 不同风向角下干扰对阻力功率谱的影响趋势Fig. 9 Interference effect on drag force spectrum at different wind direction angle
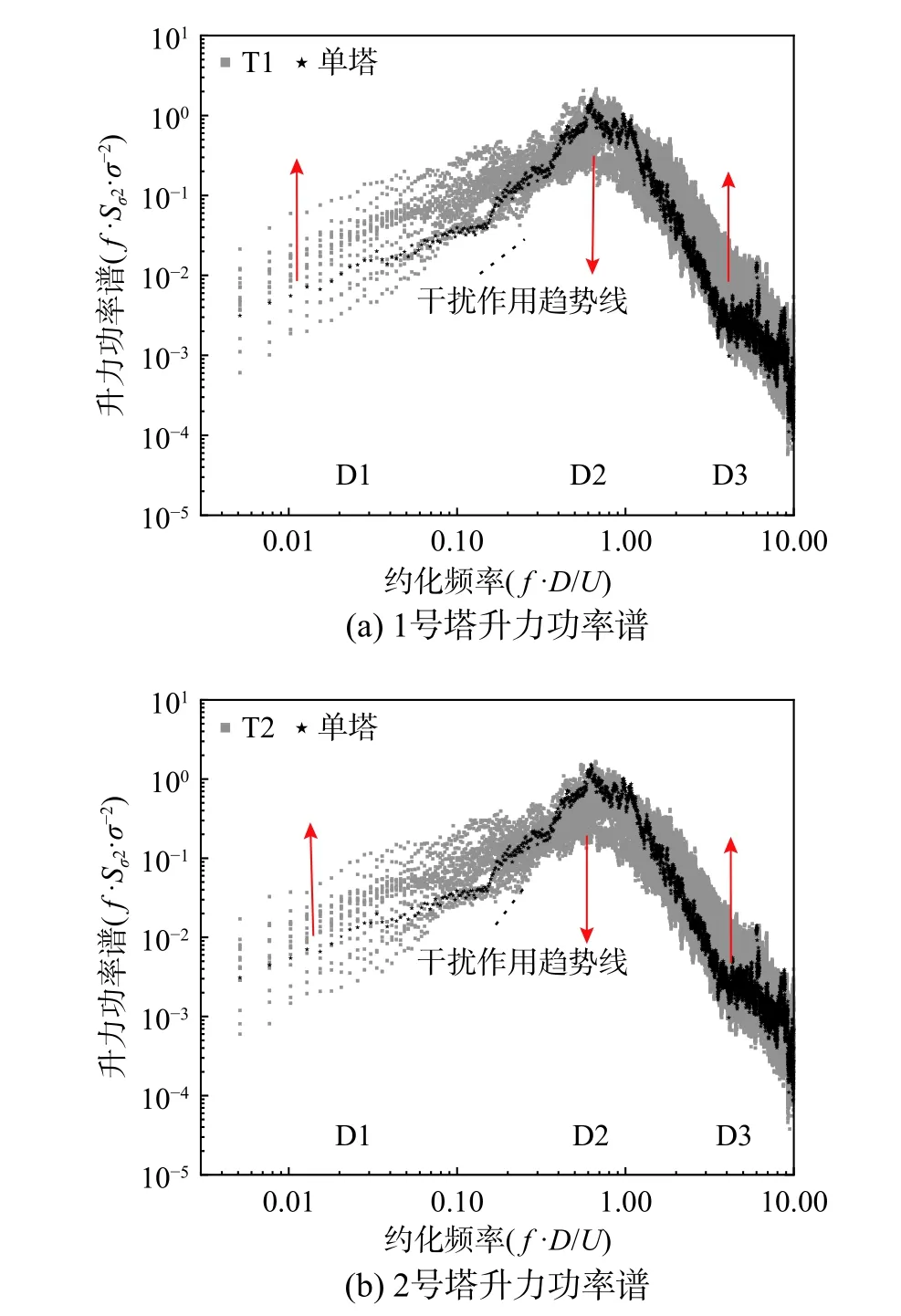
图10 不同风向角下干扰对升力功率谱的影响趋势Fig. 10 Interference effect on lift force spectrum at different wind direction angle
为了定量反映合力功率谱的干扰效应,尝试对干扰后的合力功率谱进行拟合,采用如式(5)所示的公式进行拟合,其拟合效果如图11 所示。干扰后阻力功率谱以及升力功率谱随着风向角不同呈现带状分布,表3 分别给出带状分布的上限与下限拟合曲线的参数取值范围。
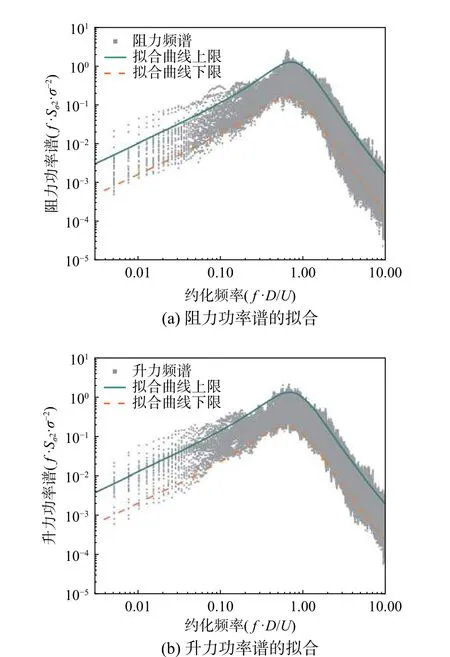
图11 合力功率谱的曲线拟合Fig. 11 Curve fitting of resultant spectrum


表3 塔筒合力功率谱拟合公式参数Table 3 Parameters of the formula for fitting the frequency spectrum of the tower

4 结论
基于八塔矩形布置条件下的风洞试验,进行了脉动风压相关性与风压功率谱的研究工作:对比了不同风向角下相邻测点之间的相关性以及环向测点与阻力的相关性;从频域角度研究了干扰对塔筒表面关键特定点的风压功率谱以及合力功率谱的影响。通过考虑不同风向角工况的对比,获取了脉动风荷载的基本干扰特性,得到以下基本结论:
(1)干扰会降低迎风侧测点风压与整体阻力的相关性,增加背风侧测点风压与整体阻力相关性。测点间的风压相关性在迎风侧与背风侧减小,侧风区增大。
(2)干扰对迎风侧测点与背风侧测点的风压功率谱影响较小,会降低负压区的测点低频段的功率谱密度,提高高频段的功率谱密度。
(3)干扰会引起结构升力与阻力功率谱成分偏离单塔,且变化趋势分为三个区域。处于结构敏感区域的升力功率谱成分增加,阻力功率谱成分减弱。
(4)给出了喉部位置环向特定点功率谱以及合力功率谱的拟合关系式,其上下限值包络了合力功率谱的带状分布。
(5)本文仅针对八塔矩形布置条件下的脉动风压频谱特性做出了分析,对于变化塔筒数量以及组合形式引起的脉动风压的频谱特性的变化,是否有类似结论,仍需要进一步研究。
