基于改进蝗虫算法优化长短时记忆神经网络的多参数瓦斯浓度预测模型研究*

2021-11-12王雨虹王淑月王志中任日昕

传感技术学报 2021年9期

王雨虹，王淑月，王志中，任日昕

(辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105)

瓦斯浓度是衡量煤矿瓦斯危害程度的一个重要指标，瓦斯浓度超限与瓦斯爆炸、井下人员窒息和煤与瓦斯突出等煤矿恶性事件息息相关[1－3]。井下环境复杂，瓦斯浓度变化不是简单的静态过程，与其影响因素之间有着高度复杂的非线性关系。通过对煤矿瓦斯事故的调查和原因分析发现，没有准确掌握瓦斯浓度变化规律是瓦斯事故发生的主要原因之一[4]。因此，精确、高效地预测瓦斯浓度是预防瓦斯事故的重中之重。

迄今为止，很多国内外学者对瓦斯浓度预测做了大量的研究工作，瓦斯浓度预测方法大体可分为统计学模型和机器学习模型两类。统计学模型主要包括时间序列法[5]、模糊预测法[6]、灰色模型法[7]等。这些方法是以历史数据为基础，对于时序性较强的数据有较好地预测精度，但无法同时兼顾瓦斯浓度数据的非线性与时序性的关系。机器学习方法中，支持向量回归机[8](Support Vector Regression，SVR)、神经网络[9－10]等方法在瓦斯浓度预测中研究较多。这些算法提高了瓦斯浓度预测的精度，但模型建立和训练过程中，需要依据经验来人为地设置参数及模型的结构，缺乏对瓦斯浓度时序相关性特征的考虑。

近年来，深度学习以其强大的数据处理能力，在控制领域[11]、语言处理[12]、生物医学[13]等方面得到了迅速发展，众多的深度学习算法也被应用到了瓦斯浓度的预测中。李树刚[14]等人采用循环神经网络(Recurrent Neural Network，RNN)模型，实现了工作面的瓦斯浓度预测。程子均[15]等人把空间相关的先验信息考虑进去，构建了长短时记忆(Long short-term memory，LSTM)的神经网络模型实现了预测。LSTM模型通过多层非线性映射，可以较好地把握多个变量之间不可视化的非线性关系，并且可以考虑到时间序列新旧信息的关联性，逐层学习到大量数据中蕴含的抽象特征。但是，上述模型的超参数一般依据经验而定，设置不准确会导致算法拟合能力不够强，难以达到预期效果。

本文提出一种改进蝗虫优化算法(improved grasshopper optimization algorithm，IGOA)优化LSTM的多参数瓦斯浓度预测模型。首先，对瓦斯多参数时间序列进行相关性分析和小波去噪，得到输入变量；其次，针对GOA算法易陷入局部最优的问题，通过重构线性缩减因子c、引入柯西－高斯混合变异和最优邻域扰动策略联合改进蝗虫优化算法提高其全局寻优能力，并用改进的IGOA优化LSTM的超参数，构建IGOA-LSTM的多参数融合的瓦斯浓度预测模型。实例分析证实，本文所提出的预测模型有更高的准确率。

1 数据预处理

1.1 多变量时间序列的相关性分析

为了更好地满足瓦斯浓度预测的要求，增强预测模型的态势感知能力和外推能力，本文采用Pearson相关系数[16]来描述工作面瓦斯浓度与其影响因素之间的关联程度。它的计算公式如下:

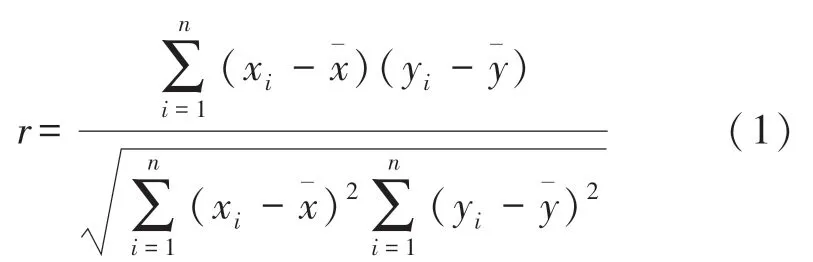
式中:n为样本数，xi、yi分别为两个n维向量x、y的变量值，分别为向量x、y中元素的平均值。

1.2 小波阈值降噪

小波阈值降噪[17]是一种经典的降噪方法，小波阈值去噪一般分为以下三个步骤:

①小波分解。选择合适的小波基和分解层数进行分解，得到小波系数WTf(j，k)。

②阈值处理。通过合适的阈值η和阈值函数，把信号分解为细节分量与近似分量，得到估计小波系数。固定阈值η为:

式中，N为原始信号个数，σ为噪声标准差。

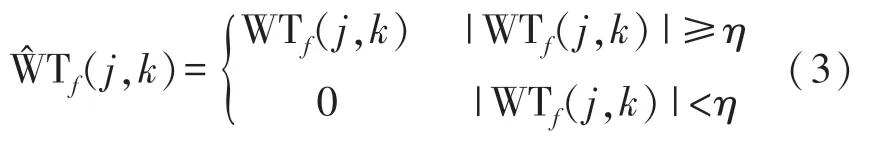
1.3 归一化处理

瓦斯多参数时间序列存在不同的量纲，对原始时间序列x进行归一化处理:

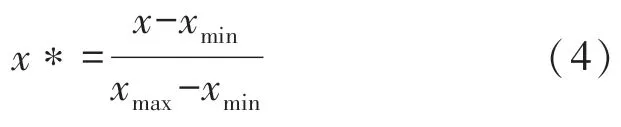
式中，x*为标准化之后的值，xmax，xmin分别为样本数据的最大值和最小值。

2 长短时记忆神经网络

长短时记忆神经网络LSTM[18]是RNN的改进模型，可以高效地分析及处理时序特征的长期依赖关系[19－21]。如图1所示，LSTM分别由遗忘门、输入门、输出门、状态单元组成。A表示上一个元胞，σ为sigmod激活函数。

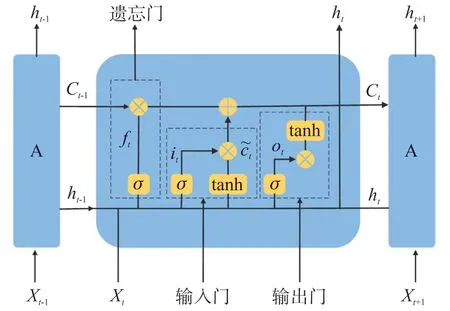
图1 LSTM单元结构示意图

遗忘门:当前时刻细胞单元的输入特征向量Xt与上一时刻的单元状态Ct－1、上一时刻的输出ht－1三者共同作用于细胞状态，并且由sigmod函数产生遗忘门输出值ft，从而选择性地遗忘记忆细胞中的信息。

输入门:输入层通过sigmoid函数和tanh层两部分叠加运算进行值的更新，也就是细胞状态Ct－1更新为Ct。

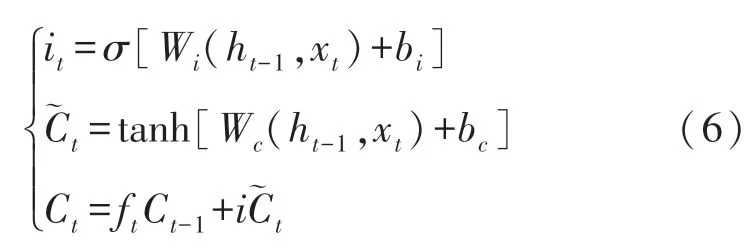
输出门:把sigmoid和tanh函数的输出值相乘得到模型的输出ht。

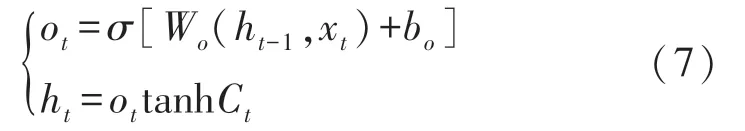
式中，xt为当前时刻的输入信息；W*分别为相应门的连接权重；b*分别为相应门的偏置系数。

3 基于IGOA-LSTM的预测模型

3.1 蝗虫优化算法

蝗虫优化算法[22](GOA)是新型群智能优化算法，该算法模拟了蝗虫的捕食行为，蝗虫群体分为负责全局搜索的成虫和开发某个特定临近区域的幼虫，蝗虫位置模型[23]可表示为

式中，f、l分别为吸引强度参数与吸引尺度参数。依据文献[23]，取f＝0.5，l＝1.5。

c为线性缩减因子，参数c更新模型可表示为:

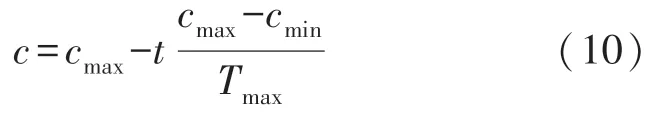
式中:cmax，cmin是参数c的最大值和最小值，Tmax是最大迭代次数，t是当前迭代次数。本文取cmax＝2，cmin＝0。

3.2 改进蝗虫优化算法

3.2.1 重构线性缩减因子c

由传统GOA的寻优过程可以看出，线性缩减因子c影响整个迭代过程的探索和开发能力。由式(10)可知，线性缩减因子c的值整体上是从2线性减小到0，而初期c值下降过快会使蝗虫个体陷入局部最优，后期下降过慢会导致局部探索能力不够。因此，重新构建新函数c(t):

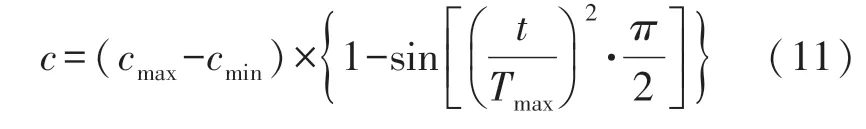
原始的函数c(t)与重新构建的函数c(t)的对比图如图2所示。

由图2可知，重新构建的函数c(t)呈现出非线性递减，在算法搜索前期保持较大值且下降缓慢，可增强算法全局探索的能力，在算法搜索后期具有较小值且下降迅速可以实现对某个区域的局部开发。因此，所提出的非线性缩减因子可以更加高效地平衡全局搜索以及局部探索的能力。

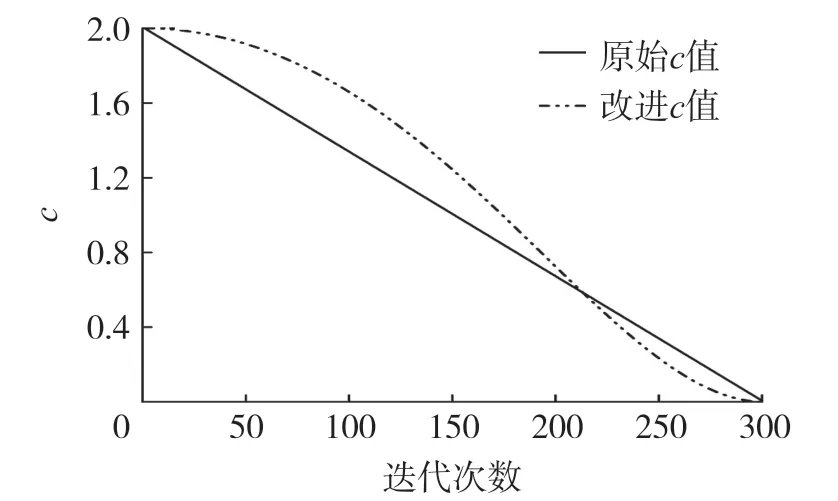
图2 线性缩减因子c的变化

3.2.2 引入柯西－高斯混合变异

由式(8)可知，蝗虫个体在寻找最优位置时，易陷入局部最优，因此在位置更新公式中引入柯西－高斯混合变异。前期成虫进行全局寻优时，引入柯西算子[23]加大成虫搜索步长，以更高的概率快速找到全局最优解，位置更新公式如下:

式中，Xnew(t＋1)是第i只蝗虫在第t＋1代的位置，Xi(t)是第i只蝗虫在第t代的位置，Xbest(t)是第t代最优位置，Xk(t)是第t代的随机位置，Cauchy是柯西算子。

后期幼虫局部开发时引入高斯算子[24]，如图3，加强局部搜索能力，提高收敛速度，位置更新公式如下:

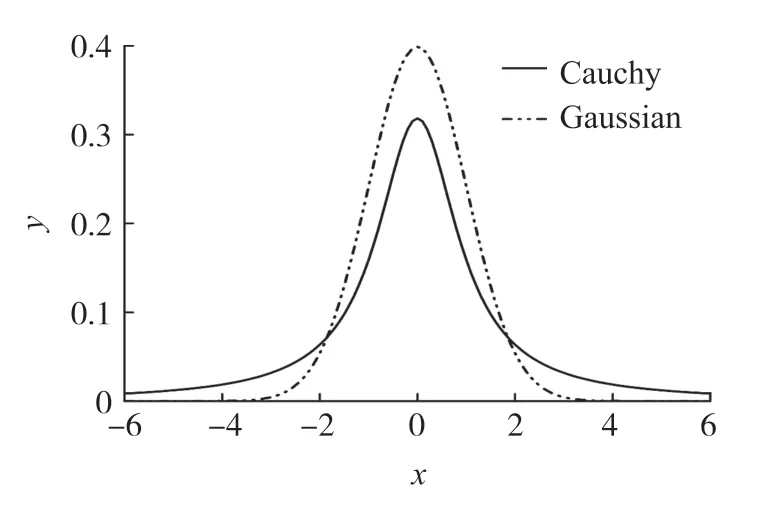
图3 柯西－高斯分布概率密度函数

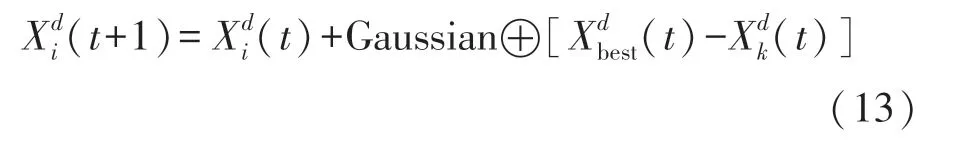
从图3可知，柯西分布两端较长的尾巴可使个体具有更高的概率寻找到全局最优，而高斯分布的中间部分较高，形成的随机数大都集中在较低的数值，所以具有较强的局部开发能力。

判断算法进行前期成虫全局寻优还是后期幼虫局部开发是由蝗虫个体的适应度变化率η决定的，当η连续n代小于某一阈值τ时，则说明算法进入后期的幼虫开发。η公式如下:

式中，fit(x)为蝗虫最优个体的适应度值。

适当的阈值τ很重要，文献[25]表明，当τ＝0.001时，能够有效地判断算法是否进入了后期。

3.2.3 引入最优邻域扰动策略

蝗虫个体在更新位置时，依赖于每次迭代后的位置，未对目标位置主动地做出扰动更新，导致搜寻时间缓慢，因此，引入最优邻域扰动策略，围绕最优位置进行随机搜索，公式如下:

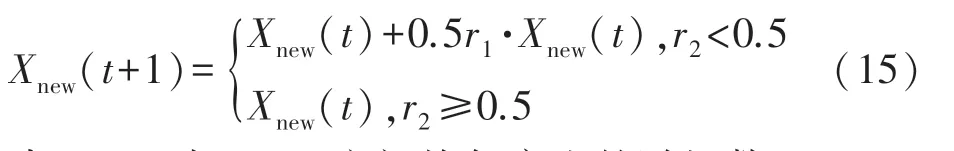
式中，r1、r2为[0，1]之间均匀产生的随机数。

对于主动扰动生成的新位置，不一定是优于原位置，因此采用贪婪机制判断是否保留新位置:

如果主动生成的位置比原位置好，则更新位置，使其成为全局最优。反之，最优位置保持不变。

综上，改进的蝗虫算法流程图如图4所示。

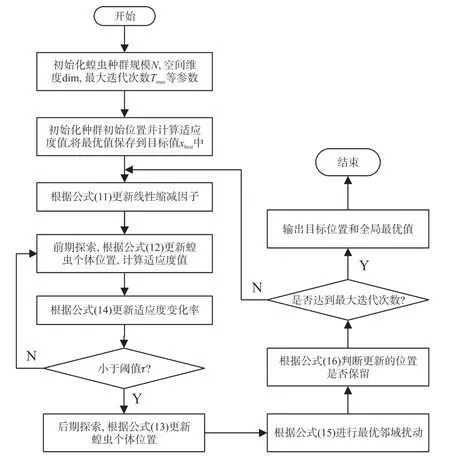
图4 改进的蝗虫优化算法流程图

3.3 算法性能测试

为验证上述改进蝗虫优化算法IGOA的有效性，选取Ackely和Griewangk两个测试函数对其进行性能测试，并与传统GOA和PSO进行比较分析。

Ackely函数在最小值周围也存在很多局部极小值，如图5所示。

图5 测试函数f1

函数表达式如下:

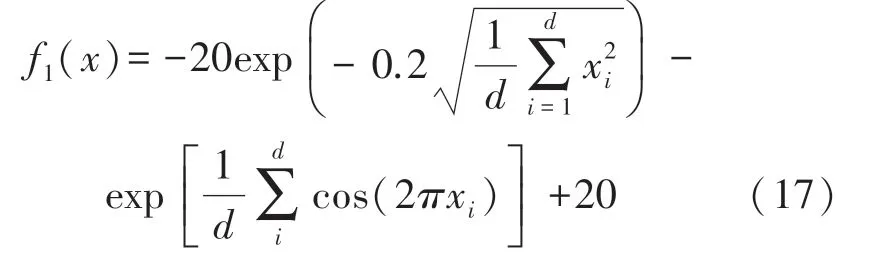
式中，x属于－30到30，定义域内最小值为0。

Griewangk函数的局部极小值呈现有规律的分布，如图6所示，表达式如下:

图6 测试函数f2

式中，x属于－600到600，定义域内最小值为0。

利用MATLAB2020b分别对测试函数进行寻优测试，设置最大迭代次数Tmax＝300，维数d＝3，测试结果如图7、图8。

图7 GOA，IGOA，PSO对函数f1(x)的寻优过程

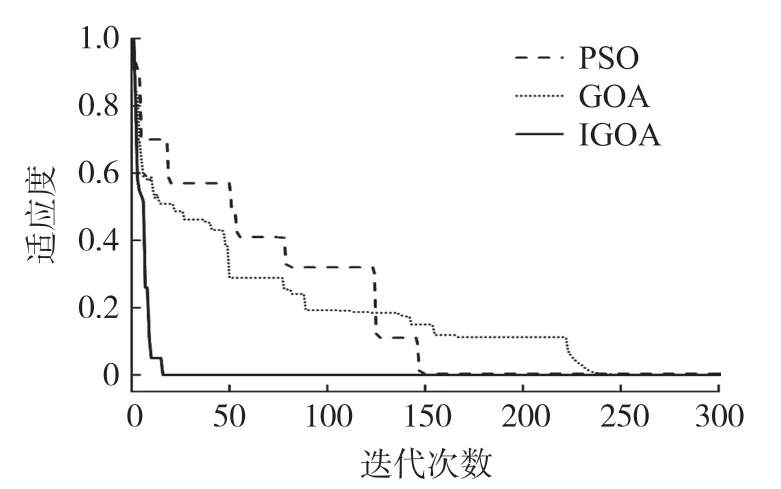
图8 GOA，IGOA，PSO对函数f2(x)的寻优过程

由图7、图8可以看出，在Ackely测试函数中，三种优化算法最终都逐渐收敛。PSO的收敛速度慢于GOA和IGOA，其中，IGOA在迭代19次时就达到最优适应度值。在Griewangk测试函数中，IGOA陷入局部最优的次数比GOA和PSO少很多，且是最快达到收敛，说明IGOA在全局寻优能力和收敛速度上均优于传统GOA。

3.4 IGOA-LSTM的瓦斯浓度预测模型

基于IGOA-LSTM多参数瓦斯浓度预测模型建立过程如图9所示:

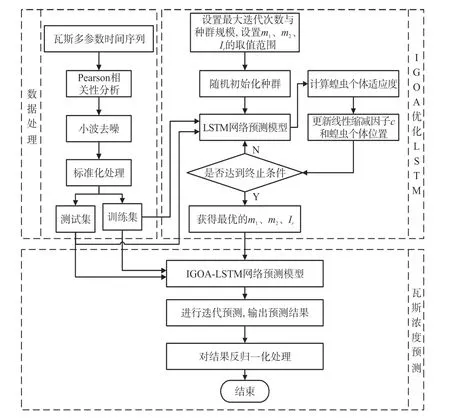
图9 基于IGOA-LSTM网络预测模型

Step 1 将监测到的瓦斯多参数时间序列进行预处理，再对样本数据集按8∶2的比例划分测试集与训练集。

Step 2 设置最大迭代次数Tmax与种群规模N，设置LSTM的三个超参数(第一个隐藏层LSTM单元的个数m1、第二个隐藏层LSTM单元的个数m2，学习率Ir)的取值范围，随机初始化种群。

Step 3 构建LSTM网络模型，将蝗虫位置映射为解，蝗虫个体的适应度值映射为平均绝对百分比误差。

Step 4 根据式(11)更新线性缩减因子c的值，根据式(12)～式(16)更新蝗虫的位置，作为其最优值记录下来。

Step 5 判断蝗虫个体是否达到最大迭代次数，若满足条件，则将最优超参数赋予LSTM，否则返回Step 3。

Step 6 根据IGOA优化之后的最优超参数构建IGOA-LSTM预测模型，输出瓦斯浓度预测值。

3.5 模型评价标准

采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为预测性能评价指标，公式如下:

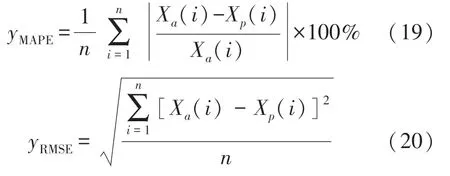
式中，n为预测样本点数，Xa和Xp分别为i时刻的瓦斯浓度真实值和预测值。

4 实例分析

样本数据为某煤矿2019年2月15日至17日，每隔2 min采集一次，共2 000条生产监测数据，包含8个变量:工作面瓦斯浓度/%(X1)、上隅角瓦斯浓度/%(X2)、回风流瓦斯浓度/%(X3)、抽采浓度/%(X4)、累计抽采日流量/m3/min(X5)、工作面风量/m3/min(X6)、温度/℃(X7)、抽采负压/Kpa(X8)。部分数据如表1所示。编程语言为MATLAB2020b，处理器为Intel CORE i5，运行内存12G。

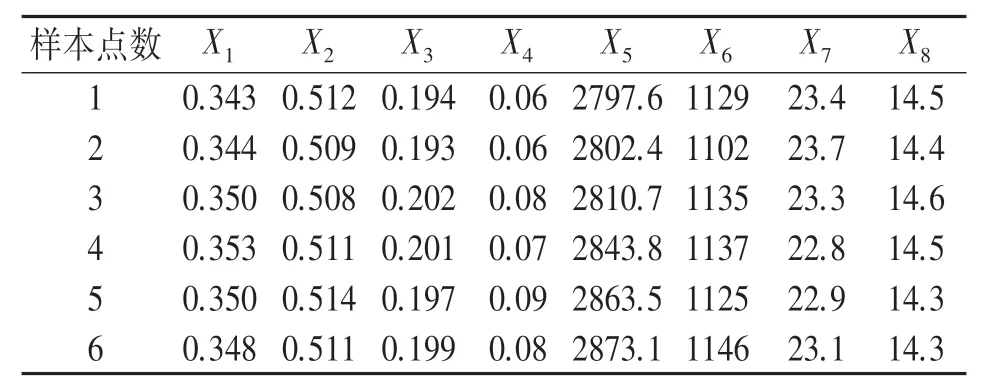
表1 瓦斯浓度及影响因素数据(部分)

4.1 数据预处理

4.1.1 多参数时间序列的相关性分析

对瓦斯多参数时间序列进行Pearson相关性分析，结果如表2所示。

表2 工作面瓦斯浓度与其影响因素的Pearson分析结果

由相关性分析可知，可选取关联度高的上隅角瓦斯浓度、回风巷瓦斯浓度、抽采浓度、温度、工作面风量5个变量作为LSTM的输入特征，实现多参数融合的瓦斯浓度预测。

4.1.2 小波阈值降噪

对多参数时间序列进行去噪处理，以瓦斯浓度为例，选取db4小波进行3层分解，结果如图10所示。从二维时频平面可以看到非平稳时间序列的时频联合特征，频率在0.5×104Hz～3×104Hz的部分，噪声已经被去除了大部分。

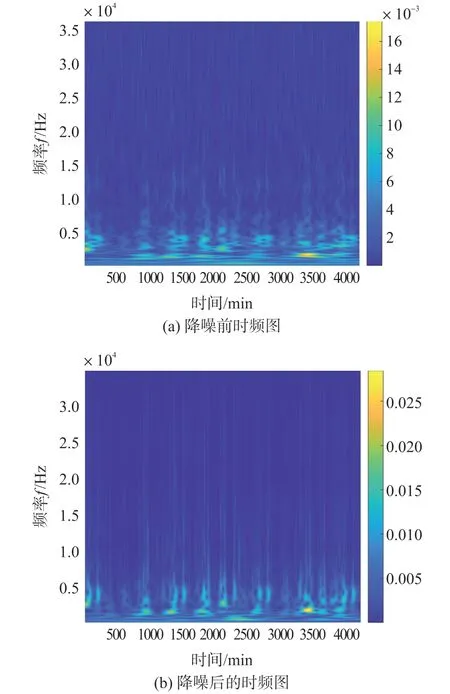
图10 小波降噪前后时频图对比图

4.2 IGOA-LSTM网络模型的训练及超参数的优化结果

GOA-LSTM、IGOA-LSTM两种网络模型的输入层个数为6，隐藏层个数为2，输出层个数为1，种群规模设置为20，最大迭代次数设置为100，m1、m2的搜索范围设置为[0，100]，Ir的搜索范围设置为[0.001，0.01]；同时利用训练集样本构建LSTM网络模型，经多次实验，设置LSTM的m1＝25，m2＝10，Ir＝0.001。寻优过程中GOA算法与IGOA算法的蝗虫个体适应度变化过程如图11所示。

图11 适应度变化曲线对比图

由图11可知，IGOA找到最优解的过程优于GOA，且适应度值更小，说明IGOA比GOA具有更强的跳出局部最优的能力和更快的收敛速度，即具有更高的寻优性能。

GOA算法最终寻找到的最优LSTM的模型参数为m1＝45，m2＝75，Ir＝2.206×10－3。IGOA算法最终寻找到的最优LSTM的模型参数为m1＝10，m2＝10，Ir＝1.813×10－3。

4.3 预测结果分析

4.3.1 小波降噪前后预测结果对比分析

为分析小波降噪对瓦斯浓度预测精度的影响，将降噪前后的2000组数据按8∶2划分训练集与测试集，分别用LSTM预测进行对比实验，结果如图12和表3所示。

表3 降噪前后预测误差

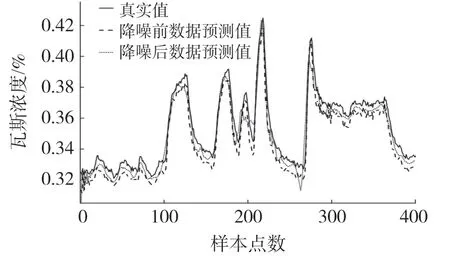
图12 数据降噪前后预测结果

由图12和表3可以看出降噪后的预测值更贴近真实值，RMSE和MAPE指标的值分别下降了26.64%、34.90%。由于瓦斯浓度数据存在噪声，直接预测会导致拟合效果较差，而小波去噪可以滤除高频部分，从而使预测精度有所提升。

4.3.2 单一瓦斯预测与多参数瓦斯预测结果对比分析

为体现多参数融合瓦斯浓度预测的优势，采用LSTM模型进行单一瓦斯浓度预测与多参数瓦斯浓度预测的对比实验，设置迭代次数为50，结果如表4所示。由于多参数融合的瓦斯浓度预测结合了上隅角瓦斯浓度、抽采浓度等五个因素，测试过程所消耗的时间比单一因素瓦斯预测要多；同时观察预测误差值可知，多参数融合的瓦斯浓度预测精度更高，验证了多参数瓦斯浓度预测方法的有效性。

表4 单一瓦斯预测与多参数瓦斯预测结果

4.3.3 不同预测模型对比分析

为验证本文所提模型能够有效提高多参数瓦斯浓度的预测精度，将IGOA-LSTM模型与下列几种模型进行对比:BP、LSTM、PSO-LSTM、GOA-LSTM。其中，BP网络的最大迭代次数设置为100，学习率设置为0.0001，动量因子设置为0.1；PSO-LSTM模型中，最大迭代次数设置为100，种群数量设置为20，动量因子c1、c2均设置为1.49。实验结果如图13和表5所示。

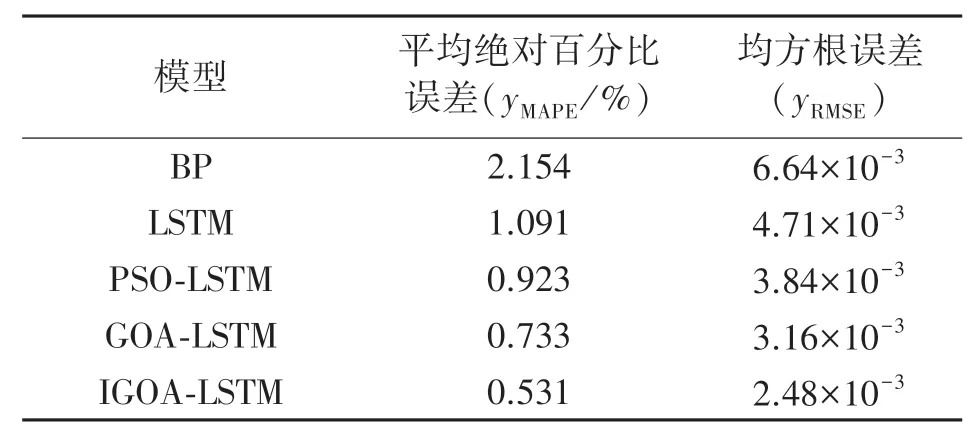
表5 不同模型预测误差对比

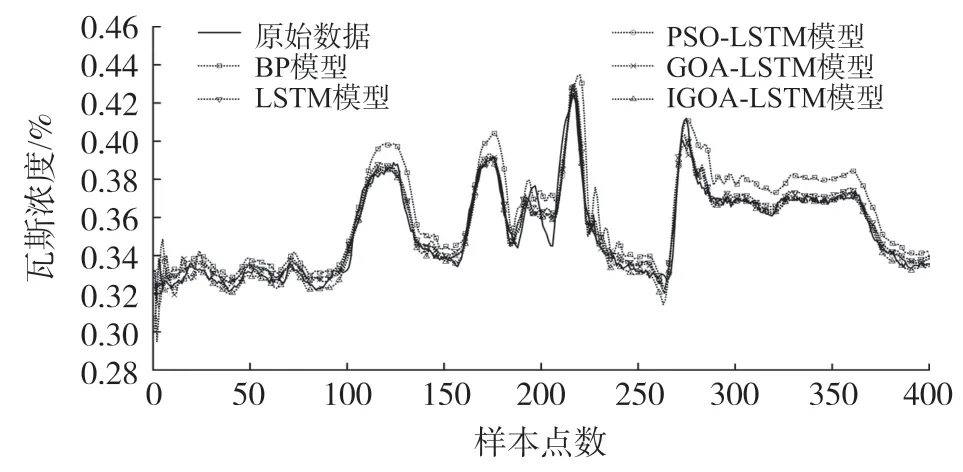
图13 瓦斯浓度预测曲线与实际曲线对比图

从结果分析可知，IGOA-LSTM模型预测误差均低于其他4种模型，瓦斯浓度的预测误差MAPE仅为0.531%。其中BP模型结构相对简单，在面对长时间序列时表现不佳，预测误差最大，MAPE指标比本文模型高出3倍；PSO-LSTM模型和GOA-LSTM模型因为有PSO和GOA算法的参数寻优，使得MAPE指标分别比LSTM降低了15.86%、33.18%。IGOA-LSTM模型MAPE指标和RESE指标的值分别为0.531%和2.48×10－3，均低于其他对比模型，说明预测精度最高，验证了将IGOA-LSTM模型用于提高瓦斯浓度预测精度的有效性。