风致驰振型压电－电磁复合俘能器等效电路建模及参数影响分析*

王红艳，胡嘉睿，隽文烁，韩 刚，刘 尚

(齐齐哈尔大学机电工程学院，黑龙江 齐齐哈尔 161006)

随着无线传感器技术的快速发展和低功率电子产品的大量涌现，可再生能源研究得到了人们广泛的关注。太阳能、风能、波浪能、热能、机械振动能等都可以被收集并转换为电能加以利用。一些研究人员将关注点放到风致振动能量俘获上。风致振动有颤振[1]、驰振[2]、涡激振动[3]等多种形态。驰振一般发生在正方形、矩形、直角形等复杂不规则的非流线型截面的结构中。驰振产生的机理是由于升力曲线具有负斜率，使得空气升力具有负阻尼作用，结构能够源源不断地从外界吸收能量，从而形成自激振动现象。

在小风能俘获研究中，振子通常采用压电或电磁元件进行换能。基于准静态假设[4]，很多研究人员已经建立了风致驰振型压电或电磁俘能器的数学模型，研究了钝体截面形状[5－9]、外接负载[10－12]、机电耦合系数[13]、机械参数[14]、非线性力[15]等对俘能器切入风速和系统输出性能的影响关系。这些研究多是直接连接线性负载进行分析。也有一些研究人员从实际应用角度出发，通过建立风致驰振型压电俘能器的等效电路模型，以此实现与非线性接口电路相连的压电俘能器发电性能的评估[16－17]。

为了提高系统发电能力，一些研究人员对压电－电磁复合俘能器进行了研究。对于压电－电磁复合俘能器，由于压电元件和电磁元件内阻抗相差较大(压电元件内阻抗可达到几十或几百千欧，电磁元件内阻抗只有几十或几百欧)，压电－电磁复合俘能器通常采用双端口输出的形式直接为不同数量级的负载电阻供能[18－19]。一些研究已经表明，双端口分别连接线性负载后，总体输出功率有所提升，但每个端口输出功率均低于单一机电换能器使用时的输出功率[20－21]。上述研究通常考虑最优电阻配置，但实际应用时，外接负载阻抗通常很难达到压电元件的内阻抗值，通常需要考虑利用压电元件为低阻抗负载供能。压电元件在连接低阻抗负载时具有低功率的特性，这为利用电磁元件进行补充发电提供了可能。如何有效利用压电－电磁复合俘能器提高系统输出功率目前仍然是研究人员关注的焦点。

考虑到压电电磁复合俘能器双端口分开供能会引起端口的输出功率的下降，本文将两个标准直流接口电路的输出端口进行串联和并联连接，通过等效电路法对与标准直流接口电路相连的风致驰振型压电－电磁复合俘能器进行功率评估，仿真分析压电－电磁复合俘能器在为单一负载供能时的发电性能。本文研究内容安排如下:首先建立风致驰振型压电－电磁复合俘能器的数学模型，然后根据机械量和电学量的类比关系进行等效电路建模，并在SIMetrix软件中进行模型的电学表达。随后将电路仿真结果与数值分析结果比较验证等效电路模型的正确性。最后与标准直流接口电路相连，仿真分析激励风速和负载电阻对俘能器输出功率的影响关系，并与单一压电和单一电磁俘能器输出功率进行比较，分析压电－电磁复合俘能器的发电性能。

1 风致驰振型压电－电磁复合俘能器数学模型和等效电路模型

图1(a)和1(b)所示分别为风致驰振型压电－电磁复合俘能器结构简图和集中参数模型。图1(a)中，俘能器由压电悬臂梁(金属梁上粘贴压电片)、方形截面钝体、磁铁和线圈组成。悬臂梁一端连接基座，另外一端连接钝体和永磁铁。当激励风速U超过钝体结构俘能器的切入风速时，钝体横风向驰振，悬臂梁产生形变，压电片输出电压。磁铁与固定线圈存在相对运动，线圈内部产生感生电流。图1(b)中，M、K和D分别代表压电－电磁复合俘能器等效质量、等效弹簧刚度和机械阻尼。Fz为气动力。u为质量M的运动位移。Cp为压电片静态夹持电容。θp为压电元件的机电耦合系数。Vp为压电接口电路两端电压，Ip为流过压电接口电路的电流。Lc和Rc分别为线圈电感和内阻。θe为电磁元件的机电耦合系数。Ie为流过线圈及接口电路的电流，Ve为电磁接口电路两端电压。

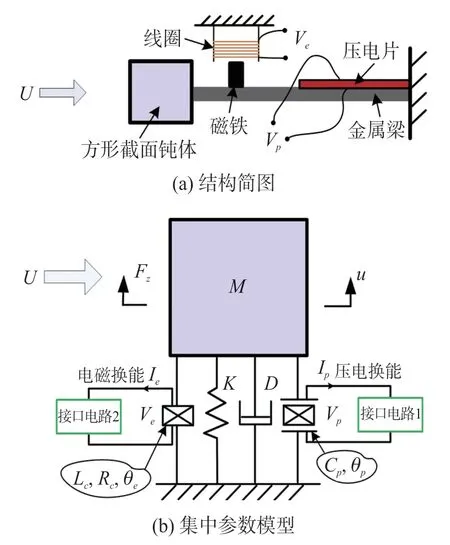
图1 风致驰振型压电－电磁复合俘能器

风致驰振型压电－电磁复合俘能器本构方程为

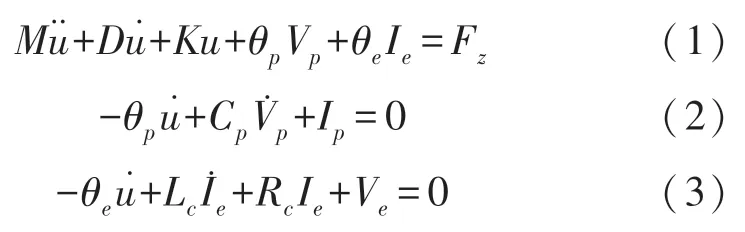
式中，和分别为质量M的运动速度和运动加速度。式(1)中，方形截面钝体结构气动力为:

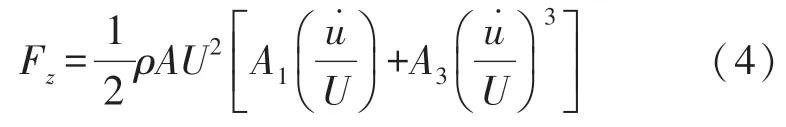
式中，ρ为空气密度，A为钝体迎风面面积，A1和A3为气动力经验系数。

表1所示为俘能器机械和电气参数的类比关系。根据机电参数类比关系，风致驰振型压电－电磁复合俘能器本构方程(1)～(4)可以写成等效电路方程(5)～(7)的形式。

表1 机械参数和电学参数类比关系

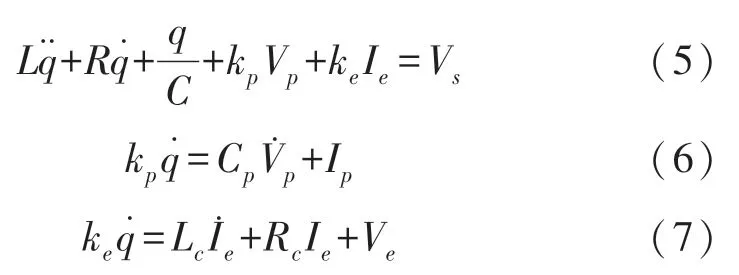
式中，电荷q＝CVc，Vc为电容C两端电压。根据式(4)，电压源电压Vs可以表达为:

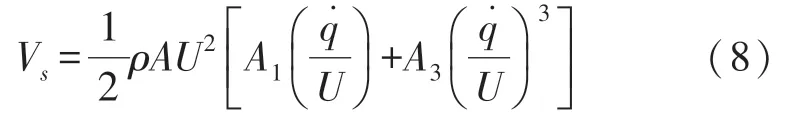
利用SIMetrix软件，可以建立风致驰振型压电－电磁复合俘能器的等效电路图，如图2所示。图2中，任意电压源(Arbitrary Source)代表气动力。电流I(iin)＝。压电耦合由一个电压控制电压源和一个电流控制电流源模拟。电磁耦合由两个电流控制电压源模拟[22]。

对于单一压电俘能器电路仿真，可将图2中的电磁耦合及后续电路部分去掉，系统等效电路方程为:

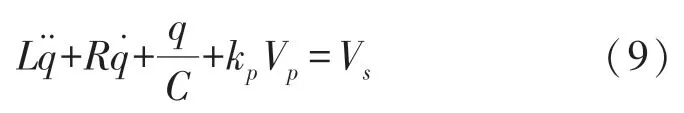
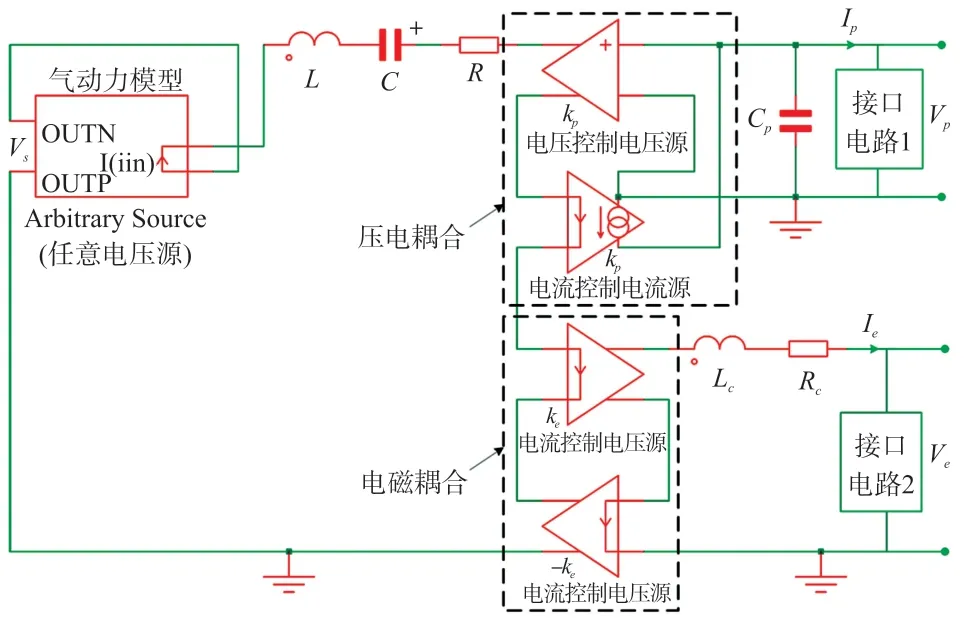
图2 风致驰振型压电－电磁复合俘能器等效电路图

对于单一电磁俘能器电路仿真，可将图2中的压电耦合及后续电路部分去掉，系统等效电路方程为:

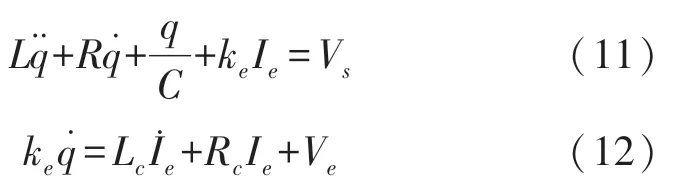
2 等效电路模型仿真的数值验证

为了验证等效电路模型计算的正确性，压电和电磁元件接口电路用纯负载电阻R1和R2代替，此时方程(2)和(3)可写为:

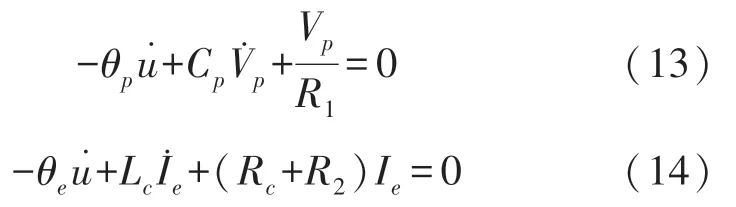
使用MATLAB软件自带的ODE45函数(龙格－库塔方法)进行微分方程数值求解，定义状态空间矢量:

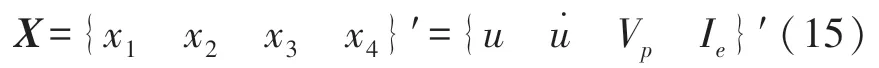
根据定义的状态空间矢量，对式(1)、式(13)和式(14)进行变换，整理得到压电－电磁复合俘能器的状态空间表达式为:

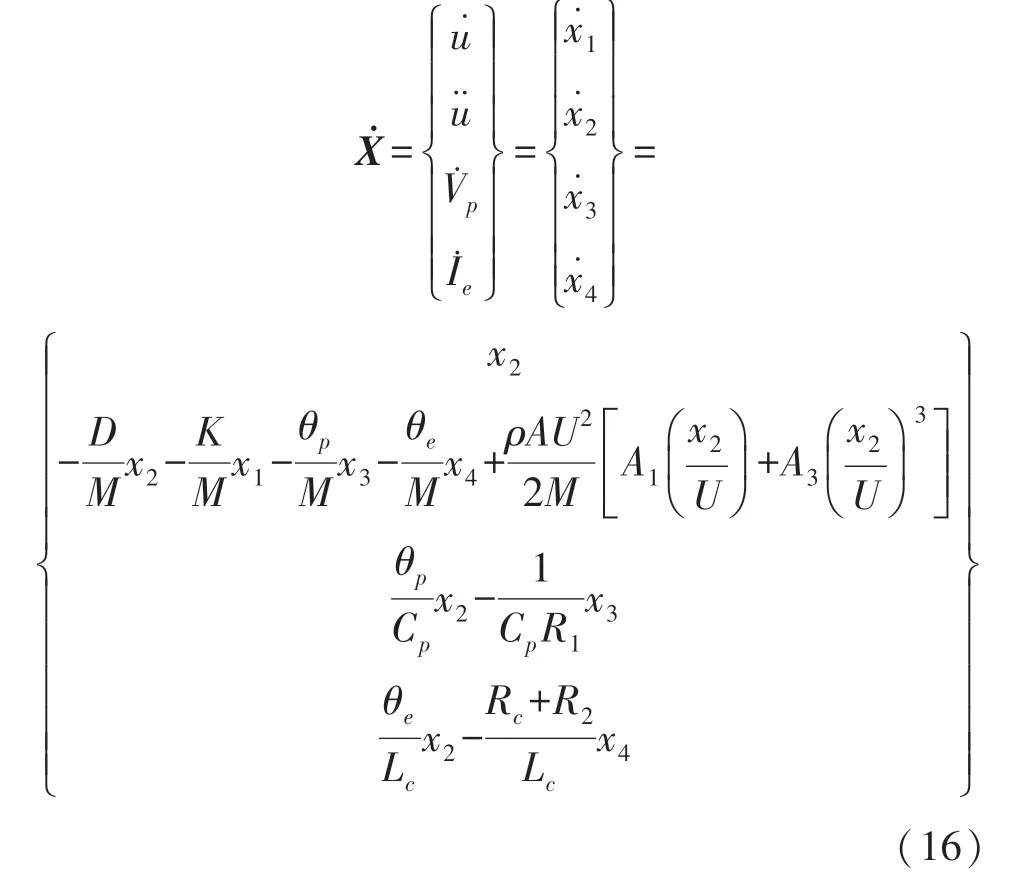
根据文献[17]和[23]中的模型参数设置本文使用仿真参数为:M＝0.002 738 kg，D＝0.006 5 Ns/m，K＝31.5 N/m，A＝0.002 m2，ρ＝1.204 1 kg/m3，A1＝2.3，A3＝－18，Cp＝25.7 nF，Rc＝16.8Ω，Lc＝0.006 8 H，θp＝0.000 09 N/V，θe＝1.33 N/A。根据表1，等效电路参数L＝27.38 mH，R＝6.5Ω，C＝1/K＝31.7 mF，kp＝0.000 09，ke＝1.33。数值分析时设置周期数为300个，每个周期上取50个点。压电元件输出平均功率的计算公式为:

式中，Vpmax为俘能器驰振时，仿真分析得到压电元件在最后一个周期的最大输出电压。

电磁输出平均功率的计算公式为:

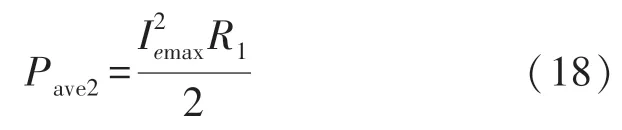
式中，Iemax为俘能器驰振时，仿真分析得到电磁元件在最后一个周期的最大输出电流。

为了模拟初始扰动，等效电路仿真时，电容C上施加了一个5μF的初始电压。通过测量电容C两端的电压，利用公式q＝CVc可以计算俘能器的振动位移。设置R1＝200 kΩ，R2＝2 kΩ。图3所示为带交流接口的压电－电磁复合俘能系统最大输出位移以及压电和电磁元件的平均输出功率与激励风速的关系图。从图3(a)和图3(b)中可以看出，切入风速约为3.2 m/s，达到并超过切入风速后，进一步增加风速，系统最大位移、压电及电磁元件的平均功率均增加。等效电路模型仿真结果和数值计算结果非常接近，说明建立的等效电路模型及其在SIMetrix软件中的模型表达都是正确的。等效电路模型的正确建立为后续连接标准直流接口电路进行电学仿真分析打下了基础。

图3 带交流接口的压电－电磁复合俘能系统最大位移、压电和电磁平均输出功率与激励风速关系图

3 带标准直流接口电路的参数影响分析

3.1 整流输出端口并联连接

图4(a)和4(b)所示分别为与直流接口电路相连的压电－电磁复合俘能器的机械－电路原理图及其等效仿真电路(整流桥输出端并联连接)。图4(a)和4(b)中，每个标准直流接口电路由四个二极管连接起到整流作用。Cf为滤波电路。

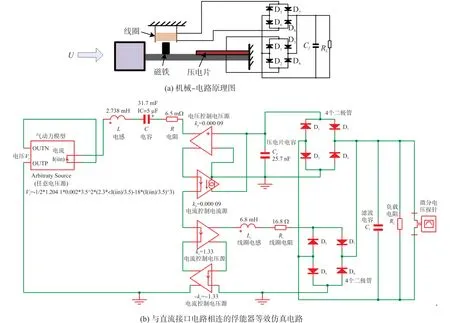
图4 与直流接口电路相连的压电－电磁复合俘能器及等效仿真电路(整流桥输出端口并联)

图5所示为不同风速条件下(U＝3.5 m/s，4 m/s，5 m/s)，压电－电磁复合俘能器，单一压电俘能器、单一电磁俘能器输出功率随负载参数RL的变化关系图。从图5(a)、5(b)和5(c)中可以看出，风速越高，俘能器输出功率越大。在低负载电阻区域(RL≤Rcritical)，压电－电磁复合俘能比单一压电和单一电磁俘能具有更高的输出功率；随着激励风速的增加，压电－电磁复合俘能器在较低的负载电阻区域获得最优功率输出(见图5(b)和5(c))，其变化趋势与单一电磁俘能器的功率－负载变化趋势一致。这说明电磁元件功率输出受风速影响比压电元件大。电磁元件功率随风速增加的速度明显要快于压电元件。当电磁功率逐渐占据主导地位时，俘能器在较小的负载电阻处出现功率峰值。从图5(a)、5(b)和5(c)中还可以看出，在高负载电阻区域(RL＞Rcritical)，压电－电磁复合俘能的输出功率与单一压电俘能输出功率基本相同，而单一电磁俘能随着负载电阻值的增加，输出功率急剧下降。以上分析表明，带直流接口的压电－电磁复合俘能器只适合工作在低阻抗负载区工作。合理使用可以提高系统的输出功率。

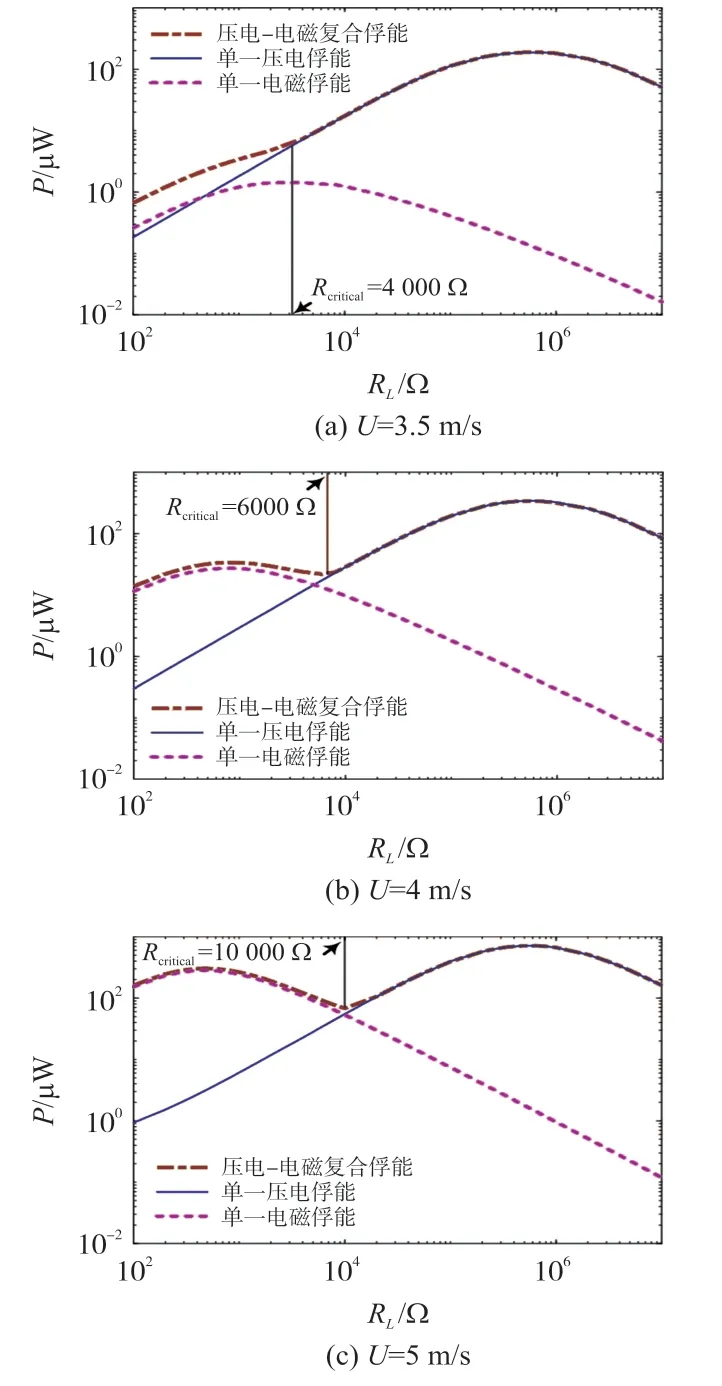
图5 风速和负载电阻对俘能器输出功率的影响(压电－电磁复合俘能时整流桥输出端并联)

3.2 整流输出端口串联连接

图6(a)和6(b)所示分别为与直流接口电路相连的压电－电磁复合俘能器的机械－电路原理图及其等效仿真电路(整流桥输出端串联连接)。图7所示为不同风速条件下的负载参数RL对俘能器功率的影响关系图。从图7(a)、7(b)和7(c)中可以看出，压电－电磁复合俘能器输出功率明显小于单一压电或单一电磁俘能器，说明俘能系统直流接口输出端串联连接引起的相位差会明显降低系统输出功率，降低系统发电性能。

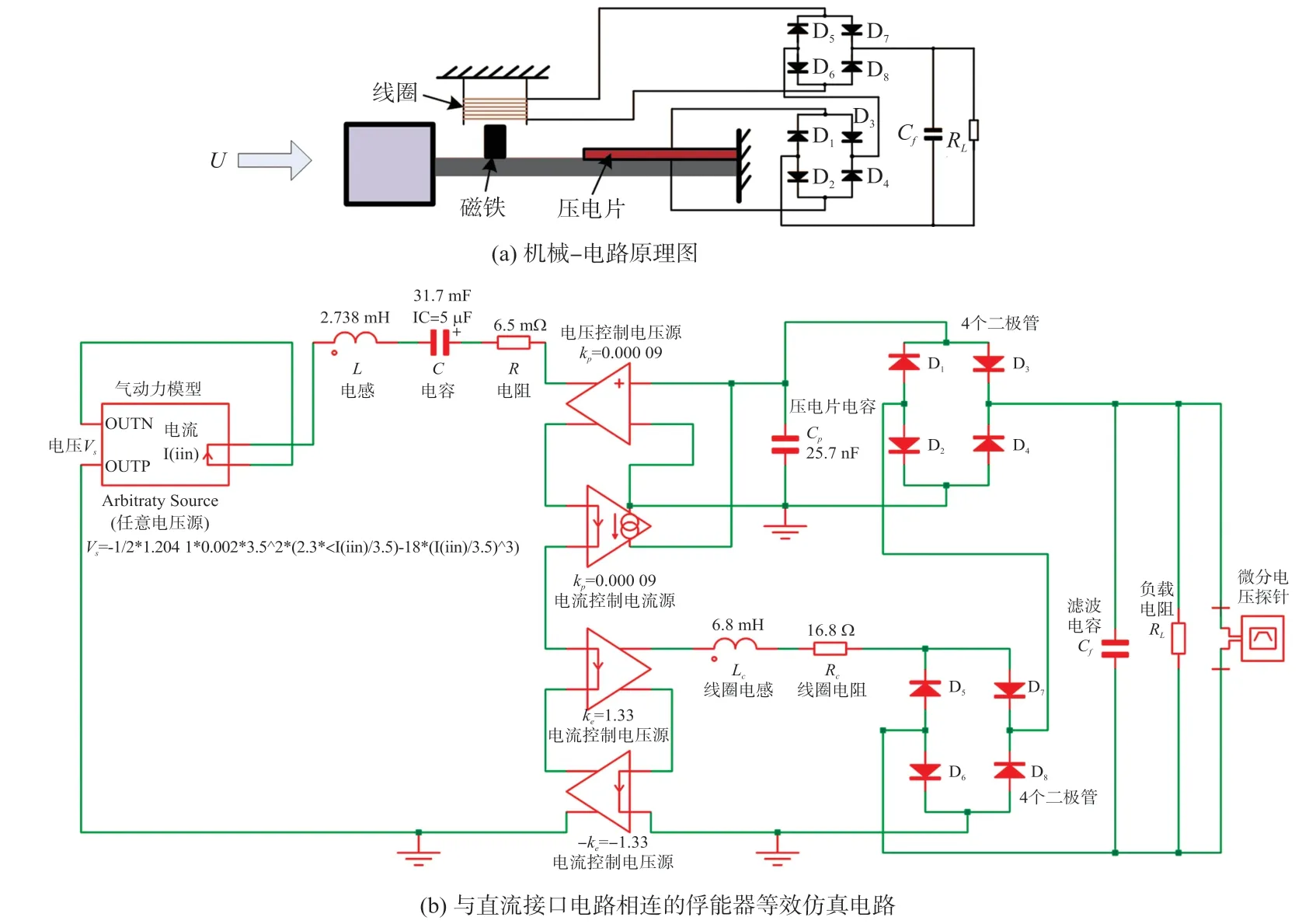
图6 与直流接口电路相连的压电－电磁复合俘能器及等效仿真电路(整流桥输出端口串联)

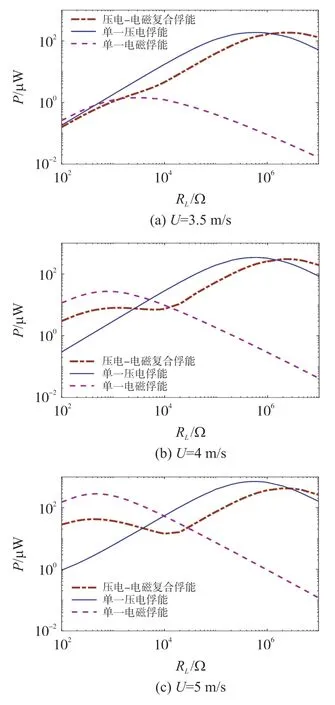
图7 风速和负载电阻对俘能器输出功率的影响(复合俘能时整流桥输出端串联)

4 结论

本文建立了风致驰振型压电－电磁复合俘能器的等效电路模型，并在SIMetrix软件中进行了等效电路的电学表达。通过与龙格库塔法数值求解结果比较验证了等效电路模型建立的正确性。在此基础上，将等效电路模型与标准直流接口电路相连，仿真分析了激励风速和负载电阻对俘能器输出功率的影响关系。本文分别分析了整流桥输出端口并联和串联连接的压电－电磁复合俘能器的功率性能。得到的分析结论如下:

①与直流接口电路输出端串联连接方式相比，直流接口电路输出端并联连接可提供更高的输出功率。

②直流接口电路输出端并联连接低阻抗负载后，随着风速的增加，电磁输出功率逐渐占据主导地位，俘能器出现功率峰值。相比于单一压电和单一电磁俘能器，复合俘能器获得了更高的输出功率，显示出复合俘能在为低负载阻抗供能时的优势性能。

③直流接口电路输出端并联连接高阻抗负载后，压电－电磁复合俘能器与单一压电俘能器的输出功率相当，表明了电磁俘能在为高阻抗负载供能时的不适用性。