二维多关节机器鱼远场流速和攻角预测研究*

刘科显，孟庆浩，徐雪寒

(天津大学电气自动化与信息工程学院，天津市过程检测与控制重点实验室，机器人与自主系统研究所，天津 300072)

流场环境感知是水下机器人基本功能，而人造侧线系统是目前这一领域研究的热点之一。侧线是一种鱼类独有的器官，可以感知流场压力、流速、温度和盐度等流场信息[1]，也可以用来辨别附近是否存在障碍物。

受侧线的结构和功能启发，研究人员已提出多种人造侧线系统。Sharif等[2]利用离子聚合物与金属复合材料研制一种可以覆盖在机体表面的微型压力传感器；Abels等[3]设计了一种基于压力应变片的机体表面微型流速传感器，可较为精确地感知流速；李渊等[4]设计了能有效感知水流信息的“人工侧线”系统，李振等[5－6]设计一种以鱼类侧线为基础的MEMS水听器，并采用有限元技术对封装结构进行优化设计。

在应用方面，吴乃龙等[7]详细分析了鱼类侧线功能，并实现了水流场识别；Zheng等[8]利用压力传感器捕捉流场中的涡街信息，实现了对相邻仿鱼机器人的位置和运动状态的感知；Xu等[9]采用最优权重分析算法优化了“人工侧线”系统的传感器排布方式；Carryon等[10]将感知反馈策略应用于波动推进驱动器，提高了仿鱼机器人的运动性能。刘贵杰团队[11－13]建立了基于压力传感器的静态“人工侧线”系统，采用机器学习技术实现流场流速、物体位置等信息的流场结构反演。林兴华[14]等采用CFD方法获得不同类型障碍物的流场特征，采用支持向量机预测不同类型的流场目标。Salumäe等[15]采用人造侧线系统辨识机体运动速度等运动状态信息。Tallapragada等[16]分析了水翼摆动推进工况下翼型周围流场分布状态，可进一步用于分析仿生机器鱼周围流场规律。目前，对于鱼类推进机理的研究主要以鳗鲡和鲹科鱼类为主，但一般在单刚体或者柔性结构上安装人造侧线系统。

为扩展人造侧线系统的应用范围，本文以仿鲹科鱼类游动的二维多关节机器鱼为研究对象，将压力传感器阵列人造侧线系统应用到具有多关节特征的机器鱼结构上，研究在广阔水域中多关节机器鱼对远场流速和攻角的感知方法。以Joukowski翼型作为二维机器鱼包络外形，在机器鱼的头部和鱼体两侧设置11个压力监测点，通过组合各压力监测点输出值给出了四种测量模型。应用势流理论和伯努利方程分析Joukowski翼型表面压力和流速，并结合Fluent软件分析远场流速和攻角与四种测量模型输出值之间的关系，采用最小二乘多项式回归方法建立四种测量模型的回归方程。最后采用SIR粒子滤波实现以四种测量模型输出值对远场流速和攻角的预测。

1 摆动状态Joukowski对称翼型体表压力分析

设翼型处于无限大的流场中，远场流速为V∞，翼型攻角为α。定义流场参数为Λ＝(V∞，α)。通过式(1)所示的保角映射，转化到复平面内的圆盘分析，即

式中，z表示翼型上某点，ξ为z在复平面上的映射，b0表示复平面圆盘圆心位置，此处可定义成b0＝R－｜ξ0｜，R表示转换后圆盘直径，ξ0表示圆盘圆心的位置，故Joukowski对称翼型在复平面内可以用R和ξ0表示。则翼型周围流场复势可以表示为[16]:

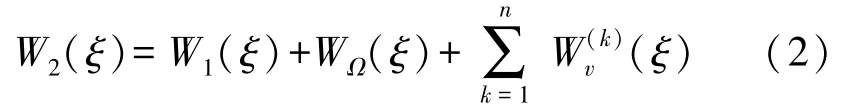
式中，W1(ξ)为翼型固定时周围流场的复势，定义Γ为速度环量，根据势流理论和Kutta条件可以写出:

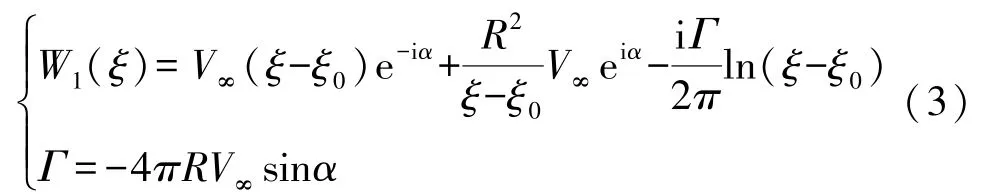
式(2)中:设Ω为翼型摆动的频率角速度，WΩ(ξ)表示与翼型摆动相关的复势，该项可表示为[16]:

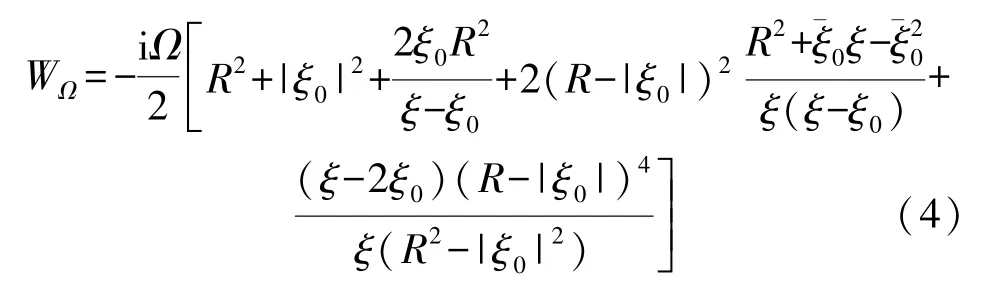
式(2)中:W(k)v(ξ)为第k个涡的速度势，根据Milne-Thomson圆定理，该项可表示为[16]:

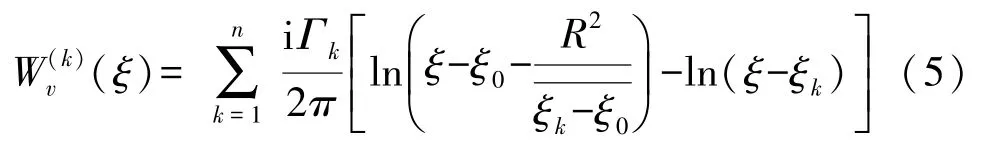
式中，Γk为第k个涡的速度环量，ξk表示第k个涡的位置。翼型表面共轭速度场是速度势的位置梯度，设翼型上某点流速为v(z)＝u＋iv，则共轭流速¯v2(z)在复平面内可表示为:

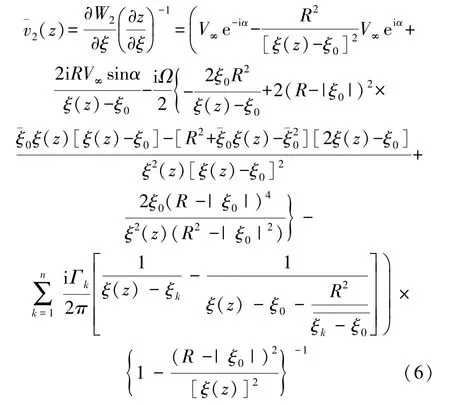
式中，ξ(z)为复平面内一点到z平面的逆映射，可表示为

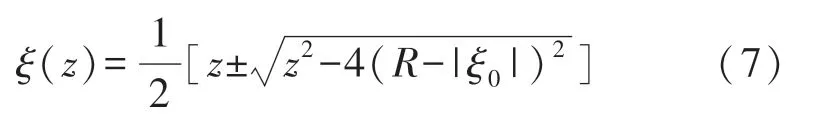
假设翼型摆动的角速度为Ω＝2πf，代入式(6)中并简化可得

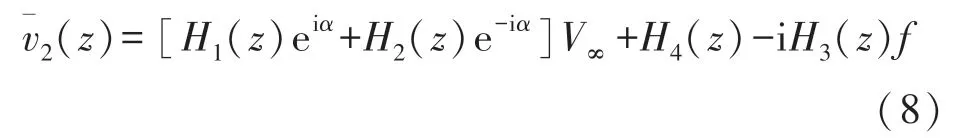
式中，H1(z)、H2(z)和H3(z)为关于翼型上某点位置z的函数，H4(z)是表征涡位置的参数。将上式中的指数项泰勒展开并取前两阶，则式(8)所述的¯v2(z)可表示为

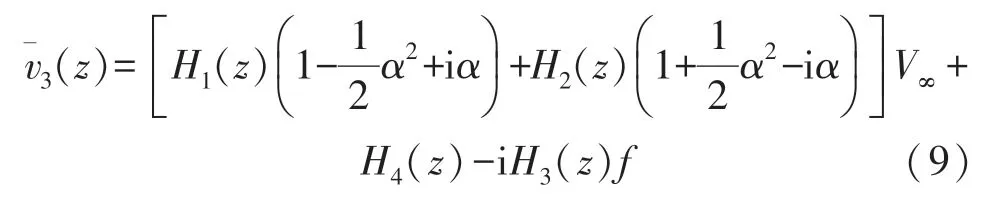
式中，¯v3(z)的模为位置z处的流速，将式(9)代入伯努利方程，则翼型上任意一点的静压可表示为

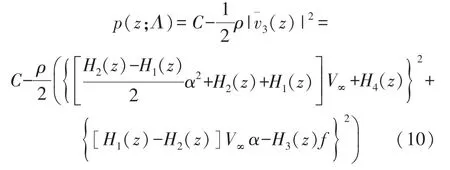
式中，p(z；Λ)为流场参数Λ下翼型上位置z处的体表压力；C为流场常量；ρ为流体密度。

为了消除流场常量C的影响，设翼型上任意指定两点z1和z2的压力差为:

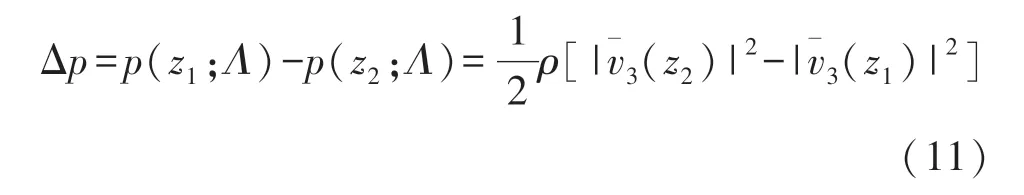
从式(10)中可以得出，翼型上任一点压力可以分成两部分，一部分是由流场参数Λ决定，第二部分是由流场参数Λ和摆动频率f耦合作用。

多关节机器鱼周围流场较为复杂，难以根据势流理论建立体表压力模型，需采用商业CFD软件Fluent分析多关节机器鱼体表压力与远场流速V∞和攻角α特性。

2 二维多关节机器鱼仿真模型及鱼体波动方程

2.1 二维多关节机器鱼几何模型

本文所采用的二维多关节机器鱼模型如图1(a)所示，其中B0为鱼头，B1、B2和B3为鱼身，B4为机器鱼尾鳍。鱼头和鱼身为Joukowski对称翼型，尾鳍为NACA0013翼型，鱼体总长为320 mm，其中鱼身长度168 mm，在鱼体周边均匀分布11个压力监测点。迎着鱼头观察，左侧压力监测点分别命名为s11、s21、…、s51，右侧压力监测点分别命名为s12、s22、…、s52，在鱼头正中处设置压力监测点s0。

采用如图1(b)所示组合网格方案，机器鱼周围流场采用三角形网格，远处流场采用四边形网格。

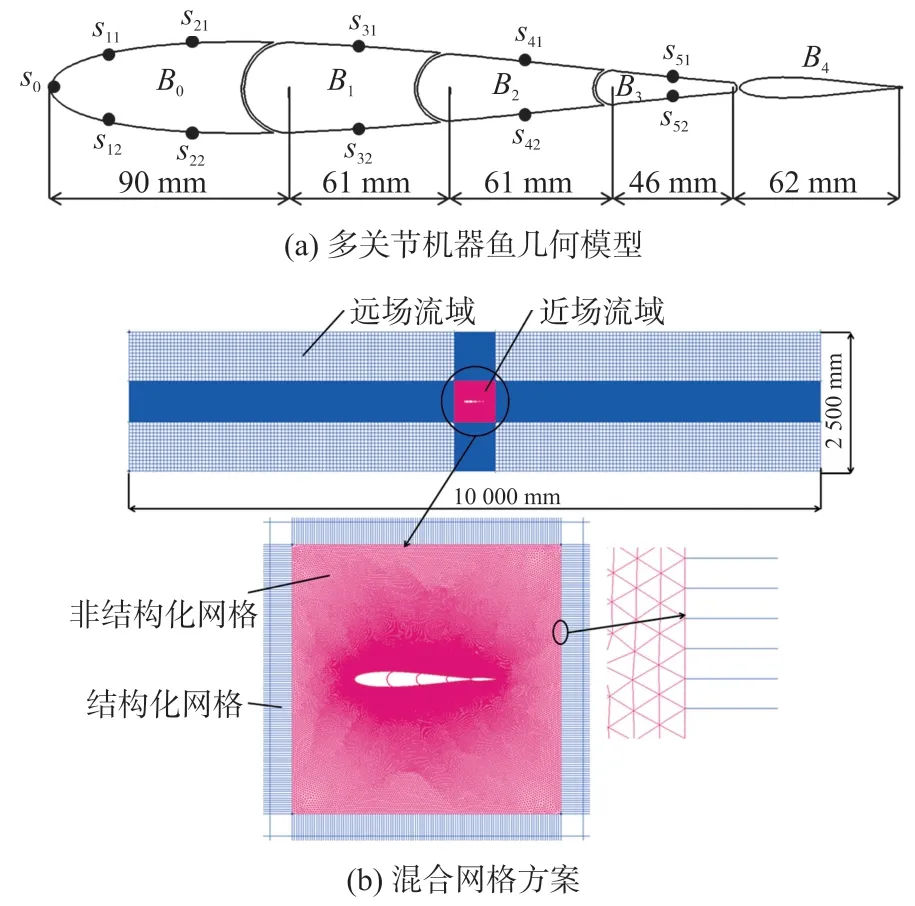
图1 多关节机器鱼模型

2.2 鱼身波动方程

鱼身部分波动规律需符合Lighthill[17]提出的鲹科鱼类鱼体波方程拟合，如式(12)所示。

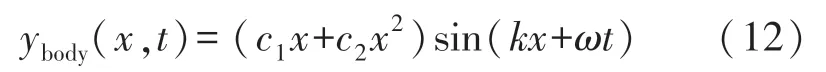
式中，ybody为鱼体的横向位移，x为鱼体的纵向位移，c1和c2为波幅包络线系数，k＝2π/λ为鱼体波波数，ω＝2πf为鱼体波角频率。其中λ表示鱼体波波长，f为鱼体波摆动频率。

将鱼体波方程在一个周期内离散，可得到如式(13)所示的一组离散后的鱼体波曲线簇。

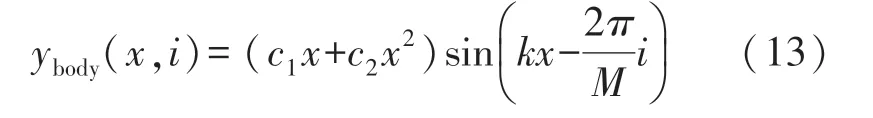
式中，M为鱼体波在一个周期内的离散数量，本文取M＝18，i为曲线簇中的曲线编号，取值范围为0～M－1，定义c1＝0.12，c2＝0.21，波长λ取1.5倍体长，假设构成鱼身的各段旋转中心位于鱼体波曲线上，则可得式(14)表示的各连杆转动规律，

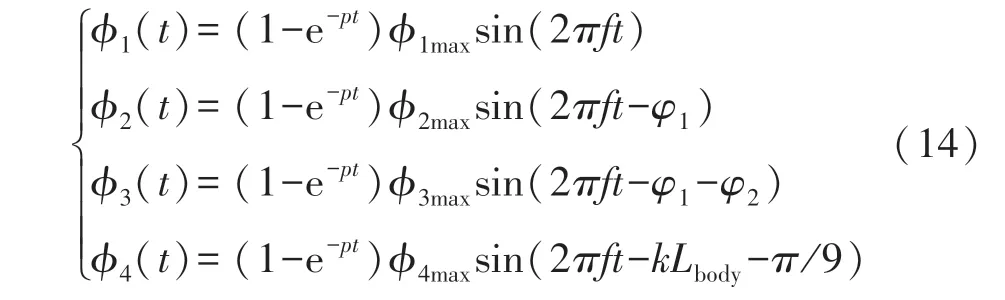
式中，φ1max、φ2max、φ3max和φ4max分别为鱼身B1、B2和B3段以及尾鳍B4最大转角；φ1为B2相对于B1滞后的相位差；φ2为B3相对于B2的相位差；f为摆动频率；t为摆动时间；p为指数系数；Lbody为鱼身长度。

3 多关节机器鱼体表压力分析

3.1 压力系数测量模型

各压力监测点数值随着鱼体波动呈周期性变化，需对采样数据做式(15)所示的时间均值处理以及无量纲化处理。

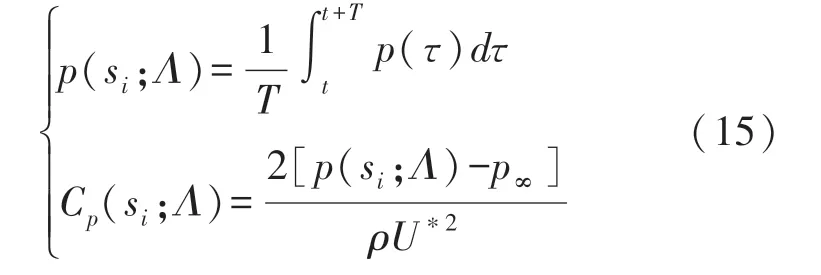
式中，p(si；Λ)为经过时间均值处理后的压力值，Cp(si；Λ)为监测点si在流场参数为Λ条件下测量的无量纲压力系数；p∞为远场压力或参考压力，此处选一个大气压；U*为参考速度，数值上等于鱼体波波长λ。建立以下四种测量模型，分别命名(1)单点传感器，标记s；(2)交叉传感器，标记为sopp；(3)相邻传感器，标记为sadj，(4)对称传感器，标记为ssym。按照式(15)所给出的无量纲压力系数Cp(si；Λ)的定义，四种测量模型各测点输出值可以写成式(16)的形式。

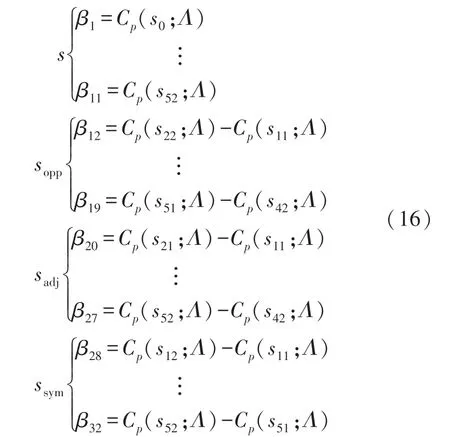
式中，s、sopp、sadj和ssym分别表示单点传感器、交叉传感器、相邻传感器和对称传感器模型；βi(i＝1，…，32)为四种测量模型测点输出值。

3.2 静水环境下机器鱼体表压力特征

设二维机器鱼处于静水环境，鱼体按照式(14)摆动，设摆动频率为1 Hz，机器鱼一个摆动周期内压力场云图以及体表压力时空分布情况分别如图2和图3所示。

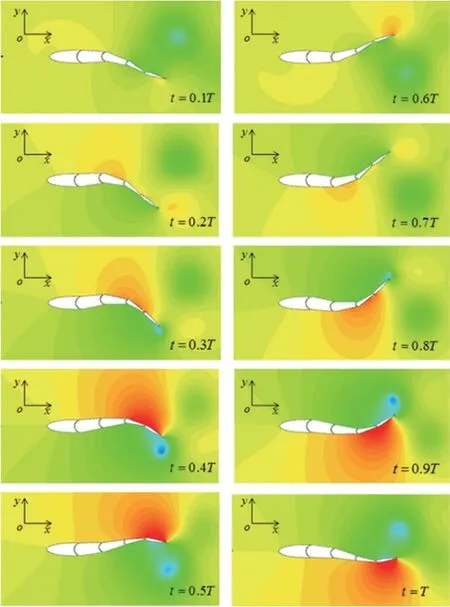
图2 单个摆动周期内的压力场云图

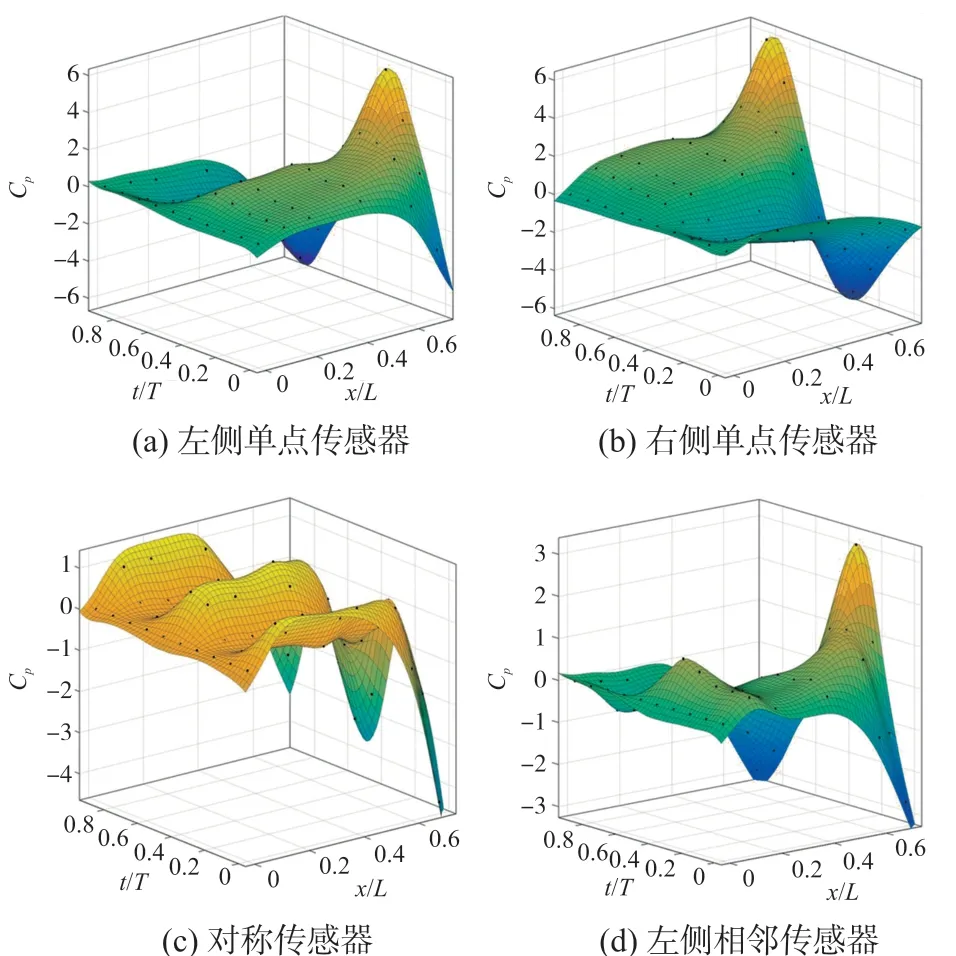
图3 各测量模型时空分布

图2中随着云图颜色越深，流场压力越大，可看出，尾鳍附近存在高压区，鱼体同一侧从尾部到头部压力逐渐减小，鱼体两侧流场交替出现高压区和低压区，具有时空对称性。

从图3(a)和3(b)中可以看出单点传感器得到的压力系数具备时空对称性。从图3(c)和3(d)中可以看出，去掉流场常量的影响后，相邻传感器和对称传感器相比于单点传感器对压力系数波动有一定的抑制作用，图3(c)所示的对称传感器所得到的压力系数在空间和时间上的分布更为均匀。

图4为两个摆动周期部分单点传感器和相邻传感器测量值随时间变化曲线。压力系数周期与鱼体波动周期相同。图4(b)中关于鱼体中轴线对称的一对单点传感器模型测得的压力系数相位差相当于半个摆动周期，鱼体同侧的单点传感器相位差基本为零。图4(c)中单点传感器压力系数波动幅值从鱼体头部到鱼体尾部逐渐增大。图4(d)所示的相邻传感器压力系数时域曲线波动幅值比单点传感器低一倍左右。

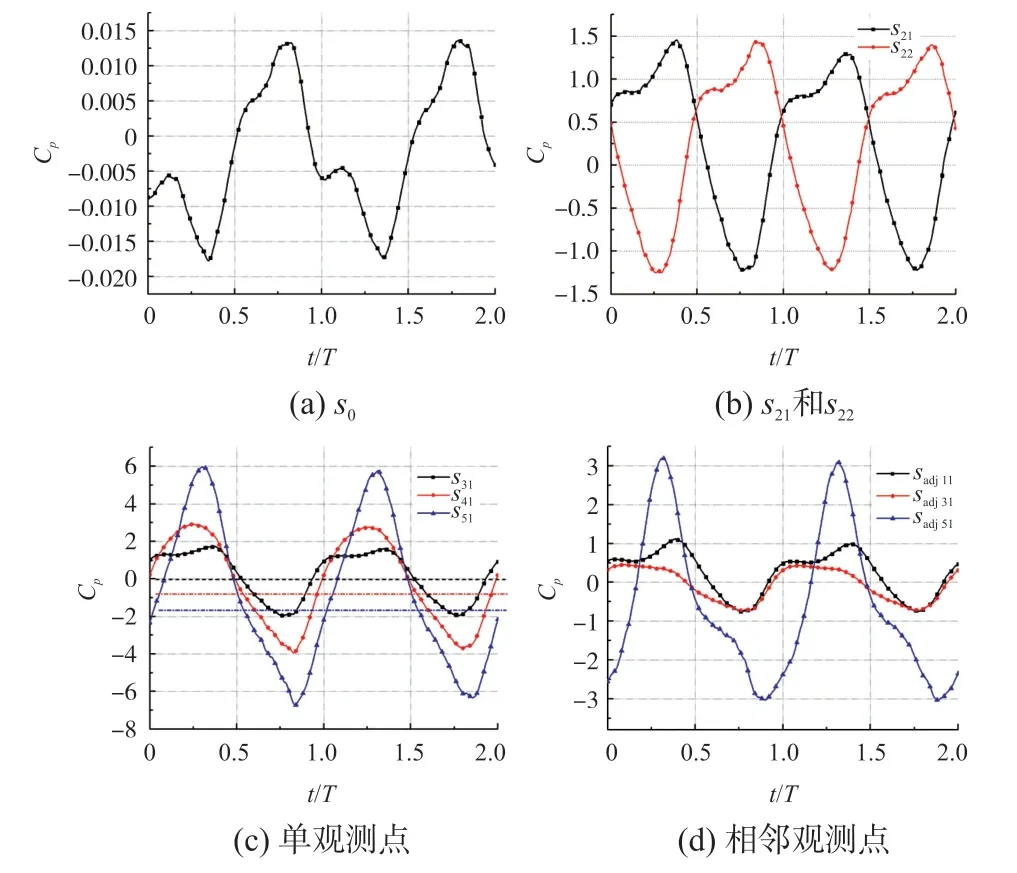
图4 各测量模型测量值随时间变化曲线

3.3 不同流场流速机器鱼体表压力特征

设远场流速范围为0到2 m/s，鱼体摆动频率为1 Hz，鱼首攻角为2°，计算不同流速流场条件下各测量模型监测的压力系数，结果如图5所示。

各测量模型测得的压力系数Cp基本是远场流速V∞的二次函数，在指定的流场参数范围内具备单调性，图5(a)、5(b)和5(c)所示的单点传感器测得的压力系数在流速为0.6 m/s到1.2 m/s区间内有明显波动。本文分析采用“网格重构”法构建动网格技术，重构时造成数值计算伪扩散，从而形成鱼体表面压力的波动，可以视作误差处理。

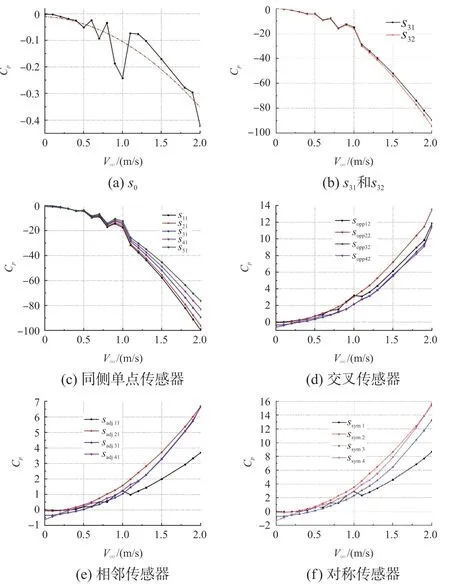
图5 压力系数Cp与来流速度变化曲线

由于消除一定误差以及流场常数的影响，图5(d)、5(e)和5(f)所示的组合传感器模型测得的压力系数相比于单点传感器更为平稳。

为了评价四种测量模型各测点测量值离散程度，绘制图6所示的四种测量模型各测点压力系数标准差随远场流速V∞变化趋势。随着远场流速V∞增大，单点传感器和交叉传感器各测点测量值标准差迅速增大，相邻传感器和对称传感器测量值相对平缓，更适合处理远场流速变化剧烈的流场环境。

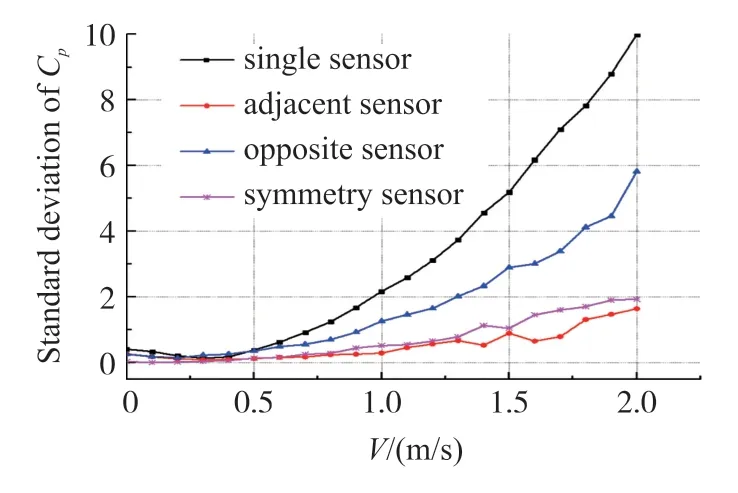
图6 不同流速下压力系数的标准差

3.4 不同攻角机器鱼体表压力特征

设远场流速V∞＝1 m/s，攻角范围为－16°到16°，鱼体摆动频率为1 Hz，各测量模型得到的压力系数如图7所示。

从图7的曲线趋势上看，压力系数Cp和攻角α之间呈高于两次的函数关系。图7(a)和图7(b)所示的相邻传感器和单点传感器在指定攻角范围内不具备单调性，其中后者在攻角为0两侧单调性相反，图7(c)和图7(d)交叉传感器和对称传感器测量模型在全域上具备单调性。

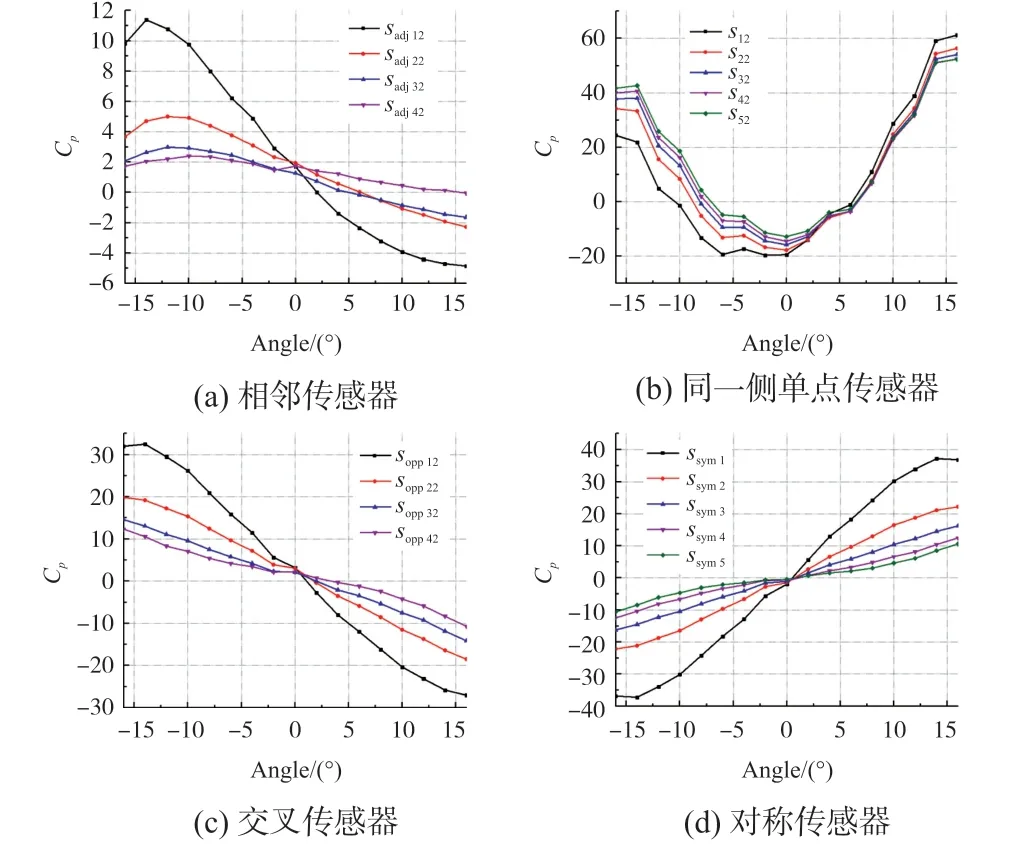
图7 压力系数Cp与攻角关系曲线

从数值波动的角度来看，图7(a)、7(c)和7(d)所示的相邻传感器、交叉传感器以及对称传感器测量数据比单点传感器平滑，交叉传感器和对称传感器可以利用鱼体两侧信息从而判断攻角的正负。

根据图8所示的不同测量模型测量值标准差随攻角变化曲线来看，无论是迎流侧还是背流测，相邻传感器和单点传感器标准差较小，对称和交叉传感器测量值标准差随着攻角增加迅速增大。对于攻角波动较大的情况，例如机器鱼做复杂曲线运动，此时可以用交叉或对称传感器预测攻角正负，用相邻传感器测量具体数值。

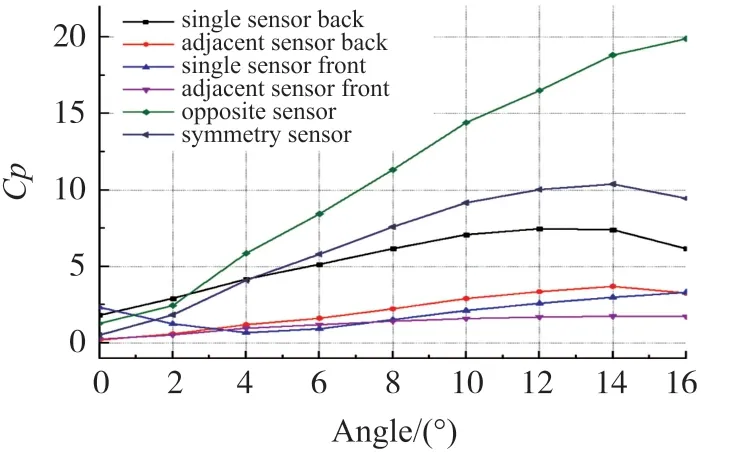
图8 不同攻角下压力系数的标准差

3.5 测量模型输出值回归方程

根据上述分析，鱼体摆动频率一定的情况下，鱼体体表压力是远场流速V∞和攻角α的函数。在CFD计算的基础上拟合来流场参数及波动参数与体表压力系数之间关系，设压力系数函数为Cp(V∞，α；i)。

根据第3.1和3.2节分析，以式(10)、式(11)和式(15)为基础可知，在摆动频率f已知时，体表压力系数可近似视为关于攻角α四次和远场流速V∞二次的函数。故本节根据上述计算得到的数据，基于最小二乘法，以V∞和α为变量构建压力系数Cp(V∞，α；i)多项式回归方程。

由于观测点关于鱼体中轴线对称分布，对于单点传感器和相邻传感器只需构建迎流侧压力系数函数即可。设基准摆动频率为1 Hz，以对称传感器ssym3、交叉传感器sopp32以及迎流侧的单点传感器s32和相邻传感器sadj22为例，构建Cp(V∞，α；i)回归模型，结果如图9所示。

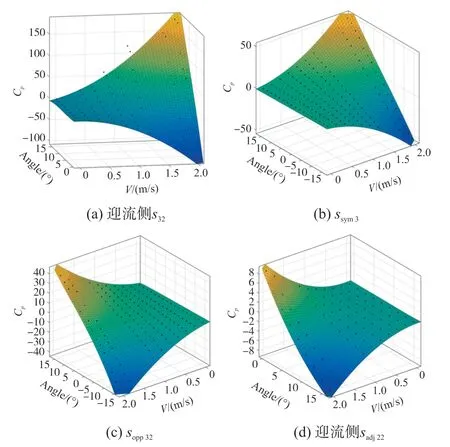
图9 四种测量模型拟合结果

从表1中可以看出采用以式(10)和式(11)形式构建的多项式回归方程可以较为精确地拟合各采样点，相邻传感器拟合效果要优于其他测量模型。

表1 各测量模型拟合度

4 基于SIR粒子滤波的流场参数预测

将3.5节提出的回归方程作为观测方程，估计流场参数，即x＝(V∞，α)。设实际测量值为yi＝βi＋ηi，其中ηi～N(0，σ2i)是第i个测量模型的噪声，呈均值为0，方差为σ2i的高斯分布，不同测量模型之间的高斯噪声互相独立，定义y＝(y1，y2，…yN)为各测量模型所测量值的集合，则流场参数x的后验概率为

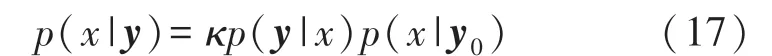
式中，κ为归一化因子，p(y｜x)为似然函数，p(x｜y0)为先验概率分布，设为均匀分布。

为了融合多个测量模型所获得的信息，采用多元高斯分布，对于单个测量模型其似然函数为

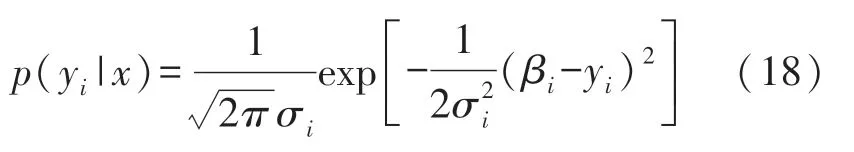
由于各测量模型高斯噪声互相独立，因此流场参数x的后验概率密度为

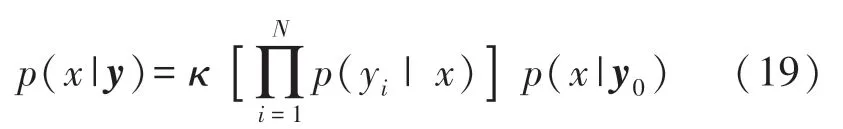
则系统的预测方程为

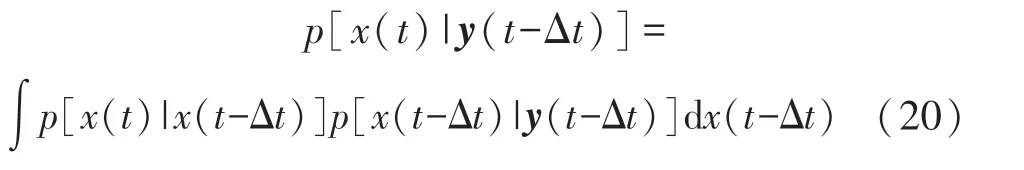
系统的更新方程为:

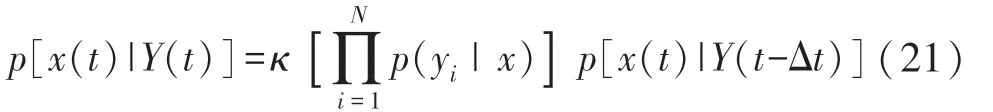
式中，Y(t)＝{y(t)，y(t－Δt)，…，y(0)}，设先验概率的初始条件p(x(0)｜Y(－Δt))为高斯分布。

设远场流速和攻角呈正弦变化，其中远场流速波动幅值为0.5 m/s，攻角波动幅值为1.5°，周期均为2 s，即:

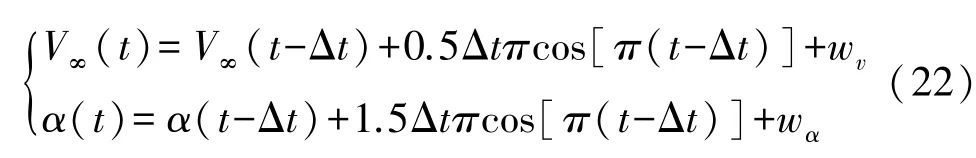
观测方程为:

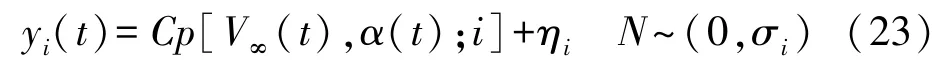
根据式(20)和式(21)定义的预测模型，应用SIR粒子滤波预测流场参数，即远场流速V∞和攻角α，测量模型各测点获取的压力系数为观测量，通过数值计算得出，远场流速V∞由入口速度给定，攻角α由机器鱼自身转动设定，粒子滤波相关参数见表2。

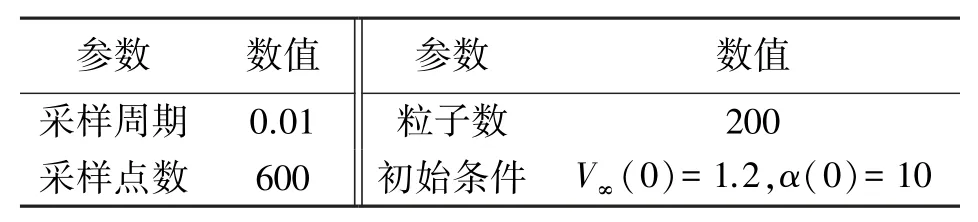
表2 粒子滤波参数

为去除测点位置带来的影响，选取s32、sopp32、ssym3和sadj32四个同一位置处的各测量模型输出的回归方程作为观测方程，重复试验50组，设机器鱼摆动频率为1 Hz，仿真时长6 s，仿真结果和对应的偏差曲线如图10和图11所示。

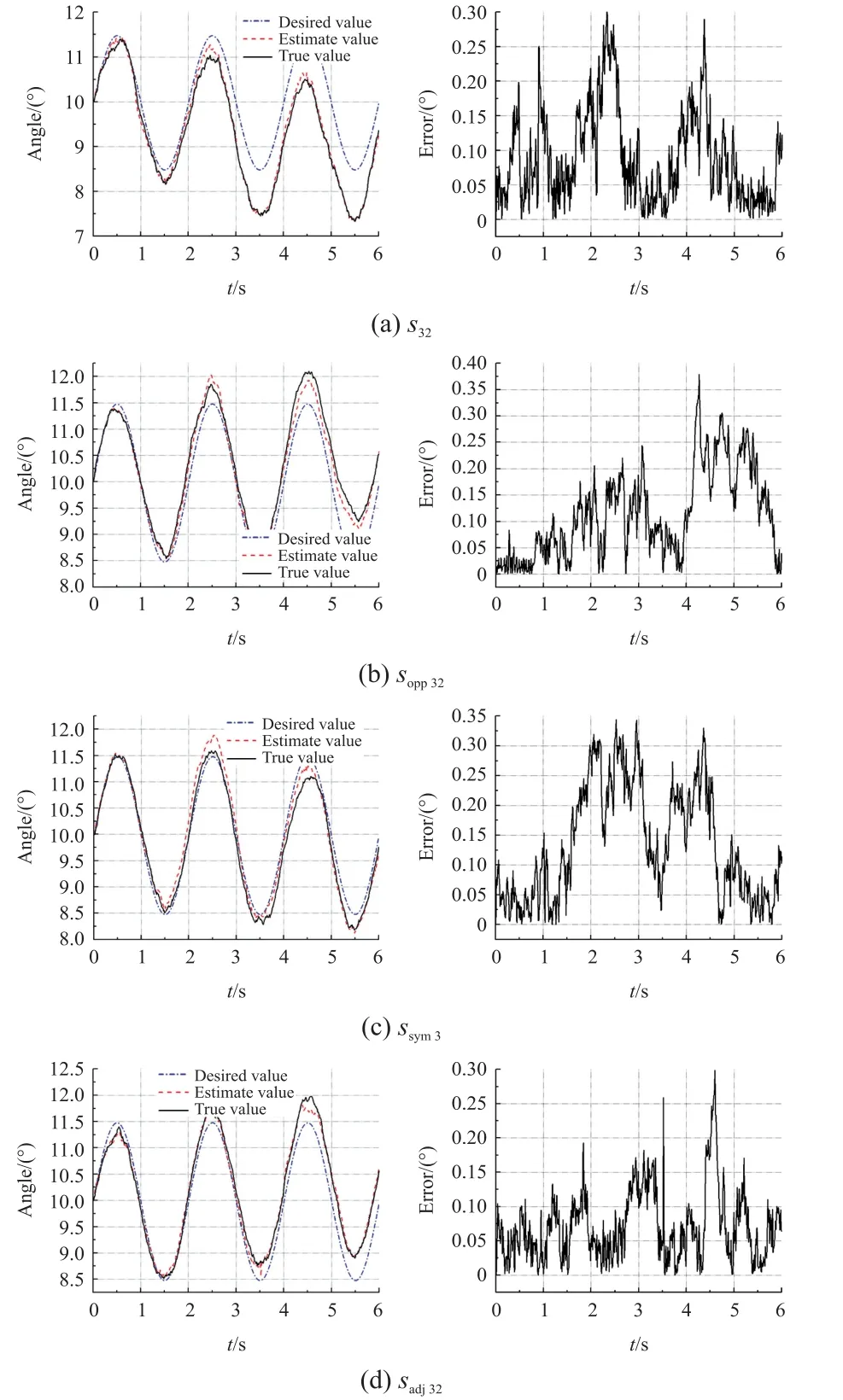
图10 攻角粒子滤波预测效果和偏差曲线

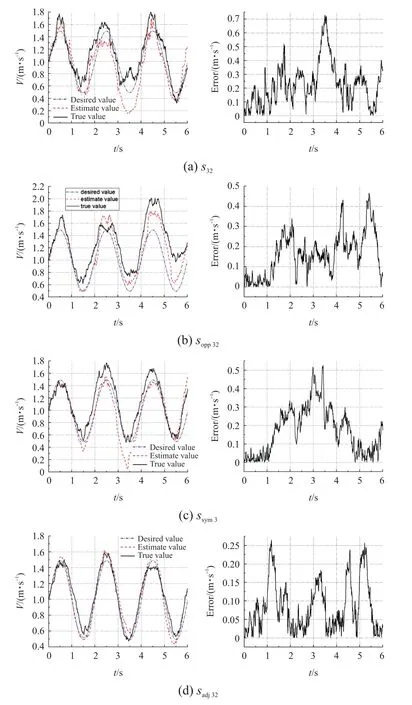
图11 远场流速粒子滤波预测效果和偏差曲线

从图10和图11中可以看出，四种测量模型输出结果均可以较为准确地预测流场参数，预测结果基本跟随真实状态。根据偏差图，在攻角α的估计上四种测量模型的偏差基本一致，对于V∞的估计上相邻传感器偏差最小，交叉传感器和对称传感器次之，单点传感器最大。由于相邻传感器、交叉传感器和对称传感器三种测量模型考虑鱼体表面两个位置的压力系数，一定程度上抵消了部分流场噪声。

为评估多传感器组合应用对流场参数的估计效果，以相邻传感器sadj12、sadj22，sadj32和sadj42为例组合预测。为反映位置因素对观测产生的影响，从鱼首到鱼尾依次加大测量噪声，仿真计算50次，预测效果和偏差曲线如图12所示。计算多传感器组合应用与相邻sadj32传感器预测偏差的绝对平均偏差，结果如图13所示。

将图12与图10(d)和图11(d)对比，两者在对远场流速V∞的估计上精确程度相近，但较大提升了对来流角度预测精度。从图13中可以看出两个参数预测上多传感器组合应用的稳定性较单一传感器略有提升。

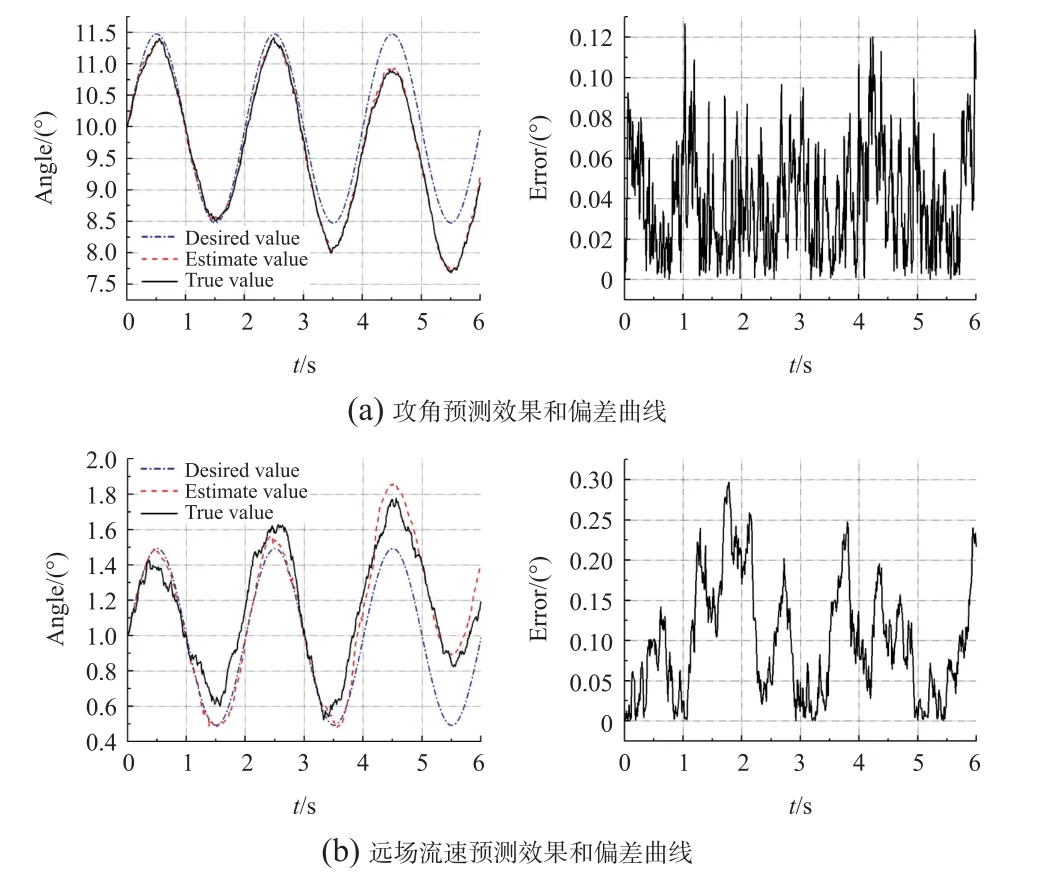
图12 多传感器组合预测流场参数

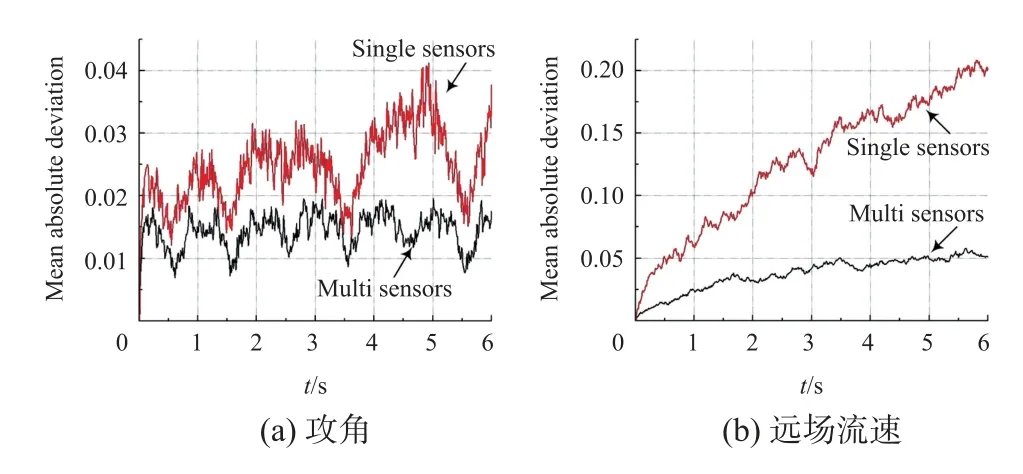
图13 流场参数预测偏差的平均绝对偏差

5 结论

本文结论如下:①以势流理论和伯努利方程为基础分析得到Joukowski对称翼型表面压力与远场流速、攻角和摆动频率相关，并给出具体表达式；②在外包络线为Joukowski对称翼型的二维多关节机器鱼基础上建立四种测量模型并用CFD技术分析，各测量模型优缺点，建立回归方程。综合来看，相邻传感器模型测得的压力系数效果较好；③以SIR粒子滤波为基础的流场参数预测仿真表明所建立的测量模型可以实现对远场流速和攻角的预测。多个测量模型融合后预测效果的平均绝对偏差小于单个测量模型预测结果。

本文提出的方法可以预测较为宽阔的区域的远场流速和攻角，为多关节机器鱼的流场适应性控制提供信息，也为多关节机器鱼探测复杂流场环境方法提供解决思路。