“偿二代”背景下上市保险公司的动态监管研究——基于股票市场信息数据

刘余庆 复旦大学经济学院

本文针对目前我国第二代偿付能力监管体系（简称“偿二代”）监管下的不足，拟用KMV信用风险测度模型及上市保险公司的股票市场价格数据来预测保险公司的违约概率。首先，对KMV模型进行适合我国上市保险公司的修正：1.将限售股纳入股权价值的计算，2.上市公司违约点公式修正为DPT=STD+0.5×LTD+0.8×PR。其次，利用四家A股+H股上市的保险公司（中国太保、中国人寿、中国平安、新华保险）2012—2019年八年相关数据进行实证分析，并检验其有效性。实证结果证明，利用修正KMV模型估计出来的上市保险公司违约距离DD）可以作为中国银保监会监管保险公司的一项重要指标，且因其具有前瞻性，可以满足现阶段我国保险业监管的需求。

一、引言

我国保费收入已经位列世界第二，但以往规模导向的监管制度下行业粗放式发展也带来了投资端资产荒、资产负债不匹配等问题。新经济形势下，保险业承担着更加沉重的风险防控工作压力。当前保险监管的力度相对较弱，与新形势下沉重的风险防控工作负担形成了鲜明的对比，行业风险管控能力显然无法适应行业发展形势，需强化对部分偿付能力风险的重视，通过有效手段切实强化对寿险公司偿付能力的监管力度，使其满足风险防范的需求，更好地顺应行业改革发展形势。“偿二代”在2016年应运而生，采用国际通用的“三支柱”框架，即资本充足要求、风险管理要求、信息披露要求，利用17项监管规则体现“定量监管、定性监管、市场约束”的市场规则要求。

但“偿二代”监管仍有不足之处，权威资料显示，国内一些未挂牌交易的保险企业由于偿付能力不达标而被勒令退出市场，现有监管方法是分析信用的历史情况，可持续性相对较弱，且测度的样本单一，过分依赖样本数据，数据更新的时效性不足，变量选择过于主观，对违约概率的估测准确性较低等问题广泛存在。这就决定着唯有系统而全面地探究保险公司信用风险度量以及监管的问题，才能为保险行业经济的可持续发展提供不竭动力。本文选取KMV信用风险测度模型，从我国基本国情入手，对KMV模型做出了相应调整，以财务信息以及资本市场信息为依据就违约距离进行计算，并以其为动态指标对保险企业偿付能力监管情况进行评价，且进一步检验其适用性与有效性。

二、文献综述

KMV模型发布于1993年，主要通过期权定价模型计算上市公司的违约概率，进而量化分析上市公司的信用风险。目前，学术界在分析KMV模型时，一部分学者验证了KMV模型的有效性，并在不同的行业或领域中广泛推广KMV模型，验证在这些行业或领域中KMV模型的有效性；也有一部分学者探索了该模型在评估信用风险时存在的局限性，并通过其分析结果有效修正模型，并验证了修正后模型的有效性。

从国外研究看，1993年起，国外学者就陆续关注到了KMV模型。如JeffreyR.Bohn（1998）、PeterCrodbi和JeffBohn（2003）等，利用KMV模型对上市公司信用风险进行了评估。M.Stein（2000）、Kealhofer和Kurbat（2001）等对信用风险评估方法进行实证比较分析，证明了KMV模型是更好的评估方法之一；亦有不少学者如Lu（2008），将KMV模型中的假设条件放宽，进一步拓宽了KMV模型的适用范围。

国内对KMV模型的研究虽落后于国外，但早在1998年，国内的学者就已经开始关注KMV模型，并从我国国情出发对其进行了相应的研究。如王琼（2002）、吴冲锋和程鹏（2002）、赵建卫（2006）等主要阐释了传统KMV模型的理论和定义，验证了KMV模型的有效性；李金亭（2009）、陈楷（2012）、姚珊（2015）、郭靖（2016）等结合我国相关行业修正了KMV模型中的部分参数。

与现有研究相比，本文的主要贡献在于：构建了适应我国寿险公司实情的修正版KMV模型，并利用四家上市保险公司2012—2019年八年数据进行计量估计，并且在“偿二代”背景下对其有效性进行检验。

三、KMV模型

KMV模型是基于莫顿模型的基本思路，以市场数据与财务报告为违约概率的主要来源渠道。该方法彻底终结了仅以财务数据进行信用风险度量的时代，其原因在于市场价格与企业未来发展走向间的关联更为紧密，遂伴随KMV模型的应用，信用风险度量的科学性随之提升。

（一）KMV模型的基本思路

KMV模型主张不考虑负债差异的情况下，债务人资产市场价值是影响贷款信用风险的决定性因素。然而，资产并未真正意义进入市场，因此无法直接判断资产的市值。出于此种考虑，该模型从一个新的角度入手进行贷款问题分析，以借款企业所有者为着眼点就贷款归还加以分析。模型的核心思想在于：以公司资本为标的资产，也就是把所有权权益视为看涨期权，将负债作为看跌期权，公司价值满足几何布朗运动的特征。就普遍情况而言，公司资产市场价值（Va）与企业负债账面价值（D）发生偏离的情况下，会有违约情况发生。违约距离（DD）代表企业资产市场价值期望值相距违约点（DPT）的距离，该指标与违约发生概率存在反向关联，即距离越大，违约概率越小；反之则违约概率越大。

KMV模型假设未来特定时期内，上市保险公司预期资产价值满足正态分布。基于图1能够发现，当相较于公司债务账面价值，预期资产市场平均价值明显更低时，公司违约情况将会发生。通过图1还可以看出，一年后公司资产价值分布曲线与债务账面价值曲线两者所产生的部分面积便为公司的预期违约概率（EDF）。

▶图1 KMV模型违约距离图

（二）KMV模型的求解过程

预期违约概率（EDF）的计算共分为三步：第一步，对企业的市值及其波动性进行确认；第二步，就企业预期价值以及违约点进行估测；第三步，预期违约概率（EDF）的求解。

（1）计算公司的市场价值VA及其波动率σA

公司出于保密性的考虑，对KMV具体形式采用了不披露政策。我们往往将函数f替换为Black-Schole公式。

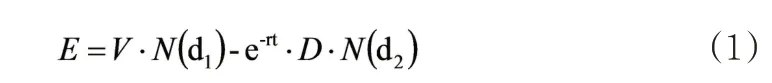
上式中，E表示股权的市场价值；V表示公司资产的市场价值；表示正态分布累积概率函数；r、t分别代表无风险利率与信用期限；D表示负债的账面价值。式中：

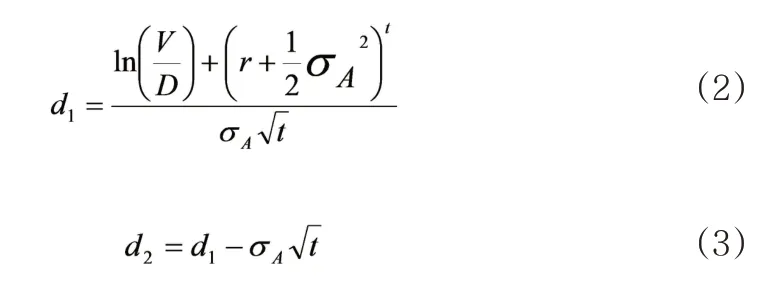
对公式两边进行求导，可得：

将两个方程联合在一起，两个求知数，可计算出VA与σA。

（2）违约距离的求解

通过大量实证分析证明，若满足流动负债和长期负债一半的总和与公司价值相等的条件，信用风险临界点的发生概率最高，即DPT=TD+0.5×LTD，该式中STD与LTD分别表示短期负债与长期负债。

违约间距与资产价值的比值即为违约距离DD，可表示为：

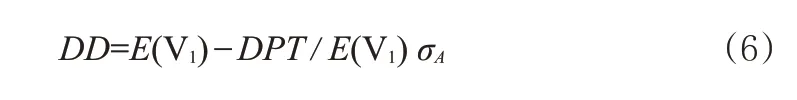
（3）对预测违约概率（EDF）进行求解。

若资产价值满足正态分布，则从理论上讲其计算公式应为：

上式中：EDF——上市保险公司的违约概率；

N（－DD）——违约距离DD的正态分布函数。

（三）适应我国上市寿险公司KMV模型的修正

受国内资本市场特殊性的影响，KMV模型不适宜直接应用于国内上市保险企业进行信用风险的度量。这就决定着在KMV模型应用前，应从我国基本国情出发，与保险公司的特征进一步结合，就模型中部分特定参数进行修改，以期提高上市企业信用风险识别的客观性与准确性。

1.公司股权价值的修正

股权分置改革在国内上市企业内取得了显著的成效，然而限售股依然存在，所以本文认定限售股与流通股的总和为公司股权价值，为研究的严谨性提供了保障。本文选用了诸多文献采用的修正方法，即以单股净资产与限售股股数之乘积为限售股市场价值。可将公司股权价值（VE）的计算公式表示为：

2.违约点DPT的修正

KMV模型定义的违约点DPT是否适用于国内上市企业还有待商榷。在笔者看来，上市企业始终承担着沉重的短期负债偿还压力，我们应效仿西方发达国家，对短期负债也作考量。所以研究的核心转变为长期负债在DPT中所占比重的大小。这一情况下必须有效兼顾保险公司的独特性。投保人支付的保费是保险公司经营收入的主要来源，而保险公司的营业支出则是以保险事故发生时公司基于投保人的具体情况对其所作出的赔偿为主。为尽量满足未来可能发生支付的资金需求，保险公司应充分做好保险责任准备金的筹措工作。保险责任准备金实则为企业负债，保险公司为保证保险职责履行的及时性需具备等值于保险责任准备金的资产，为职责履行提供保证。所以相较于其他行业而言，保险公司的资产负债比明显更高，这就决定着上市保险公司以KMV模型进行信用风险度量的过程中，不仅要对保险责任准备金进行系统而全面的考量，更应结合实际对违约点作出调整。

以我国众学者的相关研究资料为依据，与所积累的实践经验相结合，可将保险公司负债进一步划分为三个部分：（1）流动负债，必须注意到其进一步包含未到期责任准备金与未决赔款准备金两个部分；（2）长期责任准备金，其为涉及寿险业务的保险公司所特有；（3）其他非流动负债。

本文以2009年周洗帆研究所提出的假设为依据，即如果受某一风险因素的影响，保险公司需承担的赔付率提高20%，那么其保险责任准备金将面临偿付风险。本文以该假设为前提将计算违约点的办法调整为：

上式中：STD代表保险公司以短期责任准备金为代表的流动负债；LTD代表除短期责任准备金以外的其他流动负债；PR则表示长期责任准备金。

3.违约距离DD与违约概率EDF映射关系的修正

违约距离DD表明与违约点间的距离远近，从某种角度来讲，这也是评价企业违约概率的关键指标。若违约距离较小，则表明公司极易违约，即违约概率较大；反之，则违约概率较小。与欧美等西方发达国家对比而言，市场经济在国内的发展相对缓慢，现阶段很难建立与我国本土上市企业相匹配的违约距离与违约概率的相互关系。本文在就违约概率进行评价时是以违约距离为主要指标，此处并未对EDF作深入考虑，这是为匹配国内上市保险公司的客观情况而对模型作出的调整。

四、基于修正KMV模型的实证分析

（一）样本选择

基于前文分析能够发现，本文以四家上市保险公司为研究样本，分别为中国太平洋保险（集团）股份有限公司（股票代码：A股601601和H股02601）、中国人寿保险（集团）公司（股票代码：A股601628和H股02628）、中国平安保险（集团）股份有限公司（股票代码：A股601318和H股02318）、新华人寿保险股份有限公司（股票代码：A股601336和H股01336）。因本课题研究对象是“偿二代”背景下的我国人寿保险公司，故选取在A股市场挂牌的公司作为样本，对以中国人保为代表的仅在H股上市的保险公司不作深入分析。

本文是通过Wind数据库搜集的上市保险公司的财务信息、股权结构以及股价。股价与指数的时间节点均始于2012年初，终于2019年底（由于新华人寿保险股份有限公司于2011年底上市，因此选择从2012年1月初开始）。

（二）修正KMV模型中参数设定

1.无风险利率r的确定

国内上市企业的信用风险评估过程中，并不具备规范化的无风险利率选择标准，且因国内利率管制相对严格，因此本文的无风险利率是选择中国人民银行一年期定期存储利率的加权平均值。因中国人民银行一年期定期利率的不稳定性较强，银行或许会数次进行调整，所以本文对一年内的数次利率进行加权平均计算，并以其为无风险利率r，详见表1。

2.上市保险公司的负债面值D与实际期限t的确定

本文是通过估测的方法以上市企业年度财务报表数据为依据对负债面值进行估量，负债期限为1年，即t=1。

3.股票年波动率的计算

目前全球众多学者均对股价波动率的计算方法作出了深入研究，且取得了累累硕果。本文将原模型中的股权价值波动率替换为流通股股票价格波动率。所谓股票价格波动率，即对股票价格在未来特定期限内发展方向的不确定性的评价，若股票价格波动率持续提高，则代表未来特定期限内该股票价格并不稳定，发生变化的概率较高。在该课题的研究过程中笔者选用了历史波动率法，也就是以研究样本前一年股票价格波动情况为依据，对后一年股票价格波动率的情况进行估算的方法，对未来一年上市企业股权市场价值的波动情况进行估测。基于日收盘价可对股权价值日标准差σ′进行计算。假设一年内交易日共250天，遂能计算出年收益波动率σE。其表达式为：

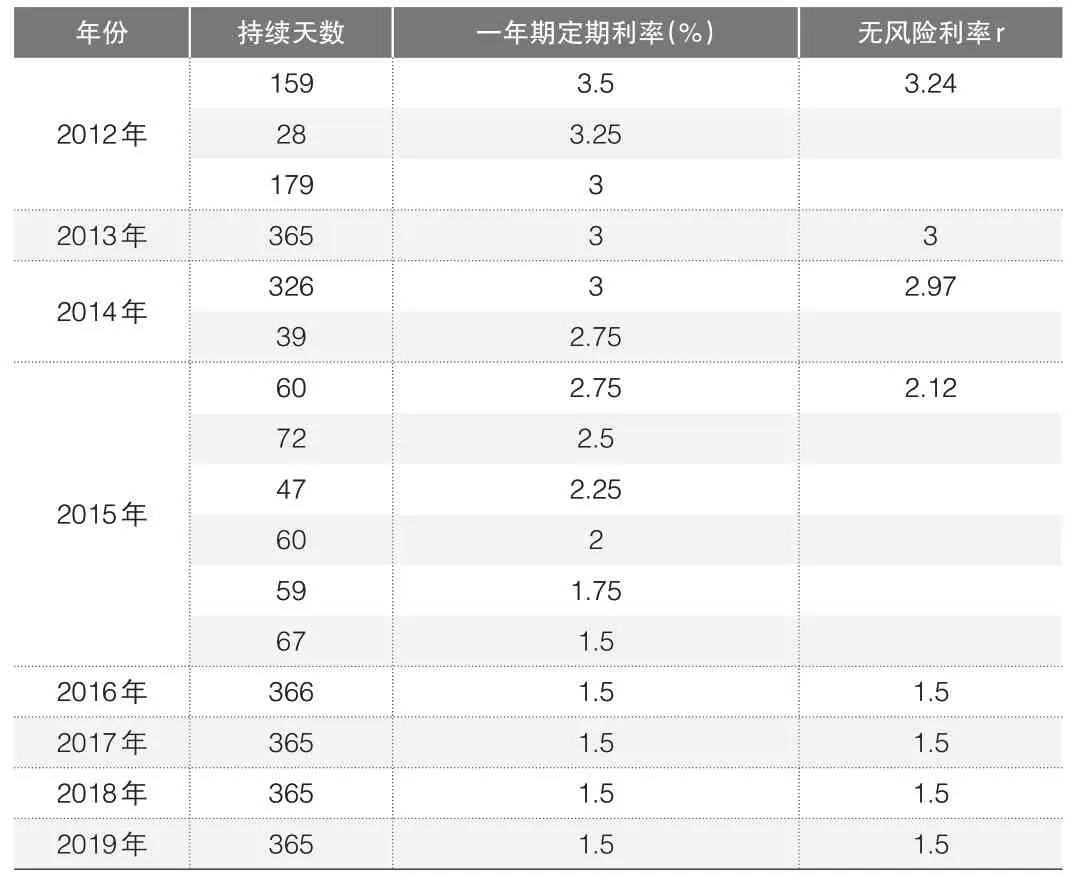
▶表1 无风险利率r

另外，BSM模型假设上市企业股票价格满足正态分布的特征，则股票价格对数收益率的计算公式应为：

上式中：Si、Si-1分别表示复权当日以及复权前一日的股票收盘价。据此可对企业股价的日标准差进行计算，进而求解出股价的年标准差。

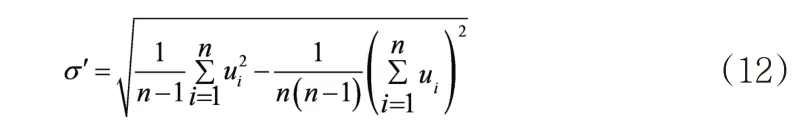
（三）修正KMV模型实证过程

以上文KMV模型的实证分析方法为依据，以中国太保的样本数据对违约距离进行估测，且通过对比分析法进一步研究相关结果。本文先以中国太保为例计算违约概率。

第一步，计算中国太保股票年收益波动率σE。运用公式（10）、（11）、（12）以及STDEV函数、AVERAG函数对股票的日标准差以及收益率进行求解。以上述公式为依据，与各相关数据相结合，可计算出中国太保的收益日标准差σ′为0.017，那么中国太保2019年的股票年收益波动率σE为0.262。

第二步，计算中国太保的股权价值VE。运用修正过的公式（8）估算股权价值VE：用中国太保2019年一年中所有交易日的收盘价的平均值乘以相应流通股的股数（A股和H股分别计算）加上中国太保这一年每股净资产乘以限售股的价格，即可得到中国太保2019年的股权市场价值VE=293767。

第三步，计算中国太保的违约点DPT。运用修正过的公式（9）

PT=STD+0.5×LTD+0.8×PR，查阅2019年中国太保相关财务数据得出中国太保2017年的违约点DPT为1114709。

第四步，运用公式（1）、（2）、（3）、（4）利用BS模型，将前面所计算出的股票年收益波动率与股权价值代入MATLAB软件，依靠相关迭代程序对2019年中国太保的公司市值以及市场价值波动率进行计算，其中公司市值VA为1391881、市场价值波动率σA为0.06。

第五步，对中国太保违约距离DD的计算。上市企业违约概率的评价离不开违约距离DD，违约距离与违约概率间存在反向关联，即距离越大，违约发生的可能就越小。因此，在“偿二代”背景下，上市保险公司以监管者为代表的各利益主体均能依托于KMV模型对企业违约距离进行求算，并将违约距离与相关决策相挂钩，以达到信用风险规避的目的，有效保证企业利益不受侵害。

根据第四步计算出来公司市场价值VA和公司市场价值波动率A，运用修正过的公式（5）、（6），得出中国太保2019年的违约距离D=3.60。

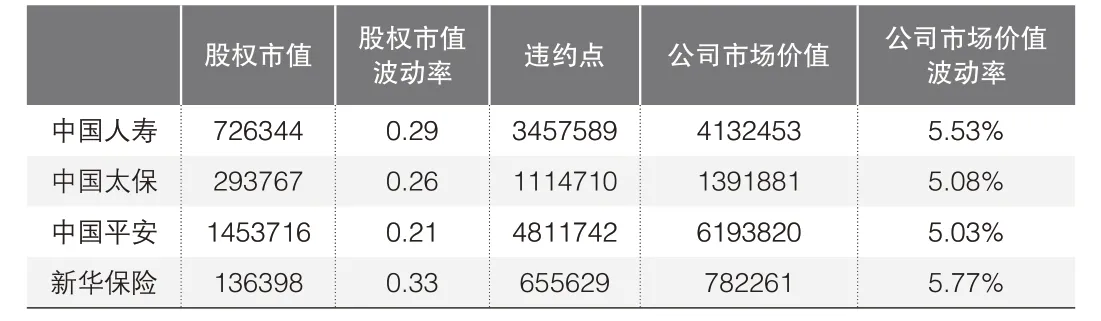
▶表2 2019年四家上市保险公司的各项指标（单位：百万元）

由表2可见，四个研究样本中公司市场价值最大的企业为中国平安，新华保险的市场价值波动率大，意味着新华保险经营不确定性相对较大，所承担的风险成本也相对较高，所以四家样本公司中信用风险预测难度最大的亦当数新华保险。依照由大到小的顺序对2019年四家样本公司的市场价值波动率进行排列，即新华保险、中国人寿、中国太保、中国平安，所以2019年信用风险度量波动性最显著的样本公司应为新华保险。

为了更好地比较四家公司之间的信用风险程度，将四家公司的数据代入第五步，求得2019年四家公司的违约距离DD，中国人寿违约距离DD为3.21、中国平安违约距离DD为4.44、新华保险违约距离DD为2.81。同理可得2012—2019年四家上市保险公司违约距离DD及其均值情况见表3。

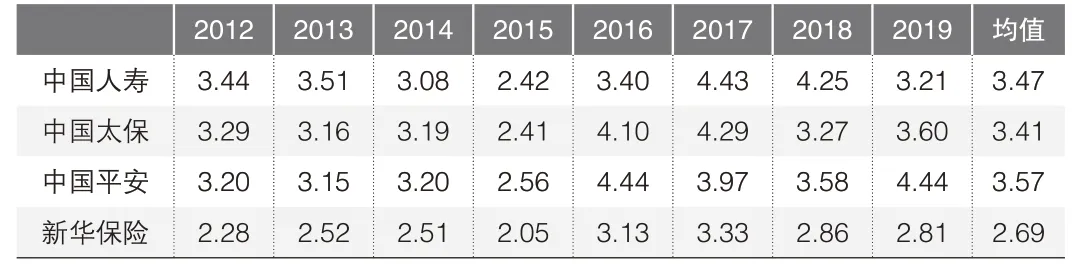
▶表3 2012—2019年四家上市保险公司的违约距离DD

（四）实证结果分析

通过对KMV模型计算出的2019年四家上市保险公司的违约距离比较，可以看出中国平安的违约距离最大，中国太保次之，新华保险以2.81违约距离最小。然而基于有关学者采用KMV模型对国内上市企业进行的实证分析结果能够发现，整体来看国内上市企业违约距离在4以上的业绩水平相对较好，风险的稳定性较为显著，违约概率相对较低，上市保险公司亦是如此。从2019年来看，中国平安处于一个信用风险相对稳定的环境，新华保险、中国人寿、中国太保则处于信用风险相对较大的环境中，违约风险较大。

同时，将2012—2019年四家上市保险公司的违约距离DD变化进行比较，具体情况见图2。

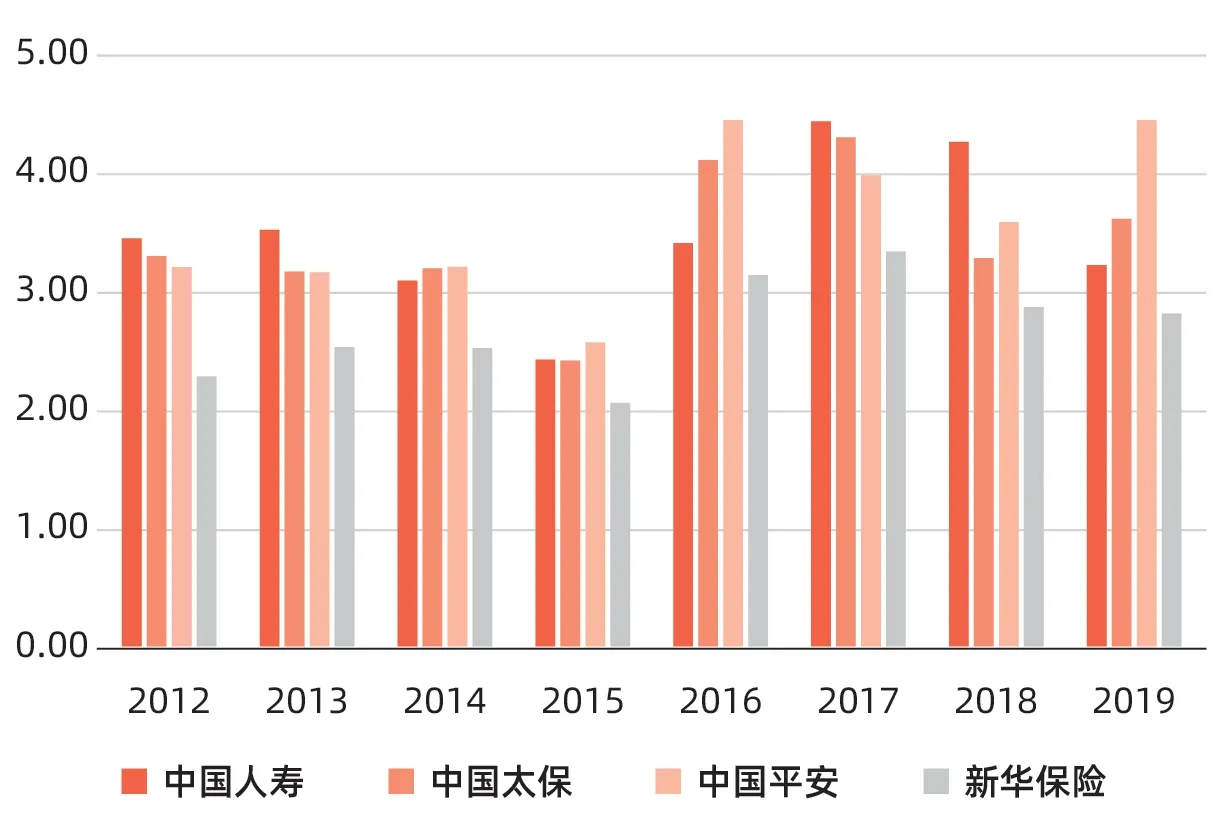
▶图2 四家上市保险公司2012—2019年违约距离变化比较图

基于图2能够发现，2012—2019年间四家样本公司的违约距离变化并不相同，中国平安、新华保险相对比较稳定，中国太保、中国人寿则起伏较大。首先从四家公司8年的违约距离均值来看，中国人寿为3.47，中国太保为3.41，中国平安为3.57，新华保险为2.69，中国人寿、中国平安、中国太保在2012—2019年期间违约概率较小，新华保险则违约概率较大。

从历年违约距离变化来看，中国平安虽然违约距离均值为四家上市保险公司中最大的，但在2015年时中国平安的违约距离低于3，仅为2.56。究其原因，这与2015年我国A股市场巨幅震荡有关，2016—2019年期间违约距离稳步提升。2012—2019年间中国太保、中国人寿的违约距离并非完全不变。经详细分析能够发现，无论是中国太保还是中国人寿，其违约距离的稳定性均相对较弱。

然而以违约距离为重要指标，对中国人寿、中国太保两家样本企业的预测却存在显著差异。首先，2012—2014年间中国人寿的违约距离稳定性相对较强，在2015—2019年期间起伏较大，且2019年中国人寿的违约距离为3.21，较前一年下降1.04。这说明在未来的几年间中国人寿违约风险是异常不稳定的，需要持续关注。其次，从中国太保的违约距离变化来看，2014—2017年中国太保的违约距离存在不断增加的趋势。虽然2018年较2017年有较大幅度的下降，但2019年中国太保的违约距离又有了细微的上升，这也从另一角度说明了在未来至少一年的信用风险预测监管过程中，中国太保所承担的信用风险成本持续增加。相比之下，新华保险的违约距离起伏虽然不大，但违约距离一直是四家上市险企中最小的，需要重点关注。

五、相关结论及建议

本文在“偿二代”背景下系统分析了保险公司的信用风险监管情况，并据此提出了以证券市场信息为动态指标，对上市保险公司进行信用风险的评价与监管，并以国内代表性较强的四家保险公司为研究样本，以其A股与H股的相关数据为研究数据，通过调整后的KMV模型对2012—2019年间国内上市保险企业信用风险度量的适用性以及实效性进行了实证分析。据此发现，KMV模型经相关参数调整后，与国内上市保险公司的客观情况更为匹配，该模型有利于提升“偿二代”背景下上市保险公司的监管力度。此外，调整后的KMV模型能将国内上市保险公司的客观情况基本映射出来，有较强的适应性。

为更好地发挥KMV信用风险模型对上市保险公司的监管，对“偿二代”进行有效地补充，首先，必须完善和发展证券市场。只有保证证券市场的有效性，才能通过KMV模型对上市企业进行信用评估，唯有这样，该模型才能将上市企业的信用情况系统而客观地呈现出来。有效的证券市场为模型所需样本数据的信度与效度提供了保证。然而，因当前我国依然停留在社会主义初级阶段，尚未建立完善的社会主义市场经济体制，证券市场依然存在诸多问题，对KMV模型的客观基础造成一定负面影响，从而干扰该模型的建立以及运行。这就决定了我国应全力推进证券市场的市场化发展，切实提升股市信息披露的规范性，强化市场监管力度，将证券市场的投机概率控制到最低，使企业经营情况能够通过股价客观而准确地呈现出来，进而创造有利于KMV模型运用的金融环境，使其更准确地评价出国内上市保险公司的信用风险情况。

其次，建立信用风险基础数据库。基于前文内容，现阶段我国依然尚未建立完善的上市企业历史违约数据库，进而缺少建立映射关系的必要违约样本，导致无法准确计算违约概率，遂在企业信用风险评价的过程中只能以违约距离为评价指标。只有结合国内以保险公司为主的上市企业客观情况，尽快建立完善的信用风险历史数据库，才能为资本市场信息的现代信用风险评估模型提供有力的数据支撑，进而带动KMV模型预测监管水平的强化，为该度量方法的实际运用奠定基础。

最后，KMV模型作为有效的监管指标，其预测能力极为显著。其将公司市场价值与违约概率直接联系在一起，以公司股权市场价值与负债为依据可计算出EDF值，股权价格信息直接决定着KMV模型的信息水平，通过KMV模型对国内上市保险公司的EDF值进行求解，与动态监管的形势更为匹配。现阶段我国采用了半动态方式进行保险公司监管，基于静态历史数据的分析，可对企业偿付能力建立起相对客观的认识，若公司经营情况相对良好，其实效性以及可行性相对较高。然而保险公司经营存在一定的不确定性，若经营环境的变化超出预期，静态监管方法将毫无意义，甚至产生负面作用。与此同时，受财务报表数据传输时效性不足的影响，有时会发生如下情况：保险公司实际偿付能力已无法满足业务需求的情况下，报表所反映的偿付水平依然相对较高。这就决定了应以股票市场信息为依据，对其中与信用风险相关的内容进行发掘，违约距离DD与违约概率EDF能够使传统监管手段的不足得到有效弥补。

然而，KMV模型的适用存在一定局限性。普遍来讲，该模型在上市企业信用风险评估方面的效果最为显著，然而现阶段国内已成功挂牌的上市保险公司不过六家，在适用于非上市保险公司时，大都需要将模型中一些关键的指标替换为可体现非上市公司实际情况的指标或会计信息，且需依靠对比分析方式对样本企业的期望违约概率进行估测，从某种角度来讲或许会对计算的准确性造成负面影响，进而降低保险公司监管过程中EDF值的可操作性。