一种基于泛函波束成形的传声器阵列优化方法
2021-11-12殷光耀金光灿
殷光耀, 金光灿, 李 锦, 刘 浩
(1 上海工程技术大学 机械与汽车工程学院, 上海 201600;2 迅达(中国)电梯有限公司 亚太研发中心, 上海 201800)
0 引 言
传声器阵列在声学问题上的应用呈现不断上升的趋势,其中对于声源的辨识是传声器阵列的一大重要功能。声源的辨识对于传声器阵列的波束模式十分依赖,而阵列波束模式取决于波束成形算法和传声器阵列的几何阵型。波束成形是用于传声器阵列的一种有效声源辨识的声学成像技术[1〗。目前,波束成形技术在汽车、航空航天、电梯等工业领域中,广泛用于二维、三维噪声源的定位[2]。在二维声源定位中,传声器阵列对声源所在平面进行扫描称之为扫描平面(XY面),扫描平面往往与阵列所在平面平行。二维声源定位法由于只扫描阵列平行平面,所以其只能反映声源映射在扫描平面上的位置而非其实际位置。对于声源与阵列所在平面之间Z方向上的距离大小(声源深度),二维声源定位法则无法进行辨识。因此,当待辨识的声源不位于一个平面,而是具有一定空间体积时(例如:发动机等复杂机器噪声、起落架等航空部件噪声),声源的平面映射并不能准确反映其真实来源[3]。因此,能够实现声源在三维空间上定位的空间映射方法得以出现,波束成形技术的三维应用并不复杂,其实现的方法在于三维网格的应用[4]。三维网格应用也存在一定的实际问题,其中最为突出的是在源深所在维度上声源辨识的分辨率远低于其它维度。
传声器阵列的几何阵型也对阵列声源辨识性能有巨大影响,研究者也进行了大量研究。
二维平面阵列分为规则阵列和不规则阵列。规则阵列有Élias提出的交叉X型阵列,还有网格阵、圆阵、同心圆阵等[5]。规则阵列有着等间距的传声器布局模式,该布局模式下声源频率超过一定限制值(高频声源)后,空间混叠带来的旁瓣加重现象可能会形成栅瓣从而产生“虚声源”。不规则阵列里有常见的多旋臂螺旋阵列,其螺旋臂设计往往是基于确定数学定义的几何曲线[6],通过优化的方法得到的性能良好的随机阵列作为一种不规则阵列也越发得到研究者的关注[7]。不规则阵列在对声场空间采样时能产生更为平滑的结果,因此空间混叠的影响可以保持在可接受的范围内[8]。波束模式除了有旁瓣水平加重现象之外,阵列进行低频声源辨识时,加宽的主瓣波束宽度会减小阵列可以达到的空间分辨率。在对低频声源辨识时,为了提高分辨率,可以通过扩大阵列孔径以保证阵列中的传声器分布离散度更高,从而达到提高低频分辨率的目的[7]。然而,阵列尺寸不能实现无限制的扩大,带来低频分辨率不够高的问题[8]。为了改善传声器阵列的波束模式从而达到提高阵列声源辨识性能的目的,研究者们对传声器阵列进行几何阵型的优化研究,在设计优化过程中自由度过多,使得确定传声器准确的位置变得并不容易[9]。为了得到不规则阵列,一些算法对规则阵列传声器位置进行空间扰动,从而得到性能提升的传声器阵列阵型[10]。基于目标波束模式,将目标波束模式和实际获得的波束模式之间的差值作为目标函数,以搜索目标函数的最小值为目的,对阵列传声器位置进行非线性优化,该优化的实现可以基于遗传算法[11]。由于遗传算法要达到收敛的耗时较多,为了克服耗时问题,对算法的改进也一直被关注[12]。凸优化也是确定传声器优化位置的一种方法[13]。此外,用于全局优化的数值方法(例如:模拟退火结合IBMC法)也可以有效地寻找优化传声器布局形式,来获得更好的阵列波束模式。
本文探究智能优化算法在传声器阵列阵型布局优化中的应用。首先,提出改进的渐开线多螺旋臂阵列设计方案,其中关键几何参数有传声器数目、阵列孔径半径、旋臂数目和渐开螺旋线基圆半径,通过渐开线通用公式描述了各传声器的位置和相对几何关系。这些几何参数可以用来计算优化目标函数值和仿真控制。泛函波束成形公式定义了对扫描平面上任何位置的声源进行辨识时,传声器空间分布形式和阵列波束模式之间的关系。为了使用全局优化算法寻找全局最优解,基于传声器阵列波束模式构建目标函数。最后,寻找最优几何参数组合,构建优化传声器阵列,在此基础上对优化传声器阵列进一步优化,成为一种优化的随机传声器阵列。
1 阵列设计
本文提出的传声器阵列采用多螺旋臂的形式,螺旋臂是环绕阵列中心均匀分布的,引入齿轮齿型设计中常用的渐开线作为螺旋线的线型,将传声器分布在渐开线螺旋臂上。
本文设计的多螺旋臂渐开线式的传声器阵列结构示意图如图1所示,其中红色的部分为基准螺旋臂。阵列设计时需要确定几个参数:阵列最大孔径为D,即最外圈传声器环的直径,其半径表示为rmax;最小传声器环的半径为rb(最小传声器环即形成渐开线的基圆);传声器环的数目为Qn;螺旋臂数目为Na;每个传声器环上的传声器数目为Nm。
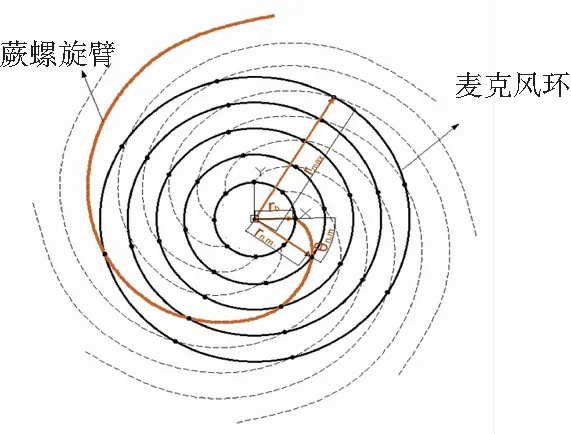
图1 传声器阵列结构示意图
最内部的传声器环上传声器的向径和角度,式(1)和式(2):
r1,m=rb,m=1,...,Nm
(1)
(2)
该环上的传声器为各渐开线的起点,各渐开线由初始渐开线(其起点在基圆圆心右侧的水平位置,并将其作为基准螺旋臂)环绕基圆圆心旋转而来。从第二个传声器环开始,各环传声器向径计算为公式(3):
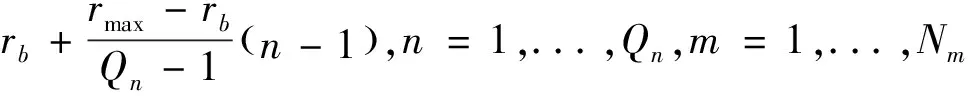
(3)
根据渐开线的规律,以基准螺旋臂为初始位置(基准螺旋臂上的传声器为各环的第一个传声器),可以得出传声器角度为式(4):
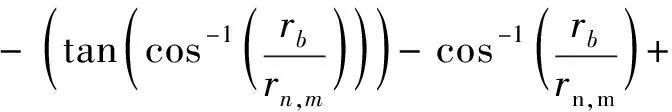
(4)
选定几何参数数值时依次确定阵列孔径和基圆的大小,传声器和螺旋臂的数目,得到最大传声器环和最小传声器环的半径,每个螺旋臂上传声器的数目和传声器环环数,传声器的向径和角度。最内部传声器环的直径很大程度上影响波束模式,直径越小则旁瓣水平越小;直径越大,则主瓣波束宽度越小,阵列分辨率越好。因此,最内部传声器环的直径选择需要根据实际应用需求进行调整优化。
2 泛函波束成形
假设在空间中同时分布着传声器阵列和声源。图2为传声器阵列扫描示意图,为了分析位于Xs处的点声源,使用包含N个传声器的阵列,第i个传声器位置为Xi,选取阵列中心位置X0作为参考点,则第i个传声器处复数值声压P为式(5):
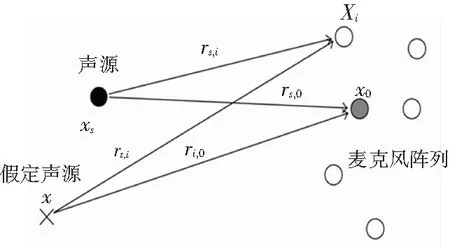
图2 传声器阵列扫描示意图
p(Xi)=a(Xi,X0,Xs)q(Xs)
(5)
a(Xi,X0,Xs)为传递函数,式(6):
(6)
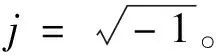
对声源所在平面进行扫描,需要对扫描平面构建网格,依据各个网格点构建扫描矢量,式(7):
(7)
其中,rg,i表示各网格扫描点到各传声器的距离,rg,0表示各网格扫描点到参考点的距离。
传声器阵列的互谱矩阵C可以表示为式(8):
(8)
其中,符号“—”和“H”分表代表取均值和Hermitian转置。
首先,计算阵列互谱矩阵C的特征值分解,式(9):
C=UΣUH
(9)
其中,U是酉阵;Σ=diag(σ1,...,σN)是一个对角矩阵;U中的列向量u1,…,uN是矩阵C的特征向量;Σ中的对角元素是特征值。定义f为一个数学表达式,将C代入得式(10):
f(C)=Uf(∑)UH=Udiag[f(σ1),…,f(σN)]UH
(10)
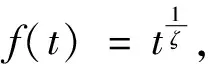
(11)
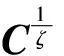
(12)
显然,若ζ=1,则式(12)退化为传统波束成形的表达式;当ζ>1,泛函波束成形在声源处的输出值仍然是声源平均声压值,但在其余位置处输出值将会小于传统波束成形输出值,即旁瓣会衰减。本文关注点在于低频声源辨识,关注的频段主要问题在于过宽的主瓣宽度造成分辨率低,而旁瓣影响并不明显,所以基于二阶(ζ=2)的泛函波束成形算法进行阵列阵型的优化即可。
3 优化过程
本文基于一种改进遗传算法来寻找全局最优解,优化的主要关注点是阵列分辨率不够高的问题,通过优化阵列几何布置,来达到减小阵列主瓣波束宽度的目的,从而提高阵列低频分辨率。当然,旁瓣的影响在优化过程中会保持在可接受的范围内,实际上低频带内旁瓣的影响并不大[14]。量化分辨率的指标参数称为-3 dB主瓣波束宽度,指主瓣峰值以下3 dB处对应的主瓣直径,该参数值越小,则分辨率越好;衡量旁瓣水平的指标为阵列动态范围,即主瓣峰值和最大旁瓣峰值的差值,该参数值越大,则旁瓣相对水平越小。优化过程的目的可以转化成数学形式(13):
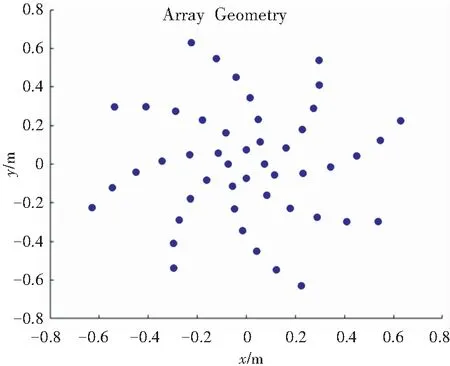
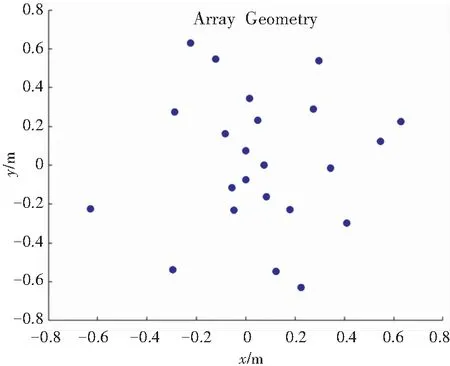
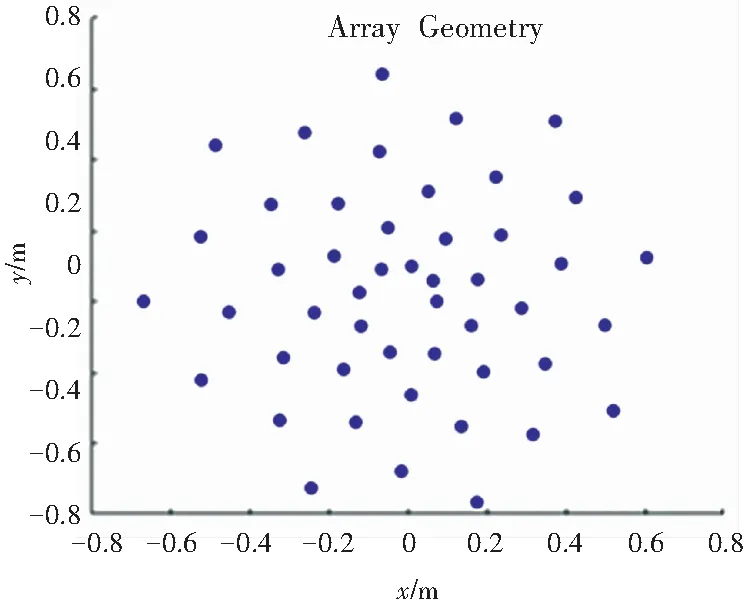
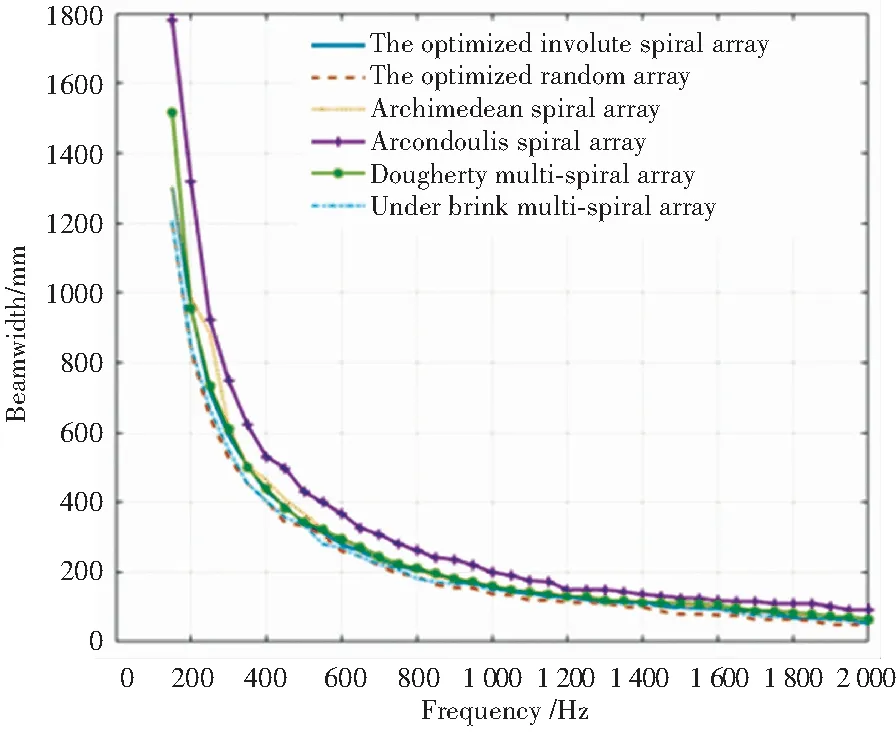
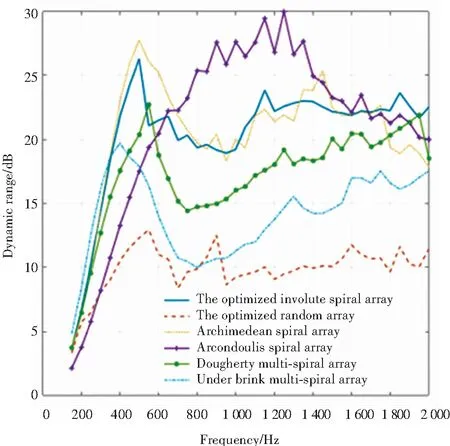
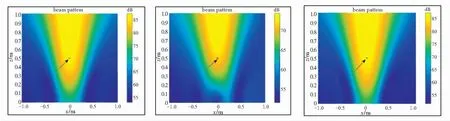
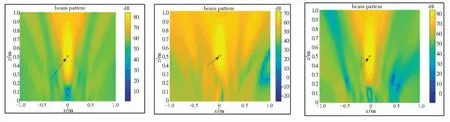
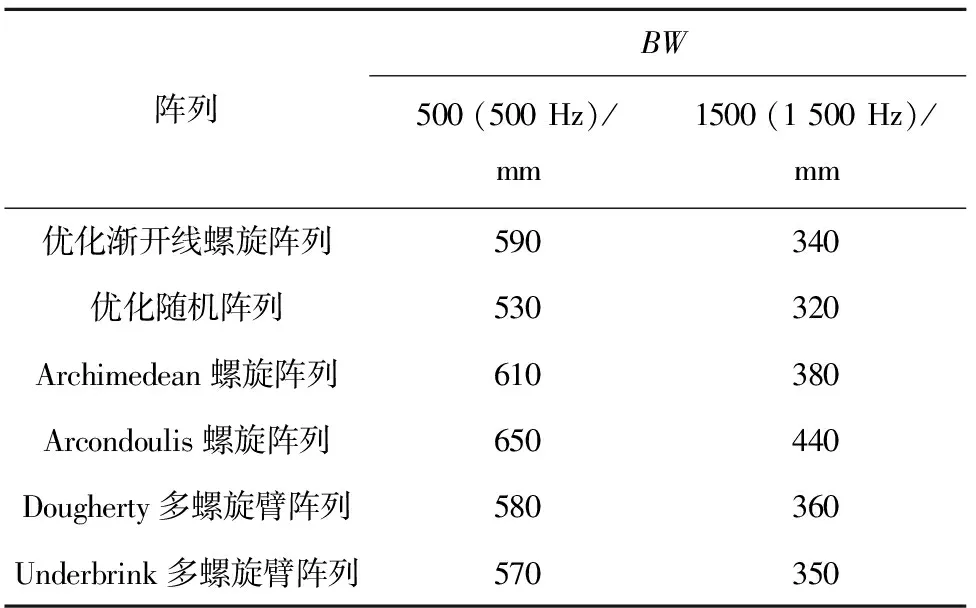
min{Pr}BW-3 dB(f)150 Hz (13) 其中,Pr代表传声器位置向量,包含了传声器的坐标位置。 本文优化的目的是为了寻找一种传声器阵列的几何布置形式,在该阵型下进行特定频带的声源的辨识时,可以获得较好的阵列分辨率。由于阵列在进行低频声源辨识时,波束宽度加宽现象严重,所以本文优化关注的频带范围为150~2 000 Hz。基于传声器阵列波束模式构建目标函数,由于高频率声源辨识时阵列波束模式有更小的主瓣波束宽度,所以将高频波束模式作为目标波束模式,将优化过程中产生的过渡阵型对应的波束模式作为实际波束模式。基于最小二乘法的思想,将上述两者差值作为目标函数计算适应度,式(14): (14) 其中,Pobj为目标波束模式;PFB_iteration为每一步迭代的波束模式;α为调整系数。 从式(14)可知,目标函数值越小,证明每一次迭代得到的波束模式更接近目标波束模式,每一次迭代产生的几何阵型对应的阵列分辨率都在不断提高。在优化过程中,基于一种memetic框架下的改进遗传算法,对上述目标函数进行全局最小值的寻找,并且找出对应的最优传声器阵列阵型几何布置。 在利用优化算法进行寻优的过程中,考虑到实际应用中的空间限制,在传声器阵列阵型的布置中引入一些约束条件,即对传声器布置的边界进行规定。第一个限制条件是传声器位置布置区域的最大范围,这个范围的边界由阵列孔径(最大直径)决定,在优化传声器布置位置的同时需要保证一定的孔径来增加分辨率提高的效果;第二个限制条件是传声器位置布置的最小范围(渐开螺旋线基圆半径);第三个限制条件是传声器的数量,这个条件是为了控制阵列中传声器的成本。基于以上的这些需求,在优化过程中首先引入初始限制条件: (1)阵列孔径的半径取值范围为0.5~1.2 m; (2)形成渐开螺旋线的基圆半径取值范围为0.06~0.12 m; (3)传声器数目取值范围为16~150个。 本文在优化过程中采用一种memetic框架下的改进遗传算法的流程如图3所示。优化过程第一步是初始化传声器位置,基于混沌序列生成包含随机传声器位置的初始种群,计算其对应的高频波束模式,代入式(14)中作为初始的目标波束模式,初始位置的选择不影响最终优化的结果。 图3 优化算法流程图 本文算法的特点是在全局搜索的遗传算法中穿插局部搜索算子模拟退火算法,且算法中加入logistics混沌序列,更好的为搜索方向提供指导。每次迭代会经过交叉-模拟退火-变异-模拟退火4步,且每一步中都会计算适应度值,且会将每次迭代中的最优结果记录作为下一次迭代中的指导,以确保迭代朝着寻找最小值的方向进行。算法的进程不断重复,直到达到最大迭代次数,在本文的优化过程中,将最大迭代次数设置为1 000。迭代完成后,获得最终阵列阵型所对应的波束模式最为接近目标波束模式,即波束宽度得到最大程度的减小,分辨率得到提高。 本文的优化分两步:第一步是基于渐开线多螺旋臂阵列设计,将设计中的几何参数、传声器数目、阵列孔径半径、旋臂数目和渐开螺旋线基圆半径作为优化的对象,先将其转换为传声器位置坐标,再作为输入量;第二步是将第一步中产生的传声器阵列坐标作为输入量,直接对坐标进行进一步的优化,提升分辨率。 优化的结果给出了在本文所提出阵列设计方案下最佳的参数组合:传声器数目为48,阵列孔径半径668 mm,旋臂数目4和渐开螺旋线基圆半径74 mm。在此几何参数组合下,各传声器位置如图4所示,将优化渐开线螺旋阵列中的各传声器坐标作为输入,将其优化成为一种随机阵列,该随机阵列阵型分布如图5所示,其中阵元数经过优化减少至23,减少了传声器的成本。为了显示优化阵列性能上的提升,将本文的两种优化阵列与几种不规则阵列进行对比研究。图6展示了用于对比研究的4种阵列阵型,分别为:Archimedean螺旋阵列,Arcondoulis螺旋阵列[15],Dougherty 多螺旋臂阵列和Underbrink多螺旋臂阵列。上述4种阵列均采用上述优化渐开线螺旋阵列中的最优几何参数组合来进行布置。 图4 优化渐开线螺旋阵列的传声器分布 图5 优化随机阵列的传声器分布 (a)Archimedean螺旋阵列 在对比研究中,首先应用各阵列进行点声源的二维映射,对映射结果进行对比分析。传声器阵列放置在z=0平面上,且采用二维网格进行映射。二维扫描网格平行于阵列所在平面,且网格间距为1/120的孔径大小,网格分布范围为:-1 所有的阵列的性能高低通过两个参数来进行衡量:频带内的波束宽度BW和动态范围DR值。150~2 000 Hz频带内的BW值,其中以50 Hz的频率分辨率计算38个单频窄带的波束宽度,如图7(a)所示;400 Hz以下频带的BW的数值变化如图7(b)所示。为了对比各阵列分辨率上的不同,分析随着频率增加,不同阵列间的BW值变化情况。本文优化的两个阵列,优化随机阵列相比于优化渐开线螺旋阵列在阵列分辨率上有明显的提高,在整个优化频带内前者都展现了更低的波束宽度BW,尤其400 Hz以下低频带内平均降低74 mm,最大降幅为200 Hz频率下122 mm。Arcondoulis螺旋阵列在整个优化频带内BW明显都高于其它阵列,在400 Hz以下更为明显,比优化随机阵列最大高出580 mm,平均高出310 mm。Dougherty多螺旋臂阵列在400 Hz以下时,BW比优化随机阵列最大高出316 mm,平均高出115 mm;在400 Hz以上,BW比优化随机阵列最大高出42 mm。Archimedean 螺旋阵列在400 Hz以下,BW最大高出优化随机阵列240 mm,在400 Hz以上最大高出66 mm。Underbrink多螺旋臂阵列在整个优化频带上与优化随机阵列在BW上几乎一致。 (a)BW对比结果 150~2 000 Hz频带内的DR值如图8(a)所示,400 Hz以下频带的DR值如图8(b)所示。DR值大小直接反映旁瓣的影响大小,DR值越大则旁瓣水平相对越低。优化随机阵列在400 Hz以上时,DR在10 dB附近波动并趋于稳定,最大达到13 dB。优化渐开线螺旋阵列在400 Hz以上时,DR主要保持在20~25 dB之间波动,这与Archimedean 螺旋阵列的DR在频带内的分布较为接近,但Archimedean螺旋阵列的DR波动更大。Arcondoulis螺旋阵列的DR值在400 Hz以上主要集中在20~30 dB范围内,其在600 Hz以上时DR范围基本优于其它阵列,最大可达30 dB。Dougherty多螺旋臂阵列和Underbrink多螺旋臂阵列在整个优化频带内DR变化趋势十分接近,但是Dougherty多螺旋臂阵列的DR值在400 Hz以上几乎全部大于Underbrink多螺旋臂阵列,平均高出4.24 dB。在400 Hz以下,所有阵列的DR都呈快速下降趋势,最终下降至5 dB以下,且各阵列的DR趋于接近。 (a)DR对比结果 为了研究在源深方向上分辨率的情况,将上述对比研究中的各阵列进行点声源的三维映射,从而验证本文提出的优化阵列在源深维度上分辨率性能。在本次仿真测试中,所有阵列均使用泛函波束成形算法对500 Hz和1 500 Hz两个频率的点声源进行映射。声源的映射本身采用三维网格,可以反映源深维度上的声场分布情况。三维扫描网格包括一个立体网格空间分布:-1 (a)优化渐开线螺旋阵列 (b)优化随机阵列 (c)Archimedean螺旋阵列 (a)优化渐开线螺旋阵列 (b)优化随机阵列 (c)Archimedean螺旋阵列 表1 频率500 Hz和1 500 Hz不同阵列BW值大小 本文利用基于改进遗传算法的优化过程,对渐开线多螺旋阵列几何参数和基于优化几何参数组合的传声器阵列阵元坐标进行优化,得到了令人满意的结果。通过优化得到的优化随机阵列中传声器数量仅为23个,传声器阵列的复杂性和实现成本得到降低。在所提出的优化随机阵列与其它参考阵列的对比中可看出:优化随机阵列展现出更小的波束宽度值和可接受的动态范围大小。除了关注二维声源定位,对三维声源定位时源深维度上的分辨率性能也进行对比分析,结果显示本文所提出的优化随机阵列在源深维度上的分辨率也得到有效提高。本文的关注点在于二三维声源辨识时低频分辨率不足的问题,优化过程在相对偏低的频带内进行,提出的优化随机阵列中的传声器数目相对已有的阵列形式偏少。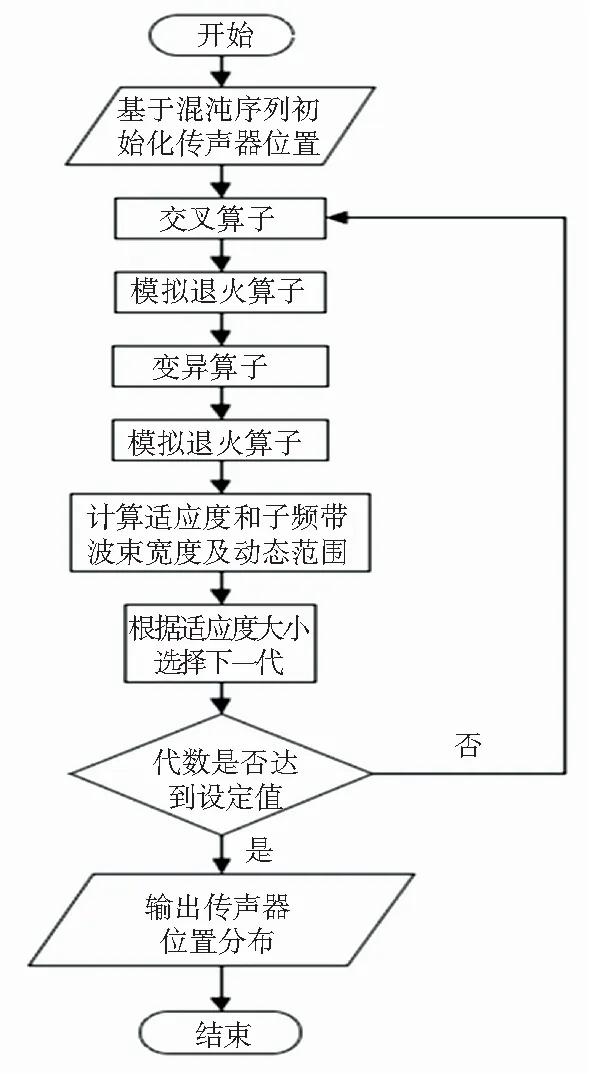
4 优化结果与分析
5 结束语
