近场相干声源三维定位MUSIC算法∗
2021-06-02邵元
邵元 杨 超 郭 辉
(上海工程技术大学机械与汽车工程学院 上海 201600)
1 引言
多重信号分类(MUSIC)算法是超分辨估计算法中的一种,常用于非相干远场信号的波达方向估计。但在近场环境中其精度大大降低将会导致算法失效。与此同时MUSIC算法也无法对相干声源的位置进行估计[1~5]。
MUSIC算法最初由Schmidt提出,随后有很多学者对MUSIC算法进行了研究和改进,其中远场环境下的二维MUSIC[6]算法被提出用来搜寻远场声源的方向。由于在近场环境下不同麦克风之间接收到的信号幅值具有差异,方向也不尽相同[7~8],文献[9]提出了基于均匀线性阵列的近场声源三维定位MUSIC算法。仿真表明该算法可准确地完成近场非相干声源位置估计。对于相干声源定位,比较常用的是空间平滑算法及其改进算法[10~12]。空间平滑算法综合性能较好,但在处理相干信号的过程中牺牲了有效阵列孔径。于是很多学者对其进行了改进,董玫在文献[13]里提出了修正的空间平滑算法。文献[14]提出了基于ES-MUSIC的空间平滑估计算法来解决远场相干信号位置估计问题。上述改进算法均有较好的分辨率,但被远场前提所限制导致无法在近场环境中使用。
为了解决近场相干声源位置估计问题,本文提出了近场相干声源三维定位MUSIC算法。本文算法在近场信号接收模型中结合空间平滑算法和修正MUSIC算法对接收信号做解相干处理,进而完成声源位置估计。仿真结果表明:本文算法可有效地解决相干信号协方差矩阵秩亏损的问题从而完成近场相干声源位置估计。
2 近场信号模型
根据声源与传声器阵列的距离,信号接收模型可分为近场模型和远场模型。近场的判断公式为

其中L为声源与传声器阵列的距离。K为阵列孔径,λ为信号波长。因为近场环境下不同麦克风接收信号的相位和幅值均有差异,声源位于近场时采用球面波模型要比传统远场平面波模型更加精确。
假设D个近场窄带信号辐射到由M个麦克风组成的阵列上,整个麦克风阵列的接收信号表达式为
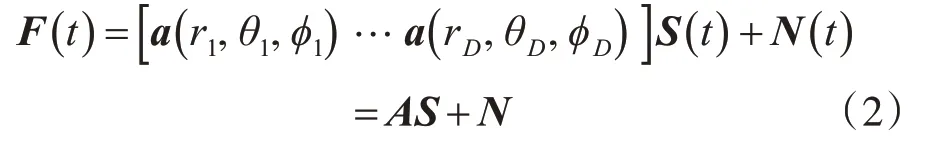
其中
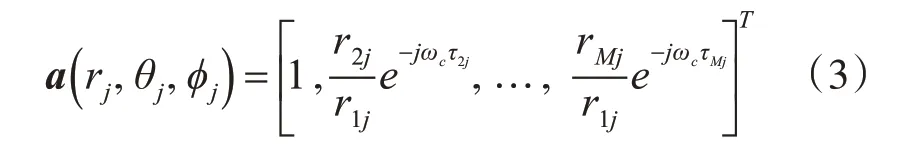
r代表声源和阵元的距离,ωc为声源的中心角频率,τij为第i个麦克风接收到第j个声源的相对时间延迟:
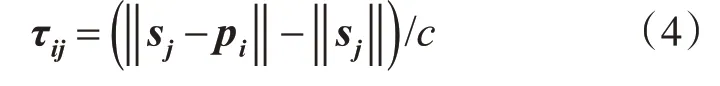
s1,s2,…sD为声源位置矢量,p1,p2,…p M为麦克风位置矢量,c为声波波速。
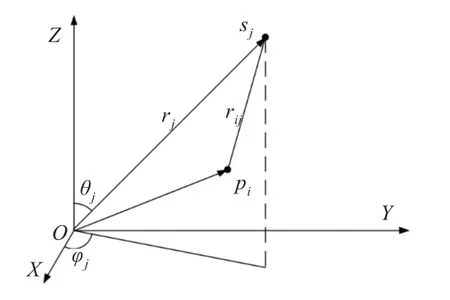
图1 麦克风阵列接收信号模型
3 近场相干声源三维定位算法
3.1 阵列预处理技术模型
信号相关无法保证噪声空间的特征向量与方向向量正交[15],所以需要对相干信号进行预处理。图2为空间平滑算法中的子阵列划分原理图。其中LX是总矩形阵列x方向的阵元个数,LY是总矩形阵列y方向的阵元个数。
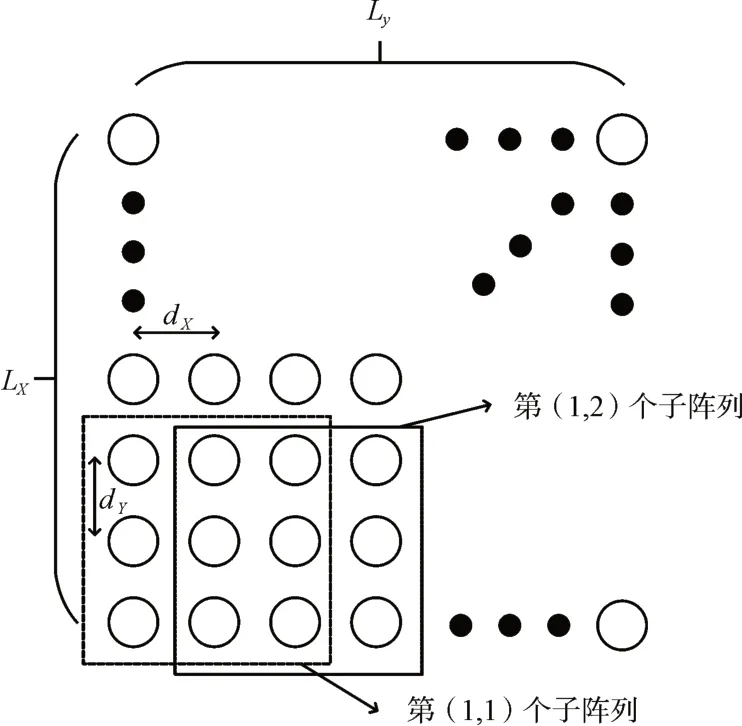
图2 子阵列划分原理图
子阵列的方向矩阵为

时间延迟τij为
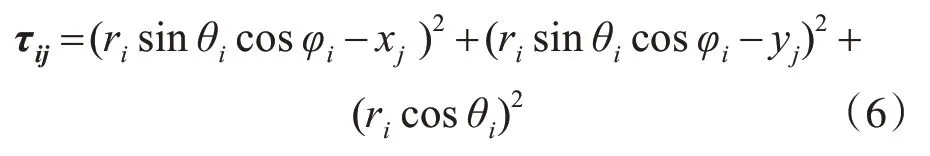
xj,yj是第j个阵元的横纵坐标。子阵列的信号接收模型为
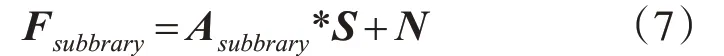
对F subbrary做协方差运算可得到R subbrary:

式(9)得到子阵的协方差矩阵的平均值R X

p为子阵列的个数。令

式中,F(t)*表示F(t)的复共轭矢量矩阵,J表示反向单位矩阵,那么对Y()t的求协方差矩阵为

将R X,R Y相加可得到R m:
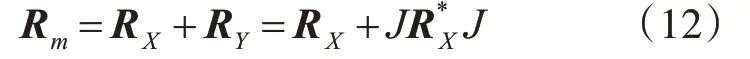
将R m代入三维MUSIC算法中即可完成相干信号的位置估计。
3.2 近场三维MUSIC算法
对式(12)进行特征分解并排序得到:
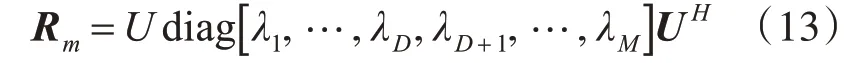
其中λ1,…,λD,λD+1,…,λM是特征值,U是对应的特征向量矩阵。根据特征值将U分解为两个空间,噪声和信号子空间,根据子空间理论定义空间谱函数为

使空间谱函数为极大值的θ,φ,r值即近场声源的俯仰角、方位角和距离。
4 仿真实验
4.1 仿真设计
本文算法的目的是对近场相干声源进行位置估计。首先在信噪比恒定(20dB)的情况下,对近场相干双声源进行定位。其次在不同信噪比下,进行以均方根误差为判断指标的误差分析。
仿真实验中采用3*3的均匀矩形阵列,阵列间距为15cm,在高斯白噪声背景下选择两个相干正弦信号(1800Hz)作为信号源。其他仿真参数设定见表1。
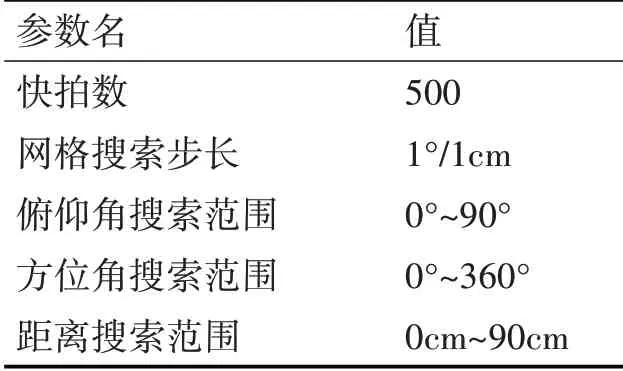
表1 本文算法参数
4.2 仿真分析
4.2.1 定位性能分析
图3是传统MUSIC算法对于两个近场相干声源的谱峰搜索结果图,因为相干信号协方差矩阵秩亏损的问题没有得到解决,传统MUSIC算法失效。图4为信噪比SNR=15dB的条件下两个相干声源的谱峰搜索结果图,其中尖锐谱峰所对应的横坐标即为算法估计出的声源位置参数。表2为实际声源位置与算法定位结果的数值对比。从表2和图4得到结论:本文算法可以对近场相干声源的位置进行准确估计。

图3 传统三维MUSIC的谱峰搜索图
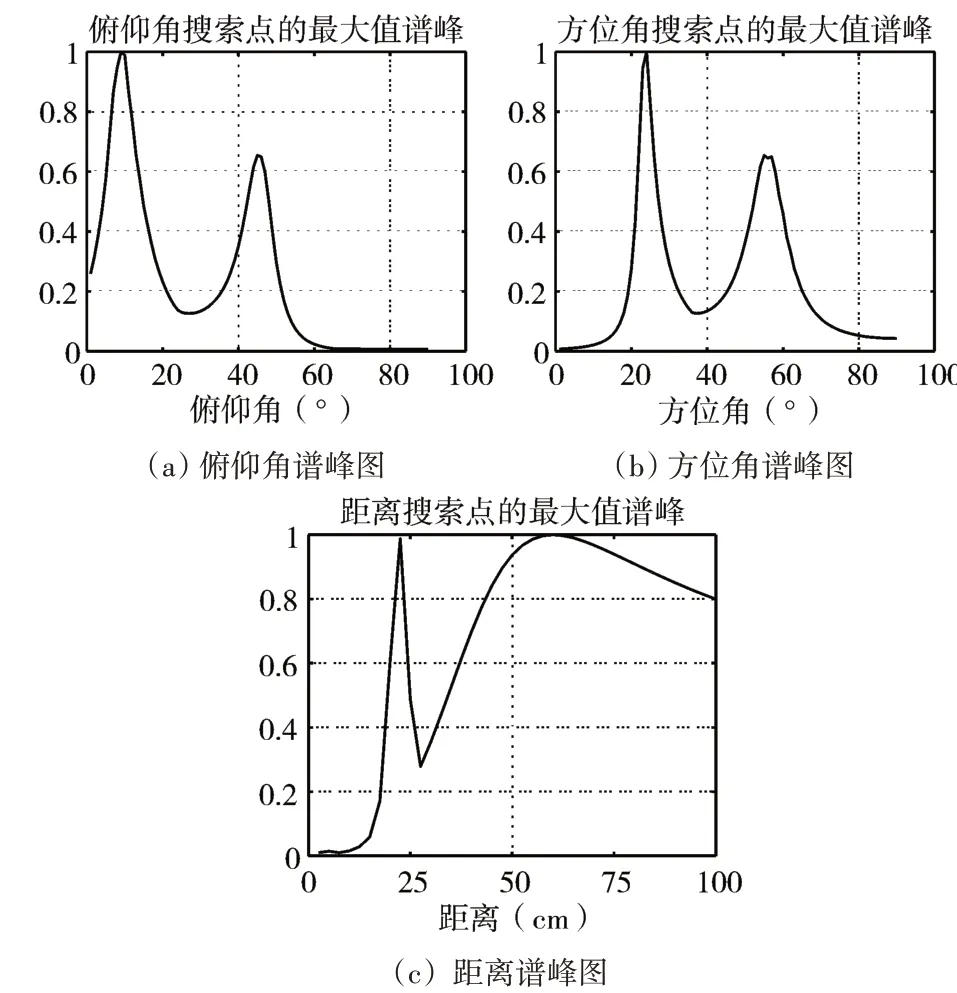
图4 本文算法的谱峰搜索图

表2 实际声源位置与算法定位结果对比
4.2.2 均方根误差分析
本节对极坐标系下近场声源的俯仰角,方位角和距离进行了定位误差分析。仿真下的相关参数设定见表1。图5为近场相干声源位置的俯仰角,方位角和距离随着SNR变化的均方根误差曲线。随着SNR增加,算法的均方根误差在减少,这说明随着SNR的增加,信号子空间和噪声子空间分离的更加彻底。本文算法可对近场相干声源的位置进行高精度估计。
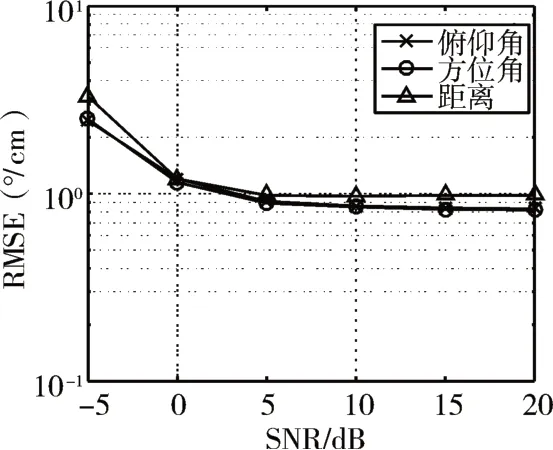
图5 均方根误差曲线
5 结语
针对传统MUSIC算法无法对近场相干声源进行位置估计的缺点,提出了一种近场相干声源三维定位MUSIC算法。本文算法结合了空间平滑算法和修正MUSIC算法对信号进行解相干处理。仿真表明本文算法可准确地对近场相干声源进行三维定位。
