长江经济带工业生态效率的时空差异及其影响因素研究

陈 杰， 王建民， 范玉环

(安徽理工大学 经济管理学院， 安徽 淮南 232000)

一、引言

长江经济带由横跨东中西三大区域的9省2市组成，是我国经济密度最高的经济地带之一,发展潜力巨大。长江经济带总面积约为205万平方公里，占全国的21.4%，2019年总人口约为6亿，占全国的43%，生产总值约为45.78万亿元，占同期全国总量的46.2%。然而在取得巨大经济发展成就的同时，其生态环境已不堪重负：长江中上游地区水土流失严重，石漠化灾害严重，中下游地区湖泊、湿地面积大量萎缩，高风险企业沿江密布，水生态安全问题突出，长三角地区大气污染排放负荷大，雾霾频发[1]。为切实保护和改善长江经济带生态环境，2017年国家相关部门发布了《长江经济带生态环境保护规划》,指出要将生态环境放在优先地位，一切经济活动都要以不破坏生态环境为前提；2018年4月，习近平在深入推动长江经济带发展座谈会上强调，必须从长远角度探索一条保护生态环境的绿色发展之路，体现国家政府对改善长江经济带生态环境的重视程度。在此背景下，本文基于长江经济带11省市的资源消耗、污染排放和工业总产值等相关数据，定量分析其工业生态效率，探索工业生态效率的外部影响因素，对长江经济带生态环境改善、实现区域可持续发展具有重要的理论与实践意义。

数据包络分析(DEA)模型因其所需指标较少、无需权重假设、避免人为主观影响等优点成为目前测算经济单元相对效率的主流方法[2]。随着国家生态文明建设进程的推进，学界也产生了许多高价值的研究结果，我国关于资源环境约束下的工业经济效率研究主要分为宏观和微观两个层面。其中宏观层面主要包括对省域、城市群等区域的工业生态效率的时序变化、空间相关性等方面进行研究[3]。如李成宇等采用BCC模型结合Malmquist指数对中国30省市的工业生态效率进行测算，并对其空间分布特征和影响因素进行了分析[4]；杨亦民、王梓龙利用基于非期望产出DEA模型对湖南省14个市州的工业绿色发展效率进行测算，选取6项工业生产指标进行影响因素分析，以期寻找改善工业生态效率的政策切入点[5]；张如波等利用网络DEA模型对长江三角洲35个城市工业生态系统及其经济、能源和环境子系统进行评价[6]；汪克亮、刘晓萌等等学者分别对山东省和安徽省的城市工业生态效率进行测度与评价[7-8]；田泽等对“一带一路”沿线省市区的工业生态效率的时空变化特征进行评价分析，并指出经济发展水平、城市结构等因素对工业生态效率有显著影响[9]。微观层面主要以工业企业生态效率的测算和影响因素研究为主。如王俊岭等结合钢铁行业特征建立基于DEA模型的生态效率评价指标体系，对2009—2016年我国钢铁工业的生态效率进行测算，并对其各年度的投入冗余进行了分析[10]；陈毅辉、苏凯利用传统BCC模型对福建工业企业生态效率进行测算，并结合空间计量模型对其进行影响因素分析[11]，但未考虑管理效率、环境影响等随机干扰的影响，难以探查效率低下的主要原因。Fried等学者基于此建立了三阶段DEA模型，目前在国内效率研究中被广泛采用。如张会恒、刘士栋利用三阶段DEA模型对我国工业各行业的生态效率进行测算分析，并指出外部环境等非经营性因素对提升生态效率非常明显[12]。

综上所述，无论是宏观或微观,对工业生态效率的研究都已有许多，但仍然存在不足，主要有以下两个方面：(1)工业生态效率与相关因素的作用机制复杂，相关文献从静态角度对工业生态效率的测度及评价较多，但对工业生态效率的动态演进及其机理探索不足；(2)在模型选择上，大多采用传统DEA和SBM模型，前者未考虑松弛变量的影响，测算值存在偏差，且二者都无法对效率值为1的有效决策单元进行进一步评价和排序。本文采用Super-SBM模型结合Malmquist指数法从静态和动态两个角度对长江经济带工业生态效率的时空演变和区域差异进行分析，并借助Tobit回归模型研究其外部影响因素，以期为促进我国区域工业绿色可持续发展提供理论依据和现实参考。

二、研究方法

(一)Super-SBM模型

DEA即数据包络分析，由美国著名运筹学家Charnes和Cooper于1978年提出[13]，是一种运用数学线性规划方法评价经济系统生产前沿面有效性的非参数方法。DEA的传统模型包括CCR模型和BCC模型，两者虽然很好地克服了参数估计法系统误差大的问题，但未考虑投入与产出的松弛变量的影响，进而导致效率值偏差。基于此，Tone于2001年提出利用松弛变量测度效率的非径向SBM模型(Slacks-based Measure)[14]，并在SBM的基础上完善，于2002年提出以修正松弛变量为基础的Super-SBM模型，较好地解决了传统DEA模型和SBM模型无法对有效单元进行进一步评价和排序的问题。本文将采用Super-SBM模型对长江经济带各省市的工业生态效率进行静态分析。Super-SBM模型表达式如(1)所示。

(1)

其中ρ为效率值，m、s分别表示投入与产出数量，xi、yr表示投入与产出要素，λ为权重向量。

(二)Malmquist指数模型

Malmquist指数最早由Malmquist于1953年提出，后由RolfFäre等人将这方法与DEA理论相结合，使得Malmquist指数模型广泛应用。Malmquist指数法将全要素生产率变动指数(TFPC)分解为技术变化指数(TC)和技术效率变化指数(EC)，即TFPC=TC×EC，其表达式如(2)所示。

M0(xt,yt,xt+1,yt+1)=

(2)

其中技术效率变化指数(EC)可进一步分解为纯技术效率变化指数(PEC)和规模效率变化指数(SEC)，进而全要素生产率变动指数可表示为TFPC=TC×EC=TC×PEC×SEC,其表达式如(3)所示。

(3)

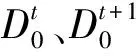
(三)Tobit回归模型

本文通过建立回归模型来进一步探究长江经济带工业生态效率的影响因素，选取超效率SBM模型测出的效率值为被解释变量，外部具有代表性的因素作为解释变量，以此探究各外部因素对长江经济带工业生态效率的影响。由于超效率SBM测算出的效率值属于截断离散数据，若采用最小二乘法进行回归分析，可能会出现参数估计量的偏误和不一致现象，因此本文采用Tobit模型，该模型最早由Tobin提出，后由Coelli等人改进提出“两阶段法”，可以用于解决截断或受限因变量建模问题，具体形式如下：

其中，Yi、Xi分别为截断因变量和自变量，β为待估参数，εi为随机误差项。

三、实证分析

(一)指标体系建立与数据来源

在对长江经济带各省市进行工业生态效率评价时，投入与产出指标选取的准确性对结果效率值影响很大。因此本文结合工业生态效率特点，参考相关文献[4-8]，同时考虑数据的科学性、可得性等因素构建评价指标体系。具体评价指标体系如表1所示。

表1 长江经济带工业生态效率评价指标体系

本文研究对象为长江经济带11个省市2010—2017年间的工业生态效率，实证分析的所有数据均来自于历年《中国统计年鉴》[15]和各省市历年统计年鉴。变量描述统计特征如表2所示。

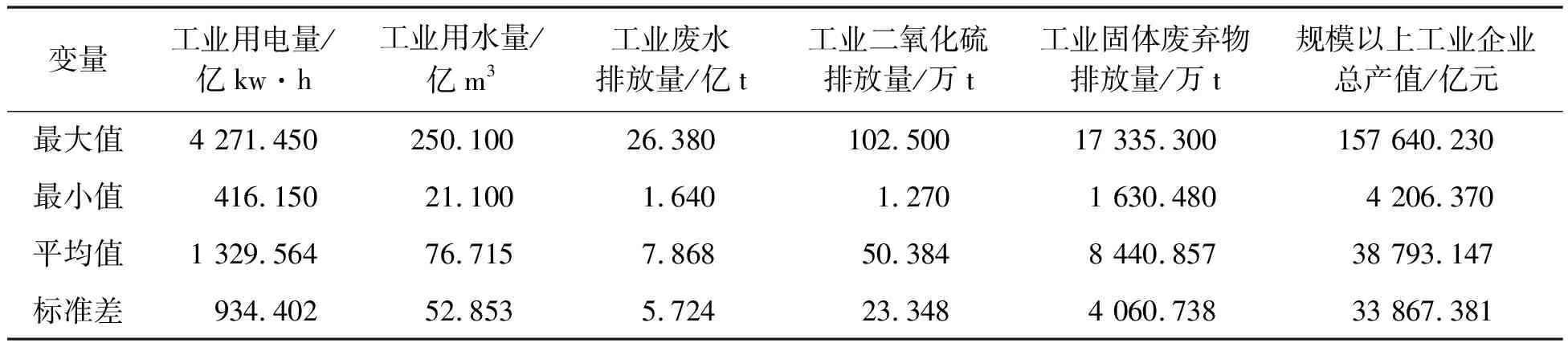
表2 样本投入产出变量描述统计特征

(二)工业生态效率静态分析

本文采用Super-SBM模型，利用DEA-Solver Pro.5.0软件从静态的角度测算了长江经济带2010—2017年11个省市的工业生态效率值，具体结果如表3所示。汪克亮[16]等学者将长江经济带划分为三大区域，其中上游区域包括云南、贵州、四川、重庆；中游区域包括湖南、湖北、江西、安徽；下游区域包括江苏、浙江、上海。上中下游区域工业生态效率的趋势图如图1所示。

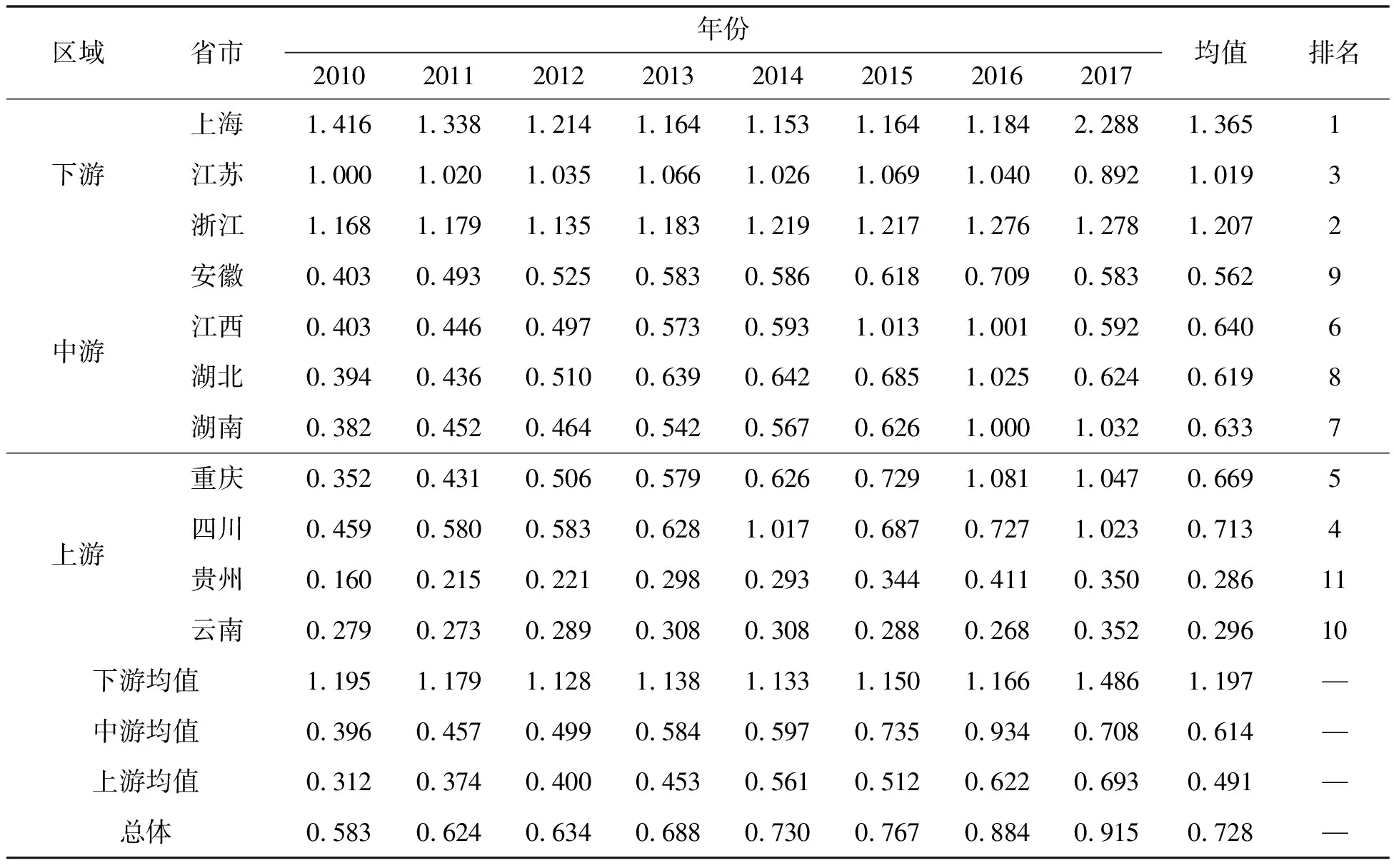
表3 2010—2017年长江经济带各省市工业生态效率测算值

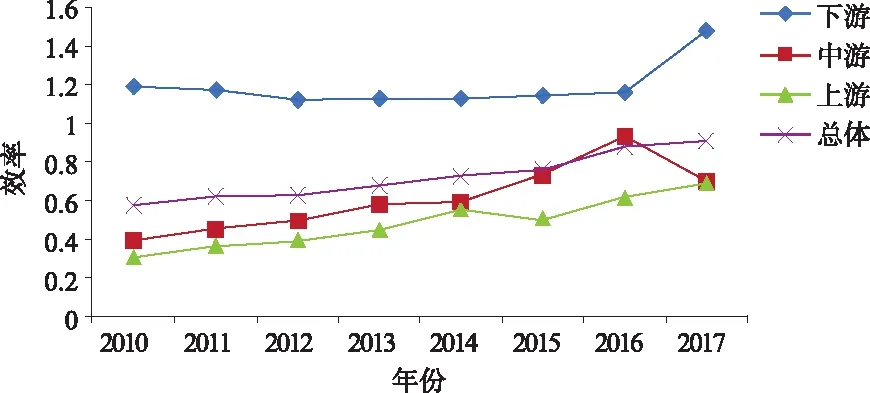
图1 2010—2017年长江经济带上中下游工业生态效率变化图

以整体的视角来看，2010—2017年研究期间长江经济带工业生态效率呈现逐年递增的趋势，整体平均值由2010年0.583上升至2017年0.915，虽然每年的提升幅度不同，但仍然说明研究期间长江经济带工业生态效率发展态势良好且稳定。研究期间整体效率平均值为0.728，由此可见其整体的工业生态效率水平不高，仍有较大的改善空间。

从区域的角度来看，长江经济带工业生态效率水平下游>中游>上游。下游最高，研究期间均值为1.197，大于1，属于DEA有效区，其次是中游区域，均值为0.614，最低是上区域，均值仅为0.491。由图1可以直观地看出三大区域之间的显著差异，下游区域工业生态效率平均值远高于其他区域和总体均值，而中上游区域则基本上处于总体均值以下。造成这一现象的原因是下游地区地理位置优越，经济发展好，对生态环境的重视程度高；上游区域经济水平较低，但是自然资源丰富，为了追求经济的发展而引入许多高污染企业，导致在资源开发过程中对生态环境造成破坏；而中游地区相较上下游，在经济发展和自然资源方面都处于中等水平，因此其工业生态效率介于二者之间。值得一提的是虽然中上游工业生态效率较低，但上升趋势正逐渐靠近总体平均水平，说明中上游区域的工业生态体系正在逐渐改善。

从各省市独立的视角来看，2010—2017年研究期间工业生态效率平均值大于1的省市排名分别为上海(1.365)、浙江(1.207)、江苏(1.019)，这三个省市处于生态技术前沿面上，是其他省市追赶的对象。说明此三省市在推动工业经济发展的过程中注重能源合理配置与生态环境保护，其主要原因是苏浙沪地区地理交通位置优越，是资本、人才、产业等经济要素的高度聚集地，工业技术和管理水平都处于全国领先水平，政府资源利用率和环境保护重视程度都较高；其次四川省是效率值最接近1的省市，效率值为0.713，仍有30%的改善空间，四川省在研究期间效率值出现骤增与骤降：首先由2013年0.628跳跃至2014年1.017，2015年又回弹至0.687，而后稳步提高至2017年1.023。主要原因是四川省环境保护厅和财政厅2014年联合发布了多项生态环境保护政策，采用“以奖代补”的方式，促进各高污染企业进行污染总量减排和环境治理，在2015—2017年间产生了显著成效；效率均值排名倒数的两个省市是云南和贵州，效率均值仅为0.296和0.286，不足效率值第一的上海市的1/4，具有非常大的提升空间，这与其地理资源环境丰富、经济发展速度缓慢和粗放型生产方式是分不开的，但是其发展态势良好：云南省在研究期间由0.279提高至0.352，贵州省由0.160提高到0.350，说明两省正在积极地改变经济发展模式，提高生态效率；其余5省市包括重庆(0.669)、江西(0.640)、湖南(0.633)、湖北(0.619)、安徽(0.562)，各省市效率值相差不大，皆在0.50-0.70范围不等。

(三)工业生态效率动态分析

上文从静态视角对长江经济带的工业生态效率进行了分析，为进一步探究工业生态效率随时间的动态变化以及变化的内在结构性原因，利用DEAP2.1测算长江经济带的Malmquist指数及其分解值，测算结果如表4、表5所示。

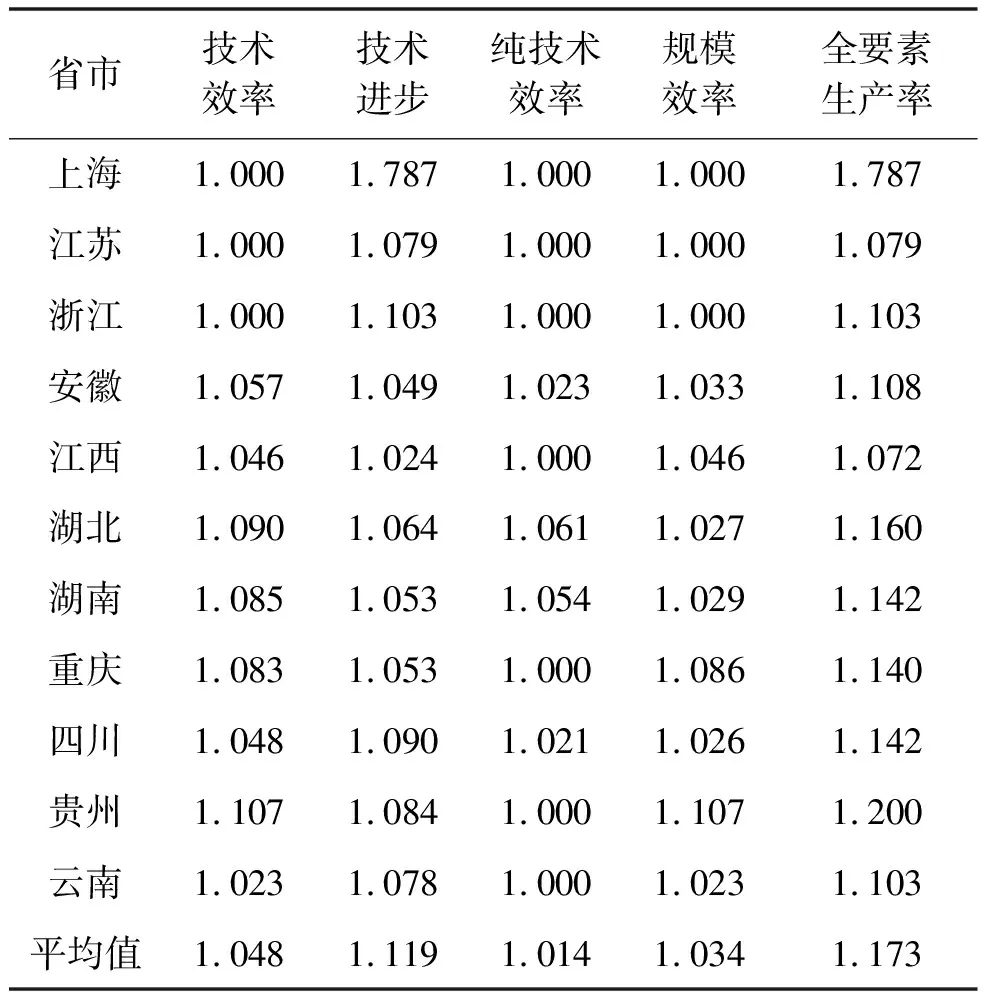
表4 2010—2017年长江经济带工业生态效率Malmquist指数及其分解

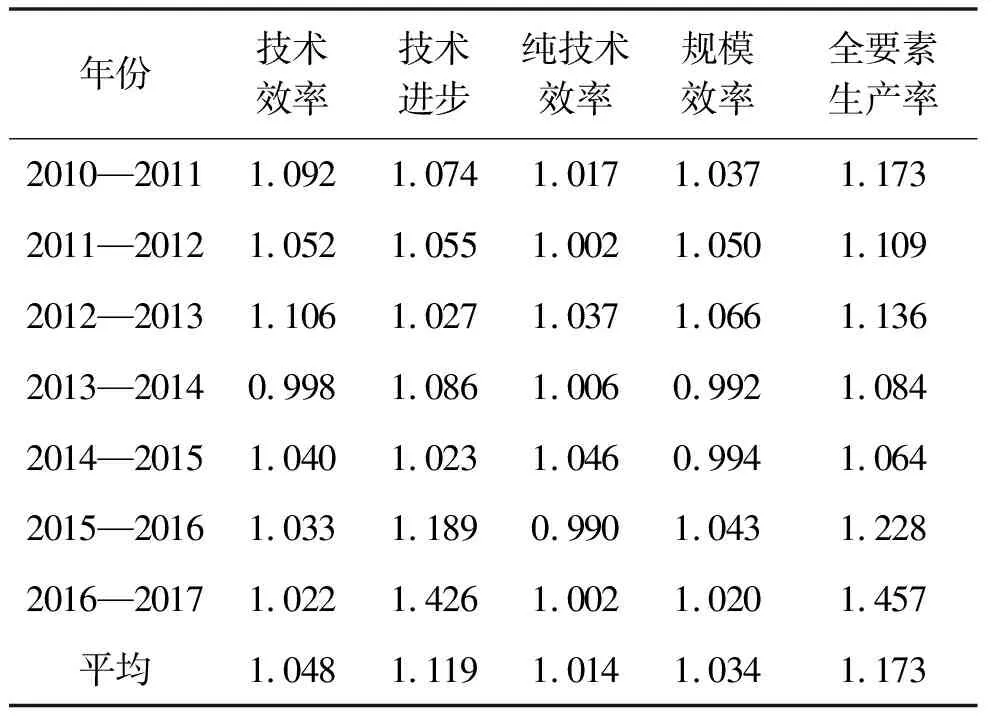
表5 长江经济带各年份平均全要素生产率及其分解

由表4测量结果可知，整体来看，在研究期间，长江经济带工业生态效率全要素生产率平均值为1.173，大于1，表明长江经济带整体的的工业生态效率在研究期间呈上升态势，增长幅度为17.3%，其中技术进步是主要推动力，年均增长11.9%，技术进步增速最快的是上海，高达78.7%。其次是技术效率，年均增长4.8%，研究期间纯技术效率和规模效率也分别小幅度增长1.4%和3.4%，其中多地的纯技术效率为停滞状态，导致纯技术效率对全要素生产率贡献最低。从省市的角度来看，11个省市中全要素生产率最高的是上海市，为1.787，远高于其他省市，也正是其拉高了整体的平均水平，若除去上海市其他10省市的全要素生产率平均值仅为1.108。全要素生产率最低的则是江西省，研究期间年均增幅仅为7.2%，两者差距悬殊。特别需要说明的是，上海、江苏、浙江三省全要素生产率的提高仅由技术进步拉动，改善路径过于单一，若采取措施对其规模效率和技术效率进行改善，其全要素生产率将会进一步提高。

从表5可以看出，在研究期间长江经济带各年度工业生态全要素生产率均大于1，说明长江经济带工业生态效率体系逐年完善，这得益于国家近年来对生态效率的重视。从各年份来看，2010-2011年全要素生产率为1.173，较上一年涨幅为17.3%，各项分解指标均有不同程度的提升，但主要依赖于技术效率(9.2%)和技术进步(7.4%)的提升。2011—2012年长江经济带工业生态效率全要素生产率为1.109，除去纯技术效率仅增长0.2%之外，技术效率(5.2%)、技术进步(5.5%)和规模效率(5.0%)都促进了工业生态效率的提高。2012—2013年比上一年增长了13.6%，由其分解指标可知，主要是由于技术效率(10.6%)和规模效率(6.6%)的提高。2013—2014年全要素生产效率增长8.4%，由其分解指标可知主要是由技术进步带来的提升。2014—2015年全要素生产率为1.064，是研究期间增幅最低的一年，主要原因是技术进步的增长速度放缓和规模效率的下降。2015—2016年全要素生产率增长22.8%，技术进步较上一年增长了18.9%，说明在此期间技术进步是推动工业生态效率提升的主要原因。2016—2017年全要素生产率为1.457，是研究期间涨幅最快的一年，达到45.7%，其中该阶段技术进步贡献最大，较上一年增长42.6%。综上所述，在研究期间全要素生产率每年都实现稳定增长，但每年推动增长的要素各不相同，其中技术进步占比最大，最高增长达42.6%，而技术效率、纯技术效率和规模效率每年贡献不大，或偶有下降。因此长江经济带在改善工业生态效率时要注重提高其工业技术和企业管理水平，改善其规模效率。

(四)工业生态效率影响因素分析

通过前文对长江经济带工业生态效率静态与动态的分析，发现长江经济带上中下游11个省市工业生态效率异质性特征显著。为探讨其原因，本文采用Tobit回归模型对其进行影响因素分析。影响工业生态效率的因素有许多，参考已有研究成果[4,5,6,9,16,17]，并结合长江经济带的区域特点，本文选取经济发展水平、研发强度等五个方面的影响因素，各因素的定义以及预期影响如表6所示。

表6 各影响因素的定义及预期影响

本文构建的回归模型具体如下：

IEEi=β0+β1lnGDPit+β2INDUSit+β3ERit+β4FDIit+β5RDIi+εit

其中IEEi是各省市以及上中下游地区的工业生态效率值，β0、β1～β5为待估参数，εit为随机干扰项。利用Stata12.0软件，得出Tobit模型的回归结果如表7所示。

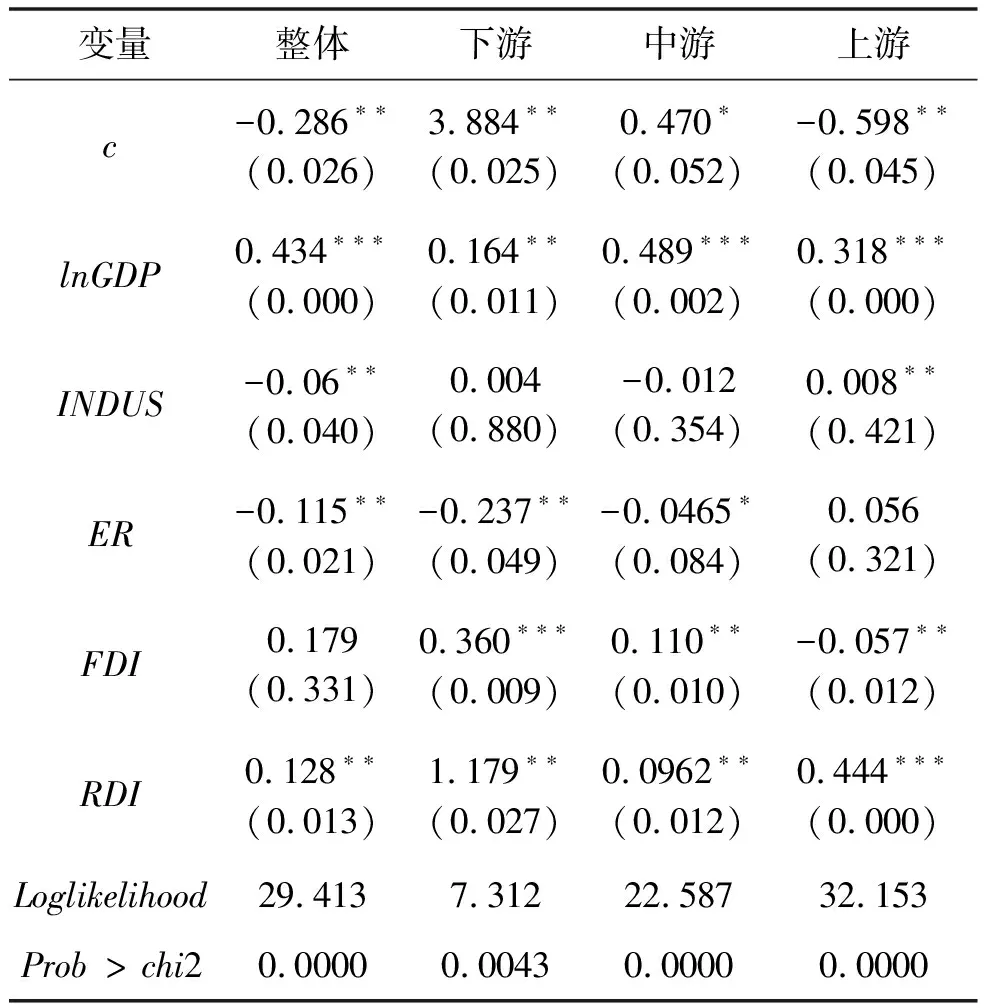
表7 长江经济带工业生态效率Tobit模型回归结果

由表7的Tobit回归结果可知：各模型的Prob>chi2结果均小于0.01，可知各模型的拟合度较好。以下就长江经济带工业生态效率影响因素进行分析。

1.由结果可知，人均生产总值对长江经济带整体和其上中下游区域都有不同程度的促进作用，且回归方程的系数皆在5%的显著性水平下通过检验，这说明地区经济水平的提高对地区工业生态效率有较好的改善作用。好的经济水平对资金、人才、技术等要素都有较强的吸引作用，这些要素对地区工业生态效率的改善提供了强有力的支持。

2.产业结构对长江经济带整体工业生态效率有抑制作用，但程度较小，回归系数为-0.06，通过5%的显著性水平检验，但是产业结构对区域工业生态效率的影响皆不显著。由生态效率的定义可知，对长江经济带而言，第二产业发展对工业的经济增长小于其对环境造成的负面影响。

3.环境治理与长江经济带整体工业生态效率呈现负相关，与预期结果相反。中下游的回归结果也类似，只对上游有促进作用，但未通过显著性水平检验。说明加大环境治理力度并不能有效地改进长江经济带工业生态效率。

4.外资利用水平对整体的工业生态效率影响不显著，对区域工业生态效率影响有正有负。对中下游区域有显著的推动作用，对上游地区有明显的抑制作用。究其原因，上游地区为实现经济的崛起，只关注外资数量而忽视了质量，导致众多高污染企业入驻，虽然对经济发展有促进作用，却是以牺牲生态环境为代价。

5.研发强度与长江经济带工业生态效率显著正相关，在5%的显著性水平上通过检验，对效率值的影响程度仅次于经济发展，研发强度每提高一个百分点能对工业生态效率值改善12.8%，而且对各区域也有不同程度的促进作用。提高研发投入能够促进工业企业进行技术、设备和管理方法的更新改善，使之能够以更小的资源环境代价创造更大的经济效益。

四、结论与建议

(一)结论

本文对长江经济带2010—2017年工业生态效率及其动态变化进行研究，并对长江经济带工业生态效率外部影响因素进行回归分析，得出以下结论。

其一，在研究期间，长江经济带各年度工业生态效率值普遍较低，但发展态势良好，逐年上升，从2010—2017年效率值提高了近60%。区域差距显著，呈现下游>整体>中游>上游，且下游效率值远高于中上游。省际差距显著，排名最高与最低工业生态效率值相差近1.1，排名前三的苏浙沪地区研究期间一直保持大于1的状态，是其他省份赶超的目标。

其二，研究期间各省市工业生态效率增长速度差距显著，最快与最慢相差70%，各省市的全要素生产率分解指标中技术进步对长江经济带工业生态效率贡献最大。从时间角度来看，研究期间各年度全要素生产率均大于1，增长幅度有高有低，技术进步均为正，且增长率水平较高，是全要素生产率的主要推动力。

其三，经济发展和研发强度对长江经济带整体以及上中下游区域的工业生态效率均有显著的促进作用，说明经济水平和研发投入的提高都能对长江经济带工业生态效率有显著的改善。产业结构对整体有轻微的抑制作用，环境治理与整体及中下游的工业生态效率呈现不同程度的负相关，表明加强环境治理并不能有效提高工业生态效率。外资利用水平对上中下游的影响较为复杂，由于上中下游经济环境、资源条件等情况不同，其对工业生态效率影响有正有负。

(二)建议

要打破长江经济带区域限制，实现区域联合发展，引导下游先进的技术和管理经验向中上游转移，提高长江经济带整体的经济发展质量。实施创新驱动发展，加大科研投入，引进高端技术人才，提高工业企业的自主创新能力，使技术创新成为长江经济带绿色发展的新推动力。优化产业结构，中上游区域省市应因地制宜，调整能源结构和工业结构，淘汰落后产能，加快长江经济带发展动力向第三产业转移的步伐。加强外资引进门槛，特别是中上游地区在引进外资时要统筹经济发展与生态环境，避免成为发达国家高污染企业的“避难所”。