自适应粒子群优化的HMM故障诊断方法及应用
2021-11-10王大为张绍伟张学成
郭 森,王大为,张绍伟,张学成
(1.上海机电工程研究所,上海 201109;2.陆军装备部驻上海地区第三军代室,上海 201109)
伴随着机器学习等人工智能技术的飞速发展,智能化技术在军事装备中的应用也在不断深入[1]。隐马尔科夫模型(hidden Markov model,HMM)自20世纪70年代末由Baum创建以来[2],因其强大的识别能力在语音识别领域取得了巨大成功[3],并逐渐在图像处理、设备状态识别、故障诊断等模式识别方面应用[4-7]。但是,将HMM应用于装备的故障诊断过程当中出现了一些不足,主要是由于该模型用于解决学习问题的Baum-Welch算法在参数寻优时会出现收敛到局部极值的情况,从而导致模型诊断结果精度不够[8-9]。
针对这一问题,许多学者引入群体智能优化算法来对HMM模型参数训练过程进行优化,提高学习效率及精度。文献[8]将粒子群算法(PSO)引入HMM的参数优化过程,实现全局优化的目的,并将改进后的模型应用到对报警信息识别和预测中;文献[10]将鸟群算法(BSA)与Baum-Welch算法相结合,可以有效跳出局部极值点,相对传统的HMM训练算法能够取得更好的训练结果;文献[11]提出一种带极值扰动的自适应粒子群算法,将改进后的粒子群算法引入到HMM的训练中,对其初始参数进行了优化,结果表明改进后的HMM具有较高的识别能力。
本文提出一种基于自适应粒子群算法优化的HMM方法,在PSO算法中增加惯性权重因子,通过动态控制惯性权重因子及加速因子的大小,改进PSO算法的全局搜索能力,提高寻优效率。并且,利用改进的PSO算法对HMM参数学习过程进行优化。将其应用到油机电站的故障诊断当中,与传统方法相比,诊断的效率和精度得到了有效地提升。
1 粒子群算法及其改进
1.1 PSO算法基本原理
PSO算法是一种用于非线性函数优化的集群智能优化算法[12],它在解决大规模非线性问题中具有更高的优化效率和更好的优化结果。该算法将各个备选解称为“粒子”,全部的粒子集合称作“种群”。PSO算法首先生成初始种群,即在可行解空间当中随机初始化生成一群粒子,并根据要优化的目标函数确定与之相对应的适应度值。优化过程就是初始种群在可行解空间内部飞行,并寻找最大或最小适应度值的过程,粒子飞行的方向与距离由速度决定。
其数学过程描述如下:
设搜索空间维数为D,总粒子数为N,第i个粒子的位置表示为向量xi=(xi1,xi2,…,xiD),第i个粒子当前搜索到的最优位置为pbesti=(Pi1,Pi2,…,PiD),整个粒子群当前搜索到的最优位置为gbest=(g1,g2,…,gD),第i个粒子的位置变化率(即速度)为向量vi=(vi1,vi2,…,viD),则粒子i的d维速度和位置可按照式(1)、(2)进行迭代更新:
vid(t+1)=vid(t)+c1r1(pid(t)-xid(t))+
c2r2(gd(t)-xid(t))
(1)
xid(t+1)=xid(t)+vid(t+1),1≤i≤N,1≤d≤D
(2)
式中:c1、c2为正数,称作加速因子。c1调节粒子飞向自身最好位置方向上的步长;c2调节粒子飞向全局最好位置方向上的步长。r1、r2为[0,1]的随机数。
通过比较更新前后各粒子的适应度值,对单个粒子最优位置及全局最优位置进行更新,直到满足迭代终止条件。
1.2 PSO算法的自适应改进
与其它群体智能算法相比,PSO算法概念简单,易于编程实现求解,但在优化过程中同样会面临易于陷入局部极值点、搜索精度不高、收敛速度慢的问题。为此引入惯性权重因子ω,对粒子飞行速度进行调节,提高PSO算法的收敛速度及全局搜索能力,使其能够快速得到全局最优结果[13]。惯性权重因子ω对速度的调节原理如式(3)所示:
vid(t+1)=ωvid(t)+c1r1(pid(t)-xid(t))+
c2r2(gd(t)-xid(t))
(3)
由式(3)可以看出,引入的ω代表的含义主要对上一代粒子状态对当前粒子状态的影响程度,ω取值越大,则上一代粒子状态对与当前粒子的状态影响越大;反之,影响则越小。同时,算法的全局搜索能力也会随着ω的增大而提高。因此,通过控制惯性权重因子ω的大小,可以改进粒子群算法的全局搜索能力,当ω值取为常数1时,式(3)即退化为基本粒子群算法的速度更新公式。
为了进一步提高粒子群算法的优化性能,提升算法效率,采用基于距离控制因子的自适应调整策略来动态修正惯性权重ω及加速因子c1、c2,原理如式(4)所示:
(4)
式中:disti表示各粒子到全局最优值的平均距离;max(dist)表示至今平均距离的最大值;cont表示距离控制因子,即各粒子到全局最优点的平均距离与平均距离最大值的比值。
2 隐马尔科夫模型及其优化
2.1 隐马尔科夫模型
HMM类似于一阶Markov过程,不同点是HMM是一个双内嵌式随机过程,即HMM是由两个随机过程组成,一个是状态转移序列,它对应着一个单纯Markov过程;另一个是每次转移时输出的符号组成的符号序列。其中,状态转移随机过程是不可观测的,只能通过另一个随机过程的输出观察序列观测。
HMM可以通过5个参数来进行定量描述:
(1)系统状态空间Qt∈(q1,q2,…,qN),其中N为状态数目;
(2)观测值序列Ot∈(o1,o2,…,oM),其中M为系统观测值数目;
(3)系统初始状态概率分布π=(π1,π2,…,πN);
(4)系统状态转移矩阵A={aij}N×N,其中aij=P(Qt+1=qj|Qt=qi),1≤i,j≤N;
(5)观测值转移概率矩阵B={bjk}N×M,其中bjk=P(Ot=Vk|Qt=qj),1≤j≤N,1≤k≤M。
通常HMM模型记为λ=(N,M,π,A,B),简记为λ=(π,A,B)。一部分随机过程由参数π和A表示,另一部分用参数B来表示。
在实际工程应用当中,HMM主要解决三个问题:评估问题、解码问题和学习问题。评估问题主要解是在模型λ和观测序列O已知的条件下,计算在此模型下产生该观测序列的概率P(O|λ),可以利用Forward-Backward算法进行求解;解码问题主要是在模型λ和观测序列O已知的条件下,确定此模型下产生相应观测序列的最优状态序列Q,可以利用Viterbi算法加以解决;学习问题即HMM模型的参数寻优,通过对多个观测序列O进行学习,对HMM模型参数λ=(π,A,B)进行调整使得P(O|λ)最大,可以利用Baum-Welch算法进行训练。
解决HMM参数学习问题的Baum-Welch算法是通过迭代逐步逼近极大化似然函数的下界实现的,它只能保证收敛到对数似然函数序列的局部极值点,而非全局极值点。在HMM理论中,通过训练数据集对HMM参数进行训练时,不同的初始模型参数对训练结果有较大影响,在初始模型参数适当时才能求得与全局最优值接近的局部极大值。较其他参数而言,观测值概率矩阵的初始值对训练结果有较大影响[14-15],故使用优化算法对其初值选取进行优化。
2.2 基于自适应PSO的初始参数优化
利用改进的PSO算法对隐马尔科夫模型初始参数优化的流程如图1所示。优化过程中,每一个粒子代表一个初始参数即观测值转移概率矩阵B,选择Forward-Backward算法作为适应度函数,计算每个粒子的输出似然概率值P(O|λ)作为粒子适应度值,并据此来选择更优的个体粒子,选取的原则为:适应度值越大的粒子位置越优。利用Forward-Backward算法计算P(O|λ)原理如式(5)所示:

图1 HMM初始参数优化流程Fig.1 Flowchart of optimization for HMM initial parameter
(5)
式中:T为观测序列时间长度;αt(i)通过前向算法迭代计算;βt(i)通过后向算法迭代计算。
通过对比每次迭代后各粒子的适应度值来对粒子群个体最优位置pbest和全局最优位置gbest进行更新,粒子的速度按式(3)进行自适应更新,根据粒子速度来更新整个粒子群,反复迭代直至满足终止条件,得到最优的初始观测值转移概率矩阵。
3 基于自适应PSO-HMM故障诊断方法
在改进粒子群优化算法的基础上,本文提出一种基于自适应PSO-HMM的故障诊断方法,故障诊断流程如图2所示。故障诊断主要分为两个方面,一方面是不同故障状态下HMM模型的建立,另一方面是利用建立的不同故障模型对待诊断数据进行处理,得到诊断结果。
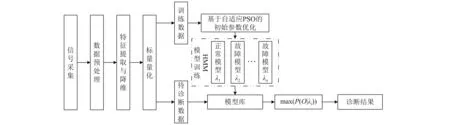
图2 基于自适应PSO-HMM的故障诊断流程Fig.2 Flowchart of fault diagnosis based on adaptive PSO-HMM
3.1 数据预处理
油机电站故障诊断的数据来源于不同状态下的振动信号,油机振动时产生的噪声对有用信号有所掩盖。因此,在提取特征之前需要对柴油机故障振动信号进行有效的降噪处理。
而且由于油机电站故障发生时,常常会伴随着短时脉冲、间断等突发性异常信号的出现,基于小波分解等常用的信号降噪方法在处理这些异常信号时,计算复杂,费时费力。研究表明,在分析突发性故障信号时,数学形态滤波法更有优势[16]。因此,采用多尺度形态滤波器对油机电站的振动数据进行去噪预处理。
3.2 特征提取与降维量化
油机运行过程中的振动信号含有多形式、多特征、多征兆信息,这些信息蕴含在多个特征空间内,而所采集的振动信号只是一维的时域信息。为了全面反映油机的特征,从多个特征域提取设备的振动特征,主要包括时域范围内的均值、方差、均方根值、波形指标、峰值指标、脉冲指标、裕度指标、峭度指标、歪度指标等,频域范围内的频率、幅值等,时频域的小波包能量谱等,总共37维特征。
故障特征集构造完毕之后,为提升算法效率,引入核主元分析(KPCA)方法对其进行维数约简,融合多个复杂性能指标,删除冗余,保留反应故障状态的主要特征,减少模型训练时间。将筛选后的故障特征集进行归一化处理并量化,完成HMM模型训练之前的数据准备工作。
3.3 HMM模型训练
HMM模型训练过程主要有两部分,一是利用自适应PSO算法对模型初始参数进行优化,二是根据参数初始化结果采用Baum-Welch算法对模型参数进行寻优,得到油机电站不同状态的HMM模型。
3.4 故障诊断
完成油机电站各状态下HMM模型的建立之后,即可以针对实测数据进行诊断,根据模型的输出结果来判断油机的故障类型。
根据图2故障诊断流程,待诊断油机振动数据也需要进行预处理进行去噪,之后提取故障特征并降维量化处理,形成待诊断数据集。将经降维量化之后的特征集输入至经过训练的各状态HMM模型,采用Forward-Backward算法计算各模型输出结果即对数似然概率值,选择似然概率值较大的模型对应油机待诊断数据所属的故障模式,完成故障诊断。
4 仿真验证
4.1 振动特征提取
本文采用油机电站实际振动数据对上述自适应PSO-HMM故障诊断方法进行仿真,试验选用康明斯EQB190-20型号油机,在空载情况下设置正常、供气不足、进气门间隙异常三种状态,采用加速度传感器采集油机缸盖振动信号,采样频率设置为20.48 kHz,采集的数据包括三种状态下各500组振动数据。在此基础上分析自适应PSO算法优化性能及优化之后HMM故障诊断的精度。仿真试验平台采用i5-8500处理器,内存8 GB,操作系统为64位Windows 7系统。
首先对各组数据先进行高通滤波,然后采用多尺度数学形态滤波方法进行去噪,结果示例如图3。提取混合域振动特征,并使用KPCA方法对混合域特征进行降维和归一化处理,其3维特征累积贡献率即达到90%以上,如图4所示,三种状态基本能够分离。将主元累积贡献率设置为96%时,混合域特征维度降低为7维,继续增加维度,累积贡献率并无明显提高。因此,选择此7维特征作为融合后的故障样本进行量化处理,随机选取各状态400组样本作为训练数据用于HMM模型训练,剩余样本作为待诊断数据用于测试模型分类准确率。
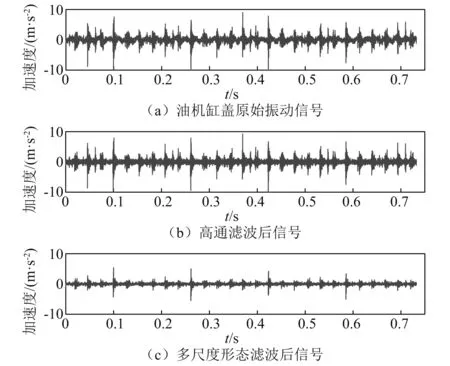
图3 振动信号降噪结果Fig.3 Result of noise reduction for vibration signal

图4 KPCA降维结果Fig.4 Result of dimension reduction by KPCA
4.2 基于自适应PSO的初始参数优化
初始观测值转移概率矩阵B的取值对隐马尔科夫模型的训练结果会产生较大影响,因此将HMM模型的初始参数B作为算法优化目标,以Forward-Backward算法作为适应度函数,计算每个粒子的输出似然概率值作为粒子适应度值。采用降维量化后的训练数据集进行算法的优化,并与标准PSO算法优化结果进行对比。两种算法对不同状态的模型初始参数优化结果如图5所示。

图5 各状态模型参数优化训练曲线Fig.5 Training curve of parameter optimization
从几种不同状态的模型参数优化曲线可以看出,与标准PSO算法相比,无论是在最终的适应度收敛值上,还是收敛速度方面,经过自适应改进的PSO算法表现都更加优异,证明自适应PSO算法的全局寻优能力要优于标准的PSO算法。
4.3 HMM模型训练与诊断结果
将选取的各状态训练数据集量化之后用于HMM模型训练,HMM模型状态数设置为3,量化级数设置为25,初始状态转移概率矩阵随机选取。将经过自适应PSO算法优化的结果作为Baum-Welch算法的初始参数,分别对油机正常状态、供气不足、进气门间隙异常的HMM模型进行训练。
训练完成之后,将剩余300组测试数据集分别输入已训练的各状态HMM模型,对训练的模型识别精度进行测试,并将测试结果与经标准PSO算法优化的HMM模型及传统HMM模型分类结果进行对比。传统HMM、标准PSO-HMM及自适应PSO-HMM的输出似然概率值如图6~8所示。
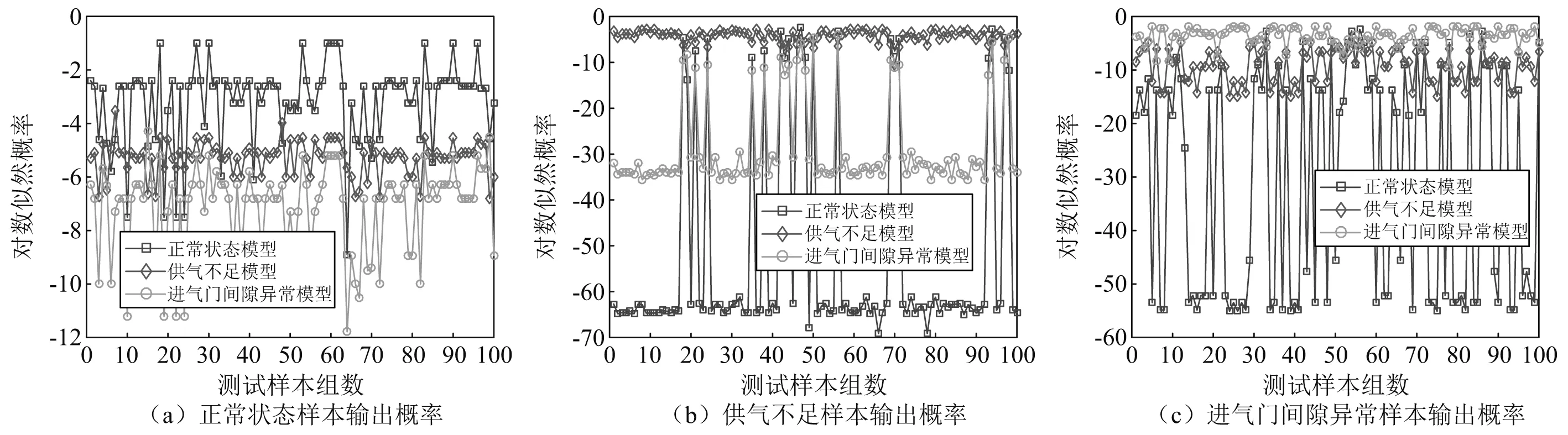
图6 传统HMM算法输出结果Fig.6 Output of traditional HMM

图7 标准PSO-HMM算法输出结果Fig.7 Output of standard PSO-HMM

图8 自适应PSO-HMM算法输出结果Fig.8 Output of adaptive PSO-HMM
根据输出似然概率值最大原则确定测试样本的故障诊断结果,并计算各算法的识别精度。同时采用支持向量机(SVM)算法用相同数据进行训练、测试,将诊断结果与自适应PSO-HMM算法识别结果进行对比分析。各算法分类正确率如表1所示,自适应PSO-HMM算法识别效果最优,标准PSO-HMM和经典SVM算法次之,传统HMM算法识别能力最弱。从中可以看出,引入群体智能优化算法能够提高传统HMM模型的诊断精度。并且经过自适应改进粒子群算法优化的HMM方法对油机电站的故障诊断精度要比标准PSO-HMM算法精度更高,其中油机正常状态的分类正确率提升了10%,供气不足的分类准确率提升了1%,进气门间隙异常的分类准确率提升了14%。整体分类准确率达到97.3%,与标准PSO-HMM相比提高了8.3%。此外,由于经典SVM算法中核函数及惩罚因子等参数的选择对模型诊断结果影响较大,因而模型识别能力要弱于自适应PSO-HMM算法。

表1 不同算法分类结果对比Tab.1 Diagnosis result of different algorithms
不同算法训练耗时如表2所示,由于群体智能优化算法的引入,HMM训练耗时有所增加,但前期对油机振动数据进行特征提取后采用KPCA方法进行降维处理,有效提升后续算法的训练效率,一定程度上降低了由于自适应PSO算法所带来的模型训练时间上的影响。而且,对标准PSO算法进行自适应改进后,能够更快找到全局最优值,有效减少算法迭代次数,缩短训练时长。模型训练完毕,采用相同数据集进行测试时,各算法的测试用时相差不大,均在5 s左右,说明算法的实用性。
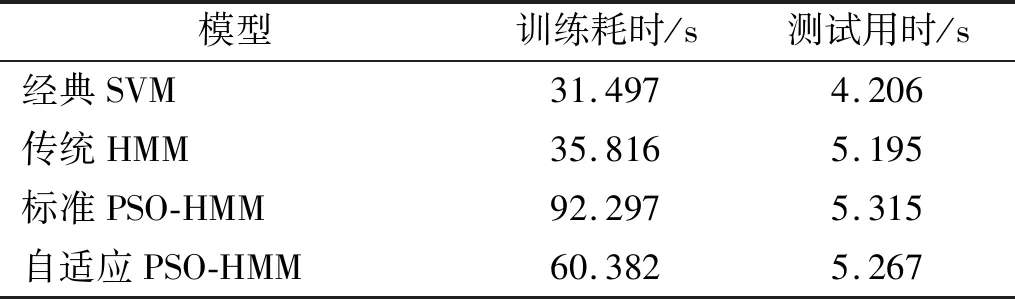
表2 不同算法耗时对比Tab.2 Execution time of different algorithms
5 结 论
本文提出了一种基于自适应粒子群优化的HMM故障诊断方法,对标准PSO算法进行了自适应改进,在此基础上对HMM初始参数进行了优化,并给出了基于自适应PSO-HMM的故障诊断流程。为了验证该方法的有效性,利用油机电站不同状态的实测振动数据,将自适应PSO-HMM与传统诊断方法进行了对比,得到以下结论:
(1)经过改进的自适应PSO算法较标准算法有更优的全局搜索能力和更快的收敛速度,模型训练耗时明显降低。
(2)自适应PSO-HMM的诊断精度比标准PSO-HMM更高,整体分类准确率能够达到97.3%,提高8%以上。
