适用于滞变性能退化结构体系抗震设计的新型侧向力模式

2021-11-10白久林孙博豪金双双

振动与冲击 2021年20期

白久林，孙博豪，金双双

(1.重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045；2.重庆大学土木工程学院，重庆 400045；3.重庆交通大学土木工程学院，重庆 400074)

传统结构抗震设计是根据作用在其上的侧向力进行弹性分析和能力设计，来获得结构竖向的强度和刚度分布，因此结构在强震下的抗震响应与结构的侧向力模式密切相关[1-2]。目前的设计侧向力模式主要是根据弹性结构系统的第一阶动力响应获得，强震下结构将进入非线性阶段，此时结构的层间剪力分布与通过侧向力模式设计的层间剪力差异较大，结构常出现不可控和非预期的地震失效模式(如薄弱层倒塌)，结构的抗震性能未能实现全局化和最大化[3-8]。

结构在强震下出现局部损伤失效，即结构的某些局部构件产生严重损伤，而其它构件处于弹性或损伤较低状态，这使得结构的材料性能未能充分发挥。由于地震动的往复效应使得损伤累积和加剧，最终由于损伤过大而使得结构的变形和损伤主要集中于某些局部楼层而失效。结构材料若从损伤较小部位转移到损伤较大部位，或将损伤严重部分进行加强，结构将获得均匀侧向变形的损伤状态，此时，不仅结构各部位的材料得到了充分利用，由于结构各部位均能耗能，结构的地震响应有望降低，结构的抗倒塌性能大幅提高，这就是均匀损伤设计的基本理念[3,5,8]。

基于均匀化损伤抗震理念[8-12]，诸多新型侧向力模式已形成和发展。Hajirasouliha等[13]基于层剪切模型，在对结构动力特性进行均匀损伤优化设计的基础上，提出了能考虑结构周期和设计目标延性的新侧向力模式。Park等[4]为使结构获得各楼层变形相同的均匀损伤模式，根据层模型结构的层间剪力需求，发展了新侧向力模式。Chao等[6]根据实体框架结构在多条地震下的最大层间剪力分布，提取并发展了基于结构非线性状态的新的侧向力模式。为考虑土-结构动力相互作用效应(SSI)，Ganjavi等[5]提出了弹性层剪切结构新型侧向力模式。孙国华等[14]、李慎等[15]、郝际平等[16]通过时程分析方法，分别对钢框架-钢板剪力墙结构、高强钢组合K形偏心支撑钢框架、半刚性框架-屈曲约束钢板剪力墙结构的层剪力分布进行了研究，将提取的层剪力分布模式结果按照我国规范模式拟合，并证实了剪力分布模式相较于其他规范形式具有更高的精度。此外，Li等[17]、Ganjavi等[18]也对新型侧向力模式进行了相关研究。

可以看出，目前的新型侧向力模式主要基于多层剪切模型[3,5,8,13,17,18]和基于实体结构模型[6,14-16]来获得。当采用实体结构模型来获得新型侧向力模式时，由于需要优化迭代，分析的结构数目偏少，且分析结果的普适性有限。因此，在获取新型侧向力模式时，多层剪切模型的适用性更为广泛。需要指出的是，基于多层剪切模型发展的新型侧向力模式，主要是基于弹性系统或性能非退化的弹塑性本构模型[5,7,8,13,18]。对于性能退化结构，如钢筋混凝土结构等，其强度/刚度退化、滞回曲线捏缩，基于均匀损伤优化来获取新型侧向力，目前还未见报道。基于此，本文提出了适用于性能退化结构体系抗震设计的新型侧向力模式，基于峰值指向性改进I-K模型[19]，发展了剪切模型的均匀损伤优化设计程序，系统研究了目标延性、周期、地震动、阻尼比、材料延性能力等参数对新型侧向力模式的影响。基于主要影响参数，提出了新型侧向力模式的量化表达式，可为性能退化结构的抗震设计提供依据和参考。

1 结构分析模型

在用来研究结构非线性响应的众多模型中，剪切模型是被广泛采用的模型之一，其可靠性和准确性已被验证[1]。剪切模型中各楼层的质量集中在楼层处，楼层仅发生水平位移，不考虑结构的弯曲变形，楼层之间采用非线性单元来连接，其分析模型如图1所示。由于剪切模型的简化性和计算分析的高效性[20-21]，易于优化设计和参数分析，因此本文采用剪切模型来获取新型侧向力模式，并基于OpenSees平台来进行非线性分析[22]。需再次指出的是，在获取新型侧向力模式时，也可采用实体结构来进行分析[6]，但由于优化需要不断更改结构设计参数，一般分析的结构数目较少，且分析结果往往不具有一般性。

图1 结构分析模型示意图Fig.1 Schematic diagram of structural analysis model

剪切模型的核心在于连接楼层的非线性单元。由于本文考虑的是性能退化结构的新型侧向力模式，层间连接单元采用峰值指向型改进I-K模型[18]。改进I-K模型既能考虑强度退化、卸载刚度退化又能考虑捏缩效应，有三种不同的材料模型，分别为双线型、峰值指向型和捏缩型。由于双线型材料模型不能模拟构件的捏拢效应，而峰值指向型材料模型既能考虑捏拢效应且相较于捏拢型材料模型拥有较少的参数，能够真实模拟性能退化结构的滞回特性，因此本文选用峰值指向型改进I-K模型作为分析模型，其骨架曲线和滞回曲线如图2所示。

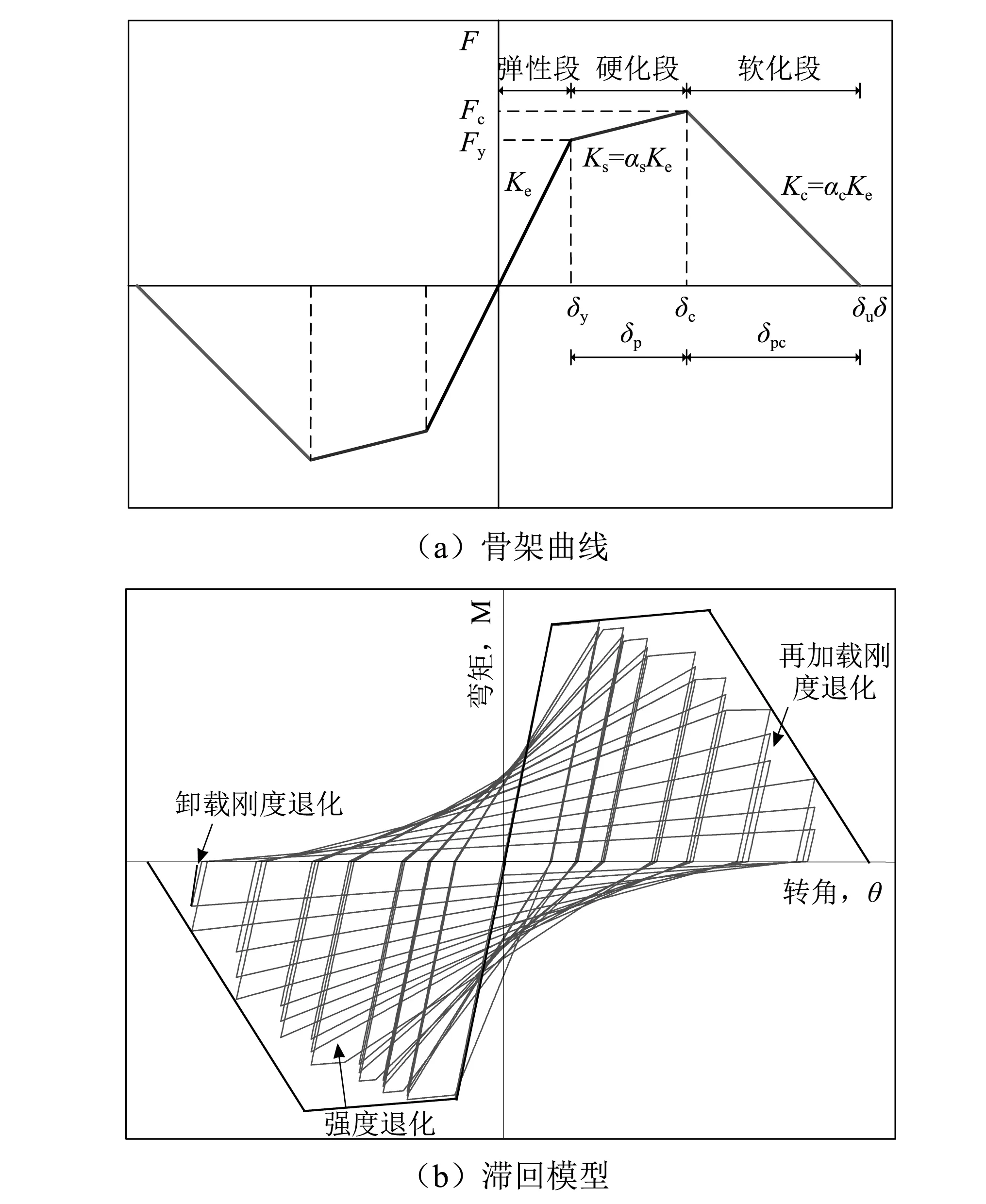
图2 峰值指向型改进I-K模型Fig.2 The modified I-K material model with peak-oriented

从图中可知，峰值指向型改进I-K模型的骨架曲线为三段式，分别为弹性段、硬化段和软化段。图中Ke、Ks(Ks=αsKe)、Kc(Kc=αcKe)分别为弹性刚度、硬化刚度和软化刚度，αs、αc分别为硬化刚度系数和软化刚度系数，δy、δp、δpc分别为弹性段位移、硬化段位移和软化段位移，Fy和Fc分别屈服荷载和峰值荷载，δc和δu分别为峰值荷载对应的位移和极限位移。通过改变峰值指向型改进I-K模型中的相关参数，可获得具有不同特征的材料恢复力模型。陶静[23]对不同模型参数的影响规律进行了详细研究，指出影响峰值指向型改进I-K模型的主要因素为软化刚度、材料延性能力和材料循环退化系数。

软化刚度Kc主要通过软化刚度系数αc控制，本文选取αc分别为-0.1、-0.3和-0.5来代表小、中和大三种软化刚度。材料延性能力指峰值强度对应的位移与屈服位移的比值，即δc/δy；本文选取δc/δy分别为2、4和6来代表低、中等和超强三种延性水平。材料循环退化系数γs,c,a,k的大小可改变材料在循环加载作用下的退化程度，本文分别考虑慢速退化(γs,c,a=100、γk=200)、中速退化(γs,c,a=50、γk=100)和快速退化(γs,c,a=25、γk=50)三组参数。

2 均匀损伤优化设计

2.1 优化要素

为了使本文建立的分析模型通过优化设计的手段，获得性能退化结构的新型侧向力模式，需做如下合理假定。

(1)假设剪切模型的楼层质量沿楼高均匀分布，且每层的质量均设置为100 t。结构每层的层高均为3.6 m。结构的层间屈服位移角设置为0.3%，则结构的屈服位移δy为10.8 mm。根据性能退化结构的实际情况，目标延性μt最大值取为5，且考虑1、1.5、2、3、4和5共6种情况。需要指出的是，结构的屈服层间位移角一般约0.3%～0.6%，我国抗震规范对框架类结构的大震层间位移角限值设定为2%，根据延性系数的定义可计算出大震设计时的延性系数为3.3～6.7。综合考虑，本文最大目标延性μt取为5。

(2)假设结构的基本周期Tfix为楼层数的0.1倍，即Tfix=0.1n，n为楼层总数。本文选择3、5、8、10、12、15、17和20层共8种结构，其对应的基本周期分别为0.3 s、0.5 s、0.8 s、1 s、1.2 s、1.5 s、1.7 s和2 s。

(3)假设结构的刚度沿楼层高度线性分布，且在优化过程中楼层弹性刚度保持不变。这一假定是基于本文的分析模型主要是针对滞变性能退化的结构体系，如混凝土结构等，优化主要处理截面的配筋设计，而截面尺寸一般保持不变。因此，结构的刚度变化不大。为使结构的刚度调整到预期值，需根据初始结构周期来进行缩放：

(1)

式中：Ktotal,1和Ktotal,0分别为优化结构的总刚度和初始结构的总刚度，T0和Ttarget分别为初始结构和优化结构的基本周期。

(4)剪切模型的层剪力可根据抗震分析获得，层间剪力的差即为作用在楼层上的侧向力，进而侧向力模式可计算出：

(2)

Fi=Si/Vbase

(3)

式中：i为楼层数，Vi为第i层的剪力，Si为第i层的楼层剪力差即侧向力，Vbase为基底剪力，Fi为侧向力分布模式。

(5)为考虑结构可能遭受到的地震作用，本文采用SIMQKE软件[24]合成了21条人工地震动，并以此作为输入来优化结构。合成原则为人工地震动的反应谱与我国抗震规范反应谱在[0-6]s的周期段能最大程度的拟合。图3(a)给出了其中某条地震动的加速度时程曲线，图3(b)为人工地震动的加速度反应谱及其平均值与规范值的对比。可以看出，规范谱与人工合成地震动具有较好的匹配。需说明的是，本文是基于均匀损伤的思想来发展新型侧向力分布模式，其应具有普适性，满足大部分工况要求，因此选择21条符合我国抗震规范谱的人工地震动作为输入来优化结构。若选用多条天然地震动，其频谱特性一般差异大，获得的结构地震响应离散型明显，导致最终获得的侧向力模式不具代表性。

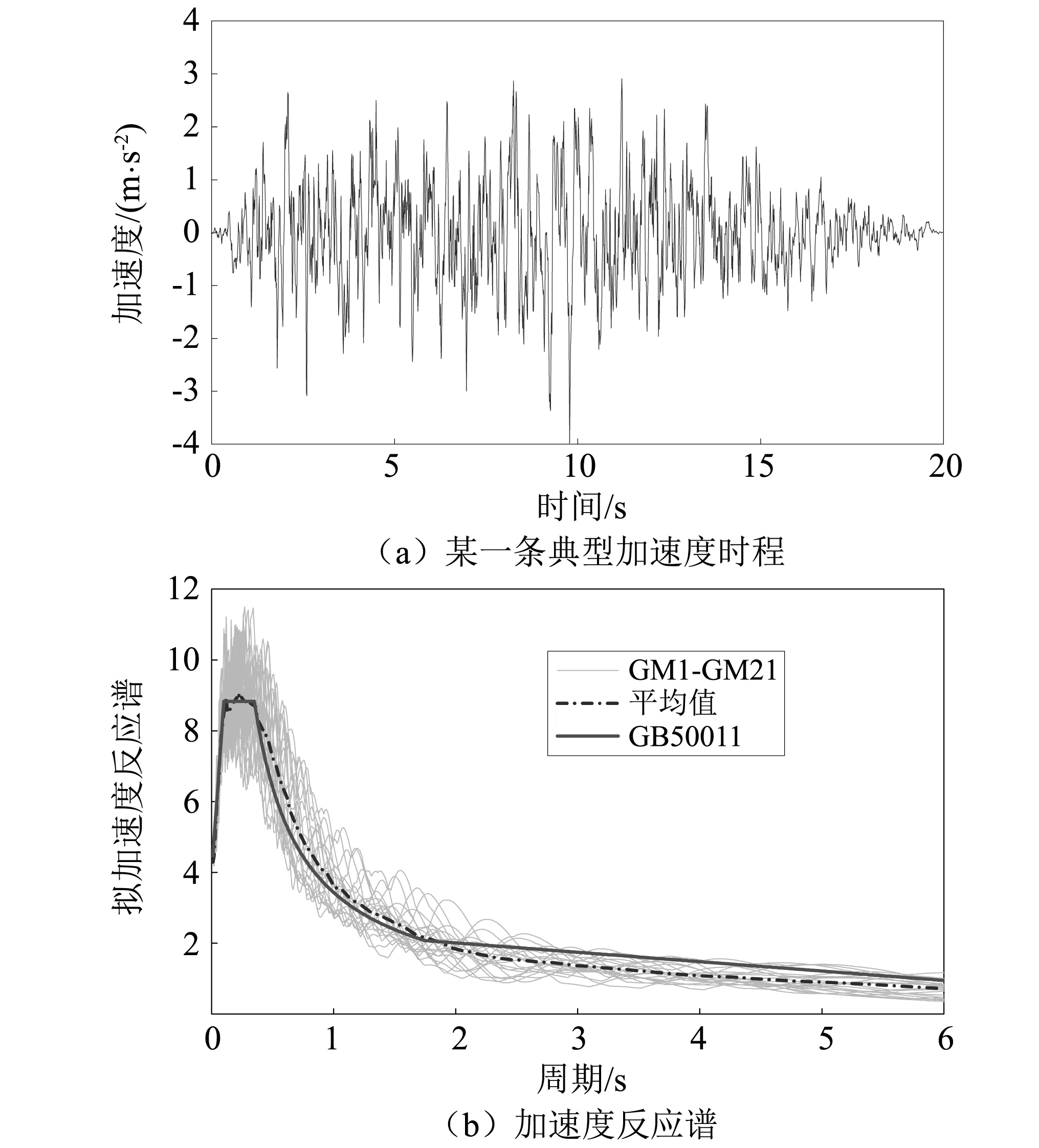
图3 人工地震动Fig.3 Artificial ground motions

2.2 优化设计的构建

从以上分析可知，本文在优化过程中，结构的刚度保持不变，仅对结构的强度进行优化，即对屈服强度Fy进行优化。为防止结构某些楼层严重破坏或失效，优化设计的目标为使结构在地震作用下的损伤达到均匀分布。已有研究指出[7-9]，当结构材料从损伤轻微部分转移到损伤严重部位直至获得均匀的竖向损伤分布状态时，结构将形成全局化和整体化的耗能机制，结构的抗震性能将得到提高。本文选择楼层位移延性作为损伤指标，以楼层均匀损伤分布为优化目标：

(4)

(5)

式中：f为优化目标函数，COVμ和COVμ0分别为优化结构和原始结构楼层延性系数的变异系数，μstd和μmean分别为楼层延性系数的标准差和平均值。

在优化过程中，假定结构的材料成本保持不变，此可近似为结构的总强度保持不变：

(Fy,total)j+1=(Fy,total)

(6)

式中：Fy,total为结构各层的强度之和，j为优化迭代步数。

随着优化的进行，结构的延性分布逐渐趋于均匀，当COVμ小于2%时，即认为结构获得了均匀损伤分布，整个优化过程停止。

2.3 优化过程

均匀损伤优化程序的主要步骤如下：

步骤1选定初始的结构参数，包括结构楼层数、基本周期Tfix以及峰值指向型改进I-K模型的相关参数。

步骤2根据线性刚度分布假设和公式(1)迭代缩放结构的总刚度，使结构周期达到步骤1的预设值。在优化过程中，结构的刚度始终保持不变。

步骤3根据结构各层的刚度和假定的楼层屈服位移δy，计算结构各楼层的初始强度和总强度。

步骤4输入地震动对结构进行非线性时程分析，初始地震动的峰值加速度取为200 gal。

步骤5计算结构各层的延性系数μi和平均值μmean。

步骤6判断是否满足收敛条件。

步骤7若不收敛，采用式(7)重新计算结构各层的强度。

(7)

式中：Fyi为第i层的屈服强度，α为收敛参数。在保持强度分布比例不变的条件下，根据约束条件式(6)再次调整结构各层的强度。并返回步骤4。可以看出，当结构损伤较小(延性μi较低)时，根据式(7)，结构的强度(材料)将减少，反之损伤较大时，结构的强度(材料)将增加。这样，通过式(7)的计算，便实现了结构材料从损伤较小部位转移到损伤较大部位。

步骤8若收敛，则此时通过式(2)和(3)计算的侧向力分布模式即为当前条件下的最优侧向力分布模式，此时的目标延性μt即为步骤5计算的μmean。由此可见，随着地震动强震的增大，优化所得的目标延性也会逐渐增大，本文设置地震动强度每次增大20 gal。若目标延性大于等于5时，则结束整个优化程序；若目标延性小于5，则增大地震动强度，并返回步骤4。显然，此时计算得到的目标延性(即优化后的μmean)并非前文设定的目标延性值μt。所以还需对目标延性进行线性插值，来获得目标延性所对应的最优侧向力分布模式。整个优化的流程如图4所示。

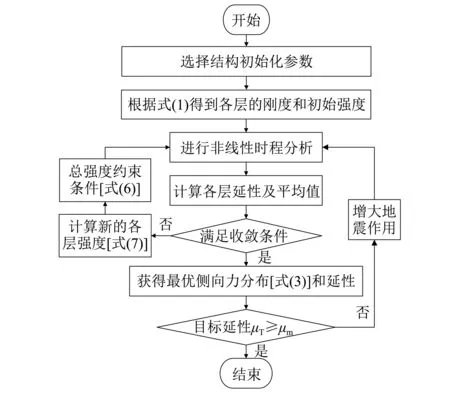
图4 优化流程图Fig.4 Optimization the flow chart

3 参数分析

在本文所提的均匀损伤优化设计方法中，有诸多参数将会对优化结果产生影响，如收敛参数的取值、地震激励、目标延性值、本构模型参数等。因此，有必要对这些参数进行详细的参数分析，并获得这些参数的影响规律。

3.1 收敛参数

在均匀损伤优化设计中，不同的收敛参数会直接影响优化收敛速度和收敛效果。以基本周期Tfix=1 s、目标延性μt=2的模型为例，在地震动GM1作用下，将收敛参数α分别设置为0.02，0.05，0.08和0.1进行优化，目标函数随迭代步数的变化情况如图5所示。可以看出，随着优化过程的不断进行，目标函数有减小的趋势，在优化过程的前几步，除α=0.1以外，目标函数都逐渐减小且降速在前几步最快。此外，随着收敛参数数值的增加，收敛速度越快，所需要的迭代步数较少。当α=0.08时，在前几步目标函数下降，之后目标函数增加；当α=0.1时，目标函数一直增大，表明结构的损伤一直是向着不均匀分布的方向发展。此外，从图中还可以看出，当优化过程能收敛时，无论收敛参数的取值为多少，目标函数的收敛值是大致相同的。这也表明，结构的优化结果和损伤分布的均匀程度在能收敛的情况下是大致相同的，与收敛参数的取值关系不大。综合收敛稳定性和收敛速度两方面考虑，本文建议收敛参数α取值范围在0.02～0.05之间。

图5 不同收敛参数对优化结果的影响Fig.5 Influence of different converging parameter on the final solution

3.2 地震动

图6给出了基本周期Tfix=1 s、目标延性μt=1时，在21条地震作用下得到的新型侧向力分布模式以及其平均值。可以看出，不同地震动下获得的新型侧向力分布模式差别较大，新型侧向力分布模式对地震动特性较为敏感。为减小地震动带来的影响，使新型侧向力分布模式能够适应不同的地震作用，本文采用多条地震动分析结果的平均值来获取新型侧向力分布模式。后文的分析结果，除特殊注明外，均为取平均值后的结果。

图6 地震动对新型侧向力分布模式的影响Fig.6 The influence of ground motion on optimum lateral force distribution pattern

3.3 目标延性

为研究目标延性对新型侧向力分布模式的影响，分别选取基本周期Tfix=1 s的10层结构和Tfix=2 s的20层结构，并将目标延性μt为1、3、5时的新型侧向力分布模式进行对比，如图7所示。可以看到，随着目标延性的增大，底部楼层的侧向力分布会逐渐增大，顶部楼层的侧向力分布逐渐减小，而中部楼层侧向力分布变化较小。

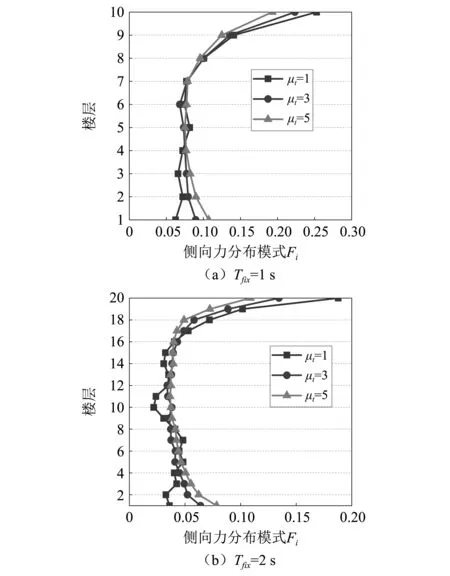
图7 目标延性对新型侧向力分布模式的影响Fig.7 The influence of target ductility on the optimum lateral force distribution pattern

3.4 基本周期

不同的楼层数对应不同的基本周期，为研究结构基本周期(楼层数)对侧向力分布模式的影响，图8给出了4种周期下楼层相对侧向力分布模式(各层侧向力分布与顶层侧向力分布的比值，Fi/Fn)随楼层相对高度(楼层高度除以结构总高)的关系曲线。可以看出，在顶层侧向力分布相等的情况下，不同基本周期的结构底部侧向力分布也大致相同，区别主要集中在结构中部，随着基本周期的增大，中部的侧向力分布逐渐减小。

图8 基本周期对新型侧向力分布模式的影响Fig.8 The influence of the fundamental period on the optimum lateral force distribution pattern

3.5 阻尼比的影响

图9给出了基本周期Tfix=1s、目标延性μt=2的结构在地震动GM1作用下，结构对应不同阻尼比时，获得的新型侧向力分布模式。可以看出，随着阻尼比的增加，顶部楼层的侧向力分布逐渐减小。其原因在于随着阻尼比的增加，主要影响顶层地震作用的高振型响应会相应降低。特别是在阻尼比小于5%时，结构中部和底部的侧向力分布区别较小。出于实际考虑，认为新型侧向力分布模式受阻尼比的影响不大，且本文的分析主要是针对混凝土类结构，因此将阻尼比设置为0.05。

图9 阻尼比对新型侧向力分布模式的影响Fig.9 Influence of damping ratio on optimum lateral force distribution pattern

3.6 软化刚度系数的影响

图10给出了在地震动GM1作用下，基本周期Tfix=1 s、目标延性μt=3、不同软化刚度系数结构获得的新型侧向力分布模式的对比。从图中可知不同软化刚度系数下的新型侧向力分布模式几乎完全重叠，软化刚度系数对新型侧向力分布模式几乎没有影响。在本文的研究中，将软化刚度系数统一定为-0.3。

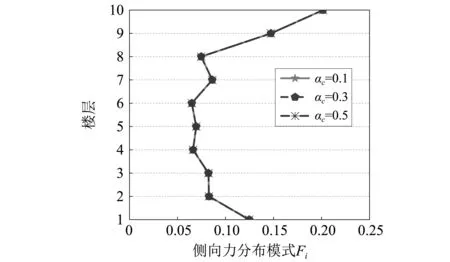
图10 软化刚度系数对新型侧向力分布模式的影响Fig.10 Influence of softening stiffness coefficient on optimum lateral force distribution pattern

3.7 材料延性能力的影响

图11给出了在地震动GM1作用下，基本周期Tfix为1 s、目标延性μt为3、不同材料延性能力时新型侧向力分布模式的对比。从图中可知目标延性μt增大时，材料延性能力对新型侧向力分布模式影响增加，特别是在结构目标延性较大(μt=4.7)，而材料延性能力较小(δc/δy=2)时。出于实际考虑，将材料延性能力设置为中等延性，即δc/δy=4。

图11 材料延性能力对新型侧向力分布模式的影响Fig.11 Influence of ductility on the optimum lateral force distribution pattern

3.8 材料循环退化速度的影响

图12给出了在地震动GM1作用下，基本周期为1 s、目标延性为3、不同材料循环退化速度时新型侧向力分布模式的对比。从图中可知不同材料循环退化速度下，新型侧向力分布模式之间的差别较小。因此在本文的分析研究中，将材料循环退化速度设置为中速退化。

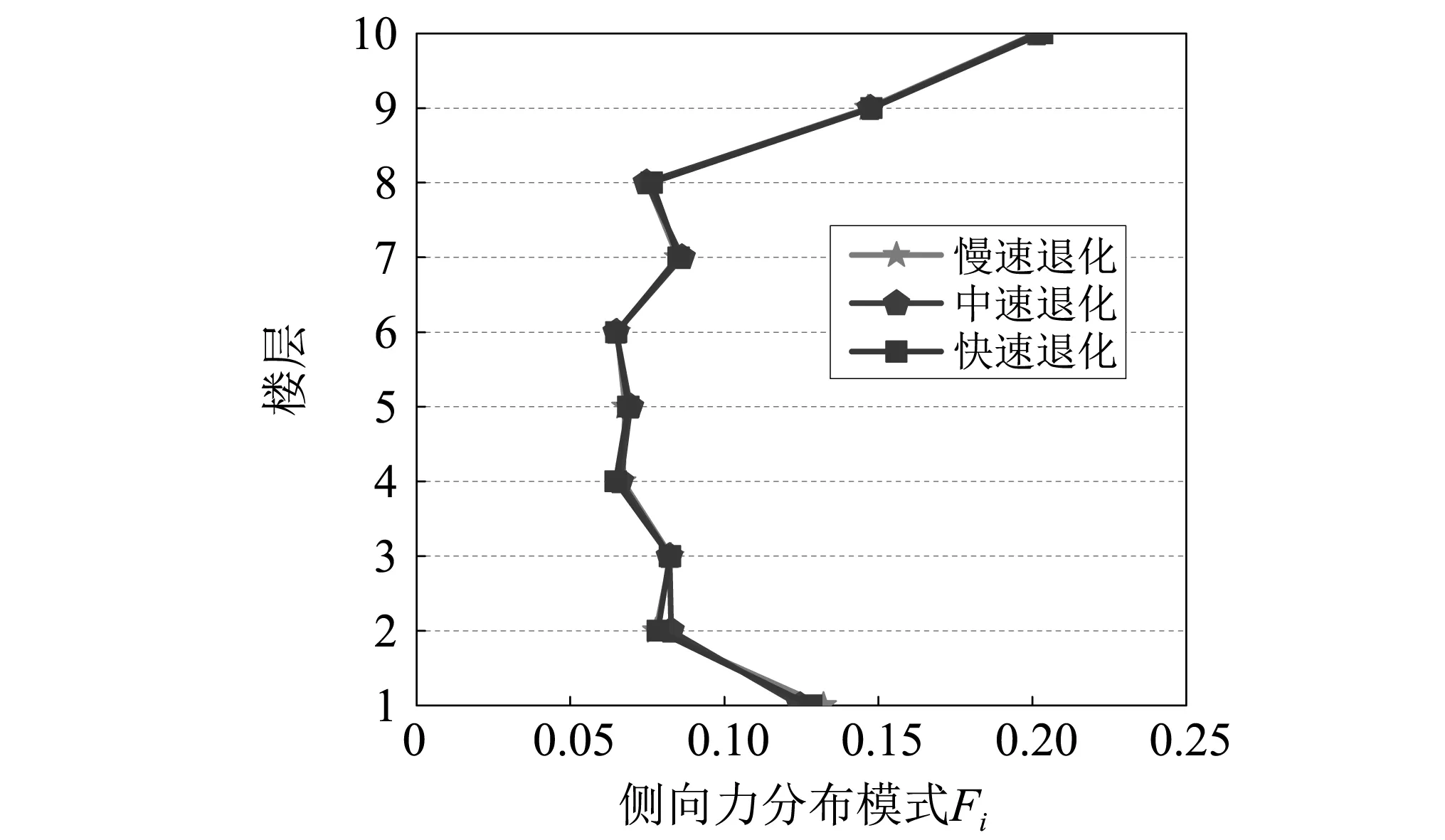
图12 材料循环退化速度对新型侧向力分布模式的影响Fig.12 Influence of material degradation rate on optimum lateral force distribution pattern

4 优化前后结构的抗震性能对比

图13是本文通过优化得到的新型侧向力分布模式(Tfix=1，μt=1.5)与我国规范侧向力模式的对比。可以看出，通过优化得到的新型侧向力分布模式与我国规范侧向力分布模式有明显的区别。就本例而言，主要表现在结构下部的侧向力分布增大，而结构中部的侧向力分布会相对减小。

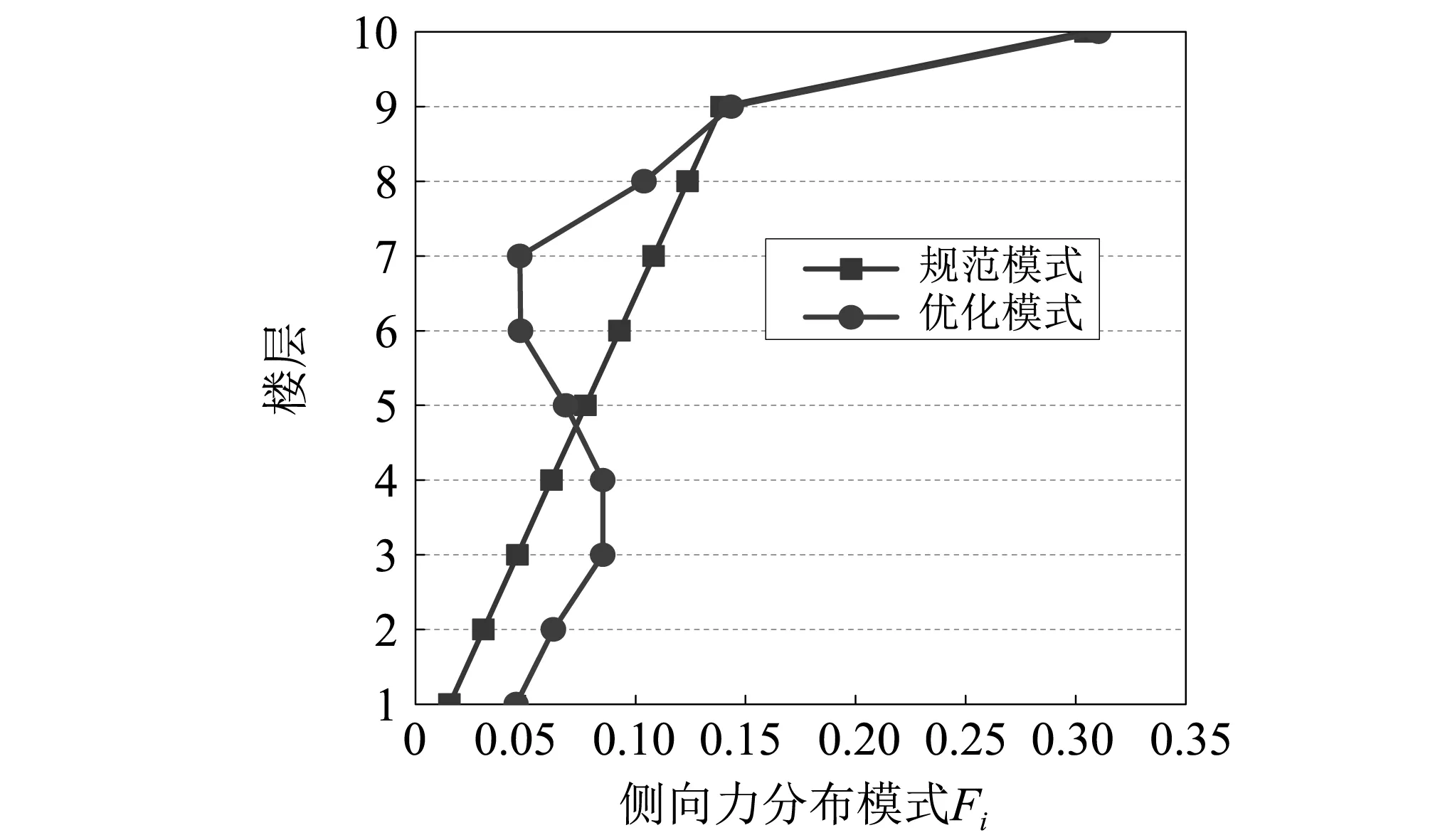
图13 新型侧向力分布模式和规范侧向力分布模式对比Fig.13 Comparison of optimum lateral force distribution pattern and standard lateral force distribution pattern

为验证通过本文优化方法得出的新型侧向力分布模式的有效性，在结构总强度相同的条件下，分别将剪切模型按新型侧向力分布模式和规范侧向力分布模式设计。以在地震动GM3作用下的计算结果为例，两种不同设计结构的各层延性系数对比如图14所示。从图中明显能看到，采用新型侧向力分布模式设计的结构，各层的延性系数实现了均匀化。而采用规范侧向力设计的结构则出现顶部和底部楼层延性明显比中部楼层延性偏大的现象，结构损伤出现了集中。这表明本文所提优化方法获得的新型侧向力模式，对实现结构的均匀损伤、增加结构的整体抗震性能。

图14 规范设计和优化设计下结构各层延性率对比Fig.14 Comparison of ductility ratio of different structures under standard design and optimization design

5 新型侧向力分布模式

(8)

式中：p1-p10为公式系数，其取值与目标延性μt有关，具体数值通过查表1查询获得。

表1 新型侧向力分布模式公式系数Tab.1 Coefficient formula of optimum lateral force distribution pattern

为验证本文所提出的拟合公式的准确性和有效性，选取三组不同的情况，将通过拟合公式得到的新型侧向力分布模式的计算值与真实值对比，结果如图15所示。从图中可知，三种情况的拟合效果均较好，拟合值与真实值差别较小。同时，拟合公式的相关系数大于0.99，这表明本文所提出的公式具有较高的精度，可在性能退化结构的抗震设计中应用。