基于CEL方法的航行体高速入水泡沫铝缓冲装置降载性能分析
2021-11-10孙龙泉王都亮李志鹏刘登科
孙龙泉,王都亮,李志鹏,刘登科
(哈尔滨工程大学 船舶工程学院,哈尔滨 150009)
结构物入水,如飞船返回舱入水[1]、飞机舱段入水[2]、空投鱼雷入水[3]等,都是涉及多相流动、自由液面和动边界多场耦合的复杂过程,其作用时间短暂,参数变化剧烈。尤其航行体高速入水时,结构会遭遇到强烈的瞬时冲击压力及过载,如果不进行缓冲降载,容易发生结构的损坏及内部器件的失灵,造成无法挽回的损失。因此研究高速入水降载技术意义重大。
在入水降载方面,Hinkley[4]首先提出在航行体头部加装头帽来保护航行体结构不受入水冲击载荷影响过大,入水冲击力使头罩破坏解体,不影响航行体本体正常工作。最初头帽为一个整体,经过发展改进,头帽分为外罩和缓冲材料两个部分,外罩起到在空中飞行阶段整流作用,缓冲材料起到隔冲降载、缓冲吸能、隔绝碎片的作用。在后续对头帽的研究中,宣建明等[5]通过入水试验,采用复合材料作为外罩的主体材料,研究了外罩的破坏形式。雷江涛等[6]通过有限元分析的方法,研究了头帽材料、壁厚和缓冲垫对航行器头帽分离可靠性的影响。徐新栋等[7]提出了两种使头帽入水后更易破裂的改进方法,一种为降低头帽和雷体之间的摩擦力,另一种为降低整流罩强度。并通过仿真计算的方式进行了验证。钱立新等[8]对带头帽的鱼雷的入水过程进行了数值模拟和实验验证,得出“撑进破坏”是带头罩鱼雷入水时头罩破坏的有效方式。预制槽弱链结构是实现“撑进破坏“方式的有效结构形式的结论。这些研究主要针对外罩的破坏模式,为外罩结构的设计提供理论基础,但对内部降载元件的设计及高速入水条件下的优化未做过多涉及。钱立新等[9]通过分析空气动力载荷和入水冲击载荷,提出了一种用切线法设计正切尖拱鱼雷头罩的可行域的方法。该研究对外罩结构尺寸的设计提供了可行参考。而针对内部降载元件的研究中,路龙龙[10]使用有限元软件ANSYS/LS-DYNA 计算了小角度入水和垂直入水时受到的入水载荷,提出了入水缓冲保护头帽的设计方案,简单分析了缓冲材料的质量和结构要求。王永虎等[11]采用入水冲击加载条件下的本构关系式,计算了带缓冲头帽入水的动态缓冲性能。讨论了不同入水速度、不同密度泡沫对缓冲效果的影响。王永虎[12]又引入硬质聚氨酯泡沫塑料(rigid polyurethane foams,RPUF)在冲击条件下的本构关系,并进行了相应修正,求出入水冲击响应本构关系式,得出了快速确定RPUF控制参数的方法。这些研究中未涉及到高速入水,并且工况较为单一,所做的工作仍不够充分,结论无法支持起入水工程应用研究。
基于上述原因,本文使用欧拉-拉格朗日耦合算法(CEL方法)建立航行体-空气-水流固耦合模型,分析在不同入水速度(50~150 m/s)下,多种泡沫铝材料在入水过程中的降载效果,探讨入水速度和最优泡沫铝参数之间的规律,为入水冲击结构降载设计提供参考。
1 模型建立
为了降低航行体入水冲击载荷,在航行体的头部加上缓冲材料,在航行体入水砰击到水面的瞬间,依靠缓冲材料压缩吸收能量,从而起到缓冲作用,降低砰击载荷对航行体的影响。
1.1 物理模型设计
泡沫铝是一种功能性很强的降载吸能材料,具有密度小、吸收冲击能力强、易加工、成形精度高等优点可用于抗冲击结构设计。相对密度μ(μ=ρ*/ρs,ρ*为泡沫铝表现密度,ρs为致密铝密度)范围一般为2%~60%,可由发泡工艺过程控制。带缓冲材料的航行体入水初始状态如图1所示。
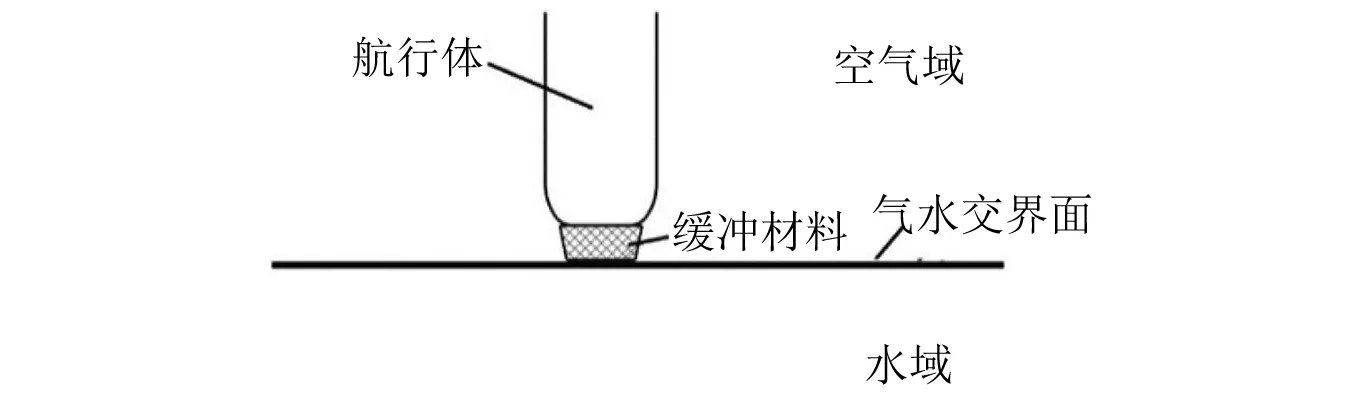
图1 带缓冲材料的航行体入水初始状态Fig.1 Initial state of water entry for a vehicle with buffer material
泡沫铝在压缩时,其应力应变曲线呈现明显的三阶段特征,即弹性变形阶段,塑性屈服平台阶段,压缩密实化阶段。泡沫铝典型的应力应变曲线如图2所示。
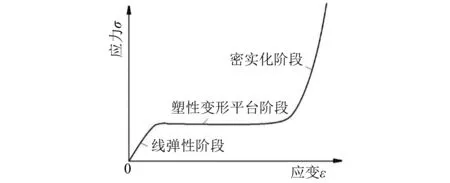
图2 泡沫铝的压缩应力应变曲线Fig.2 Compressive stress-strain curve of foamed aluminum
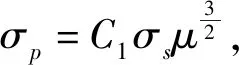
(1)
此方法计算出泡沫铝(μ=12.7%)的平台应力为4 MPa,εd为0.75,与文献[16]中的实验数据吻合较好。根据其拟合的经验公式,拟合出各相对密度下的应力应变曲线,如图 3所示。
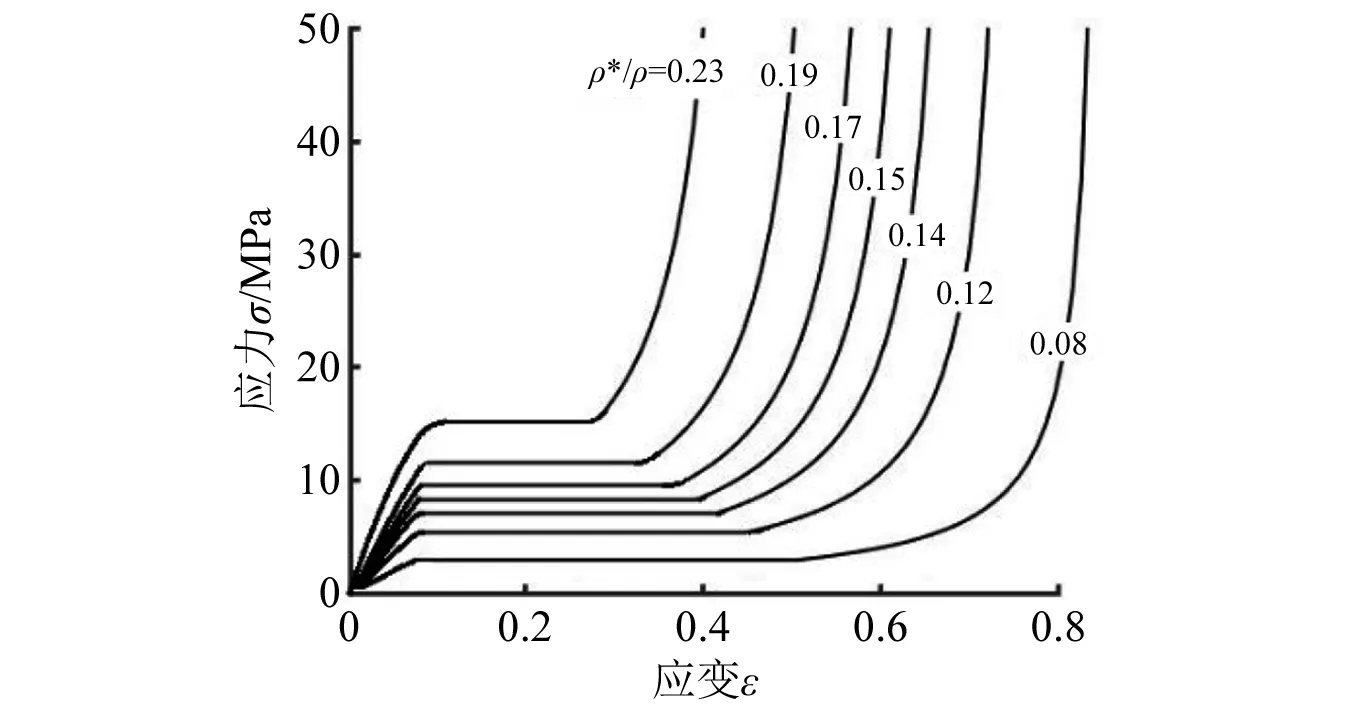
图3 不同相对密度泡沫铝的拟合应力应变曲线Fig.3 Fitting stress-strain curves of foamed aluminum with different relative densities
1.2 数值模型设计
采用耦合欧拉-拉格朗日方法,进行流固耦合求解,航行体和泡沫铝采用拉格朗日单元,空气域和水域采用欧拉单元。
选取MK46鱼雷作为需要降载的航行体,其长度为2.67 m,直径为0.324 m,重量为230 kg。
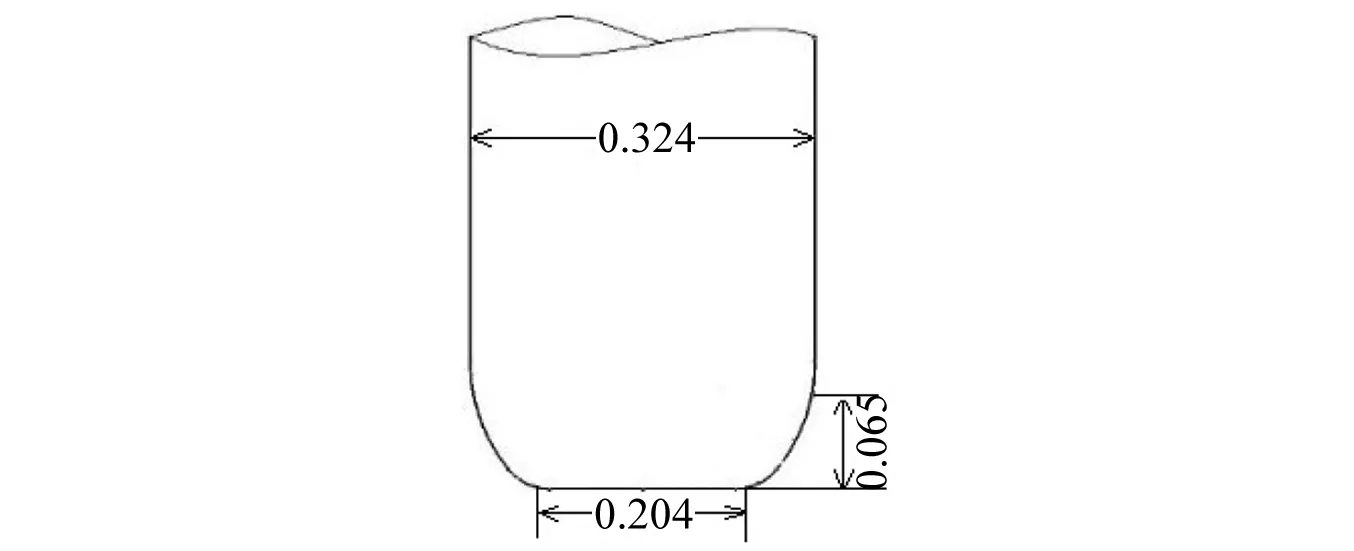
图4 MK46鱼雷模型头部形状尺寸(m)Fig.4 Head shape and size of MK46(m)
航行体建立可变形体,采用刚体(rigid body)约束,模型为空心,网格采用六面体结构化网格,保证航行体截面上至少有30个网格,网格尺寸设为0.02,网格数量为54 496,网格划分如图 5所示。材料为铝合金7075,参数如表 1所示。

表1 航行体材料参数Tab.1 Material parameters of vehicle

图5 航行体模型网格划分Fig.5 Mesh division of vehicle model
泡沫铝缓冲结构形状设计为圆台型,顶部半径0.12 m,底部半径0.1 m,高度0.1 m。材料模型设置采用软件中crushable foam塑性模型,该模型用于分析可压碎的泡沫,通常用作能量吸收结构。网格采用六面体结构化网格划分,单元类型为C3D8R,网格尺寸为0.01,数量为5 740。泡沫铝缓冲降载模型的建模及网格划分如图6所示。

图6 泡沫铝缓冲降载模型的建模及网格划分Fig.6 Mesh division of foam aluminum Buffer Load Reduction Model
欧拉域分为两部分,上侧部分为空气域,下侧部分为水域,为了提高计算效率,其网格在水气交界面进行加密,加密处网格采用渐进网格,靠近水气交界面处网格最密,最大程度的保证撞水时刻的计算精度,最密处网格尺寸设置0.015。权衡计算精度与计算资源消耗,结构体与欧拉域网格单元尺寸之比SR=1.5~2.0[18]。欧拉网格区域划分和网格划分如图7所示。
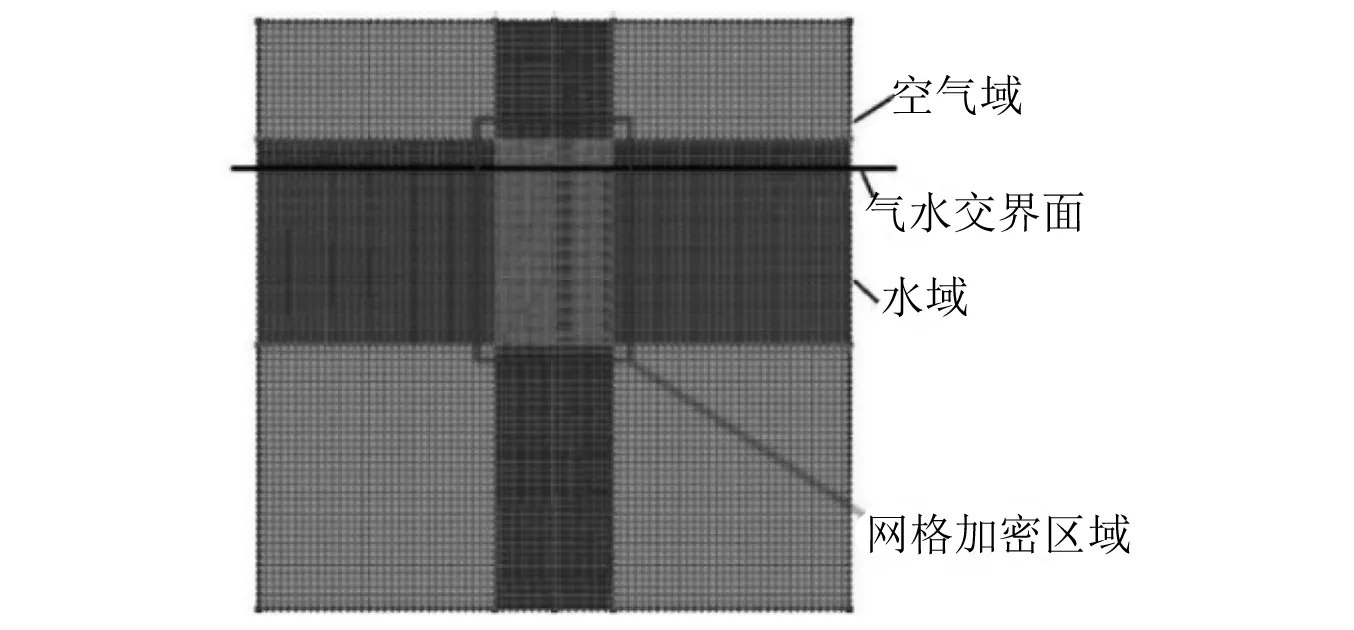
图7 欧拉域区域划分及网格划分Fig.7 Regionalization and mesh division of Euler Domain
初始时刻,航行体处于气水交界面上方,其装配示意图如图8所示。
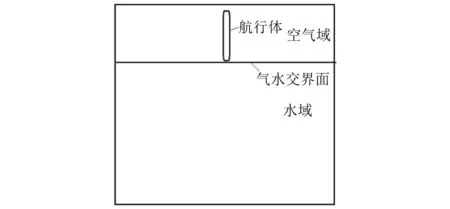
图8 入水模型装配图Fig.8 Assembly diagram of water entry model
欧拉域分水域和空气域,流体力学材料模型以状态方程的形式定义,状态方程可以确定材料的体积力。线性Hugoniot(Us-Up)状态方程可用于模拟由纳维尔-斯托克斯方程控制的黏性层流。水域是用Mie-Gruneisen状态方程的线性Hugoniot形式来模拟[17]。
Mie-Gruneisen状态方程通常用于模拟高压下的材料,是关于能量的线性方程,一般形式为
p-pH=Γρ(Em-EH)
(2)
式中:pH是Hugoniot的压力;EH为Hugoniot的比能。
Γ是Grüneisen比率,其值为Γ=Γ0ρ0/ρ,其中:Γ0为材料常数,ρ0为参考密度。EH可以用PH表示
(3)
式中:η=1-ρ0/ρ为名义体积压缩应变。
从上式中消去Γ和EH,得到
(4)
在每个物质点上需要同时求解状态方程和能量方程,它们表示压力和内能的耦合方程。
一般形式的Hugoniot数据的拟合曲线为
(5)
式中:c0和s是冲击波速度Us和质点速度Up之间关系的参数。
Us=c0+sUp
(6)
基于上述假设,线性Us-UpHugoniot式子可以写为
(7)
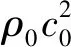

表2 水的材料参数Tab.2 Material parameters of water
空气域选取理想气体状态方程,其状态方程为
p+pA=ρR(θ-θZ)
(8)
式中:pA为周围环境压力,R为气体常数,θ为此刻温度,θZ为所用温度标尺的绝对零度。这是一种理想化的气体模型,可以近似地模拟适当条件下的任意气体。空气域的初始条件主要指定其初始密度ρ0,初始压力p0,周围环境压力pA,绝热质数γ,定容比热容cν,空气的材料参数如表3所示。

表3 空气材料参数Tab.3 Material parameters of air
欧拉域底面和四周固定,顶部施加大气压力,空气域内部设置101 325 Pa均匀压力,水域设置随深度变化的静水压力。设置重力加速度方向竖直向下。接触条件设为通用接触,物体之间设置摩擦因数为0.02。初始时刻航行体处在自由液面上方。
1.3 有效性验证
为验证CEL方法的有效性,采用数值仿真与文献[19]中圆柱体入水实验对比的方法,圆柱体直径42 mm,长度208 mm,质量为0.61 kg,以14.5 m/s的速度入水。实验中,采用phantom VEO 340S高速摄像机获取入水图像,使用TEMA软件对实验视频中模型上的标记点进行追踪,得到速度、加速度变化曲线。数值方法中,对圆柱体采用rigid body约束,提取头部中心点速度及加速度变化曲线,入水过程形态、速度曲线和加速度曲线如图9和图10所示。

图9 实验结果和数值模拟形态对比(t=1.67 ms,t=4.58 ms,t=7.50 ms,t=10.40 ms,t=13.33 ms)Fig.9 Comparison of experimental results and numerical simulation morphology
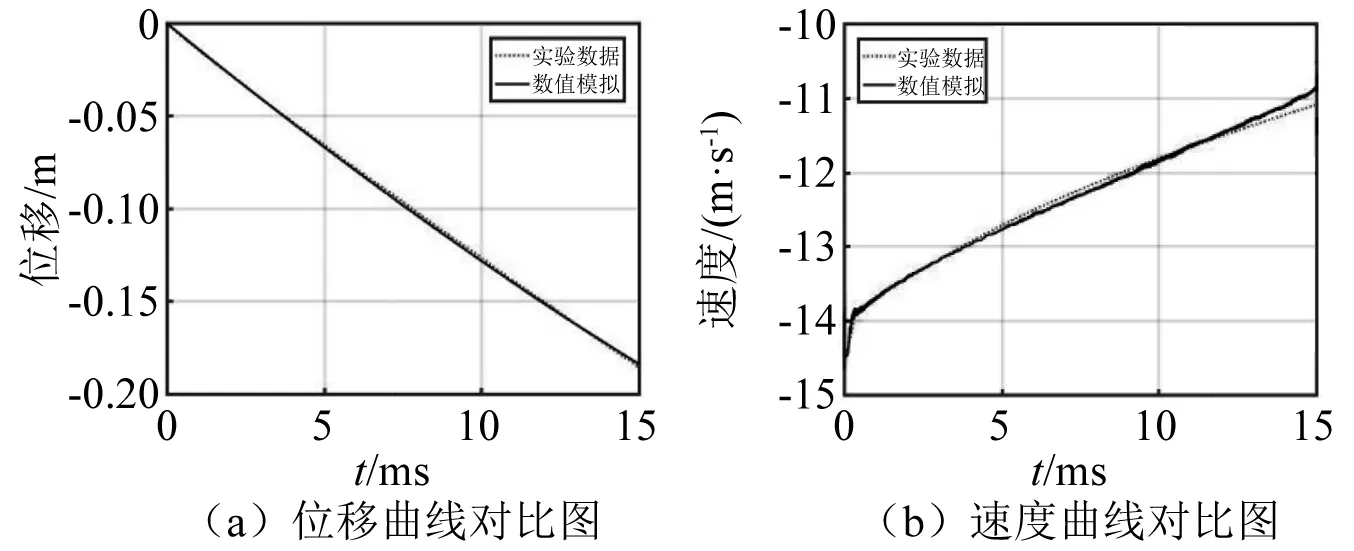
图10 数值模拟和实验结果运动参数对比Fig.10 Comparison of motion parameters between numerical simulation and experimental results
由数值模拟结果和实验结果对比中可以看出,CEL方法模拟得到的结果在运动参数和空泡形态都与实验结果吻合的比较好,在入水过程中的加速度变化趋势基本一致,且入水瞬间加速度峰值相差在10%以内。值得注意的是,从入水空泡发展形态、速度和加速度的变化情况看,在航行体入水“早期”,即约10 ms时间内,CEL方法模拟结果与实验符合程度较好,而在入水的“后期”,由于欧拉网格变形逐渐加大,累积误差不断增加,使空泡形态逐渐偏离,而且模拟中无法考虑空泡内部气体的运动和空化特性,导致入水“后期”数值误差较大。但从本文关注的入水冲击问题和加速度峰值出现的时间看,冲击峰值发生在航行体入水的“早期”,因此,可以认为本文所采用的CEL方法是合适的。
2 计算结果与分析
以泡沫铝作为缓冲材料,在航行体竖直入水过程中,依靠缓冲材料压缩吸收能量,提取航行体头部中心处加速度变化曲线,研究在不同相对密度的泡沫铝作为缓冲材料对降载效果的影响,进一步的,探究不同入水速度下的降载效果。
2.1 泡沫铝相对密度对航行体冲击性能的影响
泡沫铝缓冲结构随航行体以100 m/s的速度入水。选取相对密度为8%,12%,14%,15%,17%,19%,23%的泡沫铝进行计算,对入水过程进行数值分析,验证其降载效果。
图11为不同相对密度μ泡沫铝降载过程的加速度曲线。图12为带μ=17%的泡沫铝入水过程图,分别对应0 ms,0.625 ms,1.25 ms时刻。泡沫铝缓冲材料随航行体入水时,缓冲材料先接触到水面,入水阻力作用到缓冲材料上,受力压缩,进入短暂的弹性变形阶段,经由缓冲材料向航行体传递,缓冲材料向航行体传递的最大应力为泡沫铝材料的屈服应力极限σs,超过这个应力值时,泡沫铝材料即进入塑性变形阶段,将冲击能量吸收。此时向航行体传递的应力即为泡沫铝材料的平台应力σp,此时航行体的加速度曲线到达第一个峰值a1,图 11中每条加速度曲线从0.2 ms开始到0.8 ms都有一个台阶,此阶段即为泡沫铝材料的塑性应变阶段,此时航行体受到缓冲材料所传递的力即为泡沫铝材料的平台应力值。图13为泡沫铝前后受压变形对比,由于泡沫铝材料在此过程中,不是均匀压溃,靠近水面一侧压溃程度大于紧贴航行体头部一侧,泡沫铝中心受压程度明显大于四周,所以该阶段的加速度曲线呈现抖动。0.625 ms时刻,航行体的受力如图12(b)所示,由于泡沫铝材料在塑性变形阶段,缓冲材料向航行体传递的应力值几乎不变,为σp,所以在此段时间内加速度的变化量很小。随后缓冲材料继续压缩,直到泡沫铝材料塑性变形平台化阶段结束,进入密实化阶段,应力才会继续上升,同时,随着航行体入水深度的增加,1.25 ms时刻,航行体直接入水发生接触,部分入水阻力Fd直接加载在航行体上,此时刻的受力如图12(c)所示,航行体的加速度值在剩余能量的作用下达到第二个峰值a2,随后随着航行体入水深度的增加,加速度值减小,逐渐趋于稳定。
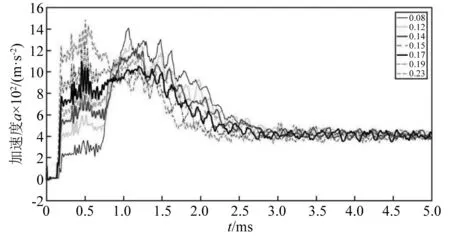
图11 不同μ泡沫铝降载过程的加速度曲线Fig.11 Acceleration curves of different μ foamed aluminum during load reduction
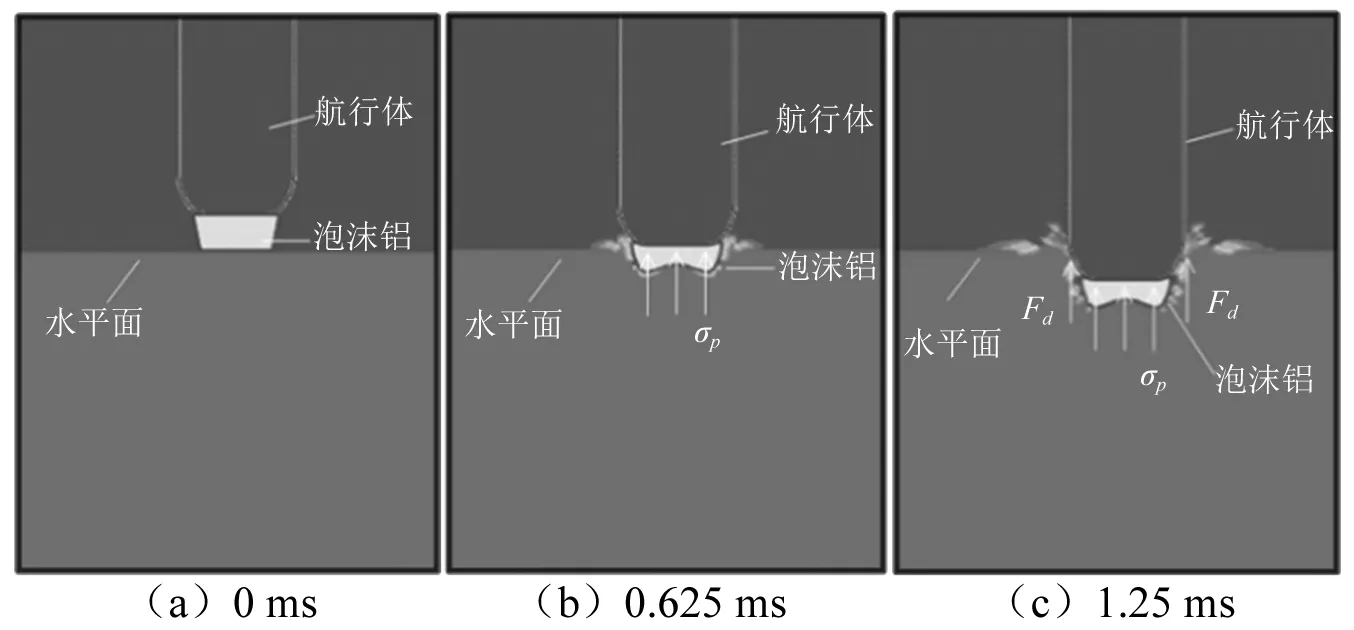
图12 航行体入水过程Fig.12 Water entry process of vehicle

图13 泡沫铝压缩变化对比Fig.13 Comparison of compression changes of foamed aluminum
表4列出了不同μ泡沫铝降载过程中加速度曲线的最大值,图14所示为表6中加速度峰值变化图。

表4 不同相对密度的泡沫铝降载后对应的加速度最大值Tab.4 The maximum acceleration of foam aluminum with different relative densities after load reduction
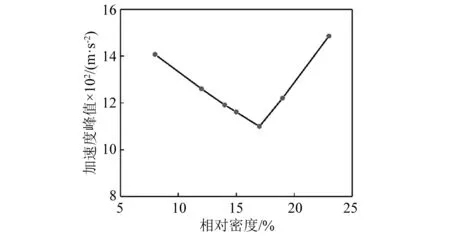
图14 不同泡沫铝降载后的加速度最大值变化图Fig.14 Maximum acceleration variation diagram after different foamed aluminum load reduction
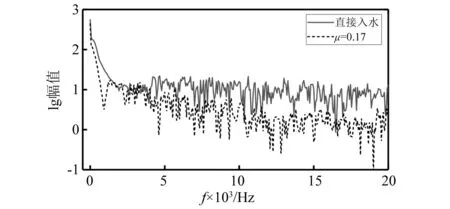
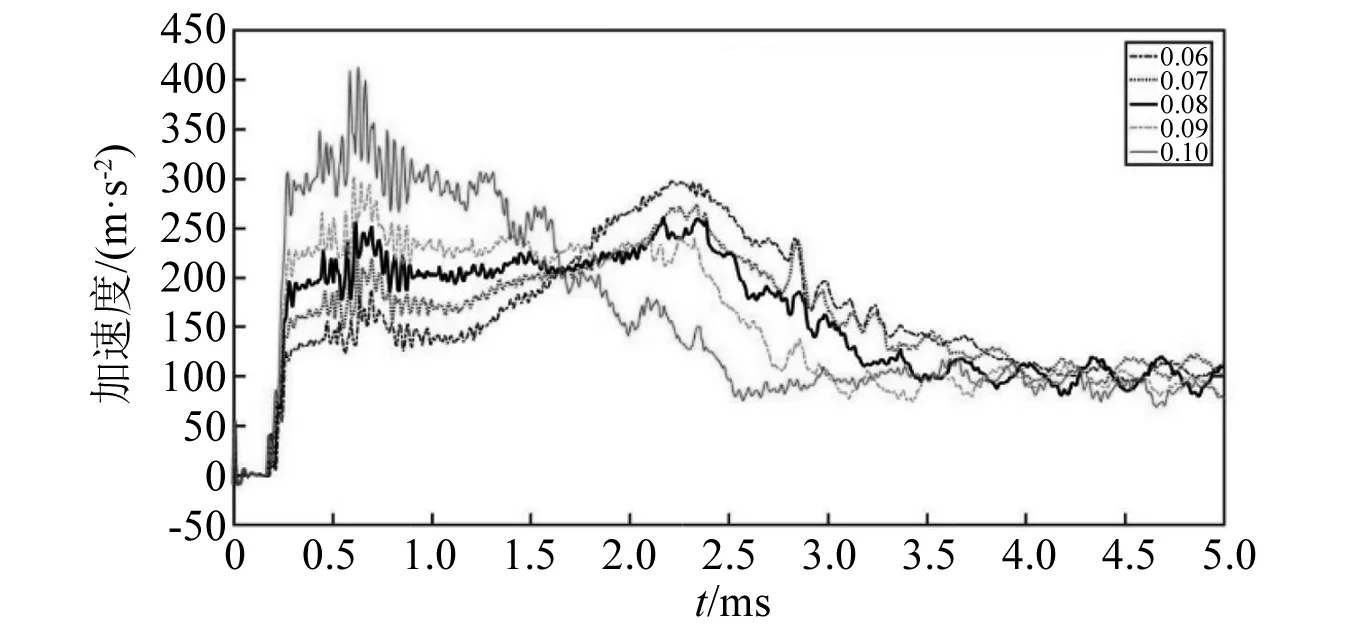
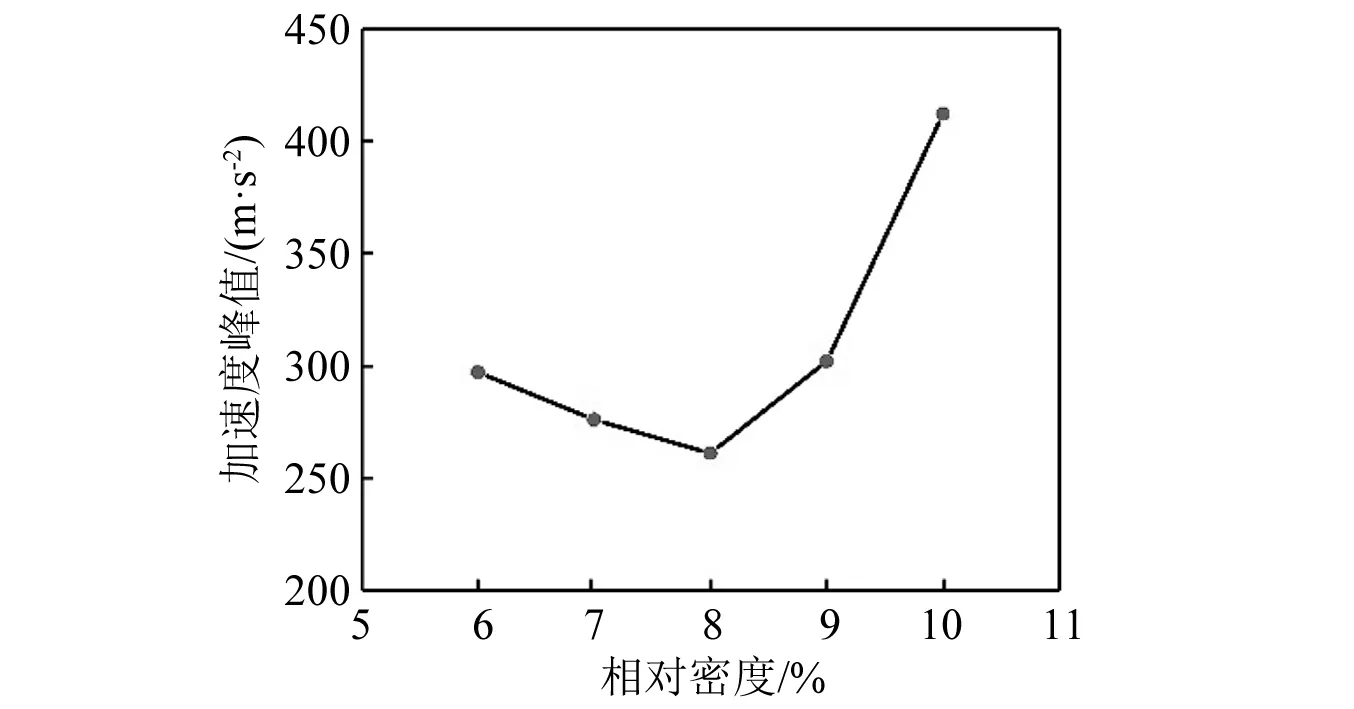
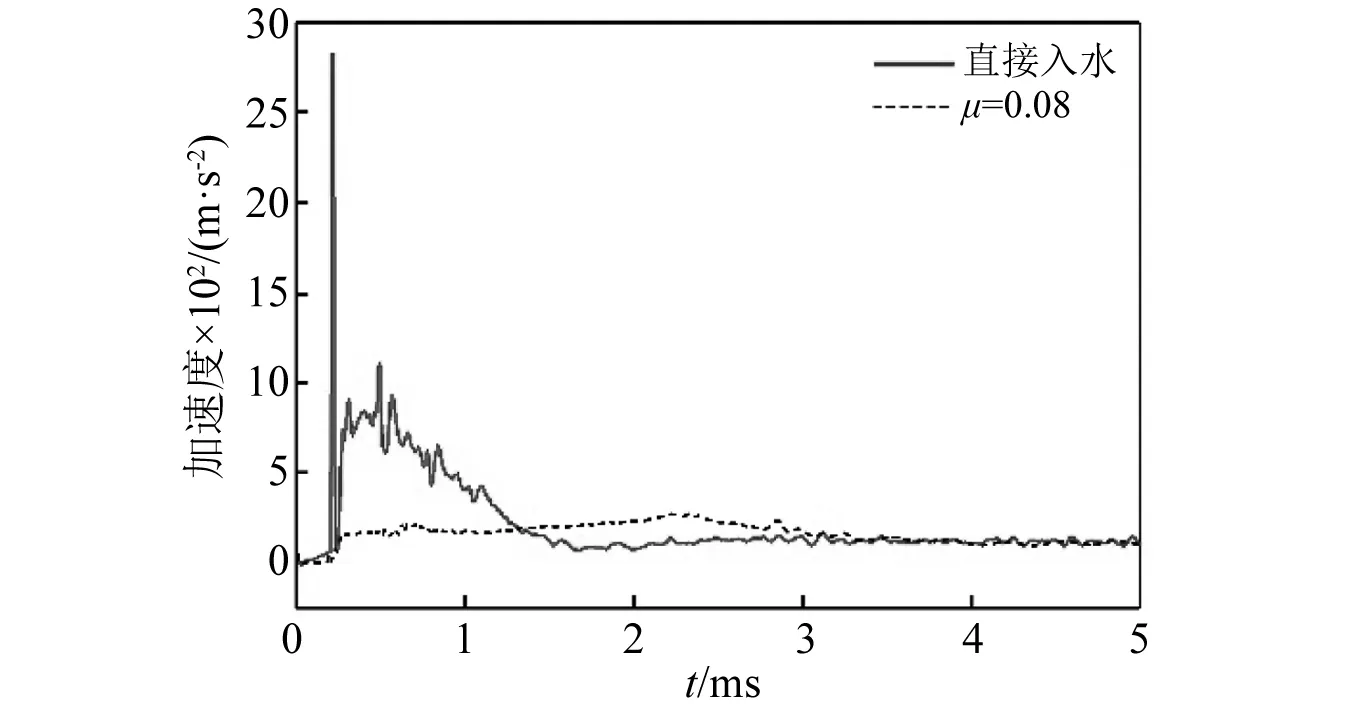
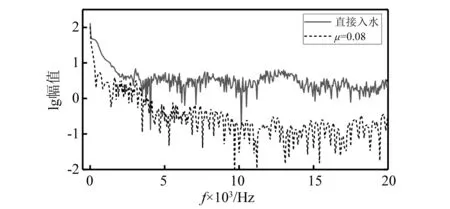
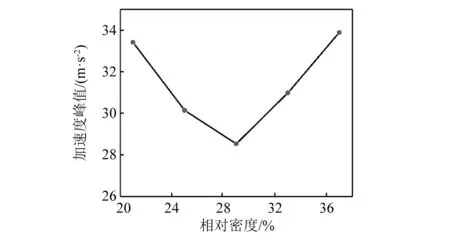
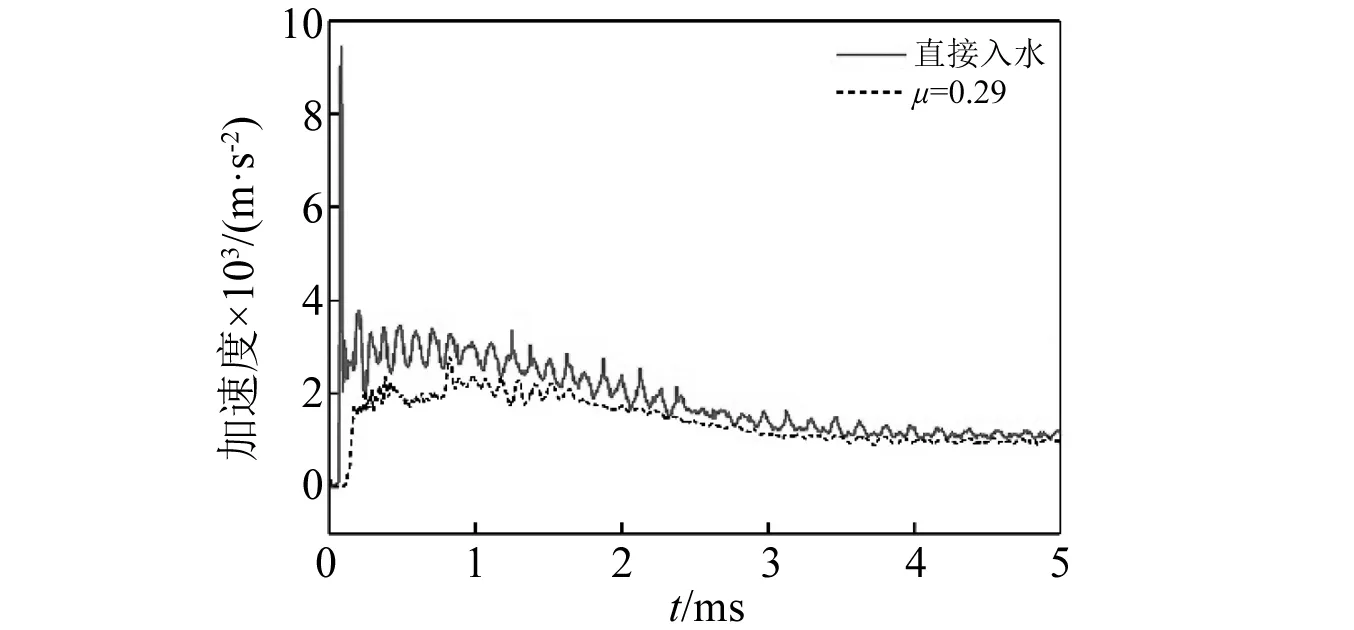
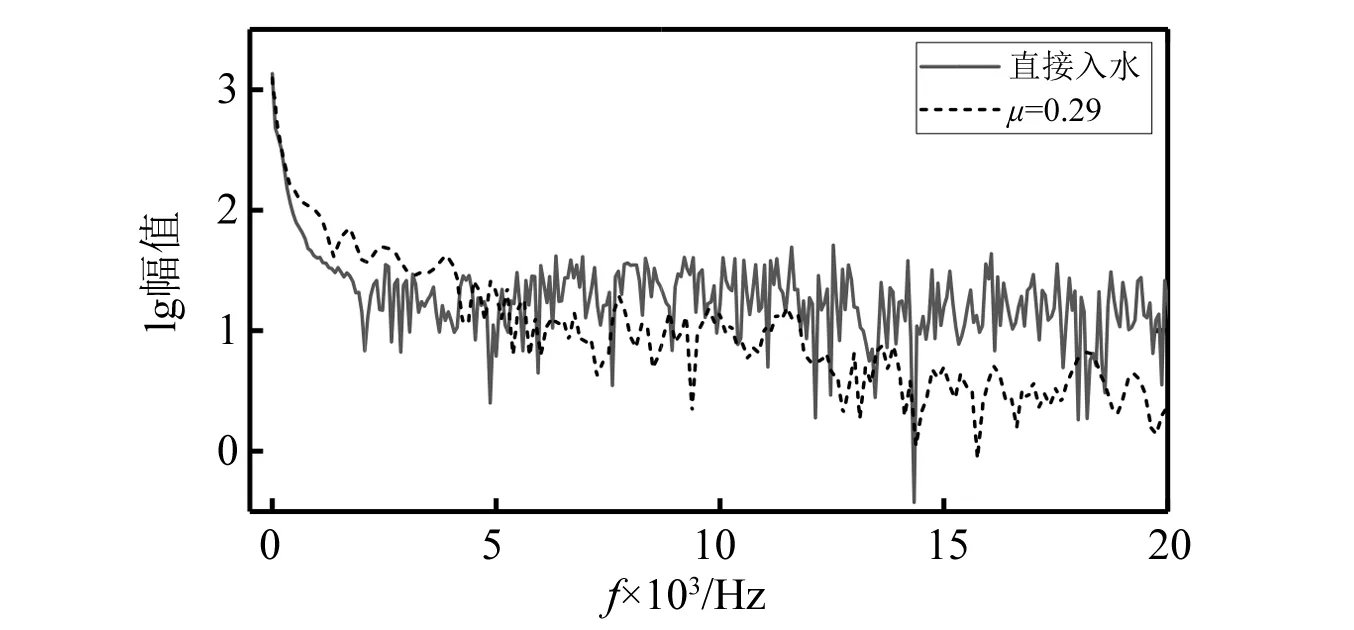
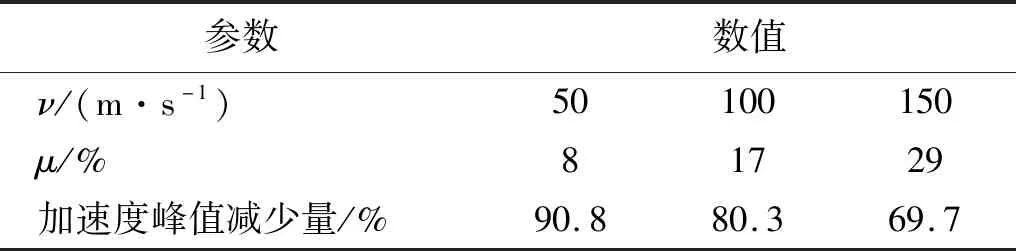
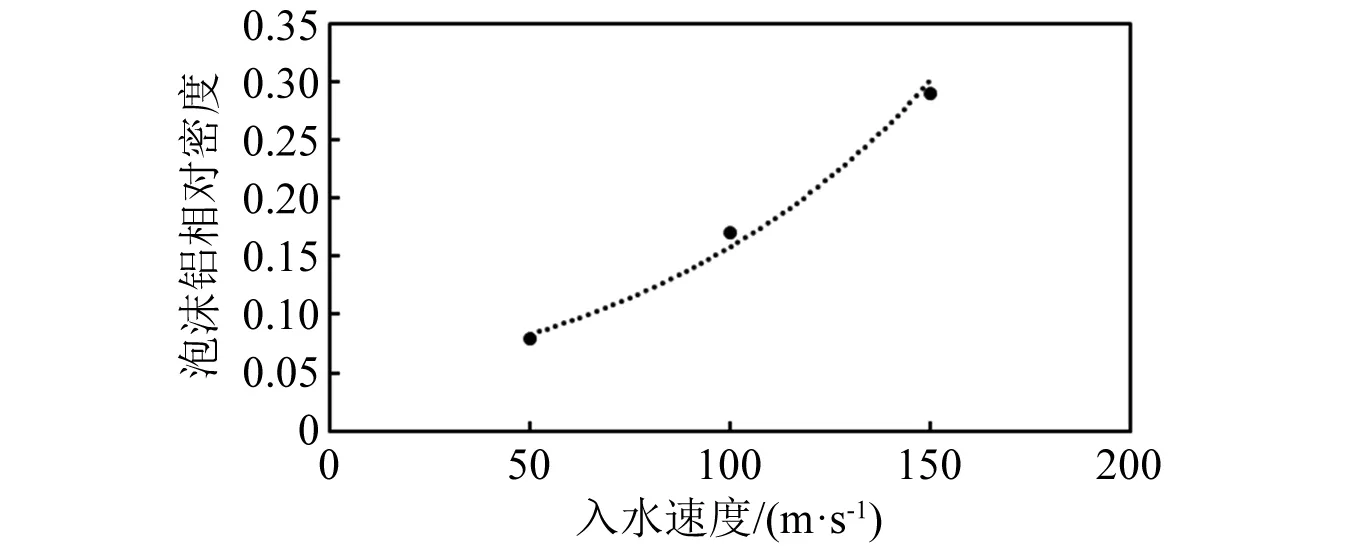
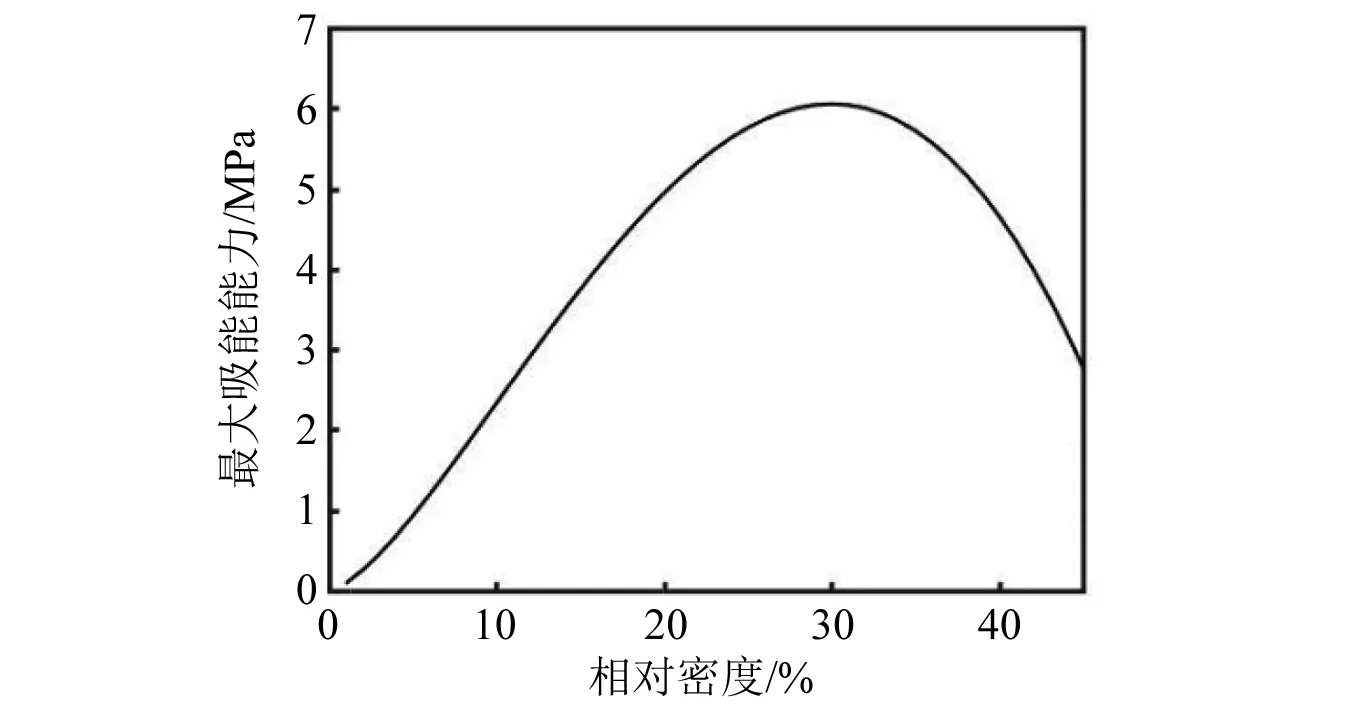
从图11中可以看出,泡沫铝材料的μ越大,即泡沫铝材料塑性阶段平台应力越大,进入塑性变形阶段时航行体的加速度值越大,即a1越大。这是由于μ越大,σp越大,缓冲材料传递给航行体的应力就会越大。而随着μ的增大,a2降低,说明随着μ增大,泡沫铝的吸能效果增加。当泡沫铝的μ较小时,a1 通过图14加速度最大值的对比可以看出,入水过程中航行体的最大加速度值随着泡沫铝材料的μ值增大先降低后升高,在μ=17%时达到最低,也就是说μ=17%时降载效果最好。这是由于μ偏小时,a1 将μ=17%的泡沫铝降载过程和航行体直接入水的加速度曲线进行对比,如图15所示。对加速度时历曲线进行傅里叶变换,得到的频谱曲线如图15所示(为突出曲线的变化,对纵坐标取lg对数)。 图15 带μ=17%的泡沫铝入水和直接入水的加速度对比Fig.15 Acceleration comparison of water entry with foamed aluminum μ=17% and direct water entry 入水后,泡沫铝材料受到入水阻力的作用,先进入短暂的弹性变形阶段,0.2 ms时刻,进入塑性变形阶段,冲击能量通过使泡沫铝塑性变形而吸收,起到降载作用。0.75 ms时刻,泡沫铝到达密实化阶段,继续产生很小的应变就对应的应力值很大,此时泡沫铝结构向航行体传递的应力也会迅速增加,且此时航行体头部沾湿,水开始对航行体施加阻力,随着航行体沾湿面积在速度方向上的投影面积增大,航行体在水中受到的阻力增大,到达1.25 ms时刻,航行体沾湿面积在速度方向上的投影面积达到最大,加速度达到峰值,为1 099 m/s2,之后随着航行体速度的降低,航行体受到水的阻力逐渐减小,到达2.5 ms左右时,加速度区域稳定,稳定值约为400 m/s2。航行体直接入水的加速度曲线峰值为5 566 m/s2,而带μ=17%的泡沫铝缓冲结构的航行体入水加速度峰值为1 099 m/s2,加速度的最大值降低80.3%。 图16中,在0频率时,直接入水要高于带泡沫铝入水,说明泡沫铝在入水过程吸收了一定的能量,直接入水曲线的峰值所在的频率要高于到泡沫铝入水。对比时历曲线与频率曲线,可以确定泡沫铝在降载过程中起到了吸能作用,并且优化载荷,降低冲击。 图16 带μ=17%的泡沫铝入水和直接入水的加速度频谱Fig.16 Acceleration frequency spectrum of water entry with foamed aluminum μ=17% and direct water entry 当航行体的入水速度不同时,入水时,缓冲材料受到入水冲击力的大小也会产生差异,降载材料的最优参数也会发生改变。带泡沫铝材料入水的航行体,加速度曲线中第一个加速度峰值和第二个加速度峰值基本相等时,降载效果达到最好。 2.2.1 50 m/s入水时的参数选择 选取μ分别为6%、7%、8%、9%,10%。对入水过程进行数值分析。 带不同相对μ铝材料以50 m/s的速度入水的加速度曲线对比如图17所示。图19为μ=8%的泡沫铝材料入水与直接入水的加速度对比图。对加速度进行傅里叶变换,得到图20中频谱曲线。 图17 不同μ泡沫铝降载过程加速度曲线对比图(50 m/s)Fig.17 Acceleration curves of different μ foamed aluminum during load reduction(50 m/s) 图18 不同μ泡沫铝降载过程加速度峰值变化曲线(50 m/s)Fig.18 Maximum acceleration variation diagram after different foamed aluminum load reduction(50 m/s) 图19 带μ=8%的泡沫铝入水和直接入水的加速度对比Fig.19 Acceleration comparison of water entry with foamed aluminum μ=8% and direct water entry 从图17可以看出,当第a1=a2时,加速度的最大值达到最低。图18为50 m/s入水时不同μ泡沫铝降载过程加速度峰值变化曲线,加速度的最大值随着μ的增大先降低后升高,在μ=8%时达到最低。通过对比得出,当μ=8%时,加速度最大值最低,为261 m/s2。入水速度为50 m/s时,μ=8%的泡沫铝材料对入水冲击载荷削峰效果最好。图20中,直接入水在0频率时峰值,以及其余峰值所在频率,都高于带泡沫铝入水。 图20 带μ=8%的泡沫铝入水和直接入水的加速度频谱Fig.20 Acceleration frequency spectrum of water entry with foamed aluminum μ=8% and direct water entry 2.2.2 150 m/s入水时的参数选择 带不同μ泡沫铝材料以150 m/s的速度入水的加速度曲线对比如图21所示。图23为带μ=29%的泡沫铝材料入水与直接入水的加速度对比图。图24中,对加速度进行傅里叶变换,得到其中频谱曲线。 图21 不同μ泡沫铝降载过程加速度曲线对比图(150 m/s)Fig.21 Acceleration curves of different μ foamed aluminum during load reduction(150 m/s) 当第a1=a2时从图21加速度对比图中可以看出,当μ分别为21%、25%、29%时,μ越大,a1越大,而a2越小,μ=33%时,a1随着泡沫铝的μ增加而增大,而a2没有明显减小,μ=37%,航行体第二个加速度峰值反而较μ=33%时的大。图22为150 m/s入水时不同μ泡沫铝降载过程加速度峰值变化曲线,加速度的最大值随着μ的增大先降低后升高,在μ=29%时达到最低,为2 853 m/s2。说明当入水速度为150 m/s时,μ=29%泡沫铝材料对入水冲击载荷削峰效果最好。 图22 不同μ泡沫铝降载过程加速度峰值变化曲线(150 m/s)Fig.22 Maximum acceleration variation diagram after different foamed aluminum load reduction(150 m/s) 图23 带μ=29%的泡沫铝入水和直接入水的加速度对比Fig.23 Acceleration comparison of water entry with foamed aluminum μ=29% and direct water entry 图24 带μ=29%的泡沫铝入水和直接入水的加速度频谱Fig.24 Acceleration frequency spectrum of water entry with foamed aluminum μ=29% and direct water entry 直接入水加速度频谱曲线与带泡沫铝入水相比,在0频率时峰值近似,曲线峰值所在频率更高。 不同入水速度下的最优泡沫铝材料的μ及其降载效果如表5所示。 表5 不同入水速度下的最优μ及降载效果Tab.5 Optimum μ and load reduction effect under different water entry speeds 图25为不同入水速度下最优μ,随着入水速度的增加,降载效果最好的泡沫铝材料的μ也随之增大,缓冲材料的降载效果随之降低。由前一节的分析可知,航行体达到第一个加速度峰值a1时,为泡沫铝材料进入塑性变形平台化阶段的时候,a1的大小即为平台应力与泡沫铝材料和航行体之间的接触面积的乘积除以航行体的质量,即a1=σp·A/m,其中A为泡沫铝材料和航行体之间的接触面积,m为航行体的质量。泡沫铝的μ越小,平台应力σp就越小,a1越小。a2则和航行体剩余动能有关,剩余动能越大,a2越大。 图25 不同入水速度下最优μFig.25 Optimal μ under different water entry speeds 泡沫铝单位体积到达密实化阶段时达到材料的最大吸能能力,此时吸收的最大能量由 (9) 得到。计算不同μ的泡沫铝最大吸收的能量,得到图22中最大吸能能力变化曲线。在μ<30%时,相对密度越大,泡沫铝的吸能能力就越好,塑性变形吸收的能量就越多,航行体的剩余能量就越小,第二个加速度峰值a2也就越小,当a1和a2达到平衡时,航行体加速度的最大值达到最低。 图26 最大吸能能力变化曲线Fig.26 Variation curve of maximum energy absorption capacity 当入水速度越小时,航行体的初始动能也就较小,经缓冲吸能后的剩余能量也就越小,此时第二个加速度峰值a2也越小,a1和a2的平衡点也就越低,所以入水速度越小,降载效果最好的泡沫铝材料的μ也就越低。 随着入水速度的增大,航行体初始动能随之增大,而缓冲材料的体积是一定的,虽然μ<30%时,随着降载效果最好的泡沫铝材料的相对密度的增加,其单位体积吸能能力有所增加,但其增幅远远低于航行体动能的增加量,故随着入水速度的增大,缓冲材料的缓冲效果降低。 本文采用了CEL方法,分析了泡沫铝的力学性能,研究了带缓冲材料航行体垂直入水时的动力响应问题,通过对μ不同的泡沫铝的缓冲效果进行了对比,讨论了对航行体在以一定速度入水时降载效果最好的泡沫铝参数优化问题,找到了入水速度和最优泡沫铝参数之间的规律,同时验证了最优参数泡沫铝的降载效果,表明缓冲材料的性能直接影响到航行体缓冲装置的降载效果。得出如下结论: (1)带缓冲材料的航行体入水时的受力过程存在两个峰值,第一个峰值a1与σp的大小有关,随着μ的增大而增大,第二个峰值a2与缓冲材料降载后的剩余动能有关,随着μ的增大而减小。当所选泡沫铝降载过程中,两个峰值基本相等时,则此μ为最优参数。 (2)泡沫铝的μ不同时,吸能效果不同,其降载性能随着μ的增加先升高再降低。当μ较小时,航行体受力过程中,a1 (3)入水速度越大时,降载效果最好的泡沫铝的μ越大。在缓冲材料的体积不能增加的情况下,入水速度越大,缓冲材料能起到的降载效果越低。 (4)缓冲材料能够避免航行体触水瞬间产生的瞬时巨大冲击力,并能降低后续头部入水阶段由于入水阻力产生的加速度峰值。在入水速度分别为50 m/s,100 m/s和150 m/s时,加速度最大值可以分别降低90.8%,80.3%和69.7%,具有良好的缓冲降载效果。研究结果对今后航行体入水降载研究具有一定的借鉴作用,有助于指导降载结构的设计。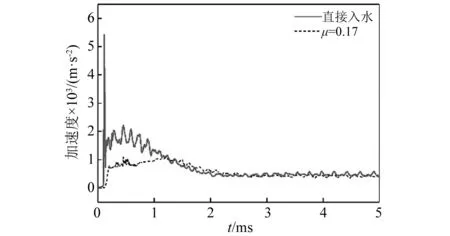
2.2 入水速度对带缓冲材料航行体冲击性能的影响

3 结 论
