基于共轭正态分布的抽样检验方案*
2021-11-10魏鹏辉秦桂香梁小林
魏鹏辉, 秦桂香, 梁小林
(长沙理工大学 数学与统计学院, 湖南 长沙 410114)
0 引言
抽样检验是可靠性理论中的一种假设检验方法,它是基于产品的生产与使用双方通过协商后的要求,用统计方法制定对一批该产品进行抽样与检验的方案,然后根据结果对这批产品进行接收或拒收.现在,大多数用户对产品的性能和可靠性要求越高越好,而要获得产品的性能指标和可靠性指标就需要对产品进行有效的样本检验[1].样本检验最直接方法是对所有产品进行检验,即全样本检验,但是对于很多产品来说,进行全样本检验是不现实的,因此通过部分抽样产品的样本性能指标去评价全部产品性能指标,就成了统计学中抽样检验理论的基本支撑.在许多种产品抽样检验中总是希望抽样量尽可能地少,例如破坏性检验.而经典统计方法制定的抽样检验方案的抽样量一般较大,因此我们需要运用新统计理论来制定更科学合理的抽样检验方案.由于Bayes方法能充分利用产品的各类验前信息、样本信息和总体信息,完成对产品的性能指标和可靠性指标的评估分析,所以应用Bayes方法来制定产品性能或可靠性的抽样检验方案不仅能优化计算步骤,而且能减少检验的抽样量.
关于产品性能指标服从正态分布的抽样检验方案的相关研究成果较少.张硕云等[2]对参数服从正态分布的装备在简单假设下,利用Bayes方法基于两类风险确定样本量.De Koker等[3]在岩土设计的材料参数确定中,利用预测可靠性指标,建立了明确考虑样本量的决策分析框架.该理论描述了最优样本容量、条件可靠性指标(通常作为目标值)与失效时的预期损伤之间的关系.冯文哲等[4]在复杂假设的情况下,基于0-1损失函数和两类风险为约束条件建立非线性约束规划模型.在考虑产品的指标有双侧规范限时,在上侧限和下侧限之间时产品是合格的,否则是不合格的.Wu等[5]开发了一种情境样本大小调整程序,称为紧-正-紧(TNT)抽样策略,产品性能的测量来自于具有双边规格限制的关键质量特征,遵循正态分布.参数由两个非线性不等式的联合解确定,这两个不等式满足可容忍的供应商风险、买方风险、期望的可接受质量水平(AQL)和极限质量水平(LQL).吴启光等[6]在综合双侧规格限下方差未知时,将服从正态分布的产品利用经典统计方法,通过生产方风险质量和使用方风险质量确定可靠性抽样检验方案.王燕飞[7]讨论了在正态分布指标的双侧规格限情形下,当总体方差已知,总体指标的均值为正时,依据Bayes方法,利用最大熵先验分布,求出后验分布.利用生产方和使用方的两类风险约束条件,确定最小抽检样本量,从而制定更加合理有效的抽样检验方案.
最大熵先验常常有部分先验信息可以利用,除此以外,部分要求尽可能采用无信息先验[8].这是在只有少量先验信息可以利用的情况下常被采用的方法.而现在我们却可以利用其他手段得到足够的先验信息,所以本文的主要工作是利用共轭先验法[9]得到产品指标值的后验分布,再利用生产方和使用方的两类风险约束条件,确定最大抽检样本量.通过算例说明经过了解的先验分布信息,只需要最多抽取少量的样本就可以得到能代表整体产品的指标信息,相较于最大熵先验的方法本方法确定的样本量较小,进而说明本方法是可行的,比经典统计方法更加有效和节约.
1 采用共轭分布法确定的抽样检验方案
设产品性能指标X~N(μ,σ2),其中σ2已知,指标均值μ>0未知.所抽取的样本为X1,X2,X3,…,Xn,观察值为x1,x2,x3,…,xn.根据生产方和使用方经过协商后设置指标综合双侧规格限,即规格下限L和规格上限U,如果产品的指标均值能够满足L≤μ≤U时我们认为是合格的,否则是不合格的.建立如下建设:
H0:L≤μ≤U
H1:μ>U或μ 定义1[10]设θ是总体分布p(x|θ)中的参数,π(θ)是θ的先验分布,如果对于任意来自p(x|θ)的样本观察值x1,x2,x3,…,xn得到的后验分布π(θ|x)与π(θ)属于同一分布族,则称其是θ的共轭先验分布. 证明事实上,假设x1,x2,x3,…,xn是来自正态分布N(μ,σ2)的样本观察值,则样本的似然函数为 根据贝叶斯定理,则μ的后验分布函数为 (1) 因此μ的后验分布为π(μ|t)=N(a,d2). 在确定抽检方案时,经常会遇到两种情况,即两种风险:生产方风险和使用方风险.对于生产方而言:在抽检中把合格的产品判别为不合格产品从而被拒绝(弃真)时的风险称为生产方风险,用α表示.对于使用方而言:在抽检中把不合格的产品判别为合格的产品从而被接收(取伪)时的风险称为使用方风险,用β表示. (2) 方程组(2)是一个抽样检验设计的模型,我们对其求解从而可以确定最大抽检样本量. 求解方程组首先要确定拒绝域W,根据Bayes假设检验理论,当后验概率 P(μ∈Θ1|T=t)≥P(μ∈Θ0|T=t) (3) 时拒绝原假设H0,其中Θ0是μ取双侧规格限之间,即μ∈[L,U],Θ1是μ取双侧规格限之外,即μ∈(-∞,L)∪(U,+∞).当t满足 (4) 时拒绝原假设H0,此时确定的t的范围就是拒绝域W. 利用Matlab编程来求得拒绝域W,具体的编程步骤为: 1) 首先建立函数 2) 建立两个程序 程序1: 程序2: 3) 运行两个程序可以分别得到临界点C1,C2. 我们可以得到T的拒绝域W=(0,C1)∪(C2,+∞),然后代入到方程组(2),得到最大检验样本量n. 在这里为了便于做出比较取相同的例子. 得出最大检验样本量为18. 表1 不同方法的比较结果 本文在王燕飞的成果基础上通过把只有少量信息的先验分布的最大熵先验改为当掌握比较多信息的先验分布的共轭先验分布,即正态分布,在其他已知条件不变的情况下,根据Bayes理论确定可靠性抽样检验方案.并通过Matlab软件编程搜索拒绝域的临界值,并由生产方和使用方的最大承担风险确定最大抽样样本量,所得到的结果与之相比较少,但是这是在多出一个参数的情况下所得出的优势,也就意味着在计算的时候过程会比较复杂.通过上面的算例可以得到经过了解的先验分布信息即服从正态分布,只需要最多抽取18个样本就可以得到比较能代表整体产品的信息.这种确定可靠性鉴定试验方案的方法是可行的,其最终得到的最小抽样检验量也小,更加节约经济,效果很好.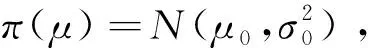
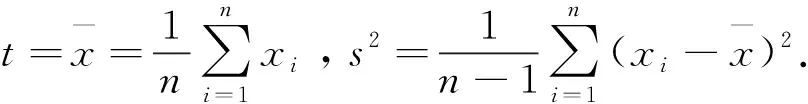
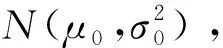
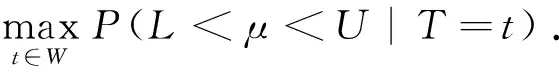
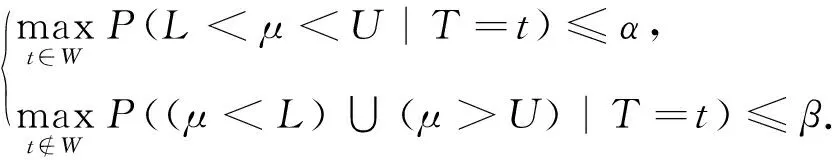
2 模型求解

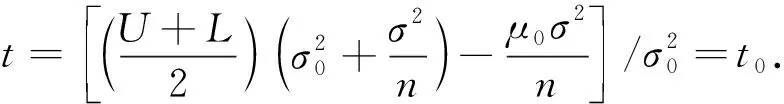
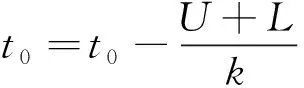
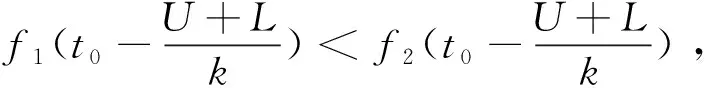
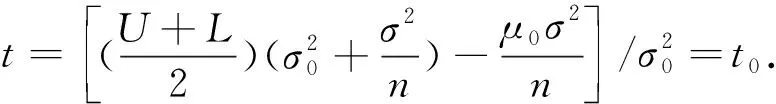
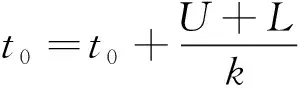
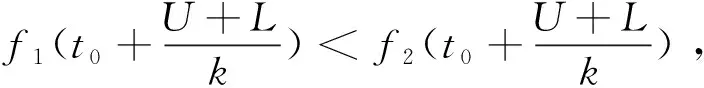
3 算例求解
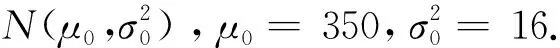
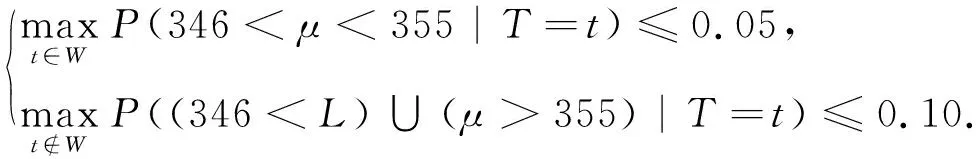

4 结论