如何求分段函数零点问题中的参数范围

山东省德州市第九中学 (253000) 李 琳

分段函数内容丰富、考点广泛、形式多样，是每年高考的热点.本文通过列举几个典型题例，介绍已知函数的零点个数的情况求其中的参数范围问题.

一、画出函数图像

图1

解析：因为f(x)是定义在R上的奇函数，所以f(-x)=-f(x)恒成立，即2-x+m·2x=-2x-m·2-x对任意x都成立，解得m=-1，所以

评注：函数图像是函数性质的直观体现，解题时如果能够画出函数的大致图像，并指出关键信息是非常有助于问题的解决．

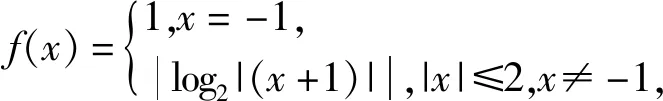
图2

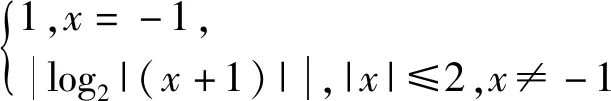
评注：由于此函数表达式含有两层绝对值，它的图像比较复杂，需要分步画出，故而如何画出大致的函数图像是解决问题的关键，对渐近线、特殊点必须标注清楚．

二、分类或分段讨论

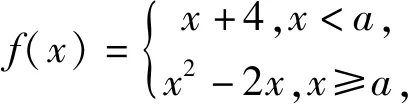
解析：在同一坐标系中分别画出y=x+4与y=x2-2x的图像分析可知，由于函数g(x)=f(x)-b都有零点，即方程f(x)=b都有解，即需f(x)的值域为R，当a≤1时，a+4≥1-2，解得a≥-5；当a>1时，a+4≥a2-2a，解得-1≤a≤4，综上所述.实数a的取值范围是[-5,4]．

评注：通过对参数进行逐一的分类讨论，再辅助于对应的函数图像分析，就可以得到对应不等关系，这也是比较实用有效的一个解题方法．

评注：由于给出的分段函数中需要对参数a进行讨论才能确定零点，即图像与x轴的交点，所以分类讨论是势在必行，关键注意如何确定分段的标准．

三、转化为解不等式

评注：欲求参数的取值范围，找到一个不等式是解决问题的常规思路，任何找是我们的主攻方向，本题中通过分析分段函数的零点情况，迅速地将问题转化为二次函数中的常见题型，这是解题的关键．

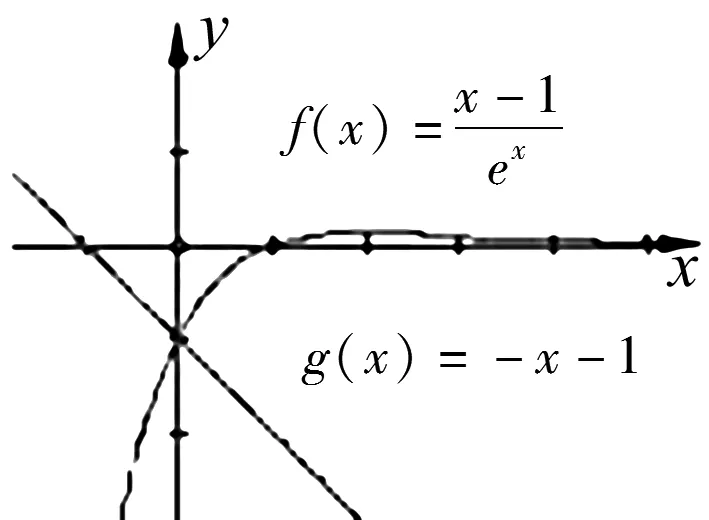
图3

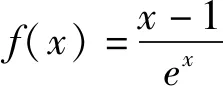
评注：本题主要考察了综合运用导数作函数图象的能力、零点判断及逆向思维能力等，其中利用导数作出函数的大致图象(特别是极值点和交的位置标注)是成功解题的关键．