对一道数列课堂习题的探究与引申

四川师范大学附属中学(高中) (610066) 周其祥 黄光鑫

四川师范大学数学科学学院 (610068) 纪定春

1.问题呈现

该数列证明题，主要考察学生对等差数列中等差中项的概念理解与应用，是培养学生数学概念理解能力、逻辑推理素养和数学运算素养等的好题．问题的思路开阔、解法多样、形式简单、结构优美，是一道值得探究的好试题．同时，该问题的解决思路，蕴含了丰富的数学思想，如对称思想、“配凑”思想、整体化思想、代换思想、平移变换思想等，是高中数学思想的瑰宝，是渗透数学思想方法的好问题．接下来，先对原问题的解法进行探究，然后从等差中项或等比中项的角度，对问题进行适当的引申．

2.问题探究

思路1：等差定义法

思路2：定向“配凑”法

思路3：整体“平移”法

分析：对比条件和结论的结构，可以发现，条件中以单个字母作为分母，这与结论的结构完全相同，而条件的分母都是“1”，待证明的结论中出现了轮换对称结构，考虑将分子全部变成“a+b+c”，再利用分数恒等变形，就可化为待证明的结构．

评注：思路1从等差数列等比中项的性出发，然后将待证明数列前后项相加，再利用等价代换，建立三个数之间的数量关系，进而证明结论．思路2利用条件和结论之间的差异性，从结论的结构出发，利用条件的结构来凑结论需要的结构，进而达到证明的目的．思路3是从整体的观点出发，巧妙的运用了“1”的特性、等式的恒等变形和等差数列具有平移变换不改变等差特性的特点．从本质上讲，思路3可视为思路2的优化．从思路3可以发现，条件和结论之间，相当于作了两次变换，从条件出发，先作“a+b+c”的数乘变换，在作“-1”的平移变换，但这两种变换，不会改变等差数列等差的特性，但是会改变原等差数列的公差，即为等差数列的结论依然成立．

3.问题引申

通过上述解答的分析过程，可以发现，关于等差中项的证明问题，较为简单．若已知数列为等差或等比数列，试问数列相邻三项的倒数有怎样的数量关系呢？接下来，将从等差中项和等比中项的视角，来研究数列相邻三项或相邻k项倒数之间的数量关系，得到如下的一些结论，希望对大家有所启发和帮助．

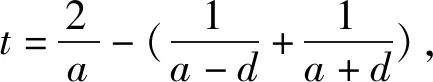
推广2 设数列{an}为正项等差数列，an=f(n)，公差为d，则当n≥2时，有：

推广3 设数列{an}为正项等差数列，an=f(n)，公差为d，对任意的正整数k，则当n≥2，且n-k≥1时，有：

推广4 设数列{an}为正项等比数列，an=f(n)，公比为q，则当n≥2时，有：

推广5 设数列{an}为正项等比数列，an=f(n)，公比为q，则当n≥2时，有：

推广6 设数列{an}为正项等比数列，an=f(n)，公比为q，对于任意正整数k，则当n≥2，且n-k≥1时，有：

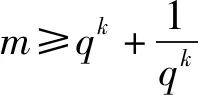
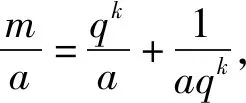
评注：推广1是从等差中项的角度，考察了等差数列相邻三项倒数之间的大小关系．推广2是从等差数列公差的角度出发，讨论了等差数列前后两项的倒数之和与等差中项倒数的公差倍数之间的关系，由此可以得出两个漂亮的不等式．推广3是对推广1的再推广，讨论了等差中项倒数与间隔k项倒数之和之间的大小关系．推广4-6，是对等比数列的等比中项的倒数与前后两项(或间隔k项)倒数大小关系的讨论，研究的范式与推广1-3是相同的，分别得出了等比中项的倒数与前后两项(或间隔k项)倒数之间的不等关系，此处不再作具体的分析．