一道三元分式函数值域问题的反思及推广
2021-11-10广州大学附属中学510006朱惊涛
中学数学研究(江西) 2021年10期
广州大学附属中学 (510006) 朱惊涛
广州大学数学与信息科学学院 (510006) 蔡 飘

该问题相当于求函数f(x,y,z)的值域,其标准答案如下:
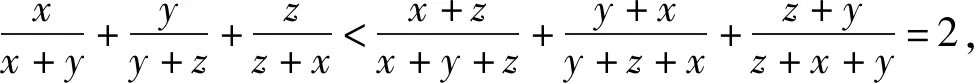
反思该答案,比较难以理解的是求极限过程中为何要令z=1,笔者经过分析发现,其实不一定要令z=1,令z等于任何一个常数都是可以的,其思想方法就是固定z,然后分别让x、y趋向两边,从而得到f(x,y,z)取值的一种极限状态.考虑到用降元法解决多元问题的数学思想,笔者给出该问题的另一种解法:

结论1 令min{a,b,c}表示a,b,c中的最小值,max{a+b,a+c,b+c}表示a+b,a+c,b+c中的最大值,则函数f(x,y,z)的值域为(min{a,b,c},max{a+b,a+c,b+c}).

①当t1→0,t2→0时,g(t1,t2)→a+b;
②当t1→+∞,t2→+∞时,g(t1,t2)→c;



⑥当t1→+∞,t2→0时,可令t1t2→0,此时g(t1,t2)→b;
⑦当t1→+∞,t2→0时,可令t1t2→+∞,此时g(t1,t2)→b+c;
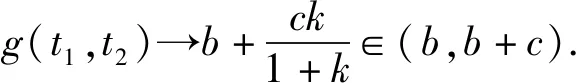



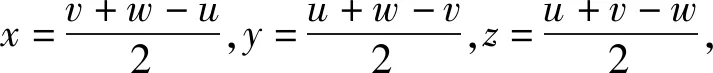

该结论还可以推广到n元的情形,即:


