Nesbitt不等式的一种新推广

江西省共青城市国科共青城实验学校 (332020) 姜坤崇 蔡立艳

这是一道简洁、经典、应用广泛的不等式，历史上曾作为1963年莫斯科数学竞赛题出现过，对它的研究(如证法，加强，推广，应用等)也历久不衰，本文给出它的一种新推广.

命题1 设a,b,c是正实数，k是整数，则

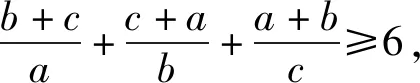
(ii)当k=0时，②式即3≥3,等号成立.

(iii)当k=1时，②式即为①式.

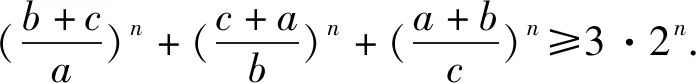
综上，命题1中的不等式得证.

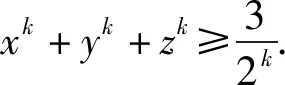
命题1中的不等式②是关于三个正数a,b,c的不等式，若将它推广为n(n≥3)个正数的不等式，则有如下命题3成立.证明从略.同样的，命题2中的不等式也可以推广到n(n≥3)个正数中去，有如下命题4成立.证明从略.

命题4 设xi>0(i=1,2,…,n,n≥3),且