一道2021年广东高三模考试题的探究

福建省莆田第一中学 (351100) 林 敏

1.试题再现

2.试题赏析

考题第(1)问考查了椭圆的定义和几何性质，可以利用待定系数法求椭圆的标准方程，第(2)问是椭圆的定值问题，涉及直线与椭圆的位置关系以及弦长公式，考查在解析问题中进行代数运算的能力和数学运算、逻辑推理和直观想象数学学科核心素养.该题不但着力考查了考生的综合思维能力、创新意识和数学素养，还留下很大的拓展空间.

3.解法探究和拓展探究

以下对这道试题进行解法探究和拓展探究.

评注：将已知点的坐标代入椭圆的方程，根据椭圆离心率的公式以及c2=a2-b2，建立关于a2和b2的方程组，解出a2和b2的值，从而得出椭圆C的标准方程.

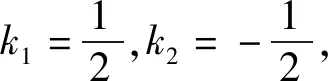
评注：先讨论直线MN斜率不存在时的情况，当直线MN斜率存在时，将直线MN方程和椭圆方程联立消元后，先求判别式，再由韦达定理表示两根之和与两根之积，再结合直线方程表示y1y2，由已知条件和直线斜率公式得出等式2t2=4k2+1，整体代换后得出△>0，由弦长公式和点到直线距离公式列式子，在运用整体代换法可得出△OMN的面积为定值1.

通过比较上面三种解法发现，解法1几何直观利用的较少而代数运算较多，体现了几何问题代数化和设而不求的思想方法，但其中代数运算运用较繁琐，解法2运用参数方程法，把解析几何中的面积定值问题化归为三角恒等变换问题，并且运算量减少，令人耳目一新，解法3运用了伸缩变化法，借助伸缩变换将椭圆中的问题化归为圆中的问题，几何直观增多而代数运算减少，但这种解法对学生的思维能力要求较高，只有考生非常熟练伸缩变换的性质的前提下该解法才会运用自如，否则容易出错.