基于桩锤激励的浅层孔洞智能探测技术

2021-11-10李浩祖陈敬松周立成刘泽佳刘逸平蒋震宇汤立群

土木工程与管理学报 2021年5期

李浩祖，陈敬松，周立成，刘泽佳，刘逸平，蒋震宇，汤立群

(1. 华南理工大学土木与交通学院，广东广州 510641； 2. 广州市高速公路有限公司，广东广州 510030；3. 广州广佛肇高速公路有限公司，广东广州 510289)

孔洞是指可溶性岩石在喀斯特作用下形成的地下空间，广泛存在于我国各个省市，尤其是西南地区。地下孔洞对基础工程施工的安全性造成严重威胁，在桩基施工扰动作用下可能发生坍塌，在灌注混凝土时也容易发生漏浆、塌孔等事故，从而造成经济损失甚至威胁施工人员的生命安全[1]。因此，发展高效的孔洞探测技术，可以为施工前期土层地质状况的评估提供可靠的技术保障，并为之后的施工方案提供指导，进而保证基础工程的施工安全。

目前，孔洞探测技术主要包括浅层地震波反射法[2～7]、高密度电阻率法[8～14]、钻孔雷达法[15]、管波测试法[16]等地质勘查手段。其中，地震波反射法通过在地表附近进行激震从而产生人工地震波，地震波传播过程中遇到不同岩性的界面时会发生反射，通过在地面捕获信号并对其进行分析从而推断出波的传播途径及其介质结构。该方法的优点在于勘探精度较高，方法简便，但是需要以炸药作为激震源，存在一定的风险。高密度电阻率法则是通过在地下施加人工电场流，通过观察地下传导电流的分布规律从而得到关于断面的分布。该方法的优点在于传感器布置简便，只需要一次布置好测点，仪器便可以自动采集数据，但是需要布置密集的测点。钻孔雷达法利用电磁波能在岩土中穿透的特性，利用一个天线发射高频宽带电磁波，另一个天线接收地下经岩石的波并进行分析，从而得到钻孔附近的地质情况。该方法的优点在于精度较高，缺点则是勘探范围较小，且价格昂贵。管波测试法与钻孔雷达法类似，通过观测管波物理场得到探测孔附近孔洞、裂隙等不良地质的分布。其优点在于精度高，勘探速度快，缺点是探测范围较小。综上所述，当前的孔洞探测技术仍然面临探测效率低、成本高、不易于大面积应用等瓶颈。

近年来，机器学习作为计算机科学的分支，备受各个专业领域学者和技术人员的广泛关注，并获得了迅猛的发展，出现了诸如决策树(Decision Tree，DT)、随机森林(Random Forest，RF)、k近邻算法(k-Nearest Neighbor, KNN)等经典的机器学习模型以及卷积神经网络(Convolutional Neural Network，CNN)和循环神经网络(Recurrent Neural Network，RNN)等深度学习算法[17]。由于其出色的运算能力、自我学习能力以及可避免人为误差等优势，机器学习被广泛应用于人脸识别[18]、文字识别[19]和生物学[20]等领域。在地质勘探领域，国内外学者对基于机器学习的高密度电阻率法已有了一些研究。El-Qady等[10]进行了神经网络电阻率二维反演的初步研究；徐海浪等[11]利用BP(Back Propagation)神经网络优化方法对数据进行电阻率二维非线性法反演，实现对埋深5 m的高阻与低阻异常体进行定位，且比传统线性化的迭代反演结果更好；赵涛等[12]则借助GA(Genetic Algorithms)-BP神经网络算法实现了高密度电法非线性反演，发现遗传算法(GA)可对BP神经网络的权值与阈值进行优化，提高全局的寻优性。然而，由于数据来源于高密度电阻率法，因此仍然不能避免其勘探面积较少和传感器需要密集布置等缺点。此外，亦有部分学者基于机器学习实现地震波反射法的地质探测。Di等[7]基于地震数据，通过对比卷积神经网络与多层感知机在识别盐体与断层时发现，卷积神经网络的效果明显优于多层感知机；林年添等[21]通过卷积神经网络，利用有限的已知井段信息构建卷积核，从而识别出该地区的地震油气特征，通过少量样本便可实现全局识别，大幅度缩减了检测时间；此外，任海洋[22]利用卷积神经网络与深度回归森林实现了在二维情况下孔洞体的识别及其体积定量预测。然而，以上方法的数据仍然需要通过传统的地震波反射法来进行采集，传感器布置较多，勘探成本较高，需要危险的激励源，且都是基于二维条件下的勘探。本文旨在探索一种高安全性、高效率和低成本的智能孔洞探测技术。一方面，借鉴浅层地震波反射法的原理，以基础施工过程中的桩锤激震代替炸药作为激励源，并通过少量的加速度传感器测量地表的孔洞反射信号，用以预测孔洞的位置和尺寸，从而在提高安全性的基础上降低探测成本；另一方面，通过有限元模拟获得大量工况下的响应数据，利用应力波原理提取地表加速度时程数据的内在特征，并以此人工特征作为输入建立机器学习模型，从而实现高效率和低成本的孔洞探测技术。

1 浅层孔洞智能探测技术总体方案

如图1所示，本文所提出的孔洞探测方案为基于桩锤激震的智能探测技术，借鉴现有的浅层地震波反射法，用桩锤锤击土层的激励代替传统方案中的炸药激励，通过观察桩锤激震后产生的地震波对地表特定位置加速度响应的影响规律，并建立机器学习模型，判断土层中是否存在孔洞，并实现对孔洞位置和大小的预测。其具体步骤如下：

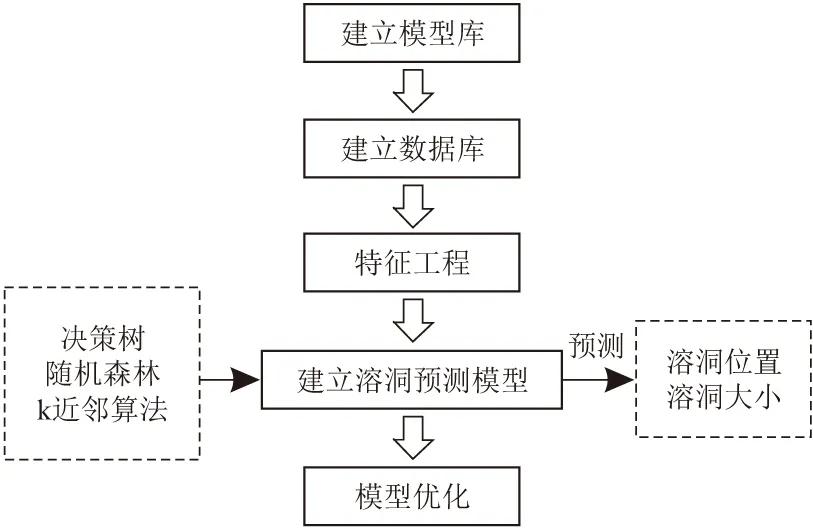
图1 基于机器学习的孔洞识别方法

(1)建立包含不同位置和大小的孔洞模型库，用于计算不同工况下的响应数据集，为机器学习模型的训练和预测提供数据源；

(2)利用有限元软件模拟桩锤激震下不同工况(孔洞位置和大小)的地表特定位置加速度响应时程信号，形成原始数据集；

(3)通过对加速度响应数据的规律进行分析，提取相应的数据内在特征，并将特征与标签(孔洞位置和大小)组合成数据库，进一步对机器学习模型进行训练和优化，获得最优的孔洞预测模型。

传统的浅层地震波反射法通常以炸药作为激励源，其安全性与易用性不足，本文所提出的方法以施工过程的桩锤激震代替危险的激励源，相比之下具有更好的安全性，并且降低了成本。再者，在传统方法中对孔洞的预测往往涉及大量数据处理过程，需要丰富的领域知识或专家经验，数据分析的效率和成本较高，而本文基于机器学习建立的孔洞预测方法，提供了一种无需过量人工干预和领域知识的探测方法，提高了数据分析的效率，并且有利于技术的推广和应用。

2 模型库

在实际工程中，地下孔洞大小不一、形状各异，且土层性能千差万别，加之周围环境错综复杂，地表加速度响应不仅受到地下孔洞的影响，还包含了诸多干扰因素的共同作用，这给数据分析带来了极大的挑战。本文旨在探索机器学习用于地下孔洞探测的可行性，因此在建模中将对问题进行简化。为了获得用于机器学习训练和性能评价的数据集，首先需要利用有限元软件建立包含不同孔洞位置和大小的模型库；其次，通过有限元计算获得不同工况下地表特定位置加速度响应的时程信号；最后，通过特征工程提取对孔洞位置和大小具有敏感性的内部特征，并将这些内部特征(作为机器学习的输入)和孔洞的位置及大小(作为机器学习的输出)一一对应组成样本，形成数据集。

2.1 模型参数

由于机器学习需要成千上万的数据量作为训练集和测试集，而实测数据的成本过高，且工况复杂，因此本方法将借助有限元仿真来建立简化的模型库并获取数据集。如图2所示，土层用尺寸为30 m×30 m×30 m的立方体进行模拟，并假定每一种工况只有一个孔洞，且孔洞的几何形状为球形。土层的本构模型采用经典的Mohr-Coulomb本构模型[23]，其本构参数如表1所示。值得注意的是，在实际工程应用过程中需要根据实测数据对土层的本构参数进行修正，从而获得更符合实际情况的有限元模型，以便为机器学习模型提供更准确的数据集。

图2 有限元模型及传感器布置方案示意

表1 土层本构参数

桩锤模型采用直径为1.5 m、高度为0.75 m的钢块进行模拟，其总重量为4 t。桩锤从距离地表1 m的高度自由下落锤击土层，从而产生应力波，并经过孔洞与土层界面产生反射波。此外，为了保证脉冲激励作用下响应时程信号的完整性，本方案采用的采样时间为0.3 s，步长为1 ms。

边界条件是影响有限元模型准确性的关键因素之一。为了模拟应力波在半无限空间土层中的传播特性，传统的解决思路是建立一个尺寸足够大的模型以防止地震波的反射。然而，这种方式容易导致模型尺寸过大、计算成本过高的问题。为了缩减模型尺寸、并尽可能减少地震波在边界的反射，本文采用无限单元的形式设定边界条件[24]。运用Abaqus有限元软件进行建模，可在软件内置的17种无限单元类型中选择CIN3D8单元来定义土层模型的无限边界，内部的单位则为有限元单元C3D10M，有限元与无限元边界处单元为C3D8R，以实现无限元与有限元界面的耦合，最终模型的有限元网格大约为70万。

虚拟加速度传感器的布置方案采用如图2所示的两种方案，在土层表面上距激震中心一定半径的圆圈上对称布置4个或者6个传感器，以用于获取地表的加速度信号。如图3所示，当传感器布置范围过大为15 m时，传感器采集到的加速度信号变弱、易受噪声干扰，从而降低了精度；而当传感器布置范围过小为5 m时，虽然信号较强，但探测面积过小，降低了效率。经过计算分析，最终将传感器的布置半径确定为10 m即可平衡上述矛盾。

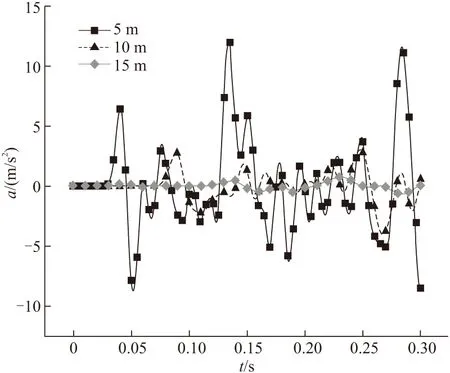
图3 不同位置采样点下的加速度响应信号

2.2 模型数量缩减

在确定模型的基本参数后，需建立各种工况下(不同孔洞位置和大小)的批量模型库，以用于后续的有限元计算。如图4所示，本文假设每一个模型中仅有一个孔洞，且其几何形状为球形，孔洞球心到激振源垂线的距离L有6种情况：0，2，4，6，8，10 m；孔洞顶部到地表的垂直距离H有7种情况：2，3，4，5，6，7，8 m；孔洞的方位角θ有72种情况，即每5°建立一个工况；孔洞直径D有3种情况：4，6，8 m。因此，模型的数量一共为5832个。

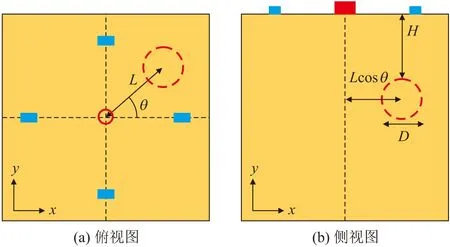
图4 孔洞位置与大小

如果单个模型的计算时间约为2 h，针对以上模型的计算需要耗费约1万h。为了缩短建立有限元数据库的计算时间，本文采用如下方案实现模型数量的缩减。由图2的传感器布设方案可知，单个模型(工况)只需要对其中的4个点或者6个点进行加速度数据的存储。根据对称性，可以通过旋转传感器分布角度的方式，来获得不同孔洞位置下的地表响应。因此，可以通过在一个确定的工况下布设更密集的传感器，来等效获得不同工况(孔洞方位角)下以4个或者6个传感器为一组的数据集。如图5所示，以4个传感器布设方案的模型为例，在某一个工况下，在半径为10 m的圆周上每5°布置一个虚拟传感器用以存储加速度响应，在单次时程分析过程中，即采集了72个位置点的加速度信号。以4个沿着圆周均匀布设的传感器为一组组成数据集，则单次有限元时程分析等效地包含了72种工况(孔洞方位角)。因此，模型数量可以缩小72倍，从而极大地提高了计算效率。本文中，四测点与六测点下的计算模型数量由5832个均缩减为81个，总工况数皆包含5832个。

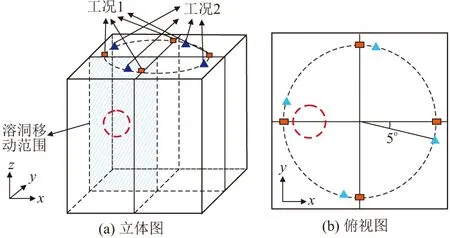
图5 缩减模型数量策略示意

3 数据分析与特征工程

机器学习方法主要分为监督式学习与非监督式学习，经典的监督式学习方法主要有决策树模型、随机森林、支持向量机和神经网络等算法。相对于具有自动学习数据层次特征的深度学习算法而言，浅层的机器学习算法的性能高度依赖于特征工程。本文将首先探索浅层机器学习算法在孔洞探测中的适用性和有效性，因此需要对加速度信号进行分析，以便于提取对孔洞位置和大小具有高度敏感性的内在特征，从而提高预测模型的性能。

为了研究孔洞位置对加速度信号的影响规律，考察孔洞处于激震源正下方时不同埋深H对土层表面加速度响应的影响规律(图6)。从图6可以看出，当只改变孔洞埋深H时，第一个波峰的峰值和出现的时间不产生变化，即与孔洞位置无关，可以推测该波峰是地震波纵波沿着表面土层传播到传感器位置处而产生的；加速度时程曲线上的第二波峰的峰值和出现的时间有明显的变化，且可以清晰地看出随着孔洞埋深增大，第二峰值响应出现的时间则越晚，因此可以推测该波峰是纵波在土体内传播并经孔洞反射后传播到地表的响应。

图6 孔洞深度对地表加速度响应的影响

为了验证第二波峰产生的原因，可以使用理论公式对应力波的走时进行估计。纵波波速vp为：

(1)

式中：E为弹性模量；v为泊松比；ρ为密度。将表1中的本构参数代入上式后，可得到纵波的波速vp=112.69 m/s。

如图7所示，以直径为6 m的孔洞为例，采用最短反射路径对反射波的走时进行计算。表2展示了从任意一个数据采集点处获得的第二峰值所对应的时间与理论计算时间的对比结果，可以观察到两者基本吻合。因此可以证明该波峰为纵波经孔洞反射后到达地表所产生的响应。鉴于此，可以将第二波峰所对应的时间与峰值作为机器学习的特征。

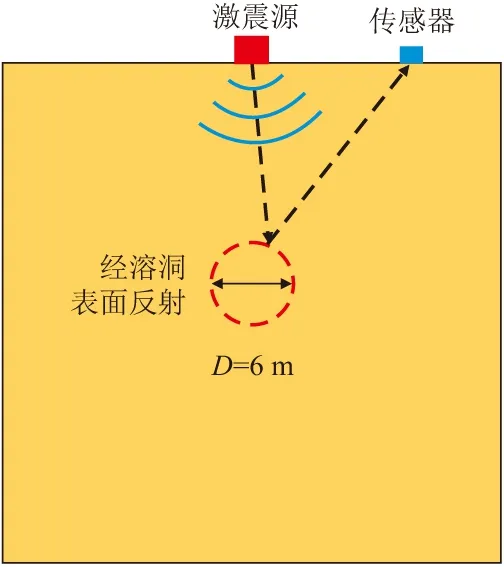
图7 反射波的传播路径

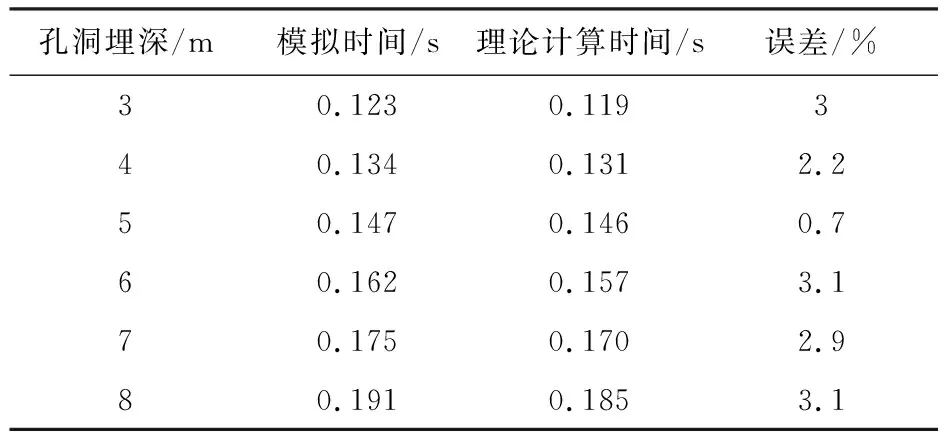
表2 有限元和理论计算结果对比

由于不同土质之间本构的最大区别为杨氏模量的大小。而弹性模量对地表加速度时程曲线影响最明显的便是特征时间及其峰值。因此本文将只建立单一本构下的模型库。

同时，如图6所示，当孔洞处于较浅位置时，地震波经孔洞反射后传播到地表的响应时间较早，从而影响了第一波谷出现的时间和峰值。因此，该波谷所对应的时间及峰值也可作为机器学习模型的特征。综上所述，本文将如图8所示的第一波谷的峰值amin及其对应的时间tmin、第二波峰的峰值amax及其对应的时间tmax作为特征，以此不增加额外领域知识的情况下探索机器学习用于孔洞预测的可行性和有效性。

图8 特征工程(H=4 m,D=6 m)

4 传统算法的局限性

本小节将利用传统算法来验证所提取的特征用于预测孔洞位置和大小的可行性，并检验传统算法的精度和鲁棒性，从而说明引入机器学习算法的必要性。借鉴传统的浅层地震波反射波法根据纵波反射时间来界定断层位置的原理，本节将以反射时间作为已知条件，并利用拉格朗日法来预测孔洞的位置和大小。

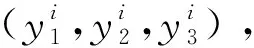
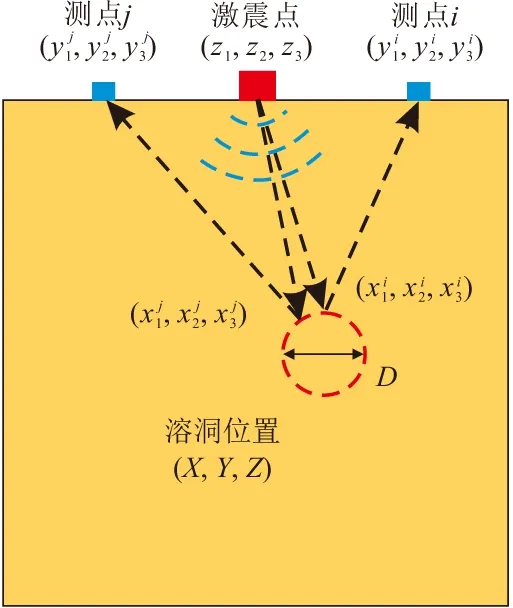
图9 地震波反射法原理

(2)

式中：i=1，2，…，6。然而，仿真数据上的第二波峰时间与实际上纵波波前到达地表的时间会存在一定的误差，这会导致推算出来的反射点与理论上孔洞表面的反射点之间存在偏差。因此，本文将使用方差最小化来获得最优解，即通过计算基于数值仿真得到的反射波时间估计的路径长度与实际反射路径长度的方差和的最小值来判断结果是否为最优解，因此引入方差函数l：

(3)

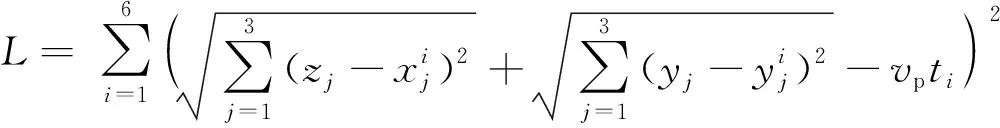
(4)

随机选取几个算例进行计算，得到如表3所示的结果。可以看出，该方法所得到的孔洞定位偏差较大，而且容易将孔洞的直径预测为0。这是因为基于数值方法的预测精度很大程度上依赖于纵波反射到地表的时间tmax的精度。而由于纵波在土层是以球形波的形式进行传播的，因此到达地表的加速度信号所对应的时间不一定就是波前到达地表的时间。而且纵波在表面土层传播速度较快，因此0.01 s的时间误差就会导致1 m的路程误差。这对于球形孔洞的定量与定位会产生极大的影响。此外基于数值方法的孔洞预测模型是孤立的，并没有与其他的工况相关联，因此其抗噪性能很差，从而极大降低了孔洞的预测精度。因此，为了解决这一问题，本文将引入机器学习算法来建立孔洞识别模型。

表3 孔洞位置和直径的实际值与计算值对比

5 机器学习原理

作为计算机科学的分支，人工智能在近几十年发展十分迅速，并衍生出了很多性能优异的算法。本文将采用决策树、随机森林与KNN算法建立孔洞预测模型。

5.1 决策树

回归决策树是一种基于Classification and Regression Tree (CART)算法的决策树，它的基本构造是二叉树，即在每次分支的时候，二叉树会基于特征将训练集划分成两部分。对于回归问题，CART算法采用的是平均误差最小化 (Mean Squared Error，MSE)作为最佳特征选择的准则。如图10所示，假设m与n分别为输入与输出变量，其中n为连续变量，训练集d如式(5)所示：

图10 CART回归树原理

d={(m1,n1),(m2,n2),…,(mN,nN)}

(5)

在确定训练集之后，回归树首先需要从特征中选取最优特征来对训练集进行划分。通过遍历所有特征以及特征对应的切割点s并最小化均方误差，从而得到最佳的第j个特征m(j)以及其最佳的切割点s。随后基于上述的j和s将数据集分割为两个区域，如式(6)所示。

(6)

在下一个分支点时重复上述的操作，直到满足停止条件为止，即构成一棵基于CART算法的回归树。

5.2 随机森林

随机森林是指利用多棵决策树对样本进行训练并预测的算法，它的输出是由个别决策树的输出决定的。如图11所示，假定训练数据中共有N个样本的训练集与k个特征，构造一棵决策树需要在样本库中随机且有放回地抽取N个样本作为子训练集并生成决策树，随后随机从k个属性中选取m个作为该决策树分枝的依据。基于上述方法建立i棵决策树，最终预测结果也是基于每棵决策树预测结果的平均值从而得到最终预测结果。随机森林算法的优点在于有很强的抗过拟合能力，而且结果较稳定。

图11 随机森林

5.3 KNN算法

如图12所示，邻算法最核心的思想是将所预测的样本用距离它最接近的k个邻居来表示，而在回归问题上则通过对这些邻居的属性进行平均或者加权而获得。图中不同形状代表不同类别的样本。通常邻算法中的距离可用欧氏距离dxy进行度量：

图12 KNN算法

(7)

式中：xk，yk分别为训练集x与测试集y的特征向量。计算步骤如下：

(1)计算训练集数据点到当前点的距离；

(2)按照距离依次递增排序；

(3)选取与当前点距离最小的k各点；

(4)对k个点加权平均或取平均，确定输出值。

KNN算法的优点也十分显著，容易理解，精度高，理论成熟，且对异常值不敏感。

6 基于机器学习的孔洞预测模型

6.1 特征组合

本文将采用决策树模型、随机森林、KNN算法来建立孔洞探测模型，特征(输入)将选取如表4所示的五种组合进行研究。

表4 特征组合

6.2 容许误差和性能指标

由于孔洞定位与定量模型使用的是回归模型，预测值几乎不可能恰好等于实际值，且工程实际问题允许预测值与实际值存在一定的误差，因此引入容许误差。

假设预测出来的孔洞位置坐标为(Xp,Yp,Zp)，孔洞直径为Dp，而孔洞的实际位置为(Xr,Yr,Zr)，孔洞实际直径为Dr，容许误差为r，当满足式(8)时，即可认为预测值是准确的。

(8)

为了评价孔洞预测模型的性能，本文将用精确率来对其进行判断。假定在测试集中预测准确的工况数为Nc，测试集总工况数为Ntotal，则精确率acc为：

acc=Nc/Ntotal

(9)

6.3 模型训练

在输入特征组合、机器学习方法与容许误差确定之后，便可进行机器学习模型的训练。在本文中，数据集将以4∶1的比例随机分为训练集与测试集，其中训练集包含4665个样本，测试集包含1167个样本。机器学习算法在训练过程中需要进行超参数的调节以优化模型。其中，决策树主要需要调节叶子节点最少的样本数与树的最大深度，在进行参数调节后叶子节点最少的样本数确定为20，树的最大深度为10；随机森林主要调节的参数为最大决策树个数，采用默认值100，决策树单元的参数参考上述决策树算法的参数进行设置；KNN算法则是k值，默认为5。确定超参数之后，便可对上述模型进行训练。

表5展示了上述三种方法在六测点情况下，分别以五种特征组合作为输入、以孔洞顶端坐标及其直径作为输出时训练集与测试集的拟合优度。从表5可以看出，各方法训练集与测试集拟合优度之间的差别不大，因此我们可以认为所建立的模型不存在欠拟合和过拟合的情况。

表5 六测点模型下各机器学习算法训练集与测试集拟合优度

6.4 孔洞定位

本小节将首先对孔洞位置进行预测，即输出中不包含孔洞的直径。基于决策树、随机森林与KNN算法，分别采用如表4所示的五种特征值组合进行机器学习，实现孔洞探测，并采用式(9)所示的精确率进行算法的性能评价。

表6为四测点方案下各机器学习算法孔洞定位的精确率。在上述五种特征组合中，以组合A与组合B为输入建立的孔洞位置预测模型的精确率明显高于其他三种特征组合，而以组合C为输入建立的模型精确率最低。这是因为特征组合A与B都包含与孔洞位置相关性最大的特征amax和tmax，而组合C仅仅由与孔洞位置相关性最弱的amin和tmin组成。同时，由组合E的效果优于组合D的现象可以推断出特征tmax与孔洞位置的相关性高于特征amax。此外，在算法方面，KNN算法的定位精确率优于决策树、随机森林模型的精确率。事实上，决策树与随机森林将数据分成多个叶结点，随后通过对叶结点内的样本求平均获得预测值。在调参的过程中发现叶结点的最少样本数为20才能获得较好的性能，这就导致了所得到的结果是由与该被测试样本最接近的20个样本的均值决定。而KNN算法的输出则是由最接近的5个样本来确定，因此相比于决策树与随机森林的结果会更加准确、拟合程度更好。从表6可以看出，在四测点方案中，当容许误差为2 m时，以特征组合A为输入的KNN算法具有最高的定位精确率(94.3%)。

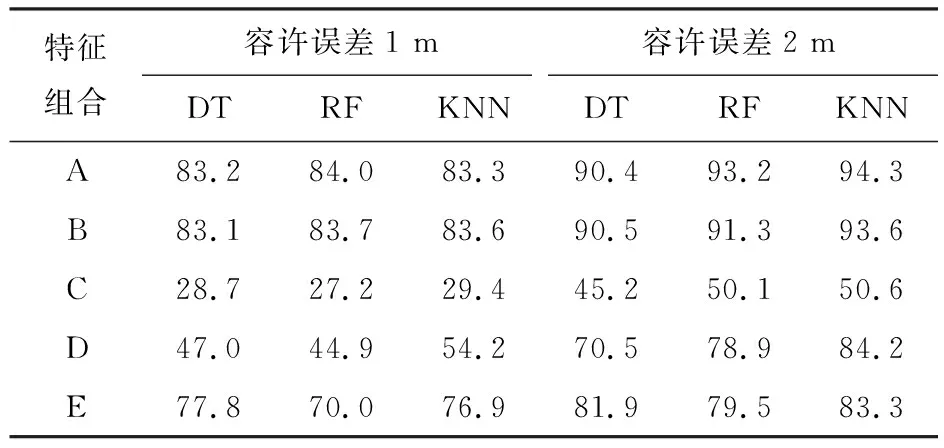
表6 四测点方案下各机器学习算法孔洞定位的精确率 %

表7则是六测点方案下各机器学习算法孔洞定位的精确率。与上述结果类似，最佳的特征组合也是组合A与组合B，预测精确率最低的是组合C。而最佳算法依然是KNN算法，且当容许误差为2 m时，以特征组合A为输入的KNN算法具有最高的定位精确率(98.3%)。

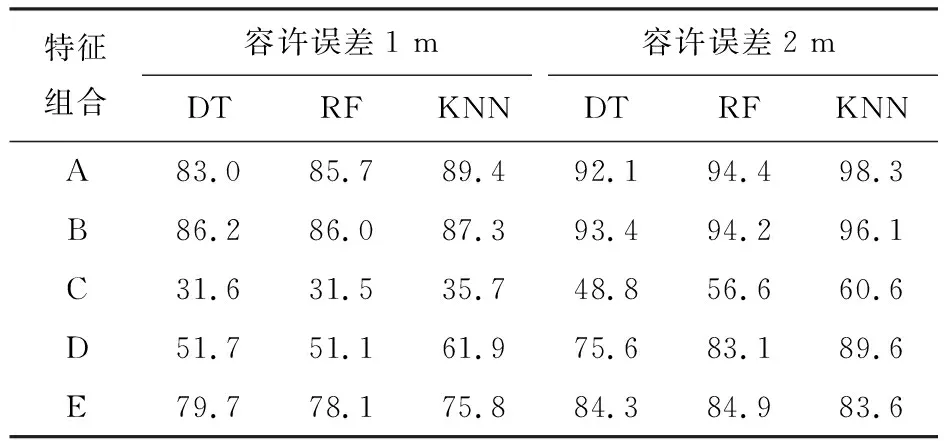
表7 六测点方案下各机器学习算法孔洞定位的精确率 %

对比表6，7可以发现，基于六测点模型的精确率几乎都高于四测点的孔洞定位模型。这是因为六测点方案中输入的信息多于四测点方案，更有利于对孔洞位置的预测。同时可以发现，当选择特征组合A或B时，六测点模型仅稍优于四测点模型，这说明恰当的特征选择有利于减少传感器的数量，从而降低探测成本。综上所述，六测点方案下以特征组合A作为输入的KNN算法具有最高的定位精确率。

考虑到实际工程现场的测试环境复杂、干扰因素繁多，因此建议在实际应用中采用至少六个测点的测量方案，以提高方法的准确性。

6.5 孔洞定位与定量

本小节将同时对孔洞顶部位置与直径进行预测。由于六测点布置方案优于四侧点方案，因此接下来将基于六测点的传感器布置方案同时对孔洞进行定位与定量识别。

表8为机器学习算法同时预测孔洞位置和直径的精确率。对比表7的结果可以看出，同时进行孔洞位置与直径的预测精确率相对于单独进行孔洞位置预测的精确率都有所降低。这是因为需要输出的变量增多之后，预测值更难以匹配实际值。尽管如此，KNN算法依然表现优异：以特征组合A作为输入时，容许误差为1 m的情况下精确率有82.0%；容许误差为2 m的情况下精确率可达97.6%。

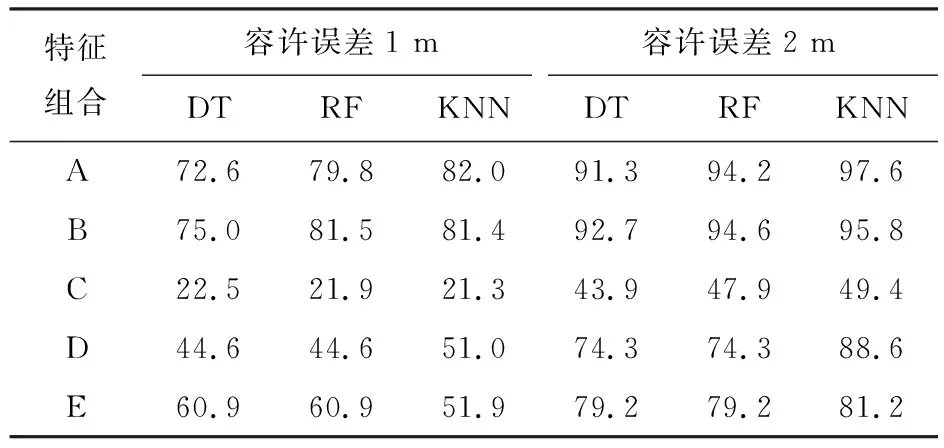
表8 机器学习算法孔洞位置和直径的精确率 %

6.6 KNN算法孔洞识别模型优化

最后，在六测点布置方案下，以所有特征的组合A作为输入的KNN算法模型进行优化。当k值过小时，模型会出现过拟合现象；当k值过大时，模型则会有可能出现欠拟合现象。因此，优化的过程主要通过调节参数k实现。图13展示了k值从1～15的情况下模型预测精确率的变化。可以看出，在容许误差为1 m的情况下，随着k值的增大，孔洞定位与定量模型的预测精确率先出现上下波动，随后当k值大于6时，精确率开始单调下降。当k值为2时，算法的精确率最高，为88.6%。当容许误差为2 m时，随着k值增加，孔洞定位与定量的预测精确率在逐渐降低，但是变化较小。当k值为1时，容许范围为2 m的预测精确率最高，为98.1%。综上所述，可采用k=2作为最佳的参数来建立孔洞定位与定量预测模型。