附设粘滞阻尼器的高层立体车库风振性能
2021-11-10邹平波陈繁荣
邹平波, 陈繁荣, 沈 琪, 赵 强, 李 英
(1.中国联合工程有限公司, 浙江 杭州 310052; 2. 中南建筑设计院股份有限公司, 湖北 武汉 430071)
立体车库是一种新的城市停车形式[1],高层立体车库不同于一般高层钢结构,其内部没有刚性楼板,在沿海地区,风荷载对于高层立体结构影响较大,容易产生较大的风振响应,附设粘滞阻尼器可以减少结构吸收风荷载能量,减小高层立体车库的层间位移和内力。对于高层立体车库和阻尼器减振技术,许多学者进行了研究。贺拥军等[2]通过将水平阻尼支撑应用于立体车库,通过地震作用下的动力时程分析,确定了最优阻尼支撑参数。周云等[3]在框剪结构隔震层中设置变性能粘滞阻尼器控制结构的地震响应和风振响应,证明了变性能粘滞阻尼器有良好的减振限位效果,工程价值良好。陶义等[4]在立体车库中设置摩擦阻尼支撑,在地震作用下分析了摩擦耗能支撑的刚度和滑动摩擦力对结构响应的影响,获得了摩擦耗能支撑的优化参数。
目前对高层立体车库的抗风设计研究较少;计算风荷载响应时,设计人员一般将风荷载等效为静荷载,没有考虑脉动风的动力特性;在附加阻尼器至结构时,很多研究没有排除阻尼器自身刚度对结构自振特性的影响。基于以上几点,本文通过数值模拟方法生成总风压时程函数,仅引入附加阻尼至结构,以减振率和风振吸收能量为风振性能指标,对改进后的高层立体车库的抗风性能进行了探讨。
1 结构计算模型
1.1 原结构有限元模型
高层立体车库采用钢框架结构,x向隔层布置十字形支撑,y向隔层布置人字形支撑,结构平面图和立面图如图1,2所示。结构首层层高取2.5 m,其他层层高取2.2 m,结构层数20层,总高度为44.3 m。梁柱节点按刚接处理,柱底简化为固接,柱截面型号为H300×200×8×10,x向框架梁型号为H250×150×6×8,y向框架梁型号为H200×150×6×8,结构支撑截面型号为φ95×5,钢材采用Q235B。结构为了考虑车辆和电梯荷载,在每个梁柱节点施加800 kg的集中质量[5]。本文采用ANSYS软件进行计算分析,材料的本构模型采用双线性随动强化模型,切线模量为1100 MPa。梁柱采用BEAM188单元,支撑采用LINK8单元,梁柱结点处的集中质量采用MASS21单元。

图1 立体车库结构平面/mm
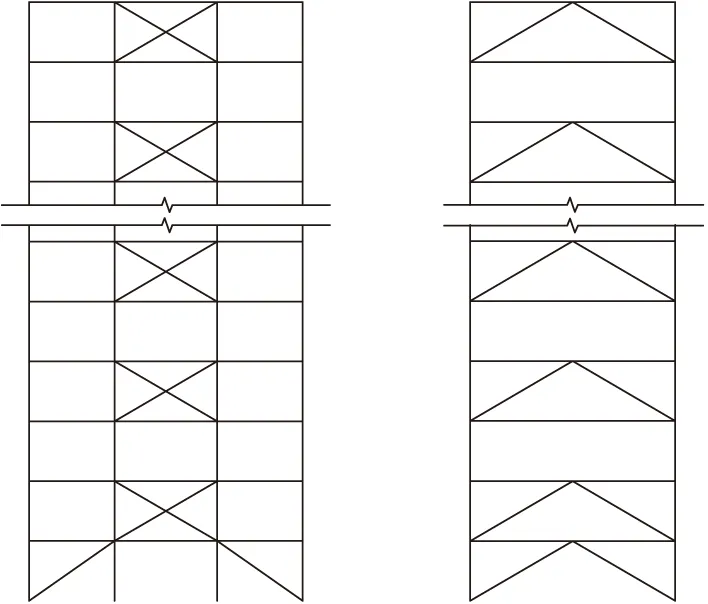
图2 立体车库结构立面
1.2 粘滞阻尼器力学模型
传统的结构减振技术主要依赖结构自身刚度以“硬抗”方式抵抗风荷载,但是随着结构自身刚度的增加,结构吸收的风振能量也会随之增加,对结构不利。所以附加阻尼器是控制结构风振响应的有效方法[6~9]。本文采用的粘滞阻尼器是经过粘弹性阻尼器改装的速度型阻尼器,通过附加阻尼控制结构响应,从而减少结构吸收的风振能量。本文对开尔文模型的粘弹性阻尼器加以改进,阻尼器的力学模型如图3所示,在ANSYS软件中用弹簧-阻尼单元COMBIN14进行模拟[10],计算时将COMBIN14单元的刚度常数Kd设置为0,形成粘滞阻尼器,从而结构的自振特性不会改变,仅附加阻尼起作用,则粘滞阻尼器的阻尼力fd的计算公式为:

图3 阻尼器力学模型
fd=Cdud
(1)
式中:Cd为阻尼常数;ud为阻尼器两端的相对位移。
粘滞阻尼器引入的附加阻尼比与阻尼常数关系密切,根据文献[11],选取阻尼常数Cd=1.5×108N·s/m。为了验证结构附加阻尼器之后,自振特性不变,对原结构和附设阻尼器结构进行模态分析,结构前两阶自振周期分别为1.458,1.269 s,前后没有发生变化。
2 风压时程函数
AIT Maatallah等[12]通过将Hammerstein模型改编为自回归模型,得到新的Hammerstein模型可以更好地捕捉各种风速特征。要进行风振时程分析,首先须确定总风压时程函数。总风压时程函数wt由两部分组成:
wt=wa+wp
(2)
式中:wa,wp分别为平均风压和脉动风压。
平均风压可以通过基本风压反算得到,脉动风压时程函数的获取有实测和人工模拟[13,14]两种方法。实测受外界条件干扰较大,记录结果有较大误差。人工模拟基于大量实测数据,分析数据的统计特性,获得满足条件的脉动风压时程。本文采用人工模拟获得风压时程数据,脉动风的功率谱Davenport谱[15]的经验公式为:
(3)
式中:n为脉动风速频率;x=1200n/v10av;Sv(n)为风速功率谱;K为地面粗糙度系数;v10av为标准高度的平均风速。
基于以上风速功率谱,本文通过风荷载时程处理程序WINDHIST V2.0获得风压时程函数[15]。该程序平稳随机过程的输出方法采用线性滤波法中的自回归模型(Auto Regressive Model,AR模型),程序中平均风压模型采用GB 50009-2012《建筑结构荷载规范》[16]的指数模型。分析过程中基本风压取0.45 kN/m2,地面粗糙度类别取B类,时间取10 min,结构顶部的总风压时程曲线如图4所示。获得结构不同楼层高度的总风压时程后,将楼层高度处的总风压乘以上下层层高的平均值得到沿楼层边梁分布的线荷载,将线荷载施加到楼层边梁上,形成结构的风荷载工况。

图4 结构顶部总风压时程函数
3 结构计算分析
3.1 结构风振性能指标
本文选取结构减振率和风振吸收能量作为风振性能分析指标,结构减振率ε定义为:
(4)
式中:θ1为附加阻尼器之后结构的最大层间位移角;θ0为原结构最大层间位移角。
结构的风振吸收能量为风荷载在结构位移中所作的功,结构的楼层位移取结构该层所有框架柱位移的平均值,结构某楼层在t时刻的风振吸收能量E(t)为:
(5)
式中:wt(t)为某楼层t时刻的总风压;A为某楼层总风压的受力面积;u(t)为某楼层t时刻的楼层位移。
结构的风振吸收能量为所有楼层的风振吸收能量叠加。
3.2 结构全高隔层布置阻尼器
本文采用两类阻尼器布置方案,分别为A类和B类方案,A类方案考虑在结构全高范围内隔层布置阻尼器,考虑四种布置形式,每层布置4个阻尼器,每种方案共36个阻尼器,阻尼器从结构第3层开始隔层布置,A类方案的四种阻尼器布置形式编号为A-1~A-4,如图5所示。方案A-1的阻尼器两端分别与梁柱节点和梁跨中相连,方案A-2的阻尼器两端分别与梁柱节点和梁1/4处相连,方案A-3的阻尼器两端分别与柱中部和梁跨中相连,方案A-4的阻尼器两端分别与柱中部和梁1/4处相连。B类方案考虑在结构局部层数布置阻尼器,阻尼器布置形式将在3.3节中进行讨论。
3.2.1 减振率
由于立体车库没有楼板,楼板的刚性假定并不适用于立体车库,所以立体车库在楼层平面内的变形不一致,故在风荷载作用下,立体车库的角柱变形和中柱变形不一样,由于中柱的抗侧刚度大于角柱,所以层间位移较角柱小,由于两根角柱之间设置人字形支撑,所以角柱变形时可以通过人字形支撑进行位移协调,角柱顶部位移较中柱小。4种阻尼器布置形式的减振率如表1所示,以中柱最大层间位移角为例,结构中柱最大层间位移角、结构顶部位移和风振加速度分别如图6~8所示。

表1 四种阻尼器布置方案的减振率

图6 中柱最大层间位移角

图7 最大顶部位移

图8 最大顶部加速度
通过以上图表可知,附设阻尼器之后,结构最大层间位移角得到了明显改善,其中方案A-1的减振效果最佳,中柱和角柱的减振率分别为29.2%,36.1%。且方案A-1的最大顶部位移和最大顶部加速度最小,中柱和角柱最大顶部位移分别为91.7,84.9mm,最大顶部加速度分别为100,83.5 cm/s2,四种布置形式的最大层间位移角、最大顶部位移和最大顶部加速度较原结构得到明显改善,但减振效果没有方案A-1明显。其中方案A-3在这四种布置形式中减振效果略差,方案A-2和A-3次之,所以在A类方案的四种阻尼器布置形式中,方案A-1最合适。
3.2.2 风振吸收能量
根据式(4)及ANSYS的分析结果计算最大风振吸收能量和阻尼器吸收能量,两者之差为其他构件吸收能量,如表2所示。
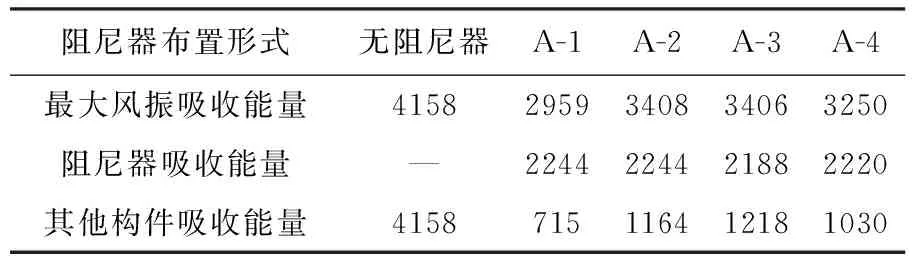
表2 四种阻尼器布置方案的风振吸收能量 J
结构的最大风振吸收能量和其他构件吸收能量明显减少,其中方案A-1的最大风振吸收量和其他构件吸收能量最少,分别为2959,715 J。四种布置形式阻尼器吸收的能量差别不大,所以在受力过程中,阻尼器主要是通过限制结构的位移减少结构吸收风振能量,结构吸收的风振能量越少,在阻尼器吸收能量相同的情况下,给结构梁、柱等其他构件带来的负担就会明显减少。所以从吸收风振能量角度考虑,方案A-1的布置显得更为合理。
3.3 部分层数隔层布置阻尼器
3.3.1 减振率
为了减少阻尼器的布置数量,考虑竖向布置位置的不同,引入B类阻尼器布置方案,将阻尼器布置形式分为底部布置、中部布置和顶部布置三种布置形式,每层布置4个阻尼器,每种方案共20个阻尼器,底部布置在结构第3,5,7,9,11层隔层布置阻尼器,中部布置在结构的第7,9,11,13,15层处布置阻尼器,顶部布置在结构的第11,13,15,17,19层布置阻尼器。根据3.2节的分析结果,阻尼器楼层布置形式按方案A-1效果最好,所以此处的底部布置、中部布置和顶部布置的楼层阻尼器布置形式参考方案A-1进行布置,三种布置形式编号分别为B-1,B-2,B-3,阻尼器布置如图5所示。三种阻尼器布置方式的风振响应如表3、图9~11所示。

表3 三种阻尼器布置方案的减振率

图9 中柱最大层间位移角
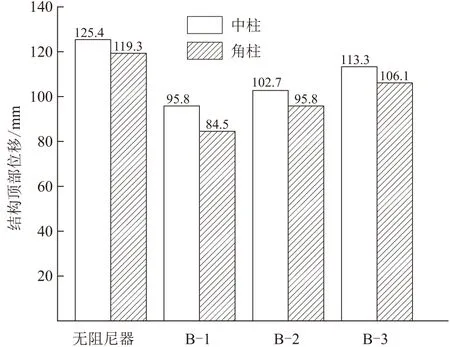
图10 最大顶部位移
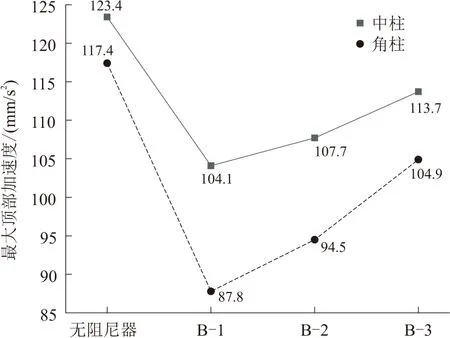
图11 最大顶部加速度
由图表可知,方案B-1的减振率优于方案B-2和B-3,同时方案B-1的最大顶部位移和顶部加速的控制效果最为明显,方案B-1中柱和角柱的最大顶部位移分别为95.8,84.5 mm,最大顶部加速度分别为104.1,87.8 cm/s2,方案B-2和方案B-3减振率比较小,两种布置方式中中柱的减振率分别为8.9%,1.1%,角柱的减振率分别为1.4%和0,但是这两种阻尼器布置方式可以改善结构顶部位移和顶部加速度。所以在三种部分层数布置阻尼器方案中,优先选择方案B-1。
方案B-1的中柱最大层间位移角和方案A-1(沿结构全高布置阻尼器)的最大层间位移角较为接近,角柱的最大顶部位移也相近,角柱最大层间位移角、中柱最大顶部位移和最大顶部加速度较方案A-1的指标还有差别,但差别不大,由此可见,如果布置阻尼器数量有限,选择底部布置方案B-1是较好的方案。
3.3.2 风振吸收能量
底部布置方案B-1、中部布置方案B-2和顶部布置方案B-3三种方案的风振吸收能量如表4所示,随着阻尼器布置数量的减少,阻尼器所吸收的能量也相应减少,方案B-1的其他构件吸收能量比方案B-2和方案B-3吸收的能量少,但是比A类方案四种布置形式所吸收的能量都要多,所以从其他构件所吸收的风振能量角度分析,阻尼器的布置数量起主导作用。

表4 三种阻尼器布置方案的风振吸收能量 J
4 结 论
本文针对特定的基本风压和地面粗糙度类别,运用AR模型获得总风压时程函数,以20层立体车库为研究对象,用风振时程分析方法研究了不同阻尼器布置方式对立体车库风振性能的影响,得到最优阻尼器布置方法,分析结果显示:
(1)通过自回归模型模拟的总风压时程函数可以很好地体现风荷载的动力特性,对于比较复杂的结构可以采用风振时程分析方法计算风荷载作用下的风振响应。
(2)为了得到粘滞阻尼器,可以通过使粘弹性阻尼器的刚度参数置为0,从而排除了阻尼器刚度对结构的影响,仅引入附加阻尼,这种方法可以推广应用。
(3)在原结构附设粘滞阻尼器后,A类方案和B类方案的几种阻尼器布置形式都有一定的减振效果。在阻尼器布置数量充足的情况下,A类方案考虑沿结构全高隔层布置粘滞阻尼器,在四种布置形式中,方案A-1的中柱和角柱的减振率分别为29.2%,36.1%,其他构件吸收的风振能量为715 J。方案A-1的最大风振吸收能量最少,由于阻尼器吸收的能量与阻尼器数量有关,这样方案A-1的其他构件吸收能量也最少。所以从减振率和吸收的风振能量来看,方案A-1效果最好。
(4)结构吸收的风振能量与阻尼器数量有直接关系,如果为了节省阻尼器数量,应该选择底部布置(第3,5,7,9,11层隔层布置)阻尼器的方案B-1,顶部布置方案B-2和中部布置方案B-3对于原结构的风振响应没有太大的改观,而底部布置方案B-1使结构风振响应明显减小,中柱和角柱减振率分别为27.7%,20.8%,可以兼顾经济和减振的要求。
