基于SA-LS-SVM的特殊地质条件下影响地铁盾构施工效率的地层参数分析

陈 伟， 胡耀越， 叶万敏， 常 嘉， 马 昊

(1. 武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070； 2. 武汉地铁集团有限公司， 湖北 武汉 430079)

地铁隧道工程施工过程中面临的地质条件越复杂，碰到含不良地层的特殊地质环境概率越大。由于不良地层地段的地层岩性、分布、厚度及性能变化较大，造成的刀具贯入度低、无法连续正常掘进等问题时常发生，甚至存在长时间停机的风险。盾构机在此地质条件下盾构时长明显增加，盾构施工效率显著降低，从而影响施工进度、增加施工成本。因此，在特殊地质条件下盾构掘进施工前对盾构施工效率进行预测研究，并对关键影响因素进行分析与预控，有利于工程进度计划的顺利进行与施工成本的有效控制。

盾构施工效率是学界的热点研究问题，有学者运用线性回归方法探讨掘进参数与掘进效率之间的关系，以尝试提高盾构施工效率[1]；而地铁盾构工程往往存在复杂、非线性的特征，又有学者进行改进，如利用神经网络建立预测模型对掘进参数进行优化，能及时有效地指导施工[2,3]；因神经网络等方法存在对大样本的依赖性、训练过拟合等缺点，作为新一代机器学习算法的支持向量机方法又被引入到建立掘进参数与推进速度之间的预测模型中，有效解决了地铁盾构工程存在的小样本、高维度的数据问题[4]。可以看出，学者们不断在进行探索优化，但现有研究成果多集中在掘进参数优化方面，如何结合特殊地质条件下地层参数角度开展研究还不多见。虽有学者尝试将地层参数作为输入变量，建立掘进参数的预测模型[5,6]，但仍未直接建立地层参数与盾构施工效率的关联性，模型精度有待提高。因此，有必要从特殊地质条件下地层参数角度对盾构施工效率进行针对性研究，并准确提取出对盾构施工效率较敏感的地层参数，为施工方案的合理选取提供依据，从而有效提高盾构施工效率，进而优化施工进度与施工成本。

鉴于此，本文以武汉市地铁隧道工程项目所涉及的含高伊利石和绿泥石的风化泥岩典型特殊地质为例，首先基于SPSS软件对盾构施工效率的影响因素进行分析，并选定关键的地层参数；再将模拟退火(Simulated Annealing，SA)算法与最小二乘支持向量机(Least Squares and Support Vector Machine，LS-SVM)相结合，利用SA搜寻LS-SVM的最优参数，并将地层参数作为输入变量，建立了盾构施工效率预测的SA-LS-SVM (Simulated Annealing and Least Squares and Support Vector Machine)模型，并通过预测模型对增加的施工成本进行评估；在SA-LS-SVM模型基础上，采用Sobol’法对关键地层参数进行灵敏度分析，准确辨识出影响盾构施工效率，进而影响施工成本的敏感参数，以期能更准确地确定有针对性的施工方案，在保证工程质量的前提下提高施工进度，优化施工成本。

1 盾构施工效率影响要素确定

为确定特殊地质条件下盾构施工效率的关键影响因素，对其直接影响因素即掘进参数进行分析，从而确定根本影响因素，再选取关键的根本影响因素作为盾构施工效率的影响要素，对盾构施工效率进行分析。

1.1 地质条件对掘进参数的影响

泥水平衡盾构机在掘进过程中，主要掘进参数有掘进速度、刀盘转速、刀盘扭矩、总推力及泥水仓压力[3,7]，它们不仅能反映盾构机掘进状态的变化，还能反映盾构机的掘进效能，是影响盾构施工效率的重要指标。因此，本文选取这5个主要掘进参数作为统计分析的基础数据，即根据地层的变化，分别在含高伊利石和绿泥石的泥岩特殊地质盾构区间以及正常地质盾构区间中各选取60环的掘进参数作为基础数据，研究不同地质条件对掘进参数的设置是否存在显著影响。基于SPSS软件，分别对5个掘进参数进行正态性检验以及方差齐性检验，结果均不满足要求，故本文选取非参数检验对数据进行分析，分析结果如表1所示。

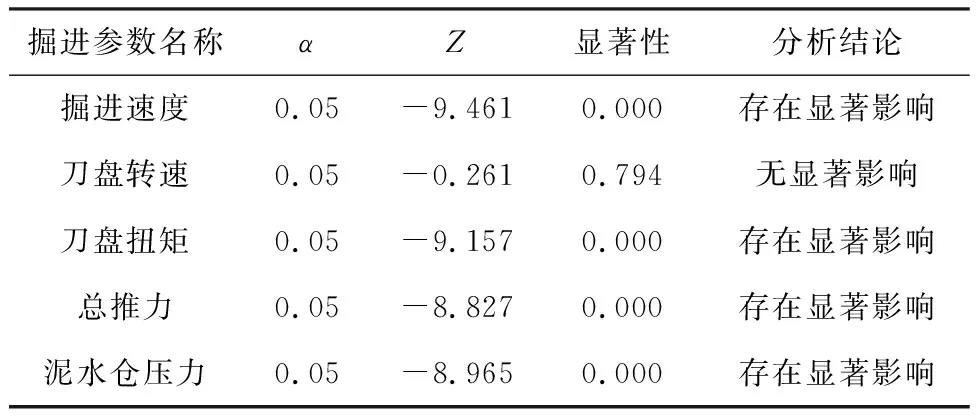
表1 非参数检验

从表1中可以看出，地质条件对掘进速度、刀盘扭矩、总推力、泥水仓压力的影响是显著的；而地质条件对刀盘转速的影响并不显著。事实上，非参数检验情况下地质条件对刀盘转速无显著影响，并不代表地质条件对刀盘转速没有影响，根据掘进参数施工记录资料显示，不同地质条件下的刀盘转速存在一定区别。这主要是因为在地铁盾构施工过程中，盾构工程师会根据地面监测结果反馈、通过建筑物等因素对参数进行实时调整，可以说人员操作是刀盘转速的主要影响因素。

通过以上分析可知，虽然掘进参数是影响盾构施工效率的直接因素，但地质条件才是影响盾构施工效率的根本因素，而地层参数是对地质条件的综合反映。因此，本文将地层参数作为盾构施工效率的主要根本影响因素。

1.2 关键地层参数的确定

土体粘聚力c、土体内摩擦角φ、泊松比v、弹性模量E为土体重要物理力学性质参数[8]，其中v与E是反映土体变形的参数，决定了土体的剪切模量，剪切模量越大，表明土体抗剪强度越大，越难以发生剪切破坏，故而难以切割，反之则相反。c与φ是反映土体强度的参数，是对土体进行作业过程中切削阻力的主要因素，是反映土体切削难易的一个重要方面。结合地勘资料，通过向施工单位访问得出渗透系数k是土体透水能力强弱的综合体现，在盾构施工时，k与盾构机往土层注水的难易程度有关，关系到盾构机的向前推进。这5个参数涉及到隧道工程建设的安全性、经济性和稳定性，故本文选取土体粘聚力c、土体内摩擦角φ、渗透系数k、泊松比v、弹性模量E为关键地层参数，作为研究盾构施工效率的影响要素，部分土体地层参数取值如表2所示。

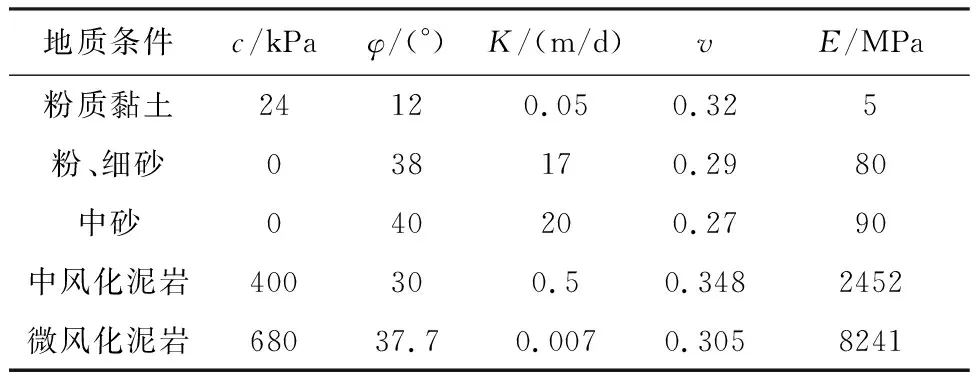
表2 土体地层参数

2 盾构施工效率分析模型

为对盾构施工效率进行有效分析，采用SA-LS-SVM对实际工程监测数据进行函数拟合，将地层参数作为输入变量，构建能反映地层参数与盾构施工效率关系的预测模型。为评价地层参数对盾构施工效率的敏感度，在参数分布空间内对地层参数进行两次独立抽样，并将抽样数据作为输入变量代入SA-LS-SVM预测模型进行计算，利用Sobol’法对计算结果进行全局灵敏度分析，获得地层参数的敏感性分布。

2.1 SA-LS-SVM盾构施工效率预测模型建立

为简便计算、提高速度，Suykens等[9]在支持向量机(SVM)的基础上提出了最小二乘支持向量机(LS-SVM)，LS-SVM克服了大样本的依赖性，能较好地解决小样本、高维度等数据问题，在各大领域被广泛应用[10]。由于地铁盾构施工环境复杂，其数据往往存在小样本、非线性、高维度的特点，故文中选用LS-SVM建立盾构施工效率的预测模型。

针对地铁盾构施工效率问题，本文选择非线性映射能力较强的高斯径向基核函数(Radial Basis Function，RBF)，由LS-SVM方法原理[11]可知，容错惩罚系数γ(其定义了拟合误差的容忍度，即决定了模型的泛化能力)和内核参数I(其定义了单个样本对整个分类超平面的影响，即决定了数据映射到新的特征空间后的分布)对地铁盾构施工效率预测的精度有较大影响，考虑到模拟退火(SA)算法是一种启发式随机搜索算法，是高效的全局优化技术[12]，因此本文选择SA算法对参数γ和δ进行优化，SA-LS-SVM预测流程如图1(图中SA-LS-SVM预测模型：Y=f(X)=f(x1,x2,…,xm)，Y为盾构施工效率，X为输入的地层参数)所示。

图1 SA-LS-SVM预测流程

2.2 盾构施工效率影响参数全局灵敏度分析

灵敏度分析可分为全局灵敏度分析和局部灵敏度分析，局部灵敏度分析忽视了多个因素间的交互作用，而全局灵敏度分析考虑了多个因素同时变化时，因素间的交互作用以及对系统输出的影响[13]。Sobol’法是一种定量评估方法，其基于方差研究单个输入变量或多个输入变量之间相互作用对系统输出的影响[14]，是一种经典的全局灵敏度分析方法，可用于非线性、非叠加性模型，能分析参数间的高阶交互效应[15]，计算结果可靠，故文中选用Sobol’理论建立全局灵敏度分析模型。其基本原理可描述为将函数f(x)分解为2m个递增项之和，通过计算模型参数的输入对输出方差的影响，从而求得各阶灵敏度系数[16]。

由于建立的盾构施工效率预测模型具有较大的复杂性和非线性，因此将灵敏度分析模型方差通过蒙特卡洛方法进行估算。假设地层参数在分布空间内分别进行两次独立抽样，样本为Sn×m，Hn×m，其中n为样本规模、m为地层参数个数，具体估算公式如式(1)～(6)所示：

(1)

(2)

(3)

(4)

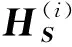
(5)

(6)

式中：Si为输入的地层参数xi单独作用时对盾构施工效率的影响，Si越大表明参数xi的不确定性对盾构施工效率的影响越大；STi为地层参数xi的各阶灵敏度系数的总和，表示该参数单独作用及其与其他参数交互作用对盾构施工效率的共同影响。故当参数xi的Si与STi相差较大时，可认为该参数与其余地层参数之间存在明显的交互作用。

3 实证分析

3.1 工程概况

武汉地铁A号线某泥岩区间工程采用泥水平衡盾构机施工，区间工程沿线地层条件较为复杂，泥水盾构不仅要穿越粉质黏土、粗砂等地层，还会遇到微风化泥岩、中等风化泥岩、强风化泥岩等不良地质环境。区间工程的泥岩X衍射试验报告表明，该区间泥岩矿物主要由绿泥石和伊利石等组成，其中，绿泥石含量高达15.78%，伊利石含量高达15.37%，这些高含量矿物都具有强大的离子交换能力和亲水性以及优异的吸水膨胀能力和吸附能力。

以往泥岩掘进中并未遇到本次高伊利石和绿泥石含量的泥岩，且以往所遇到的泥岩对盾构掘进影响较小，而此次含量较高、较为罕见，具有特殊性和不可预见性。在掘进过程中，高含量的伊利石和绿泥石使得刀盘切削形成的微粒易吸附于金属表面，形成刀盘泥饼、泥水仓中心泥饼，导致掘进参数不佳，掘进难度加大，部分工程数据如表3所示，可以看出当在特殊泥岩中盾构掘进时掘进参数发生了显著变化，盾构施工效率明显降低。

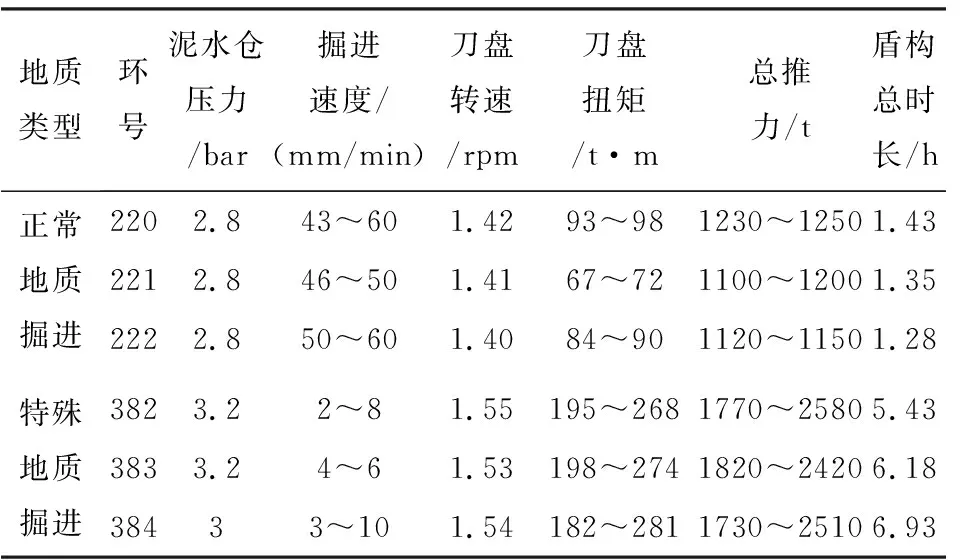
表3 部分工程数据

3.2 基于SA-LS-SVM模型的预测结果分析

3.2.1 盾构施工效率预测模型仿真结果分析

对数据进行拟合时，需将所收集的资料分为两类，一类是体现地质条件的输入变量即5个地层参数，另一类是体现盾构施工快慢的输出变量即盾构施工效率。地层参数的大小根据地勘资料确定，当同一开挖面含有不同地层时，根据开挖面各地层所占比重取各地层参数的加权平均值[7]。目前在盾构机方面，对盾构施工效率还没有较完整的定义，一般将掘进速度作为衡量盾构施工效率的唯一标准，但这两者并不等同，其中存在掘进时间与非掘进时间的差异。由于地铁盾构施工时以环作为计量单位，盾构机每掘进一环会停顿以进行盾构姿态测量以及管片安装等工作。因此为更贴近工程实际情况，本文以掘进每环所需时长为数据基础来研究盾构施工效率，盾构总时长越长，盾构施工效率越低，其中盾构总时长包括掘进时间、管片安装时间以及其他时间。

以武汉地铁A号线某泥岩区间工程监测的实际工程数据为基础，选取160组数据作为预测模型的拟合数据，其中随机选取90%的数据作为训练数据分别代入LS-SVM模型与SA-LS-SVM模型进行训练。

由于各参数量纲不同，故先对数据进行归一化处理，计算公式如式(7)所示，将处理好之后的数据代入模型进行训练。

F=(x-xmin)/(xmax-xmin)

(7)

式中：F为归一化后的数据；x为原始数据；xmax，xmin分别为数据组的最大值和最小值。

为检验改进后预测模型的有效性以及准确性，将其余10%的测试数据代入训练好的模型，LS-SVM预测模型与SA-LS-SVM预测模型的测试集拟合结果如图2所示，并计算相对绝对值误差，如表4所示。

图2 测试集拟合结果对比

测试集平均相对绝对值误差计算公式为：

(8)

式中：σ为测试集平均相对绝对值误差；fi为第i个测试样本预测值；ai为第i个测试样本实际值；nf为测试集样本数量。

由图2和表4可知，改进后模型的测试集平均误差为3.49%，最大误差为6.73%，相比于改进前，预测精度有明显提高，可以满足精度要求。

表4 模型优化前后对比 %

3.2.2 增加的机械台班费评估结果

工程资料显示，在特殊地质条件下盾构施工时，由盾构施工效率降低所引起的施工成本的增加可分为3类费用，包括工效调整类费用、消耗类费用与特殊地质改良费。其中消耗类费用和特殊地质改良费均与盾构施工效率存在直接的负相关线性关系，而工效调整类费用即增加的机械台班费，则需根据工效系数进行计算，故本文以机械台班费为例，验证建立的SA-LS-SVM预测模型对增加的施工成本评估的准确性，如式(9)所示：

(9)

式中：M1为增加的机械台班费；∑(Ti/li)/(N1t)为工效系数，Ti为泥岩掘进时第i个样本预测的盾构总时长，li为第i个样本的管片长度，N1为泥岩掘进总环数，t为正常掘进每延米的盾构时长；R为盾构机台班基本价；L为泥岩掘进长度。施工记录显示，在正常地质条件下平均掘进每延米需要1.05 h。

统计武汉地铁A号线整个泥岩区间共652环的地层参数，将地层参数带入训练好的SA-LS-SVM预测模型，根据预测结果，计算得出工效系数为3.33，依据《武汉城市轨道交通工程消耗量定额及基价表(试行)》，机械台班基本价为1978.79元/m，则增加的机械台班费用测算结果如表5所示。

表5 增加的机械台班费

由表5可以看出，通过对盾构施工效率的有效预测可以准确地对增加的机械台班费进行评估，并且其余两类费用均与盾构施工效率存在负相关的线性关系，即盾构施工效率越高，所需费用越低。因此，建立的SA-LS-SVM预测模型可对施工成本进行准确评估，进而为施工成本的预控管理提供参考，优化施工成本。

3.3 灵敏度分析结果

通过对武汉地铁A号线某泥岩区间工程进行研究，可知，由于地铁盾构的特殊地质环境，导致施工难度剧增，盾构施工效率严重下降，盾构耗材倍增，进而使盾构施工的相关费用随之大幅度增加。而目前对于结合特殊地质条件，如何提高盾构施工效率的经验知识相当有限，存在因知识不足而产生的认知性缺陷，对盾构施工效率的有效提升是非常不利的，另外，若在施工前对可能发生的风险应对措施准备不足，在盾构掘进过程中解决突发事件所花费的时间是很不经济的。

故本文结合特殊地质条件，在预测模型的基础上建立灵敏度分析模型，通过对地层参数进行全局灵敏度分析，可辨识出对盾构施工效率影响较大的地层参数，这些参数也会通过影响盾构施工效率，进而影响施工成本，施工时需对这些参数进行重点把控。

3.3.1 Sobol’法计算结果收敛性分析

为使得到的灵敏度系数结果稳健可靠，需要对其计算结果收敛性进行分析。由于拉丁超立方抽样(Latin Hypercube Sampling，LHS)能在较小的实验次数下得到较满意的实验结果，且LHS呈现了良好的分层效果[15]，故本文采用LHS对数据进行采样。设定基础样本量为6000，在6000个基础样本中分别按步长20抽取20，40，…，6000等子样本共计300组数据进行运算，得到的一阶灵敏度系数与总阶灵敏度系数的收敛结果如图3，4所示。可以看出，灵敏度系数在基础样本为4500之后上下波动幅度减小并趋于平稳。因此，选择基础样本数为6000时，所计算的灵敏度系数是稳健可靠的。

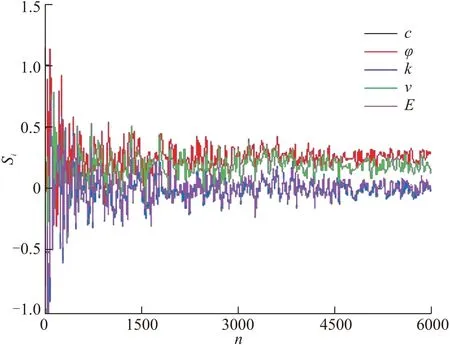
图3 一阶灵敏度系数

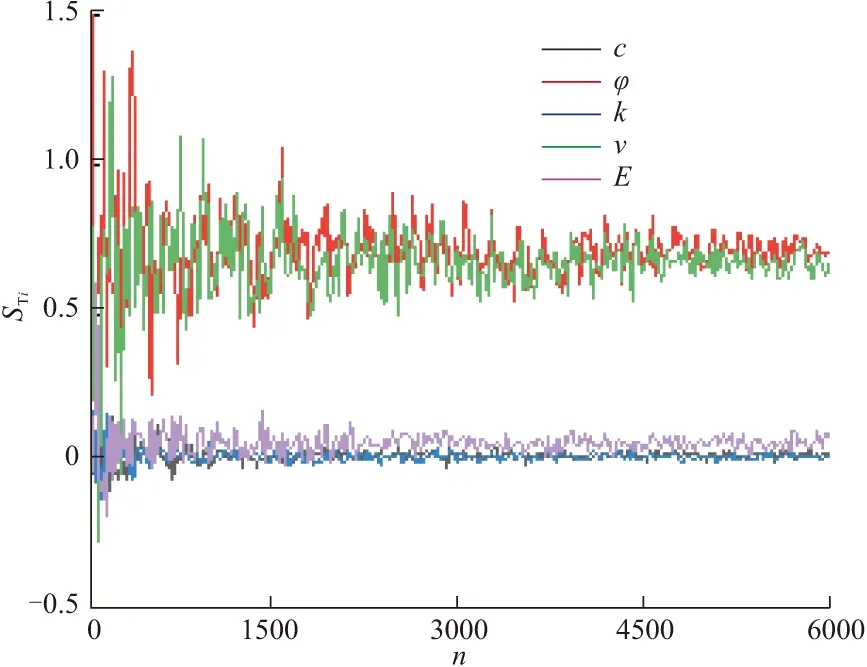
图4 总阶灵敏度系数

3.3.2 特殊地质条件下的参数灵敏度分析

地层参数的取值范围根据工程监测实际数据取值波动范围确定，采用拉丁超立方抽样在各参数取值范围内分2次选取6000个抽样值，构造2个6000×5的数据集，将数据集输入训练好的SA-LS-SVM预测模型，输出对应的盾构时长，在此基础上，利用Sobol’法对各地层参数进行全局灵敏度分析，进而得到各参数对盾构施工效率的影响程度，该影响程度也可作为评价地层参数对施工成本敏感度的重要依据，地层参数取值范围如表6所示。

表6 地层参数取值范围

为减小系统随机误差，将模型在基础样本数为6000时运行30次，取各地层参数的灵敏度系数平均值作为最终结果，各地层参数的一阶灵敏度系数Si与总阶灵敏度系数STi如图5所示。

图5 地层参数灵敏度

由图5可知，各地层参数对盾构施工效率的影响存在一定差异。只考虑参数单独作用，各地层参数对盾构施工效率的影响程度依次为：φ，v，E，k，c。考虑参数交互作用时，各地层参数对盾构施工效率的影响程度依次为：φ，v，E，c，k。

可以看出，无论是只考虑参数单独作用还是考虑参数的交互作用，φ均为最敏感的参数，这意味着当φ取值变化较大时，此盾构工程面临着较大的盾构施工效率波动的风险；v灵敏度系数稍低，但远大于其它三个地层参数，表明v也为较敏感因素；φ，v，E的Si与STi排序一致，这表明φ，v，E无论是只考虑参数的单独作用还是考虑参数间的交互作用，对盾构施工效率的影响强弱排序都是一致的，且φ，v，E与其余参数的交互作用均比其各自对盾构施工效率的影响更明显，表明在特殊地质条件下，φ，v，E均与其他参数间存在明显的交互作用，并更多的以与其他参数的交互作用影响着盾构施工效率；k的Si大于c，但STi却小于c，这是由于c与其他参数的交互作用比k与其他参数的交互作用对盾构施工效率的影响更为显著。

综上所述，φ为最敏感的参数，故需对φ取值变化较大的地方加以重视，尽可能多地进行地质勘探、力学实验等，以获取充足的数据对其空间分布特征进行精细化描述；相对于φ而言，v的敏感性稍低，但远大于排名第三的E，因此，亦需对其加以重视；地层参数间的交互作用会对盾构施工效率产生影响，在施工过程中涉及到关键地层参数时，应充分考虑各地层参数间的交互作用，但k的总阶灵敏度系数只略高于其一阶灵敏度系数，表明它更多的以单独作用影响着盾构施工效率，施工时可忽略它与其他参数的交互作用。此外，特殊地质条件下施工时，添加剂的选择尤为重要，可根据地层岩土的化学分析报告，结合灵敏度分析结果，采用针对性的添加剂，并根据实际情况进行配比，根据施工情况进行使用。

4 结 论

充分利用SA寻找最优解的能力与LS-SVM对高维度、非线性、小样本数据的学习能力，构建SA-LS-SVM模型对盾构施工效率进行预测；在此基础上，建立基于Sobol’法的全局灵敏度分析模型，探究复杂非线性样本数据情况下各地层参数交互效应对盾构施工效率的影响，以进一步辨识出敏感参数。论文的主要结论有：

(1)构建的SA-LS-SVM盾构施工效率预测模型，测试集平均相对绝对值误差为3.49%，符合精度要求；基于该模型对增加的机械台班费进行预测，误差为-2.92%，可推广运用于存在小样本、高维度、非线性数据问题的工程成本预控管理。

(2)各地层参数对盾构施工效率的全局灵敏度由高到低依次为：内摩擦角、泊松比、弹性模量、粘聚力、渗透系数。其中，渗透系数更多的以单独作用影响着盾构施工效率，施工时可忽略它与其它地层参数的交互作用；内摩擦角为最敏感的影响因素，应加以重视，对其变化特征进行详细描述。结果可为项目管理人员提供更加科学的决策依据与更加有效的施工进度管理。

本文从地层参数角度对盾构施工效率展开分析。地层参数间的相互作用对盾构施工效率存在显著影响，加强模型参数间的相关性分析可作为延伸的研究方向。