电磁场下神经元模型中混合簇的分岔机制1)

冀文超 段利霞 齐会如

(北方工业大学理学院,北京 100144)

引言

呼吸是一种重要的生理活动,是包括人类在内的所有哺乳动物维持生命的必要条件之一.研究发现,哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger 复合体(简称为pre-BötC) 中的条件起搏神经元的同步活动引起的[1-2].此后,生理实验研究证实了pre-BötC 是呼吸节律产生的主要部位[3],是离体实验中呼吸节律产生的关键[4].实验结果表明gNaP和gLeak代表亚阈电导的函数集,赋予pre-BötC节律性特征[5].光子成像测量树突状Ca2+瞬态的实验表明,呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6].此外,药物刺激也可对pre-BötC 的呼吸节律产生影响[7-12],这表明pre-BötC 可能与人类某些神经系统疾病有关,在呼吸节律的神经控制中占有重要地位.

神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究.王如彬等[13-14]研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用.古华光等[15-17]研究了神经系统中丰富的动力学行为[15-17].魏梦可等[18]和马新东等[19]对各种复杂簇发振荡行为及其产生机理进行了研究.Duan 等[20]研究了pre-BötC 在washout滤波器控制下的簇放电模式及转迁机理.程璇和刘深泉[21]对房室化神经元Chay 模型进行了非线性动力学分析和神经计算.持续钠电导(gNaP)和钙激活的非特异性阳离子电导(gCAN)对pre-BötC 的节律有重要影响,电导的变化会引起一系列放电节律的产生,如峰放电、方波簇、DB 簇以及由方波簇和DB 簇组成的混合簇(mixed bursting,MB)[22].混合簇是一种特殊的胞体-树突状簇,其特征是在每个周期内包含两种或更多种不同类型的簇.Desroches 等[23]介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制.Bacak 等[24]研究了pre-BötC 中的混合簇振荡模式.Wang 等[25]从多时间尺度和分岔分析的角度,研究了混合簇产生的动力学机理.Lü等[26]探讨了pre-BötC 吸气神经元单室模型中的MB 解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制,这些工作说明了混合簇在理论及实验研究中的重要性.

电磁场对神经元放电活动的影响也成为近年来的研究热点.Zhan 和Liu[27]研究了具有电磁辐射或高斯白噪声的Morris-Lecar 模型,发现电磁感应可以将簇或峰放电转换为静息态.Duan 等[28]研究发现,磁通量使pre-BötC 神经元在电流值较低的情况下振荡,改变外激励条件,可以观察到常规簇和混合簇类型.Guo 和Lü[29]研究了磁流和外部刺激电流这两个因素对单个pre-BötC 神经元混合簇放电模式的影响.Ma 等[30]利用磁通和电荷分别描述磁场和电磁感应、电场的变化,考虑电磁场的影响建立新的神经元模型,在这种新的神经元模型上进行了非线性分析,并应用外部电磁辐射来检测神经元活动中的模式转换.随后,他们又设计了一种简单的神经电路,通过结合两个物理电子元件来估计磁场对神经元活动的影响[31].虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32-35],但是其对混合簇的影响的研究还不够深入,还有很多值得进一步研究的内容.

本文通过对模型的分析和计算,研究外部刺激电流和磁通量对混合簇放电模式的影响,包括:(1)借助无量纲化分析,将模型中变量的时间尺度进行划分,无量纲化结果表明模型包含快、慢和超慢3 个时间尺度;(2)通过无量纲化后的模型研究外部刺激电流I和磁流反馈系数k1对混合簇放电模式的影响,并通过分岔分析来研究混合簇产生的动力学机制.结果发现,减小I和k1的值会使混合簇中胞体簇的个数减少,同时使簇的放电类型发生改变.全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间来回跃迁,导致混合簇的产生.研究结果可为深入了解电流和磁流对神经元的影响提供参考.

1 模型描述

Butera 等[36]建立了最小pre-BötC 神经元模型,该模型由钠电流(INa) 和钾电流(IK) 产生动作电位并通过持续钠电流(INaP) 的缓慢失活来终止放电过程.Toporikova 和Butera 把这一模型发展为具有胞体-树突双室的神经元模型(TB 模型)[37],该模型使用Butera 描述的pre-BötC 神经元模型作为胞体室,而树突室仅包含钙激活的非特异性阳离子电流(ICAN).Park 和Rubin[38]发现当TB 模型简化为单室时会定性地产生相似的动力学特征.

根据电磁感应的物理定律,带电离子在膜上的持续交换会引起离子浓度的复杂变化.神经元的膜电位波动被认为是电磁感应效应[39].因此需要建立随时间变化的电磁场来调节神经元的膜电位,而跨膜磁通量可以满足这一要求.磁通量φ 作为附加变量来描述电磁感应和电场的影响、检测电磁场的变化,且用来模拟磁通量的忆阻器能够与神经元膜电位的物理单位保持一致.Wu 等[30]通过设计一个带有外刺激电流和忆阻器的HR 模型的神经元电路图证明了带有外部刺激的电流和磁通量的模型的有效性[40].

本工作在Park 和Rubin[38]提出的pre-BötC 单室细胞模型中引入了电流和磁通控制忆阻器.模型描述如下

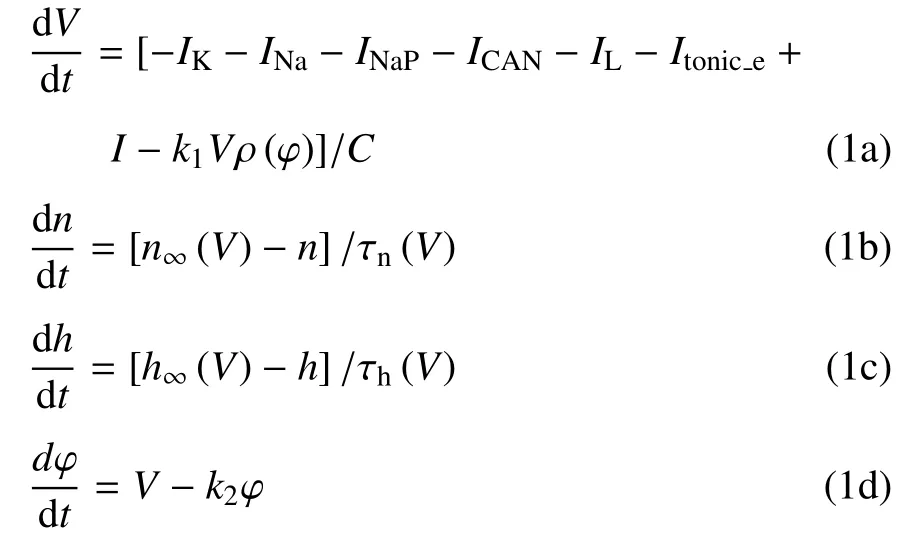
钙动力学为

式中,V是膜电位,C是膜电容,n和h是电压门控钾和钠通道的门控变量.IK,INa,INaP,ICAN,IL和Itonice分别代表钾电流、钠电流、持续钠电流、钙激活的非特异性阳离子电流、漏电流和兴奋性刺激产生的电流.I是外部刺激的直流电.[Ca]是指细胞内钙浓度,l表示未被灭活的IP3通道,该通道会影响由JERIN和JEROUT表示的胞浆和内质网之间钙的通量.

磁通量φ 可以描述电磁感应和磁场的影响,而ρ(φ) 是磁通控制忆阻器的记忆电导,用来描述磁通量φ 与膜电位V之间的关系,其表达式为ρ(φ)=α+3βφ2,式中α,β 是给定的参数值.k1Vρ(φ) 用于描述电磁感应引起的感应电流.k1和k2描述膜电位与磁通量之间的相互作用.定义Iapp=I-k1Vρ(φ).各离子电流表示为

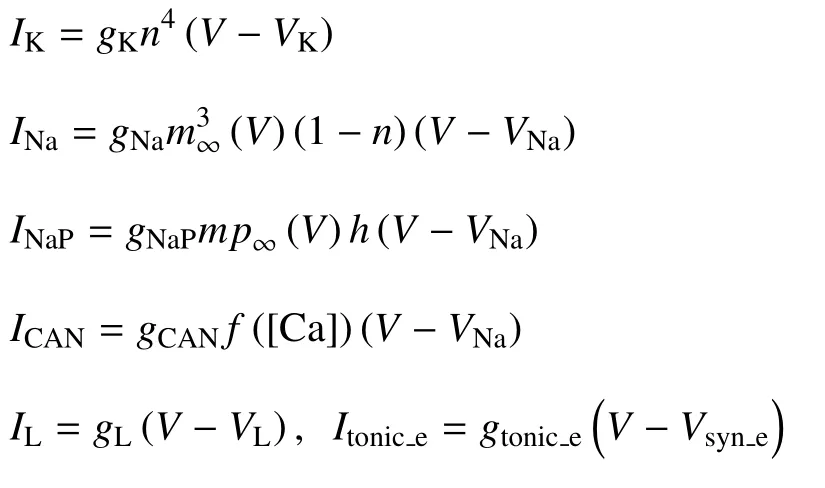
平衡函数n∞(V),h∞(V),m∞(V),mp∞(V) 具有如下形式

时间尺度函数

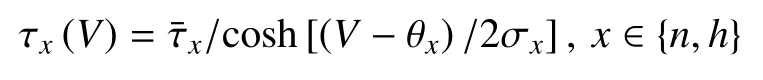
其他函数表达式

本文设置[IP3]=0.95 μmol/L,使[Ca]处于活跃状态,即呈现周期波动.参数取值详见表1.

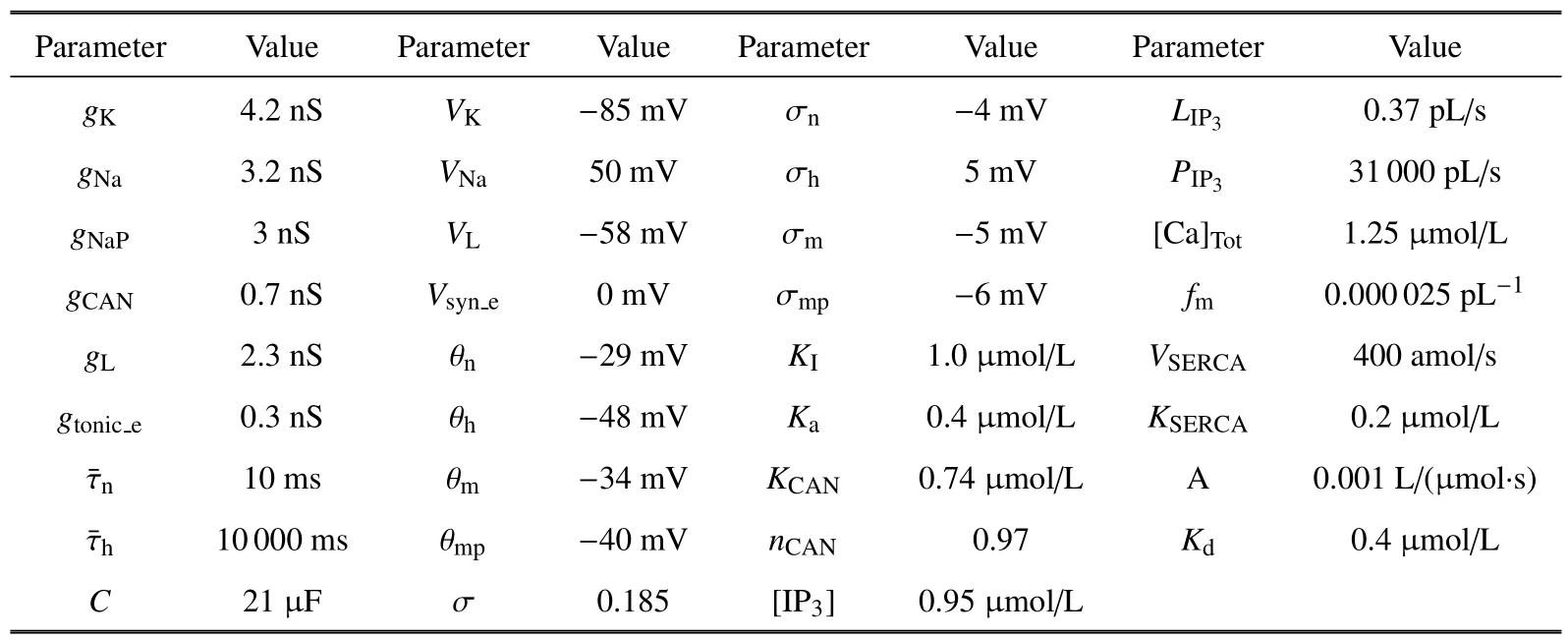
表1 模型中的的参数值Table 1 Parameter values in the theoretical model

2 主要结果

采用快慢分解的方法来研究系统放电模式的动力学.为了清楚地识别不同变量的时间尺度,对整个系统(1a)～(1f)进行了无量纲化处理[25].

2.1 无量纲化分析

重新对变量进行缩放来揭示各变量的时间尺度.为此,定义电压、钙、磁通量和时间的无量纲变量v,c,τ 以及其对应的标度,分别为Qv,Qc,和Qτ

注意到n,h和l在方程中已经是无量纲的.

由于膜电位V∈[-70,-5],在这个范围下定义Tx=max(1/τx(V)),x∈{n,h}和tx(V)=Txτx(V).而[Ca]∈[0,1],在这个范围下定义

把这些变量代入方程(1a)～(1f),得到以下系统

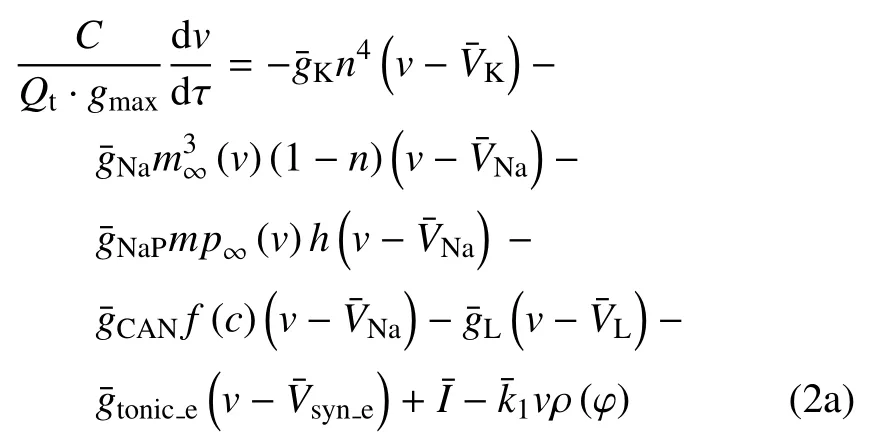
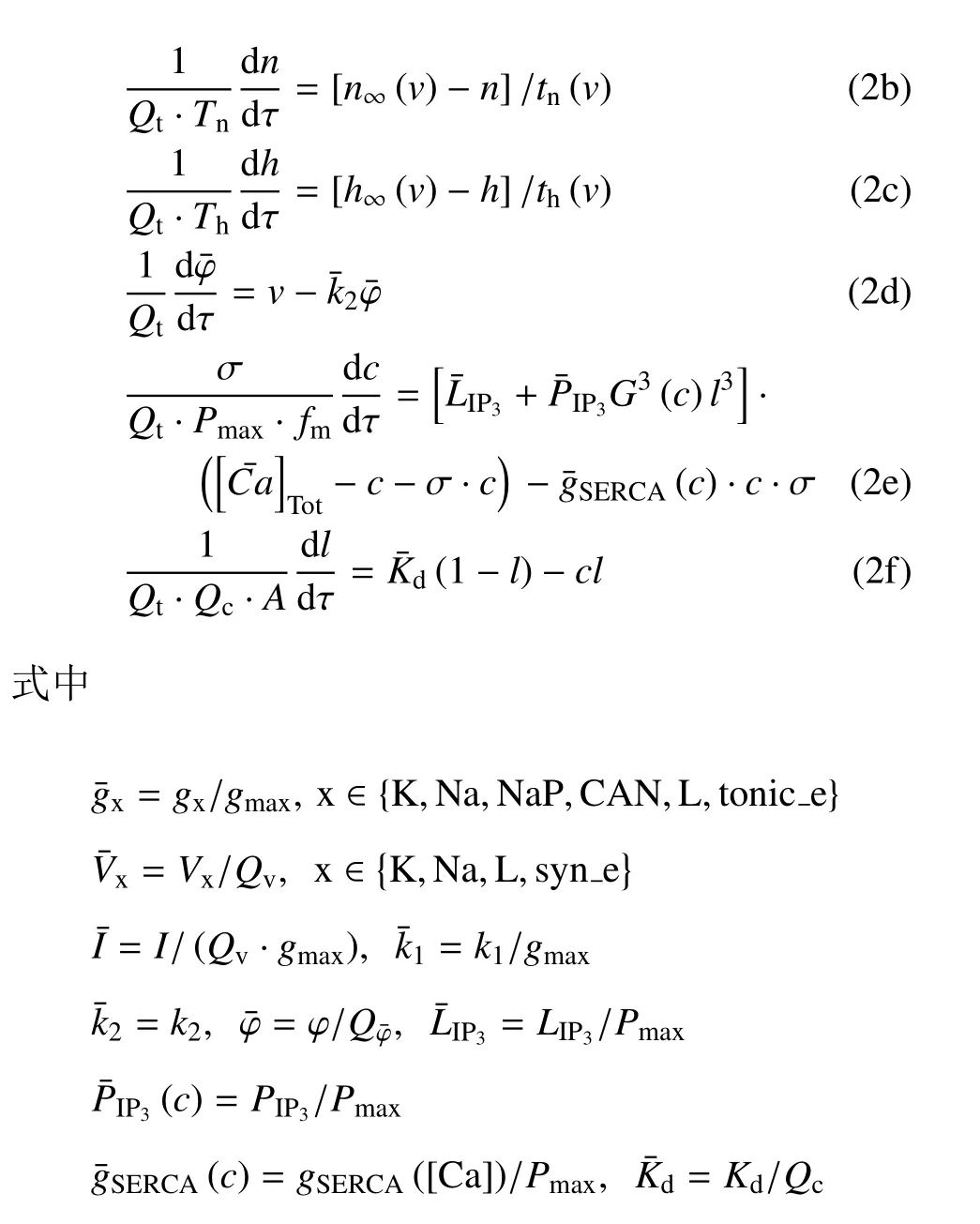
结合V,φ 和[Ca] 的范围,取Qv==100 mV,Qc=1 μm.m∞(V),mp∞(V),n∞(V),h∞(V),f([Ca])·G([Ca]),([Ca]),n,h和l的值均在[0,1] 范围内.结合表 1 中的参数值和文中变量的取值,gmax=|Imax|=35 μA.由1/τn(V) 和1/τh(V) 与V的关系可得:Tn≈2.5 ms-1和Th≈0.003 5 ms-1(如图1(a) 和图1(b)).同理,由Gc和GS与[Ca] 的关系可得Gc≈0.042 和GS≈1000 pL/ms (如图1(c)和图1(d)),故有Pmax≈1302 pL/ms.将这些值代入(2a)～(2f),可使方程(2a)～(2f) 右侧的所有项均以1为(绝对值)界.选择快时间尺度即Qt=1 ms 作为参考时间,方程左边导数的系数能够揭示变量的相对变化速率

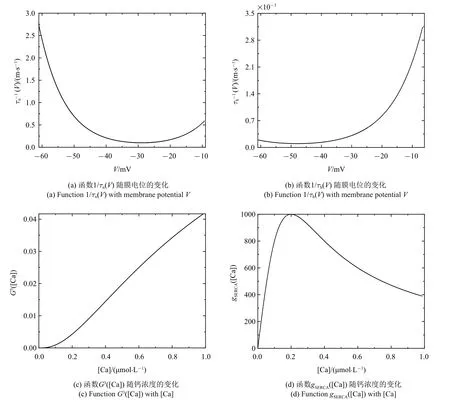
图1 无量纲化过程中的函数图像Fig.1 Function graph in the nondimensionalization process

令

则无量纲系统(2a)～(2f)即为系统(4a)～(4f)

式中Rv,Rn,Rh,,Rc和Rl是方程(3a)～(3f)中给出的无量纲参数.

所有变量的整体相对比率为

由此可得v,n,在一个快速的时间尺度上演化,h和c在一个较慢的时间尺度上演化,而l在一个超慢的时间尺度上演化,即模型具有3 个不同的时间尺度.因此,上述模型可以被视作包含快、慢和超慢变量的动力学模型.方程(1a),(1b) 和(1d) 构成快子系统,(1c)和(1e)为慢子系统,方程(1f)是超慢子系统.无量纲变换后的参数取值详见表2.

表2 系统(4a)～(4f)中的参数值Table 2 Parameter values for system(4a)～(4f)

表2 中带顶标-的变量与表1 的变量有如下关系

改革开放40年中国社会经济的发展，是中国设计走向体系化、市场化，释放自身能量的过程。然而，回忆过往，中国能够建立全面、完整的工程设计体系，那些工程设计院（所）功不可没。

实验表明Ca2+振荡起源于pre-BötC 神经元的树突[41],因此仅在树突室中包含Ca2+动力学,其中Ca2+的动力学受细胞内Ca2+浓度[Ca]和IP3通道门控变量l控制.方程(1a)～(1f)称为全系统.当使用单室模型时,模型中没有树突部分,不过本文沿用Park和Rubin[38]的命名方式,称子系统(1a)～(1d) 为胞体子系统,子系统(1e)～(1f)为树突子系统.l的变化间接影响胞体子系统(1a)～(1d),因为l会影响[Ca],[Ca]会影响V,且这种影响是单向的,但l不直接出现在膜电位V的方程中,即树突子系统独立于胞体子系统,而胞体子系统却受到树突子系统的影响.下面主要对无量纲化之后的系统(4a)～(4f)进行研究.

2.2 无外界刺激(=0)时的放电模式和分岔分析

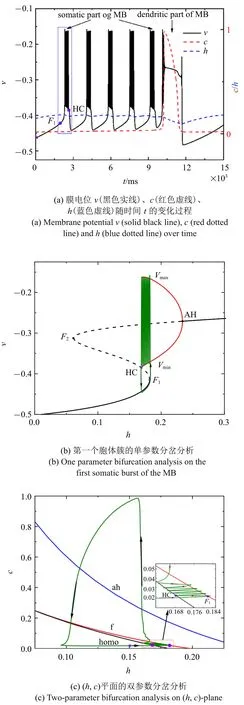
图2 =0 时的混合簇放电模式和分岔分析Fig.2 Firing patterns and bifurcation analysis when =0

无量纲化的结果表明,c和h都属于慢变量.但是在胞体部分c几乎不变,从而在胞体部分h的相对演化速率比c快.所以,在分析胞体簇时,可将慢变量h作为胞体子系统的分岔参数,而将c看作常数,研究快子系统的动力学.树突部分c的突然增大,导致在c和h两个慢变量中,c的相对演化速率比h快,故分析树突簇时要将慢变量c作为树突子系统的分岔参数而把h看做常数,即细胞内钙浓度是否产生波动不仅可以区分胞体部分和树突部分,而且可以决定每一部分的分岔参数.

由于混合簇中胞体部分的簇的类型都相同,所以只对第一个胞体簇进行分岔分析.以h为慢变量,取第一个胞体簇所对应的c的平均值为0.020 7,对应快子系统的分岔如图2(b)所示.平衡点形成S 形曲线,曲线的下分支(黑色实线) 和中支(黑色虚线) 分别由稳定结点和不稳定鞍点组成.曲线的上分支由稳定和不稳定的焦点组成,不稳定焦点经由Andronov-Hopf(AH)分岔变为稳定焦点,并在AH 分岔处产生稳定的极限环(红色实线).稳定极限环通过同宿轨分岔(HC)消失.点F1和F2表示平衡点的鞍结分岔.全系统的轨线(绿色曲线)也叠加在分岔图上.当慢变量h增大时,S 形曲线下支的静息态经由平衡点的鞍结分岔F1跃迁至上支的稳定极限环,并由于稳定极限环的吸引反复振荡,振荡态经由同宿轨分岔(HC)跃迁至下支的静息态,从而完成了一个周期振荡.根据Izhikevich 簇放电分类的标准[42],此时的簇放电模式为“fold/homoclinic”型簇放电.

快子系统在(h,c)平面上的双参数分岔如图2(c)所示,其中f,ah,homo 分别代表鞍结分岔曲线(红色),AH 分岔曲线(蓝色)和同宿轨分岔曲线(黑色).在本文选取的参数范围内,双参数平面中没有出现余维2分岔.全系统的轨线(绿色) 也叠加在(h,c) 平面上.插图是局部放大,分岔发生的关键点与图2(a)对应,(⋆)仍表示初始时刻.结果表明,(h,c)平面的全系统轨线为逆时针方向,随着慢变量c的逐渐增大,轨线在鞍结分岔曲线f和同宿轨分岔曲线homo 之间来回穿梭,意味着混合簇中胞体簇的产生与这两类分岔相关.全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁5 次,对应于混合簇中的5 个胞体簇.之后,c的突然增大,使得混合簇的胞体部分结束,转换到树突部分.

2.3 电流对混合簇放电模式的影响和动力学分析

表3 电流所对应的I 值Table 3 Values of current corresponding to I

表3 电流所对应的I 值Table 3 Values of current corresponding to I

图3 =-0.000 57 时的混合簇放电模式和分岔分析Fig.3 Firing patterns and bifurcation analysis when=-0.000 57

随着电流的减小,混合簇中胞体簇的个数也在减少.图4(a)～图4(c)分别是电流值=-0.001 43 时的全系统簇放电模式以及单、双参数分岔分析(c取平均值0.020 5).胞体簇的个数减少为4 个,与之对应,(h,c)平面双参数分岔分析中全系统轨线在鞍结分岔曲线与同宿轨分岔曲线之间跃迁4 次.此时,胞体簇的放电类型仍为“fold/homoclinic”型簇放电.

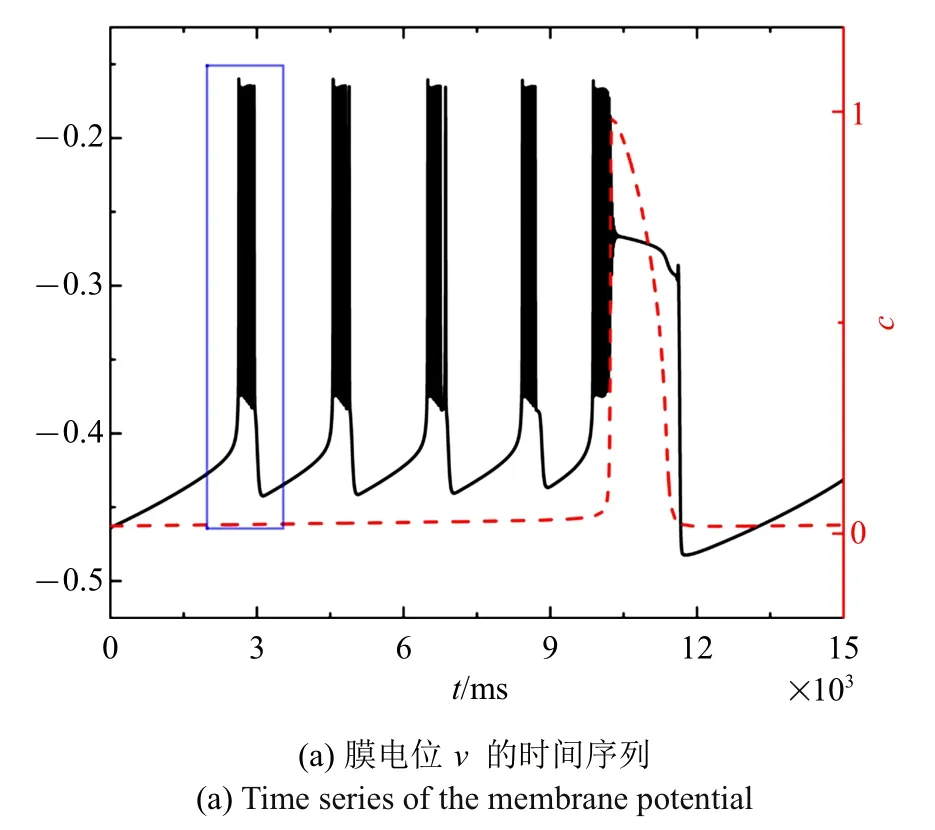
图4 =-0.001 43 时的混合簇放电模式和分岔分析Fig.4 Firing patterns and bifurcation analysis when=-0.001 43

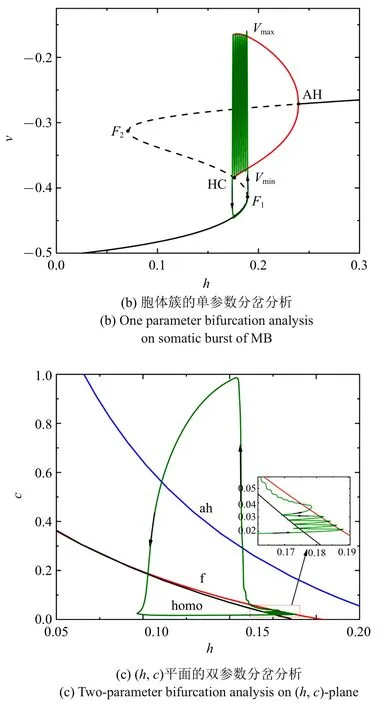
图4 =-0.001 43 时的混合簇放电模式和分岔分析(续)Fig.4 Firing patterns and bifurcation analysis when =-0.001 43(continued)

图5 =-0.004 29 时的混合簇放电模式和分岔分析Fig.5 Firing patterns and bifurcation analysis when=-0.004 29

图6 =-0.007 14 时的混合簇放电模式和分岔分析Fig.6 Firing patterns and bifurcation analysis when=-0.007 14

图7 =-0.01 时的混合簇放电模式和分岔分析Fig.7 Firing patterns and bifurcation analysis when =-0.01

图7 =-0.01 时的混合簇放电模式和分岔分析(续)Fig.7 Firing patterns and bifurcation analysis when=-0.01(continued)

本节给出了簇放电行为如何随¯I的变化而变化.利用快慢分解和分岔分析对不同电流值下的混合簇中的胞体簇进行分类,并揭示了混合簇的产生机制.随着电流值的减小,混合簇中胞体簇的个数逐渐减少,同时簇的放电类型发生改变.树突簇在不同电流值下的放电模式也有所不同.双参数分岔分析中,随着c的逐渐增大,全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁,意味着混合簇中胞体簇的产生与这两类分岔相关.全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁的次数,与混合簇中胞体簇的个数相对应.

2.4 磁流对混合簇的影响

表4 参数 所对应k1 的值Table 4 Values of parameter corresponding to k1

表4 参数 所对应k1 的值Table 4 Values of parameter corresponding to k1

图8 不同 值时的混合簇放电模式(=0)Fig.8 Firing patterns of mixed bursting with different=0)

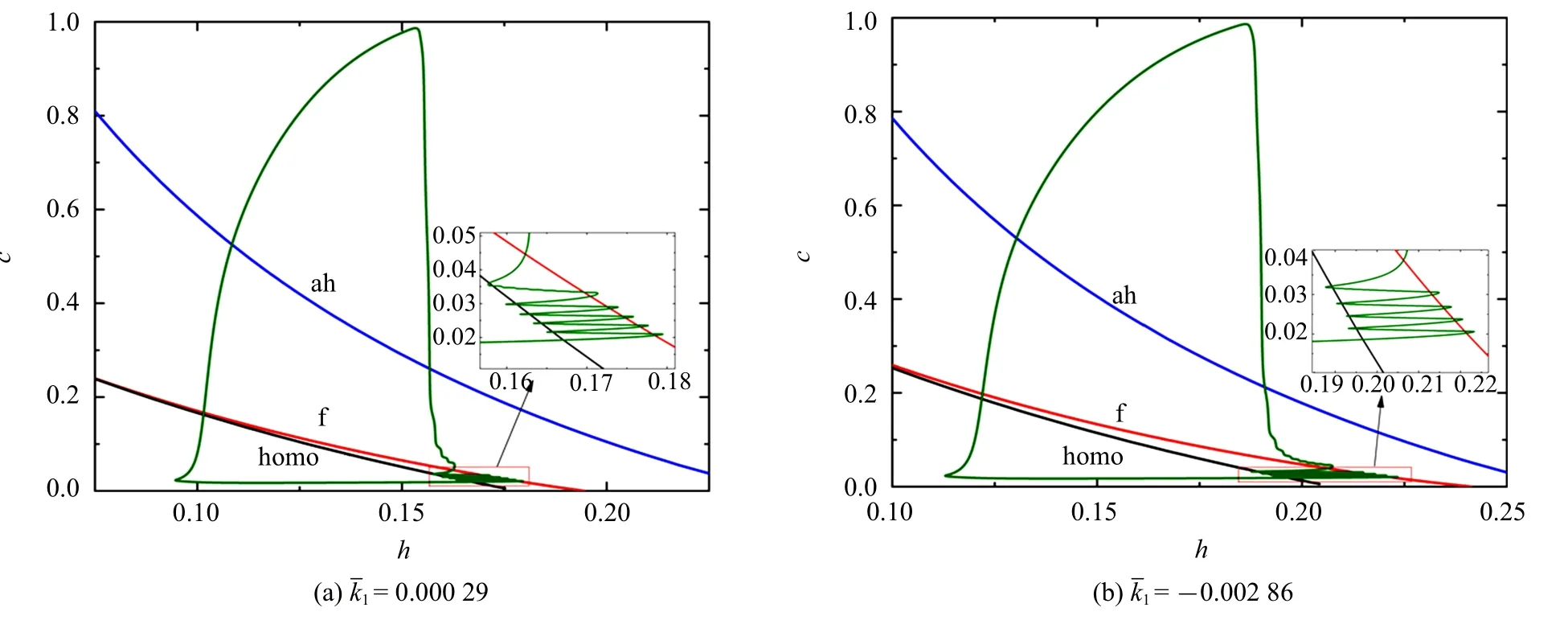
图9 不同 值时的双参数分岔分析(=0)Fig.9 Two-parameter bifurcation analysis with differentvalues(=0)

图9 不同 值时的双参数分岔分析(=0)(续)Fig.9 Two-parameter bifurcation analysis with different values(=0)(continued)

3 结论和展望

神经系统十分复杂,包括不同的空间层次、不同的功能状态(生理、病理和药理状态)和不同的动力学行为.参数激励下的多时间尺度非线性系统可以产生非常复杂的簇放电行为.探讨簇放电模式各种可能的诱发机制一直是簇放电研究的重要问题之一.虽然pre-BötC 神经元中混合簇放电行为已有一定的研究,但电流和磁流影响混合簇放电的研究不多.模型所描述的规律应该独立于量纲的影响,与已有的直接分析神经元动力学行为方法不同,本文排除量纲的影响,对模型进行无量纲化处理,利用无量纲量来分析神经元混合簇放电、转迁行为,保持了与原始数据变化趋势整体的一致性和关联系数一致性,为揭示神经元复杂动力学行为提供了新的分析方法,进一步丰富了神经元非线性动力学行为的内容.

本研究用忆阻器模拟磁通量,在Butera 神经元模型中引入电流和磁通量,应用多时间尺度及分岔分析的方法,分析电流和磁流对神经元混合簇放电模式的影响.通过无量纲化的方法对时间尺度进行划分,并用尺度变换后的无量纲动力系统进行分析.通过将混合簇分为胞体部分和树突部分[38],区分了混合簇放电模式并对胞体簇进行了动力学分析.研究表明:电流和磁流都可以显著影响pre-BötC 细胞的混合簇放电节律.减小电流和磁流反馈系数的值会使混合簇中胞体簇的个数减少,同时使簇放电类型由“fold/homoclinic”型簇放电转迁为经由“fold/homoclinic”滞后环的“Hopf/Hopf”型簇放电.利用双参数分岔分析,我们揭示了混合簇模式的产生机制.如果全系统轨线可以在鞍结分岔曲线和同宿轨分岔曲线之间跃迁,整个系统出现混合簇.上述研究结果可以加深我们对神经元放电动力学的理解,为电流和磁流对神经元放电模式的影响提供参考.

类似实验中,药物刺激可以使一个周期内只有一种类型的簇转化为周期内含有两种或多种类型的混合簇[43],发现外部电流刺激也可以达到同样的效果.设置k1=0.1,k2=3 s-1,α=1 mol/(L·Ω),β=0.000 06 mol/(L·Ω·V2·s2) 增大电流可使同一周期内含有两种或多种类型的簇,如图10(b) 所示.图10(a)是相同离子浓度时Iapp=0 的情况.对这一现象的动力学分析,更多讨论将在未来进一步研究.除此之外,也可以在模型中考虑噪声、时滞等因素,模拟更复杂环境下的神经元模型,对不同环境状态下的神经元模型进行动力学行为研究.

图10 不同电流值所对应的混合簇放电模式(gNaP=1.7 nS,gNa=4.2 nS,gK=1.4 nS,[IP3]=0.97 μmol/L)Fig.10 The mixed bursting corresponding to different current values(gNaP=1.7 nS,gNa=4.2 nS,gK=1.4 nS,[IP3]=0.97 μmol/L)