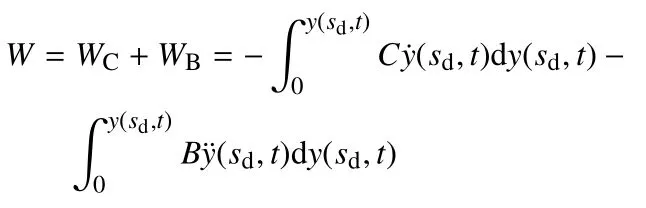接地惯容式减振器对悬臂输流管稳定性和动态响应的影响研究1)
2021-11-09郭梓龙贾青青杨文正
郭梓龙 王 琳 倪 樵 贾青青 杨文正
(华中科技大学工程力学系,武汉 430074)
引言
在当今迅速发展的工业时代,输流管道已成为众多工程装备的重要组成元部件.海洋工程中的海洋立管、核电装备中的管束结构等都是输流管道应用的典型实例.在管内流体的激励下,管道因流体-固体耦合作用可产生自激振动和有害噪声.当其他外界激励频率与输流管道固有频率相近时还可能引起共振,从而诱发受迫振动与自激振动的协同作用.事实上,输流管的流固耦合过程也表现出一种较强的非线性流固耦合特征,正因为如此,输流管结构的动力学问题研究已成为流固耦合力学领域的重要研究内容之一[1-7].
悬臂输流管道是典型的非保守系统,在流速较大时会丧失稳定性并发生动态的非线性颤振现象,这显著不同于两端支承输流管道只可能出现的静态屈曲失稳现象.悬臂输流管道失稳后的大幅颤振行为可加速管道构件的疲劳破坏,严重时甚至可造成不可估量的安全事故.
在学术界,输流管道出现失稳时的流速值被称为临界流速.近年来,人们通过对临界流速的调节已成为输流管动力学控制研究的一个重要内容;此外,还有学者采用各种控制方法来降低管道振动幅值,从而达到降低管道破裂或疲劳损伤等风险[8-15].
输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制,从理论上来看具有较好的控制效果[16-18].例如,Abbasnejad 等[19]研究了含有轴向分布压电层的微流体管道的稳定性,同时还探讨了支撑边界对稳定性的影响,其研究结果表明:通过对压电层施加电压差,可显著抑制流体对管道振动频率的影响,从而扩大了稳定性区域.Ge 等[20]通过对管道施加一个与时间相关的位移函数,采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制,验证了该控制方法的有效性.Szmidt 等[21]利用在悬臂管道上安装电磁装置的方式,使得运动中的电板在切割磁感线过程中产生阻力,以此来提高悬臂输流管的动态稳定性,也得到了较好的控制效果.
相比于主动控制,被动控制方式因其结构简单、不需要外界能量输入,且具有一定的鲁棒性等特点,在工程实践中得到广泛应用.输流管被动控制的方法有很多,比如动力减振器法[22-23]、阻尼器法[24-25]、非线性能量汇法[26-27]等.Zhou 等[28]通过在悬臂管道上安装非线性能量汇对管道振动进行控制,分析了不同能量汇参数对提高悬臂管道临界流速的影响.Gourdon 等[29]通过实验方法验证了不同类型激励下非线性能量汇的减振效果,其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果.Li 等[30]提出了一种冲击式调谐质量阻尼器(PTMD),通过质量块与黏弹性材料的碰撞方式来耗散振动能量,发现这种新型阻尼器可有效的控制振动.
近年来,有学者提出了将惯容器应用到结构的振动控制问题之中,获得了较好的被动控制效果[31-36].惯容器相比于传统的质量块而言体积更小.对于相同质量的惯容器和普通质量块,惯容器能提供更大的惯性效应,它产生的惯性力与其两自由端的加速度之差成正比关系,这使得惯容器方式已在多个工程实践中得到了应用.Shi 等[37]研究了在拉索一端安装接地惯性阻尼器,探讨了惯性系数和阻尼系数对拉索振动响应的影响规律,并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38]借助含有惯容器和负刚度的动力减振器对结构进行振动控制,发现相比于传统的动力减振器,这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看,现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中,但这类减振器对非保守的悬臂输流管系统是否有控制效果,目前还未可知.
本文针对悬臂输流管系统,试图通过安装带有接地惯容器的减振器,探究惯容器对悬臂管临界流速和动力学响应的影响.该惯容器既可产生惯性力,还引入了线性刚度、非线性刚度和阻尼等因素.首先,通过Hamilton 原理,给出了带有接地惯容器非保守输流管系统的控制方程;然后,借助数值方法进行求解,验证此控制方法的有效性;最后,通过典型算例分析,得到不同参数取值下惯容器对悬臂输流管道的控制效果.
1 理论模型
本文设计的减振器结构由线性弹簧、阻尼器、惯容器和非线性弹簧并联组成,安装在悬臂管道x=xb处,减振器的另一端连接在地面,如图1 所示.记悬臂管道沿y轴的横向位移用y(s,t)表示,它是管轴线曲线坐标s和时间t的函数.为方便研究,忽略管道的转动惯量和剪切变形;假设管内流速恒定不变;管道中心线不可伸长;管道可发生较大横向变形,但应变较小.
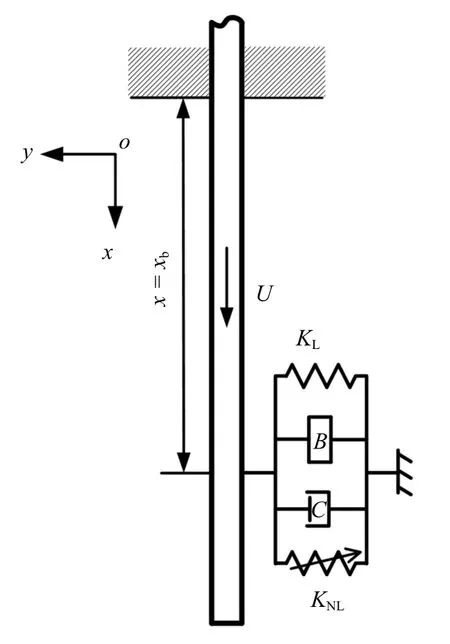
图1 带有惯容减振装置的悬臂输流管示意图Fig.1 Schematic diagram of a cantilever pipe with an inerter-based absorber
基于以上假设,引入广义的Hamilton 原理[4]
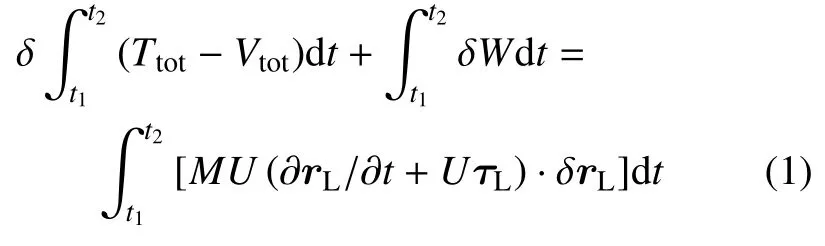
其中Ttot和Vtot分别表示悬臂管道系统的总动能与总势能,δW表示非保守力所做的虚功;式(1) 中等式右边项代表流体从管道自由端流出时所做的虚功,rL和τL分别表示管道末端的位置矢量和切线矢量.式(1)中系统的动能、势能与非有势力做功项的详细表达式可见附录,由该式可推导得出带有惯容减振器的悬臂管运动微分方程为
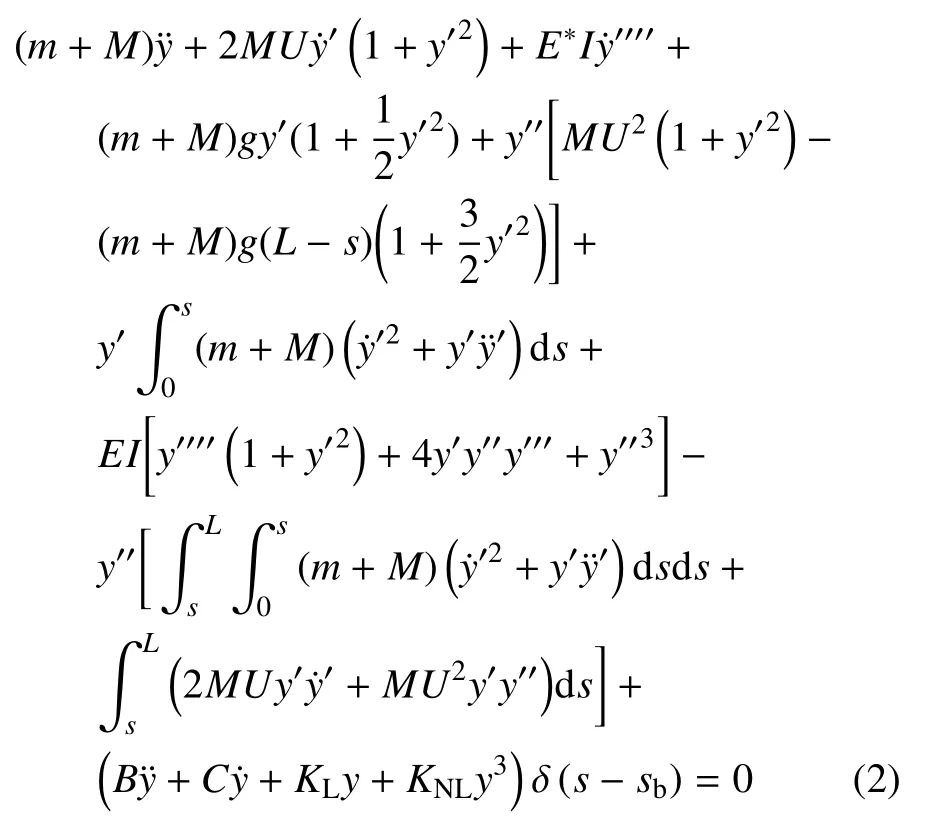
其中,L为悬臂管道长度,m为单位长度的管道质量,M为单位长度的流体质量,U为管道内流体的速度,EI为管道的抗弯刚度,E*为Kelvin-Voigt 阻尼系数,g为重力加速度,KL和KNL分别为线性和非线性弹簧刚度系数,B和C分别为惯容系数和阻尼系数,(′)和(·)分别表示对曲线坐标s和时间t的一阶偏导,δ(s)为Dirac delta 函数.
为方便分析,得到更有普遍性的结论,引入下列无量纲参数
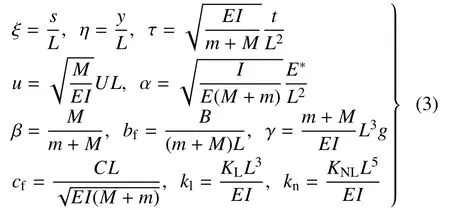
将式(3)代入运动微分方程(2)中得到无量纲化后的控制方程为

2 Galerkin 法离散化
借助Galerkin 方法对方程(4)进行离散化,取悬臂梁的前N阶模态函数进行截断近似,此时管道横向位移可写为

其中,φr(ξ) 是悬臂梁无量纲化的模态函数,qr(τ) 是相应离散系统的广义坐标,φ=[φ1,φ2,···,φN] 和q=[q1,q2,···,qN]T分别为特征函数和广义坐标向量.将式(5)代入无量纲方程(4)中,利用模态函数的正交性,在整个等式同时左乘φT并在区间[0,1]上积分后可得
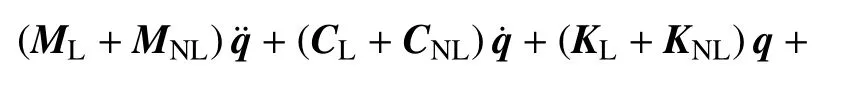

其中,ML和MNL为质量矩阵,CL和CNL为阻尼矩阵,KL和KNL为刚度矩阵,下标L 和NL 分别表示线性和非线性项;质量、阻尼和刚度矩阵的维数均为N×N;,)T和分别为管道离散系统所对应的广义坐标速度和广义坐标加速度,均为N×1 的向量.
悬臂管道无量纲化后的边界条件和初始条件选取为
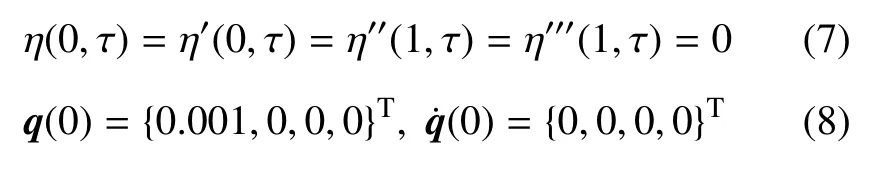
借助四阶龙格库塔方法对非线性常微分方程组(6)进行数值求解,可以得到输流管系统的非线性动力学响应.
3 算法验证
为验证本文算法的有效性,本节首先给出了无减振器作用的悬臂管道前四阶无量纲复频率随流速变化的Argand 图,如图2 所示.为确定该悬臂管道系统的临界流速,可将方程(6)线性化后得到如下形式的线性齐次方程组

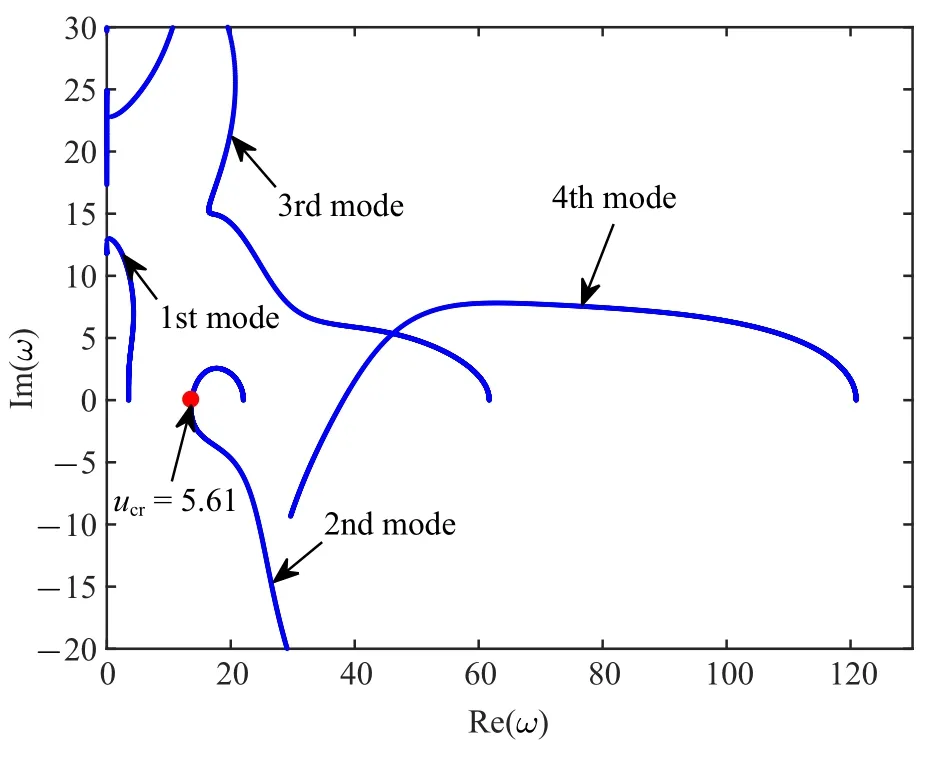
图2 无减振装置的悬臂输流管的Argand 图Fig.2 Argand diagram of the cantilevered pipe without vibration absorber
其中
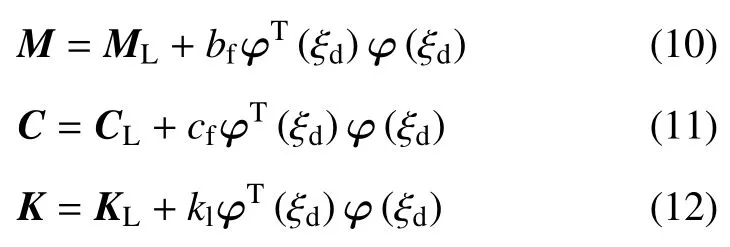
为了与Paidoussis[1]的经典结果进行对比,取参数α=0,β=0.2 和γ=0.记方程(6)的特征值λ=iω,则实部Re(ω)表示无量纲化的振动频率,Im(ω)表征了系统的阻尼.从图2 可知,随着管内流体速度的不断增大,第二阶模态阻尼从正值变为负值,这表明系统可以从流体中吸收能量,同时将能量传送给管道,此时系统会发生颤振失稳,管道因此而出现周期振动现象.从图2 还可看出,悬臂管第二阶模态发生颤振失稳的临界流速约为ucr=5.61.随着流速的不断增大,悬臂管的特征值演化曲线与文献[1]的经典结果是一致的,从而验证了本文方法所获得解答是可靠的.
若将惯容减振器安装在悬臂管道ξb=0.9 位置,且减振器各参数分别取值为bf=0.2,cf=0.5,kl=60和kn=8 000,管道的3 个关键参数仍取为α=0,β=0.2 和γ=0,可得到如图3 所示的Argand 图.从该图可以看到,引入减振器后的悬臂管道的临界流速从5.61 增大到6.94,且仍然是第二阶模态率先发生失稳,这显示本文所提出的减振装置能提高管道系统的稳定性.接下来,本文将进一步探讨减振器各参数对系统稳定性及非线性动力学行为的影响.

图3 含减振装置的悬臂输流管的Argand 图Fig.3 Argand diagram of the cantilevered pipe with vibration absorber
4 稳定性分析
本节主要对带有减振器的悬臂管稳定性进行分析,考查不同减振器参数下管道的临界流速的变化.从式(10)~式(12) 可以看出,减振器的线性弹簧刚度、阻尼系数、惯容系数和安装位置都可能对悬臂管的稳定性产生影响.首先,研究不同安装位置对临界流速的影响,取计算参数为α=0.001,β=0.142,γ=18.9,bf=0.2,cf=0.5 和kl=60,得到减振器安装在不同位置时临界流速的变化曲线,如图4 所示.从该图可以看出,当ξb=0 时相当于没有减振器作用,此时临界流速ucr=6.17.随着安装位置坐标ξb的增大,临界流速除端部外也都相对有所增大.在安装位置坐标ξb小于0.5 时,临界流速不断增大;当ξb在0.5~0.65 之间临界流速有所减小,但相比无减振器时还是有所增大;随着安装距离的不断增大,系统的临界流速出现明显增大,且大约在ξb=0.9 处取得最大值,此时ucr=6.84,其对应的Argand 如图5 所示.由此可见,在安装减振器时适当接近端部位置安装能显著提高管道系统的临界流速,这同时也说明不同的安装位置对系统临界流速有较大影响.
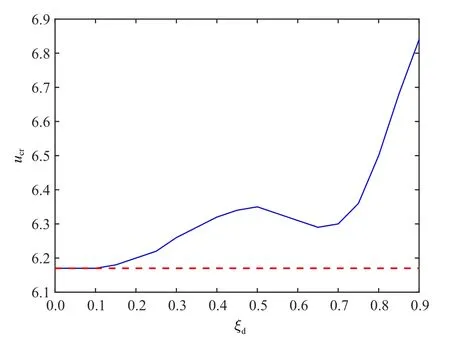
图4 临界流速随减振器安装位置变化曲线Fig.4 Variation curve of the critical flow velocity with vibration absorber installation position
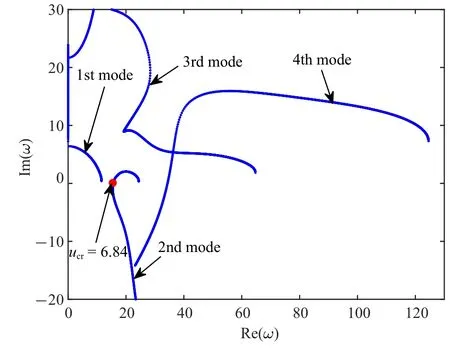
图5 安装位置在ξb=0.9 时系统的Argand 图Fig.5 Argand diagram for the pipe system when the installation position is ξb=0.9
改变减振器的惯性系数和线性弹簧刚度,得到系统的临界流速变化云图如图6 所示,显示了临界流速的逐渐演化过程.从图6(a)中可以看出,在安装位置ξb=0.3 处,当线性弹簧刚度较小时,系统的临界流速随着惯容系数的增大而增大;但当弹簧刚度较大时,随着惯容系数的增大,系统临界流速有所减小.可见不同的线性弹簧刚度会使得惯容系数对管道系统临界流速有不同的影响效果.当减振器安装位置在ξb=0.5 时,从图6(b)可以看出系统的临界流速随着惯容系数的增大而增大,但是增大弹簧刚度反而会对系统的稳定性产生消极效果,即降低临界流速.图6(c)中的结果显示,当ξb=0.7 时,随着惯容系数的增大,系统的临界流速有所减小;与此同时,线性弹簧刚度越大,则系统的临界流速越大,故其对系统的稳定性有正面作用,在弹簧刚度在55~100 区间时效果更明显.当安装位置ξb=0.9 时,从图6(d)可以看出随着弹簧刚度的增大,管道系统的临界流速先有所增大,但当弹簧刚度继续增大后临界流速有所减小,同时临界流速随着惯性系数的增大而减小.

图6 管道无量纲临界流速随惯容系数和线性弹簧系数变化云图Fig.6 Contour maps of the dimensionless critical flow velocity for the pipe changing with the inertia coefficient and linear spring coefficient
5 收敛性分析
在进行非线性动力学分析之前,有必要对Galerkin 法的模态截断问题进行收敛性分析,从而确定合适的模态截断数N.
选取管道参数α=0.001,β=0.142 和γ=18.9,将减振器安装在管道ξb=0.5 位置处,减振器各元件参数分别取为bf=0.3,cf=0.5,kl=60 及kn=8000.Galerkin 法的模态截断数N分别取为3,4 和5,得到3 种取值下管道自由端响应位移幅值的分岔图,如图7 所示.该分岔图的取点规则为:对某一给定的流速,当管道运动达到稳态后开始取点;每当管道自由端运动速度为0 时,记录该时刻管道端点处的位移数据,以此来得到管道端点位移幅值随流速变化的分岔图.从图7 可以看出:当N=3 时,管道响应的分岔图与N=4 或5 时的相差较大;当N取为4 和5时,管道响应的分岔图差异很小,因此可认为当N取4 时就已达到收敛.为减小计算量,在接下来的分析中,选取N=4 进行计算.
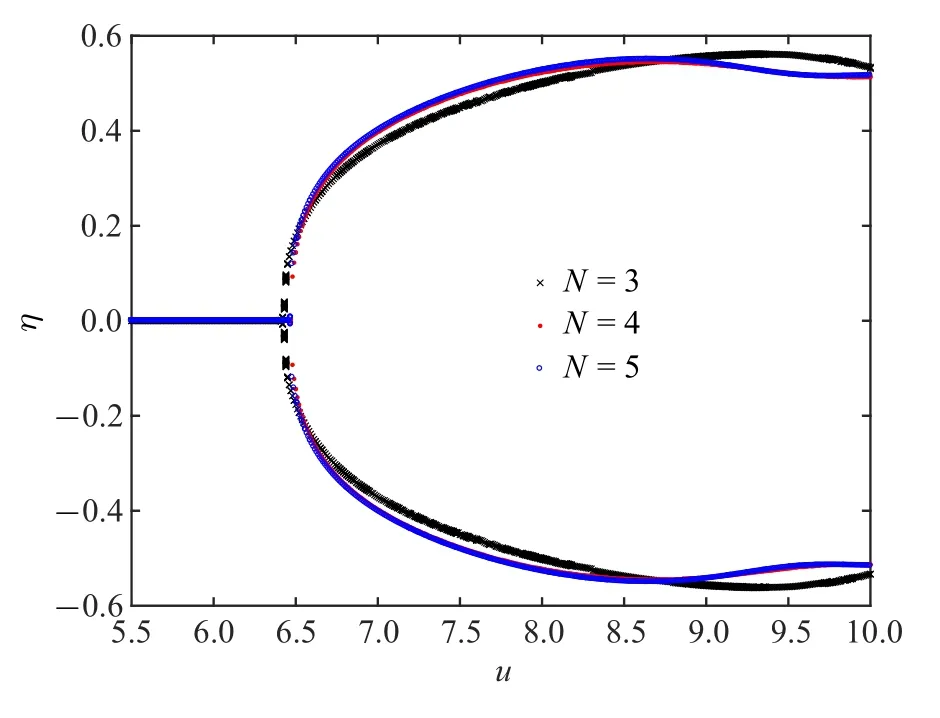
图7 不同N 时管道端部位移幅值随流速变化的分岔图Fig.7 Bifurcation diagram for the displacement amplitude of the pipe end with various flow velocities,for different N
6 非线性分析
本节研究不同流速下带有减振器的悬臂输流管道的非线性动力学行为.首先,讨论当减振器安装位置在ξb=0.5 和ξb=0.9 时惯容系数bf对管道动态响应的影响.分别选取bf=0.1,0.2 和0.3,同时固定减振器其余各参数为cf=0.5,kl=60 及kn=8000,且管道的3 个主要参数取值为α=0.001,β=0.142,γ=18.9.这些参数取值都是无量纲的,这可使得后续的计算结果更具有普遍意义.
图8 和图9 分别给出了安装位置ξb=0.5 和ξb=0.9 时不同流速下管道端部(ξ=1)的位移响应幅值,展示了管道系统在无减振器和有减振器时管道端部位移幅值随流速变化的分岔图.从图8(a) 中可以看出,当惯容系数bf=0.1 时,管道的临界流速略有增高,管道振动的振幅有所减小.随着惯容系数的增大,如图8(b)和图8(c)所示,管道系统的临界流速也会增高,同时管道振幅相较无减振器时也有所减小,这说明减振器对提高系统的稳定性有一定作用.
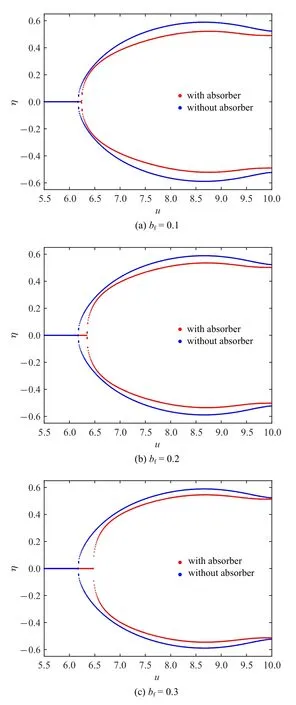
图8 ξb=0.5 时不同惯容系数下管道端部位移幅值随流速变化的分岔图Fig.8 Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities under different coefficients of inertia when ξb=0.5
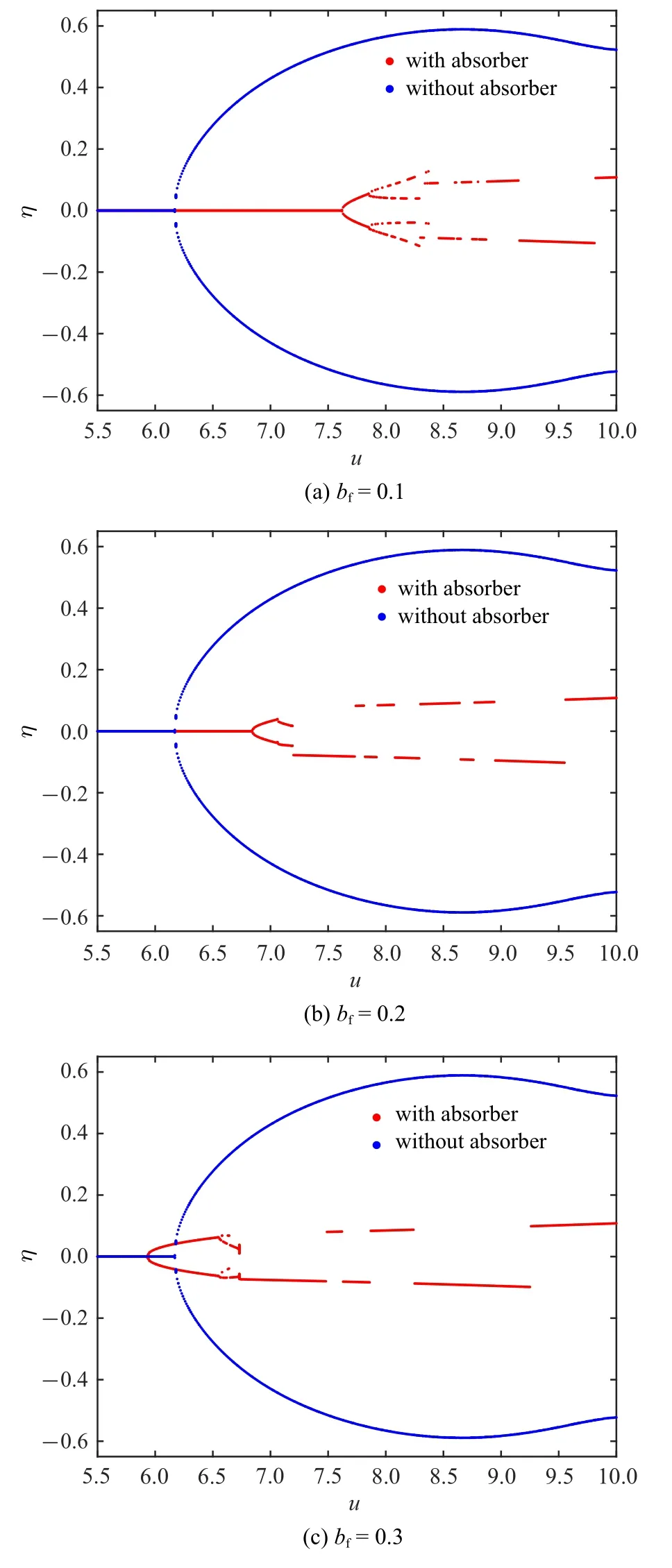
图9 ξb=0.9 时不同惯容系数下管道端部位移幅值随流速变化的分岔图Fig.9 Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities under different coefficients of inertia when ξb=0.9
图9 为安装位置在ξb=0.9 时的分岔图,当惯容系数bf=0.1 时,管道系统的临界流速有明显增大,当管道失稳振动后,管道振幅也被控制在小范围内振动,可以看出此时减振器的振动抑制效果比较显著.但是随着惯容系数的不断增大,如图9(b) 和图9(c) 所示,管道的临界流速却有所减小.对于安装位置在ξb=0.5 和ξb=0.9 时惯容系数对系统稳定性的不同影响,这说明惯容系数的增大对管道临界流速有积极作用,但却无法在所有位置产生正面的控制效果.
接下来,研究安装位置对管道非线性动力学行为的影响.为此,安装位置ξb分别取为0.3,0.5,0.7 和0.9,通过非线性计算得到不同流速下管道端部处的振动位移.数值计算时,取各系统参数值为bf=0.2,cf=0.5,kl=60 和kn=8000.从图10(a)可以看出,当ξb=0.3 时,减振器对管道振动响应幅值的影响较小,此时临界流速略有提高.关于这一点,从图4 中给出的临界流速变化曲线也可得到进一步的理解:当减振器安装位置距固定端较近时,减振器对系统的稳定性几乎没有影响.当ξb增大到0.5 时,从图8(b)可以看到,含减振器悬臂管道出现Hopf 分岔的临界流速变大,同时减振器使管道系统的振幅也有所减小.随着安装位置增大至ξb=0.7 时,从图10(b) 可以看出,临界流速相比无减振器控制时有所增大,当管道失稳后,减振器的安装对管道振动控制效果显著,明显减小了管道振动幅值.值得注意的是,当流速在[8.51,8.9]范围变化时,管道可发生黏附现象,即管道只出现静态变形.当流速继续增大时,管道振动行为可能比较复杂,分岔图中表现处较强的非线性特征,管道还出现了复杂的混沌运动现象.当ξb=0.9 时,如图9(b)所示,可以看出临界流速显著增大,同时管道发生黏附现象的流速范围变大,整个流速区间内减振器对管道振动的抑制作用都较为显著.

图10 减振器在不同位置时管道端部位移随流速变化的分岔图Fig.10 Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities when the absorber is placed at different positions
为了进一步理解ξb=0.7 时减振器对管道动态响应的影响规律,图11 给出了3 种流速下管道中点位移随时间变化的历程曲线.由该图可以看出,当流速u=6.2 时,没有安装减振器的管发产生了周期振动,而有减振器的管道却没有发生振动,这说明此时减振器提高了管道系统的稳定性.如图11(b) 所示,当流速u=7.5 时,带有减振器和无减振器的管道在内部流体的激励下都发生了周期振动,但有减振器的管道振动响应振幅相对较小,这说明减振器对管道的振动幅值有抑制作用.图12(a)显示了u=7.5 时带有减振器管道在不同时刻的振动形态,其中虚线代表该流速下某一时刻的管道振动形状,可以看到管道形态主要以第一阶模态和第二阶模态形状的成分为主.当管道流速增大到8.5 时,从图11(c)可以看到,减振器能将管道振幅控制到较小幅值,而且从图12(b)还可看到管道的振动形态有更高阶模态参与振动的迹象.
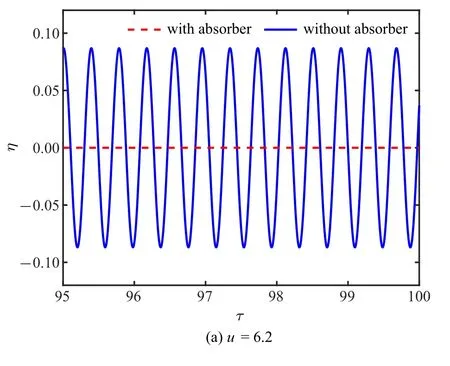
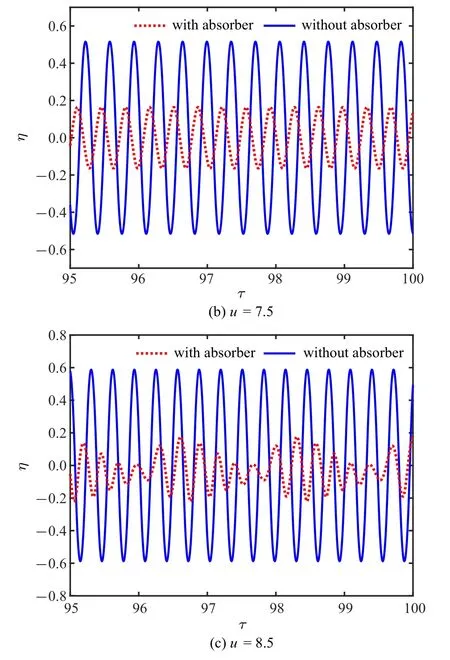
图11 ξb=0.7 时端部位移随时间变化曲线Fig.11 Displacements of the pipe end versus time when ξb=0.7
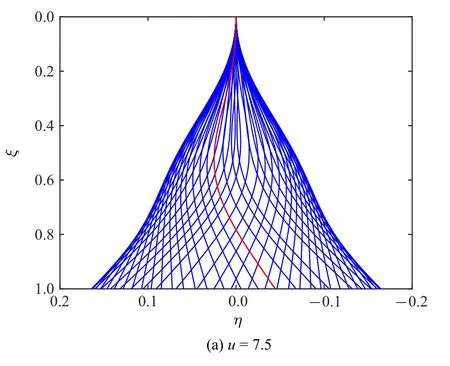
图12 ξb=0.7 时管道振动的实时形态图Fig.12 Oscillation shapes of the pipe for ξb=0.7
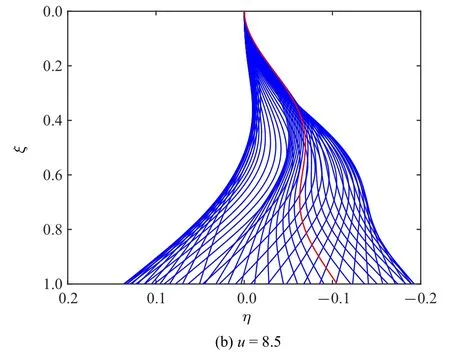
图12 ξb=0.7 时管道振动的实时形态图(续)Fig.12 Oscillation shapes of the pipe for ξb=0.7(continued)
在图10 的分岔图中,曾注意到当安装位置ξb从0.3 增大至0.7 的过程中,管道还可能诱发出混沌运动行为.图13 描述的是当减振器安装位置在ξb=0.7时管道内流速分别为7.5,8.5 和9.93 时管道端部处的振动相图曲线,该图中的横坐标和纵坐标分别表示管道中点处的振动位移和速度.由图13 可知,当管内流速u=7.5 时,管道表现为简单的周期运动.随着流速的不断增大至8.5 时,管道呈现倍周期运动.当流速继续增大至9.93 时,管道自由端振动的相轨迹如图13(c) 所示.为更清晰地判断其运动状态,图14 给出了此时管道响应位移的功率谱图和庞加莱映射图,可发现此时管道振动呈混沌状态,这种混沌响应行为是由于系统的各种非线性因素产生的.
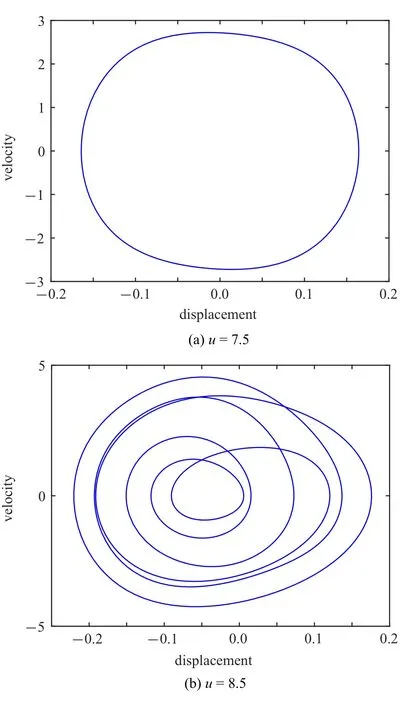
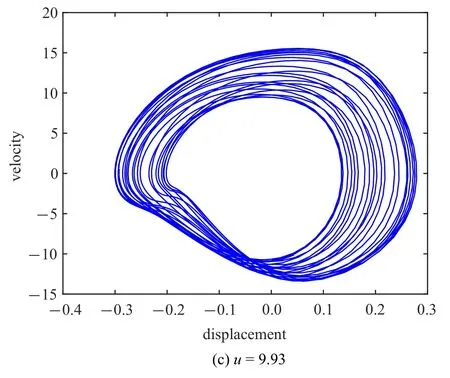
图13 ξb=0.7 时不同流速下管道端部的相轨迹图Fig.13 Phase portraits of the pipe end under different flow velocities when ξb=0.7
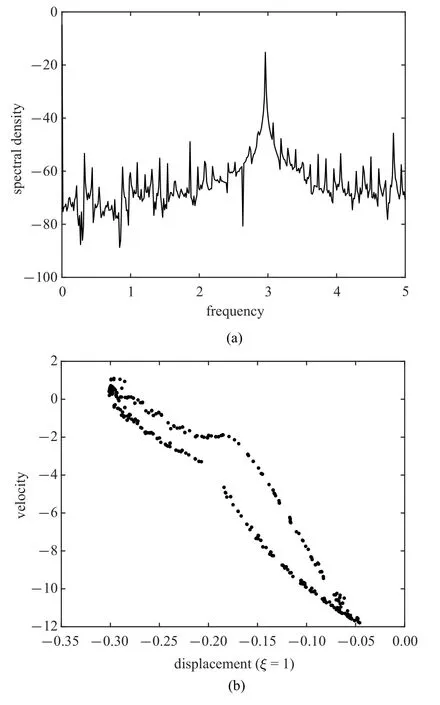
图14 在ξb=0.7 下流速为9.93 时管道响应的(a)功率谱图和(b)庞加莱映射图Fig.14 Responses of the pipe end when the flow velocity is 9.93 with ξb=0.7:(a)Power spectra diagram and(b)Poincare map
7 结论
本文基于哈密顿原理引入了含有接地惯容减振器的悬臂输流管的振动控制模型,得到了非保守悬臂管道系统的非线性运动控制方程.通过Galerkin 方法对控制方程进行离散化处理,并借助数值求解方法对含减振器悬臂管道系统的稳定性和非线性动力学行为进行了分析,探讨了不同参数下减振器在悬臂输流管振动控制中的应用效果.特别地,利用线性分析,探究了惯容系数、线性弹簧刚度和减振器安装位置对管道发生颤振失稳时临界流速的影响.利用非线性分析,还探讨了减振器对管道非线性动态行为的影响规律,揭示了含有接地惯容减振器悬臂管的周期和混沌运动等动力学行为.
对于未安装减振器的悬臂管道,当管内流速超过某一临界流值时,系统会因颤振而失去稳定性.当安装减振器后,通过调节减振器位置等参数取值,管道的颤振失稳临界流速可以得到明显的增大.通过线性分析发现,惯性系数和线性刚度对管道稳定性的影响与减振器安装位置不同而有不同的作用效果.还应指出的是,通过非线性分析发现:减振器对管道振幅的抑制效果与流速取值和减振器安装位置密切相关.在不同的流速区间,减振器不仅会使得系统的稳定性得到较大提高,还会在较大流速时会改变管道的动态响应特征,例如产生倍周期和混沌运动等.总体而言,减振器在接近管道端部位置时能使得管道系统产生较大的临界流速,在中高流速区间取值时对管道振幅有较好的抑制作用.
附录
为了应用广义Hamilton 原理,本附录给出含接地惯容器悬臂管道系统的动能、势能及非有势力做功项的具体表达式.
取悬臂管道上任意一点进行研究.管道变形时该点的位置矢量和切向矢量可分别用r和τ 表示[1]
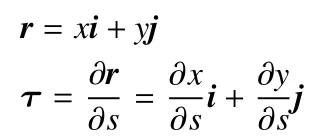
由此可得悬臂管道系统的总动能为[1]
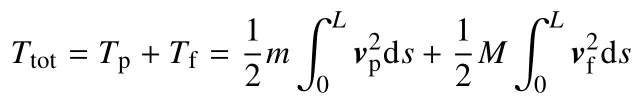
其中,vp和vf分别表示管道和流体的运动速度,可写为如下形式[1]

系统总势能包括管道的应变能、管内流体的重力势能和减振器的弹簧势能,可写成
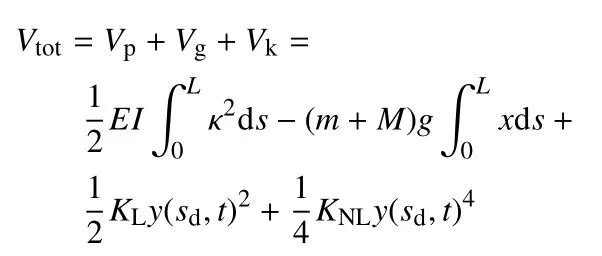
其中
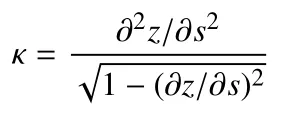
为管道轴线的曲率,y(sd,t) 表示管道在减振器安装位置处的横向位移.
系统非有势力做功包括阻尼器和惯容器所做功,可写成