基于波速衰减的混凝土损伤声发射定位优化算法试验研究

何兆益，杨 康，李冬雪，周翰林

(1. 重庆交通大学 交通运输学院，重庆 400074； 2. 重庆交通大学 土木工程学院，重庆 400074)

0 引 言

混凝土属于人工复合材料，在各种建设工程中广泛应用，其结构受载会产生损伤，且损伤不断累积会导致脆性破坏，从而影响结构正常的使用，增加安全隐患[1]，因此对混凝土的损伤破坏进行深入研究十分必要。对材料内部的细微变化进行监测、分析的技术称为声发射技术(acoustic emission, AE)，已广泛应用于岩石的动态无损健康监测中[2-5]。

针对混凝土类复合型材料，现阶段研究主要集中于利用声发射参数，如能量、振铃计数、频率、波形等对混凝土损伤破坏特征进行表征分析[6-9]，对于混凝土类材料的声发射源定位研究起步较晚，1970年才代出现相关研究[10]。

声发射源定位技术对于损伤点的准确测定起到重要作用，现有源定位算法多为时差定位法[11-13]，通过提取声发射源到达传感器的时间以及各个传感器间的距离，求解声发射源定位点坐标，即为声发射定位点，从而对材料可能出现的损伤点进行预测[14-15]。现有时差定位算法将波速的传播视为恒定值，但现有研究表明，波速的改变对定位精度影响较大[16]。对于混凝土类的人工复合型材料，波在内部传播时衰减严重，导致波速并不以恒定值传播，使得定位与实际损伤误差较大，因此探究波速在混凝土内部的衰减特性，并考虑波速的衰减，建立基于波速衰减的源定位算法，对于提高源定位精度至关重要。现阶段考虑波速衰减的定位算法研究较少，尤其是三维定位相关算法。

基于此，笔者对混凝土梁进行波速衰减试验，探究波速的衰减特性，从期得出波速随距离的传播函数公式，并得到衰减率；基于波速衰减公式，建立考虑波速衰减的声发射源三维穷举定位算法；进行三点加载试验，利用此算法对加载过程的损伤点进行三维定位，并与常用时差定位法进行对比，验证其准确性和可靠性。

1 试验材料、方法及理论

1.1 试件制备

试验制备6根100 mm×100 mm×1 800 mm水泥混凝土大梁与3根100 mm×100 mm×400 mm水泥混凝土小梁，水泥为42.5普通硅酸盐水泥，粗骨料为粒径5～20 mm石灰岩碎石，配合比如表1。采用机械拌合，振动台振捣，标准养护室养护28 d，大梁编号D1～D6，小梁编号T1～T3，成型试件如图1。

图1 试验试件Fig. 1 Test specimens

表1 混凝土试件配合比Table 1 Mix proportion of concrete specimen

1.2 波速衰减试验

选D1～D6进行波速衰减试验，为探究波速在混凝土内部随距离的衰减特征，采用声华SEAU3H型16通道声发射采集仪，选取SR150S型传感器，频率接受范围为70～280 kHz，传感器呈线性布设于试件上表面。试验中前置放大器设置为40 dB，门槛阈值设置为35 dB，采样频率为1MHz。试验步骤如下：

步骤1传感器安装：使用耦合剂将传感器线性布设在试件表面，各传感器间距100 mm，如图2；

图2 波速衰减测试Fig. 2 Wave velocity attenuation test

步骤2传感器调试：在每个传感器附近断铅3次，验证其耦合条件与接收性能；

步骤3断铅试验：在1#传感器处进行五次断铅试验模拟标准声发射信号，每次断铅间隔2 s，确保所有传感器均成功接收信号；

步骤4移至下一试件，直至试验完成。

1.3 三点加载试验

先T1～T3进行三点加载试验，试验荷载控制采用万能压力机，输出最大压力1 000 kN，可实现控制恒定位移进行加载。试验保持0.1 mm/min的加载速率，试验耗时约15 min，加载系统全程记录荷载-位移曲线。采用SAEU3H声发射信号采集系统，研究采用8通道采集。

试验声发射参数设定为：阈值45 dB，采样速率1 MHz，传感器型号为SR150S，频率接受范围为70～280 kHz。传感器①～⑧坐标分变为(150,0,0)、(250,0,0)、(250,100,0)、(150,100,0)、(150,0,100)、(250,0,100)、(250,100,100)、(150,100,100) ，布设方式如图3。

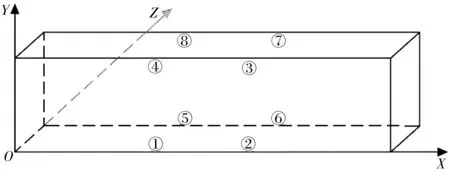
图3 传感器布设Fig. 3 Layout of sensors

1.4 试验理论

1.4.1 波速衰减

声发射标准信号在材料内部传播时受各种影响因素会产生衰减，而距离对其影响最为显著[16]，因此笔者对波速的衰减进行测试(如图2)，根据波速衰减试验原理，波速随距离的传播计算如式(1)：

(1)

式中：Δdi，i+1为相邻两传感器间距；Δti，i+1为纵波到达相邻两传感器时间差，由传感器测得。

将计算的各个波速进行拟合，得到波速随距离的衰减函数Vm。

1.4.2 基于波速衰减的声发射源定位算法

基于波速衰减特性以及波速衰减试验得到的衰减函数Vm，采用穷举法作为声发射源定位方法，并改变原有时差定位算法中采用恒定波速的计算方式，以此提高三维声发射源定位点的精度与准确性。

在三点加载试验中，设声发射源在材料内部传播至1#～4#传感器的示意如图4，声发射源距第i个接收信号的传感器的距离di如式(2)：

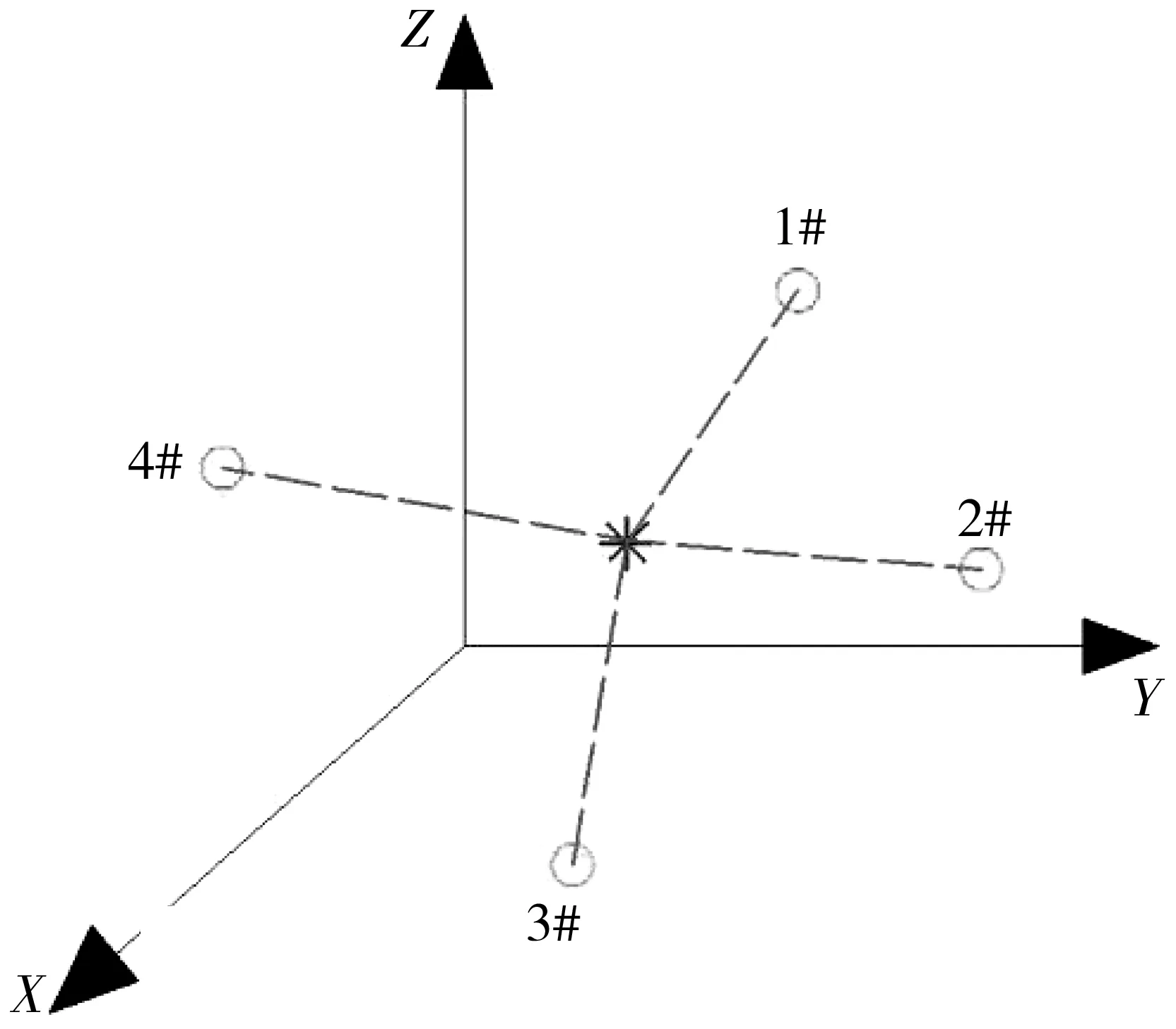
图4 声发射源三维定位示意Fig. 4 Three-dimensional positioning of AE source

(2)

式中：(x，y，z)为声发射源坐标；(xi，yi，zi)为第i个接收信号的传感器坐标。

根据波速的拟合公式，可得声发射源传播至第i个接收信号传感器的理论时间值Ti如式(3)：

(3)

已知试验实测声发射源传播至第1个与第i个接收信号传感器的实测时间值分别为t1与ti，则第一个与第i个接收信号传感器时差的理论值与实测值为ΔT1i与Δt1i，理论值与实验值之间的误差e1i为：

e1i=ΔT1i-Δt1i

(4)

对于理想均质材料，e1i=0，由于试验误差使得e1i≠0，因此引入最小二乘法思想，对各部分误差求平方和e：

(5)

笔者采用穷举法，将混凝土试件3个坐标轴方向按等网格进行划分，网格相交产生大量格栅，将格栅点的坐标依次代入式(5)，求得使式(5)取的最小值时的网格值坐标(x，y，z)，理论上，此时的网格值为声发射源坐标。

2 试验结果

2.1 波速衰减试验

图5为波速衰减测试过程中，断铅信号传播至传感器所接收到的声发射信号衰减波形，其中传感器取图2中的1#～3#。

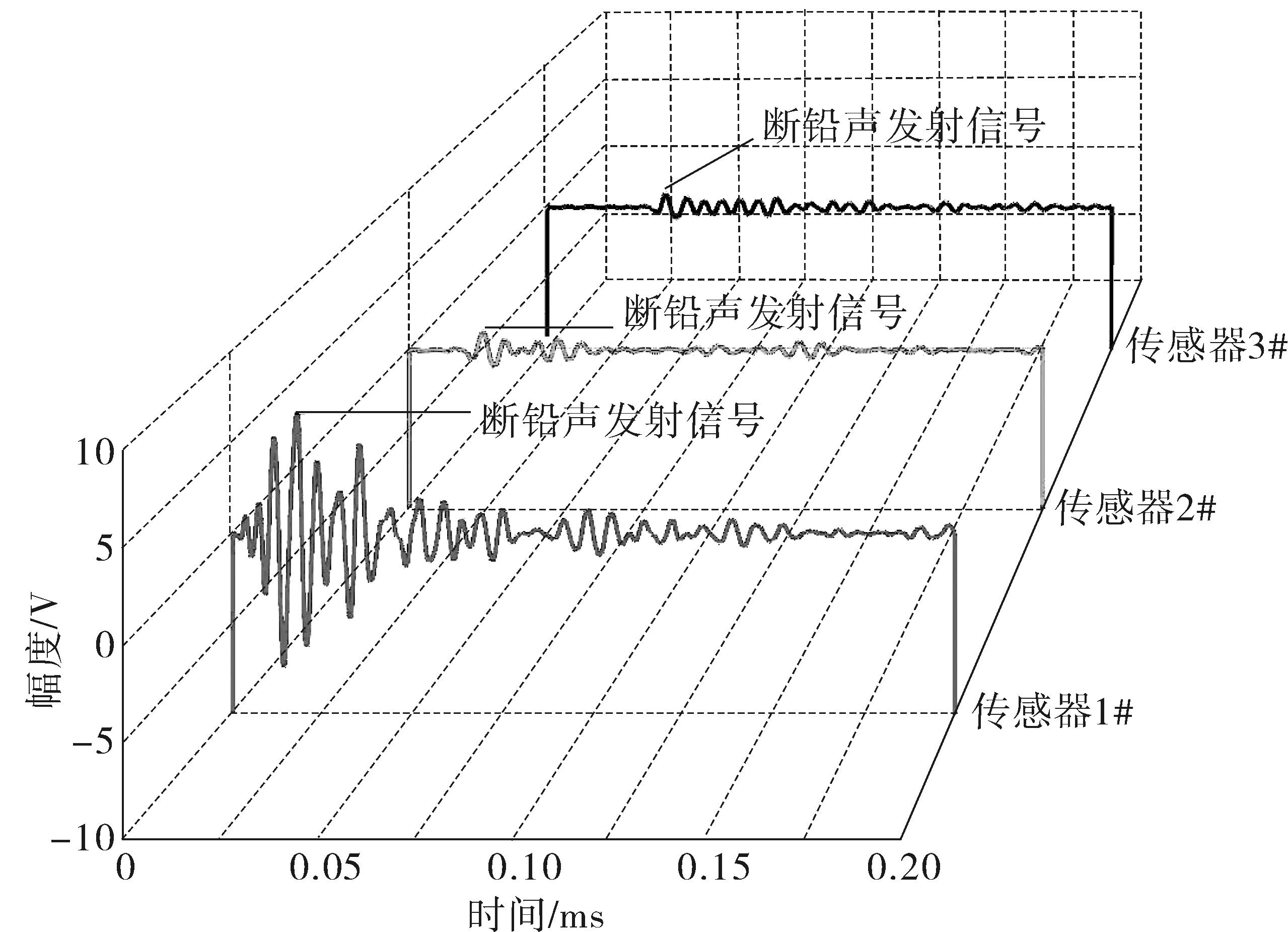
图5 传感器1#～3#采集断铅波形Fig. 5 PLB waveform of sensor 1～3

由式(1)计算得到波速随距离的变化值如图6所示，可以看出波速随距离的衰减现象较为严重，初始的基准速度为4 745 m/s，在传播600 mm时已降至2 124 m/s，衰减率达到55%，距离在600～1 000 mm 内逐渐趋于稳定，整体呈现非线性衰减。

2.1.3 供试品溶液的制备 取本品粉末（过4号筛）约0.3 g，精密称定，置具塞锥形瓶中，精密加甲醇50 mL，密塞，摇匀，称定质量，放置过夜，超声处理（功率250 W，频率50 kHz）30 min，取出，放冷，再称定质量，用甲醇补足减失的质量，摇匀，滤过，取续滤液，过微孔滤膜，得到供试品溶液。

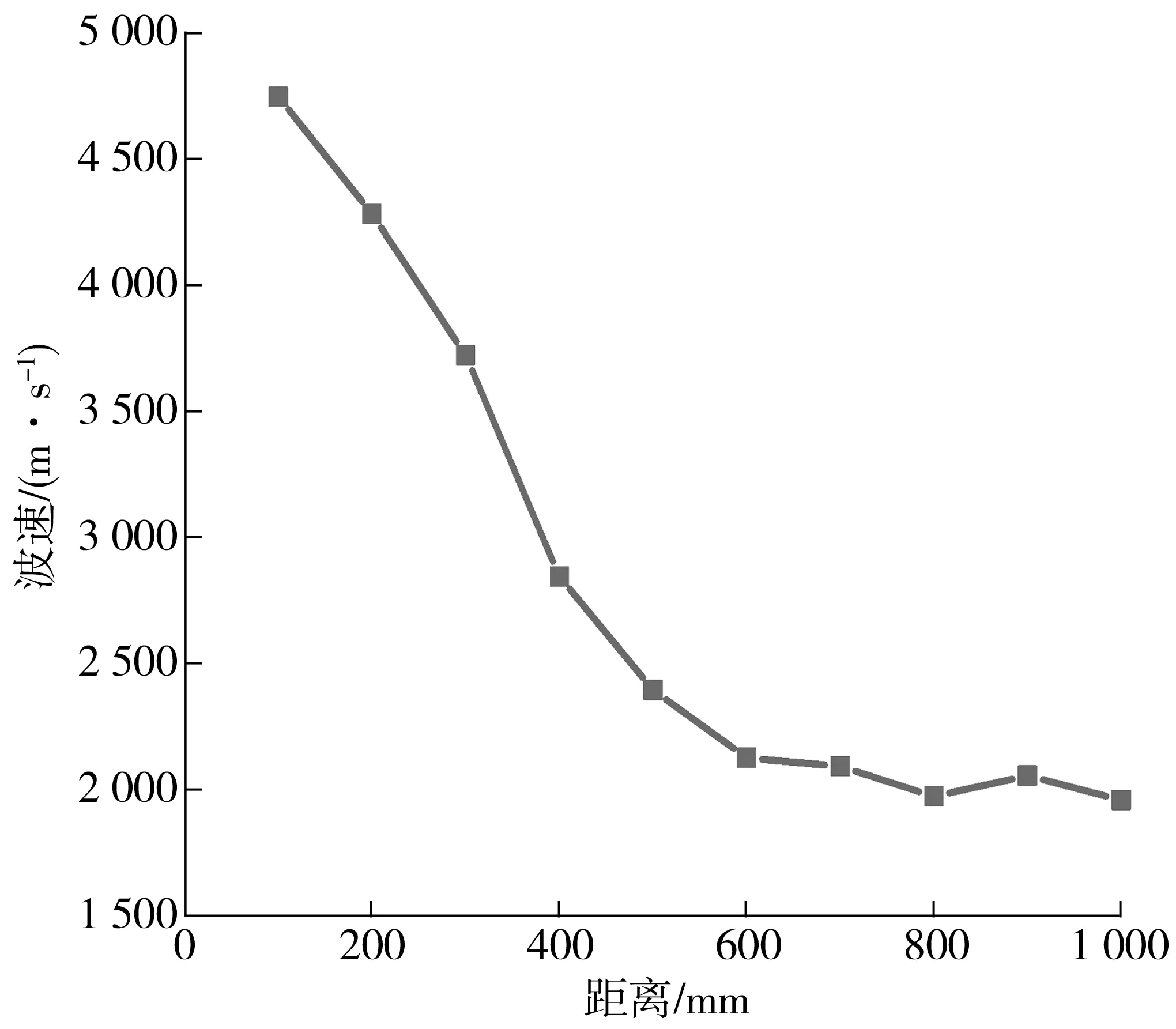
图6 声发射波速衰减Fig. 6 AE wave velocity attenuation

将波速进行多项式拟合，得出波速Vm随距离x的拟合函数，如图7。

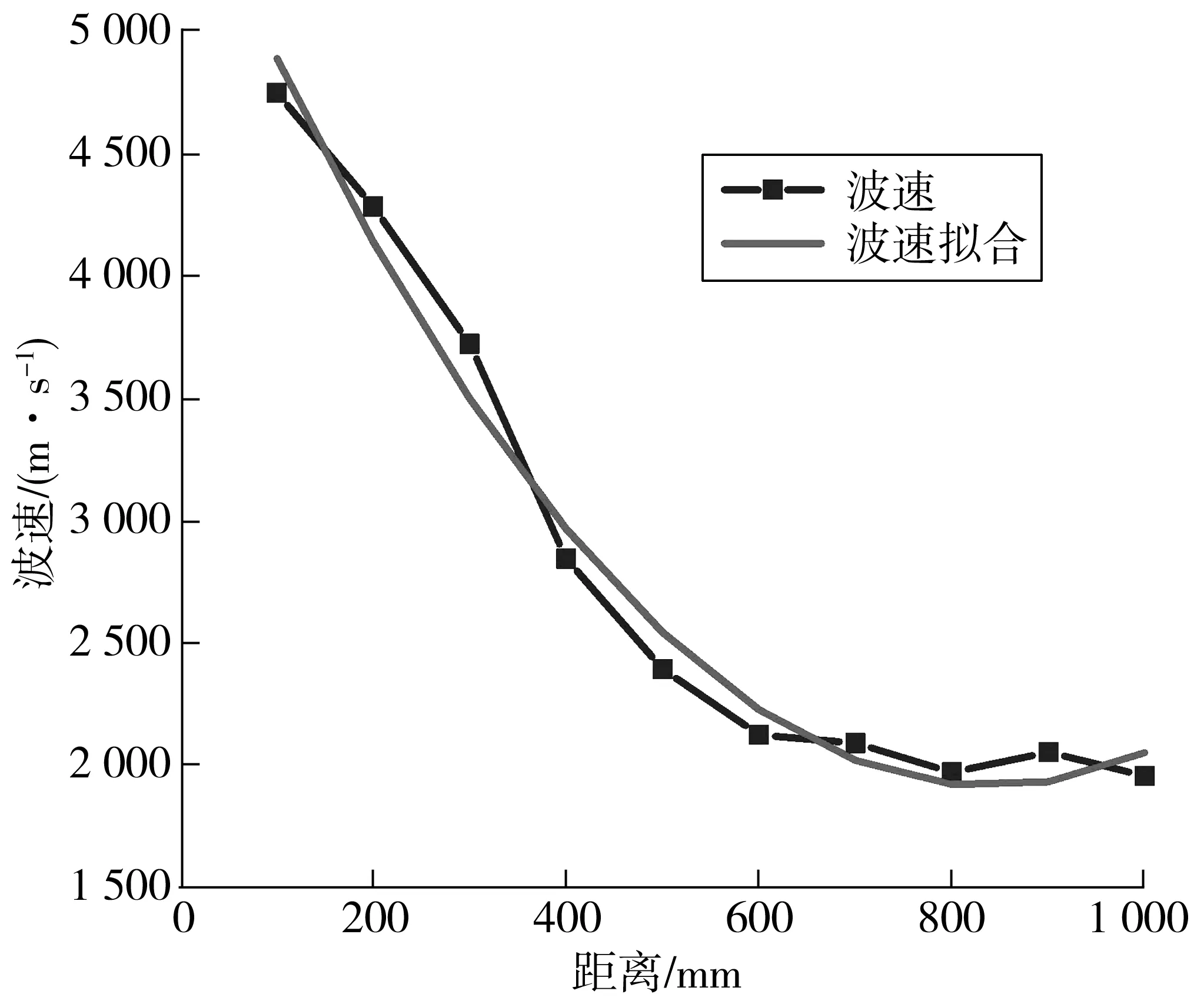
图7 波速衰减拟合函数Fig. 7 Wave velocity attenuation fitting function

拟合函数如式(9)：

Vm=5 743.13=9.12x+0.005 4x2

(9)

2.2 三点加载试验

试件损坏后裂缝的延展如图8(a)，由图可知对于未预设切口的小梁试件，起裂点均在中线附近，其裂缝延展方向具有随机性，形状为不规则曲线，试验中T1～T3号试件试验结果具有一致性，笔者取T3进行分析，由图8(b)可知，T3的裂缝周围形成明显的断裂带，经测量其正面断裂带范围为3 cm×10 cm的矩形。

图8 试件损坏情况Fig. 8 Test piece damage condition

图9为T3的荷载-位移曲线，整个曲线可分为4个阶段：

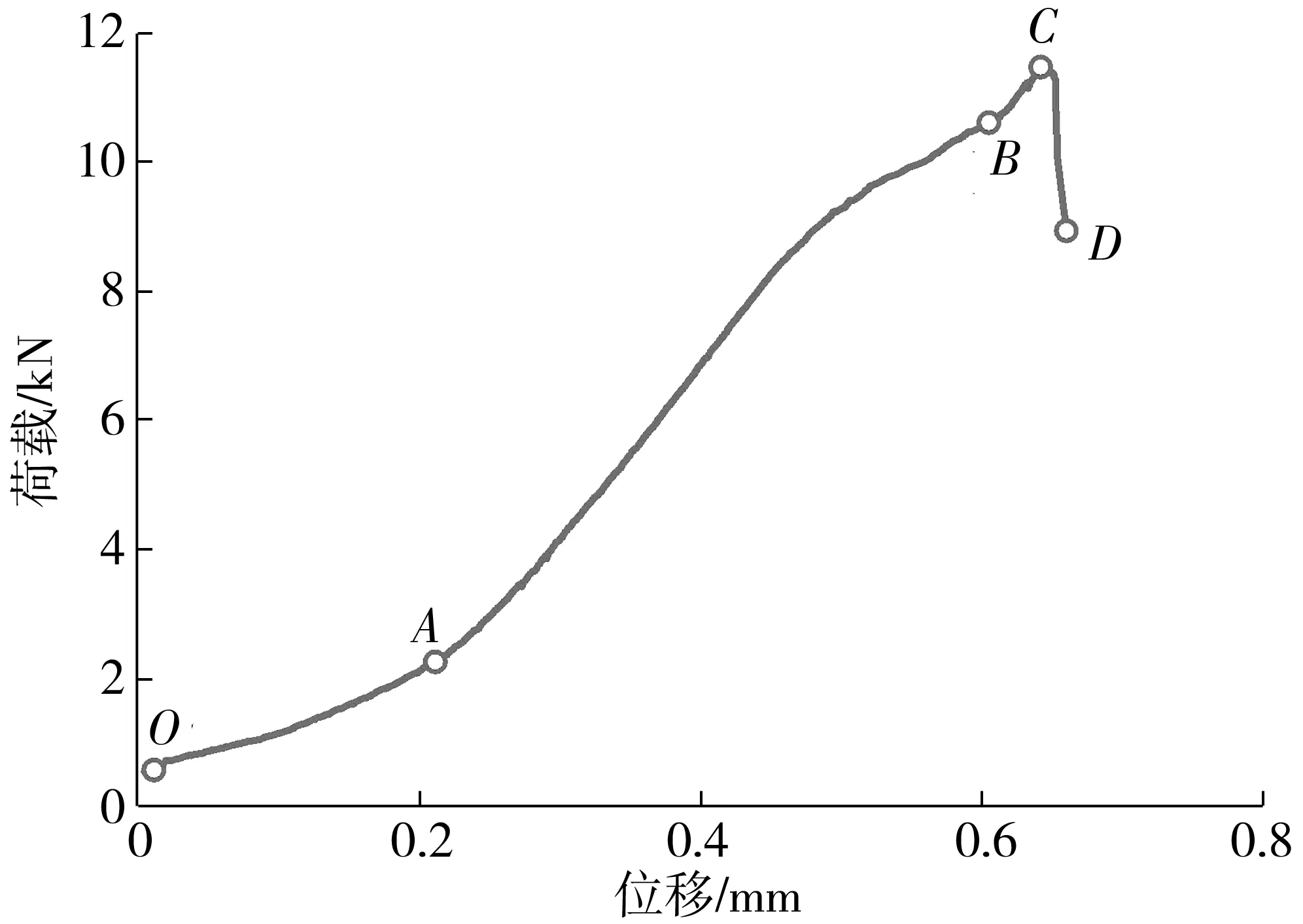
图9 荷载-位移曲线(T3)Fig. 9 Load-displacement curve (T3)

OA段(初始压密)：此阶段位移元件开始接触试件表面，荷载上升较为缓慢，不超过极限荷载的20%，此时位移主要来自试件表面压陷。

AB段(弹性变形)：此阶段荷载上升速率明显增大，达到极限荷载的90%，试件产生弹性形变，位移来自试件的受力弯曲。

BC段(塑性变形)：此阶段荷载迅速上升，达到试件抗弯荷载极限值，试件产生不可逆的塑性变形。

3 源定位算法结果

3.1 优化算法定位结果

按照试件受载特性，将声发射源定位点按时域划分为4阶段，分别为第250、350(B)、375(C)、380 s(D)点，其中B、C、D点与图9一致。穷举法计算中，网格划分越多，格栅点越多，定位精度会有显著提升，但过多网格会导致工作量过大，耗时太久。在保证定位精度的基础上减少工作量，将网格以1 mm为单位进行划分计算。

为探究优化后源定位方法的准确性，将原有时差定位损伤点和优化后的定位损伤点结果，与实际损伤裂缝的扩展路径进行对比，并用不同符号表示，圆圈形为时差定位损伤点，十字叉为优化后的定位损伤点，结果如图10。

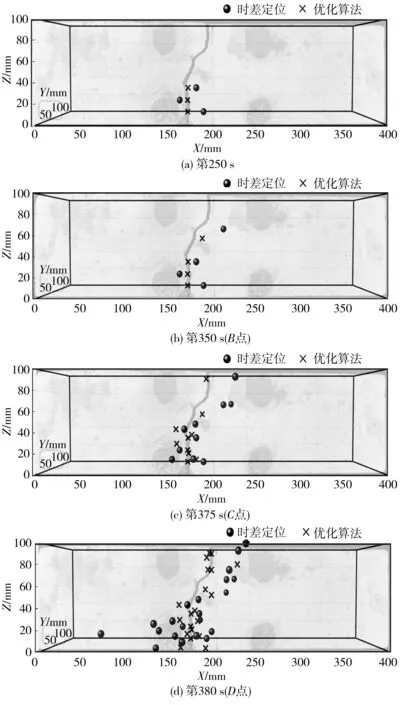
图10 定位损伤点对比Fig. 10 Comparison of locating damage points

由图10可知，将2种算法与实际裂纹进行对比，在弹性变形阶段初期，即图10(a)的0～250 s，2种算法的损伤点均出现在试件底部的受拉区，在图10(b)的弹性阶段后期，即250～350 s之间，在受压区域出现1处损伤点，但优化算法明显更接近实际裂纹；

由图10(c)可知，BC点之间的塑性变形阶段，即350～375 s之间，2种算法的损伤点均不同程度的向试件中心的受压区扩展，原有算法在受压区新增2处损伤点，多于优化算法的1处，而优化算法更接近实际裂纹的扩展路径，优化算法新增定位点更多的集中在受拉区。

由图10(d)可知，荷载到达C点之后，即375～380 s之间，2种算法的受压区与受拉区损伤点数目均迅速增加，并且均集中在宏观裂缝附近，而优化算法的损伤定位点更接近实际裂纹的扩展路径，尤其是试件上部的损伤点。所有损伤点在裂缝的扩展路径周围形成明显的断裂带。

3.2 优化算法定位精度

将裂缝路径周围区域视为断裂带，通过测量得到断裂带在平面区域范围为X：169～197 mm，Z：0～100 mm，如图9。将所有源定位点在XZ平面进行投影，计算此断裂带内所有源定位点，如表2。

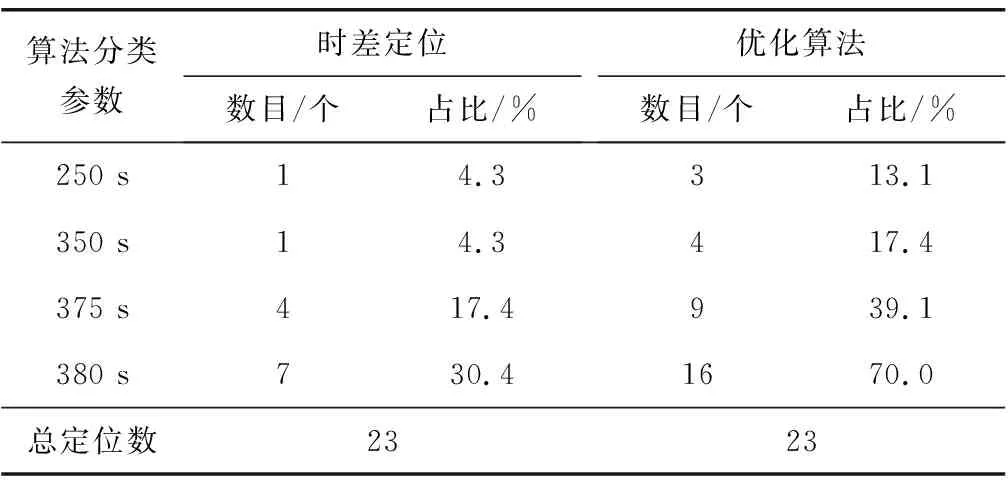
表2 断裂带内源定位点Table 2 Endogenous location of fault zone

由表2可知，试验全程定位点共23个，所有定位点中，优化算法在断裂带范围内有16个定位点，占比70.0%，而时差定位法在断裂带范围内只有7个，占比30.4%，定位精度明显高于时差定位法；

其中在弹性变形阶段，即350 s之前，优化算法的定位点数量高于时差定位法，表明优化后的算法对于混凝土的起裂点预测的准确性高于时差定位法。

在荷载接近试件抗弯极限，发生脆性断裂前后(350～380 s)，优化算法定位点在断裂带内的数量由4个上升至16个，占比由17.4%上升至70.0%，明显多于时差定位的涨幅，表明优化算法对于混凝土的脆性断裂带的预测效果明显优于时差定位法。

4 结 论

1)标准声发射信号波速与距离曲线呈非线性，波速在混凝土内部随距离增大衰减现象较为严重，初始的基准速度为4 745 m/s，在传播600 mm时已降至2 124 m/s，衰减率达到55%。

2)时差定位法与优化穷举法均可以从宏观上反映混凝土裂缝的扩展趋势，但优化穷举法定位点更接近实际裂缝的延展路径，其所有损伤点在裂缝的扩展路径周围形成明显的断裂带。

3)优化穷举法定位精度明显高于时差定位法，其对起裂点有较为准确的预测作用，并且在混凝土梁的脆性断裂阶段，断裂带内的优化穷举法定位点数量由4个上升至16个，占比由17.4%上升至70.0%，明显高于时差定位法。