钢管混凝土劲性骨架拱桥混凝土外包过程非线性屈曲分析
2021-11-09郭增伟周水兴
郭增伟,程 皓,周水兴
(重庆交通大学 土木工程学院, 重庆 400074)
0 引 言
混凝土拱桥因为自身刚度高、耐用性好、造价低、外形美观等优点,在300~500 m跨径范围内具有很强的竞争力,但施工技术是大跨混凝土拱桥跨径突破的重要限制因素。20世纪90年代,我国将钢管或型钢拱架作为混凝土外包的支架及模板,开创了劲性骨架拱桥的新型结构[1],并成功修建了当时世界上最大跨径的钢筋混凝土拱桥——主跨420 m的万州长江大桥。利用劲性骨架外包混凝土的施工方法,有效解决了大跨径混凝土拱桥施工支架问题,目前全世界跨径超过300 m的钢筋混凝土拱桥仅有13座,位于我国的9座均为劲性骨架拱桥[2]。外包混凝土一般采用分段、分环方式现场浇筑[3],每环混凝土合龙结硬后才会与劲性骨架联合,承受后面浇筑的各环混凝土重量,在每环混凝土纵向合龙前,劲性骨架和已合龙结硬的混凝土是未合龙混凝土的主体承重结构,此时结构刚度较小但荷载相对较大,结构稳定问题最为突出,如何保证每环混凝土合龙前结构的稳定,是保证劲性骨架拱桥安全施工的关键问题之一。
目前国内外学者已对劲性骨架拱桥施工过程中结构稳定性开展了一些研究,LUO Kai等[4]研究了承受中心集中载荷的CFST圆拱的长期面内结构行为和稳定性,发现了非线性分析所预测的位移和内力的长期增加远大于线性分析所预测的,指出需要进行非线性分析来评估拱桥在长期荷载作用下的稳定性极限承载力;顾安邦等[5]指出劲性骨架拱桥结构稳定分析中,弦杆达到极限承载力退出工作后可使整体稳定安全系数降低15%~25%;王业飞等[6]采用Ansys模拟了劲性骨架拱桥混凝土箱形截面的分次浇筑过程,研究发现风荷载对混凝土外包阶段稳定系数的影响较大,需要通过增设临时横撑提高施工稳定性;L.XU等[7]指出,正确的浇筑混凝土步骤有助于提高CFTS拱桥在施工过程中的横向稳定性;J.WANG 等[8]比较了几何非线性和材料非线性对主拱稳定性的影响效应,认为主拱的几何非线性效应不明显,引起结构失稳的主要因素是材料非线性;陆新民等[9]则认为混凝土板在施工过程中的应力处于弹性工作阶段,在施工阶段的稳定性分析中可以不考虑材料非线性,主拱的非线性主要表现在几何非线性上;两个不同的结论说明对于不同的拱桥,非线性的表现方式可能不同;Y.GENG等[10]研究CFTS拱稳定性时考虑了核心混凝土的蠕变屈曲行为,指出由于时间效应引起的预屈曲变形,拱的极限承载力可降低多达18%。目前研究发现并明确了劲性骨架拱桥施工过程中的一些薄弱环节,并给出了相应的改进措施,为保障施安全提出了指导性依据。劲性骨架拱桥外包混凝土过程中,每环混凝土合龙前后承重结构体系不尽相同,未被混凝土包住的钢骨架构件的内力,比用混凝土包住后受力的钢构件的内力大得多,很可能结构在丧失整体稳定之前,已发生局部构件失稳。目前国内学者对劲性骨架拱桥混凝土外包过程中骨架构件局部失稳研究较少,在非线性屈曲分析中,可能疏忽了结构整体失稳掩盖的局部构件的先期失稳。
笔者以某主跨为600 m的劲性骨架拱桥为研究对象,在进行劲性骨架拱桥混凝土外包施工阶段的非线性屈曲分析中,除追踪结构整体失稳的受力历程外,对局部构件的变形情况同时进行考虑,发现施工过程中可能发生的局部失稳现象并对失稳原因进行分析,结合失稳原因给出了相应改进措施。
1 双重非线性屈曲的有限元分析
1.1 非线性屈曲分析的有限元方法
拱结构非线性主要表现为几何非线性和材料非线性:几何非线性是计入结构几何变形引起整体刚度变化,以及单元形状的改变及单元方向的改变引起的单元刚度的变化的非线性问题;材料非线性是材料在承受屈服极限应力后表现出的非线性性质。非线性屈曲分析就是考虑几何或材料非线性,或者同时考虑几何和材料非线性的一种非线性静力分析。结构的稳定极限承载力分析考虑的非线性破坏历程如图1。在弹性阶段加载时,结构的荷载与变形呈线性关系,结构保持一种平衡状态;随着荷载的增加,结构的变形和应力不断增加,结构变形加快;当荷载达到峰值时,荷载增加很少甚至不再增加,结构也会发生很大的变形,最终发生失稳破坏。这个荷载峰值就是结构的失稳荷载,据此,笔者定义结构稳定性系数(安全系数)K的含义如式(1)。
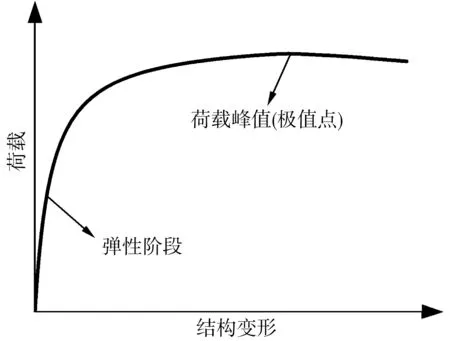
图1 结构非线性分析破坏历程Fig. 1 Failure process of structure nonlinear analysis
Pcr=K(Pbi+Pq)
(1)
式中:Pcr为结构极限承载力;Pbi为结构初始状态受到的恒载;Pq为结构初始状态受到的活载。
针对钢管混凝土劲性骨架拱桥的非线性屈曲分析,笔者采用ANSYS有限元分析软件求解。ANSYS非线性屈曲分析中,几何非线性通过打开大变形开关NlGeom激活大变形效应实现,材料非线性通过定义材料非线性本构关系模型实现。在非线性屈曲分析前,先要对理想结构进行特征值分析(弹性屈曲分析),特征值分析结果将用于指导非线性屈曲分析。特征值分析的结构屈曲模态主要有2个作用:①用于寻找非线性分析中绘制荷载位移曲线的关键节点;②作为初始缺陷的形状施加在原模型上,得到带有初始缺陷的非理想结构。特征值系数用于估计结构非线性屈曲分析求解的临界荷载。非线性屈曲分析时,将结构受力全过程荷载分为有限个荷载增量,假定每级荷载下的结构刚度为常量,采用弧长法[11]迭代计算每级荷载下的解。结构稳定性系数通过绘制结构的荷载-位移曲线求得。
1.2 钢管混凝土的ANSYS模拟及材料本构模型
对于钢管混凝土劲性骨架混凝土拱桥,钢管混凝土的模拟对非线性屈曲分析的准确性至关重要,ANSYS中常用的钢管混凝土单元建模方法为基于统一理论的钢管混凝土法和双单元法[12]。统一理论法将钢管和混凝土进行统一,视为一种组合材料,并以大量的实验为基础进行回归分析,得到钢管混凝土统一本构关系。其局限性是只适合于轴心受压构件,对于拱桥弦管这种处于弯剪扭等复杂受力状态下的本构关系,目前尚无统一的本构关系[13]。双单元法即分别定义钢管和核心混凝土的材料特性,以共节点方式分别连接钢管及混凝土单元,从而保证两种单元位移相同并且能够共同受力。在弹性受力时,双单元法能给出精确的动静力有限元计算结果,进入非线性阶段后,由于双单元法忽略了钢与混凝土间的三向约束作用,通常给出偏于保守的结果。笔者在研究中采用双单元法来模拟钢管混凝土材料。
双重非线性屈曲分析需要引入材料非线性本构关系,对于钢管混凝土结构而言,计算结果的准确性依赖于构件材料本构关系的合理性。研究中钢管混凝土弦管采用双单元法建模,需要分别定义钢管钢材和混凝土材料的本构模型。对于混凝土材料,Hognestad模型能较好反映混凝土受压时基本特征,其曲线方程形式被多国混凝土设计规范所采用。虽然该模型没有考虑到钢管的套箍作用对核心混凝土强度的提高,但对于结构材料非线性计算的结果是偏安全的,模型曲线方程如式(2):
(2)
式中:σcu、ε分别为混凝土的应力和应变;ε0为峰值应变,取ε0=0.002;混凝土标号为C60时k=0.833,混凝土标号为C80时k=0.875;fcu,k为混凝土立方体抗压强度[14]。
钢材的单轴应力-应变曲线包含线弹性阶段、屈服阶段(失去抵抗变形的能力)、强化阶段(恢复抵抗变形的能力)和二次塑流阶段共4阶段。为简化分析,常采用理想弹塑性假定来考虑钢材的本构关系,但在偏心受压的钢管混凝土柱中,钢管的应变可能会进入强化和二次塑流阶段,钢材采用理想弹塑性材料的计算结果在受力后期可能产生太过偏于保守的偏差[15]。因此,笔者使用文献[16]给出的四折线简化本构模型:
(3)
式中:Em为钢材弹性阶段的弹性模量;ε0分别为弹性极限应变;取屈服极限应变ε1=10ε0;取强化极限应变ε2=100ε0;fm为钢材的屈服强度;取钢材极限强度fu=1.6fm。
1.3 非线性屈曲分析计算准确性验证
文献[17]以一座跨径为7.5 m的单圆管钢管混凝土肋拱为对象,通过全过程缩尺物理实验和有限元数值仿真,研究了钢管混凝土拱肋的非线性屈曲行为,该拱肋拱轴线采用二次抛物线y=-4fx2/L2,净矢高f=1.5 m,拱肋使用直径121 mm、壁厚 4.5 mm的直缝钢管并内填混凝土制作。加载方案为:在模型各6分点截面施加竖向荷载P,并在拱顶截面施加0.1P的侧向荷载。采用笔者的本构模型与非线性屈曲分析方法计算得到的荷载位移曲线如图2,作为对比图2还给出了文献[17]的计算结果。
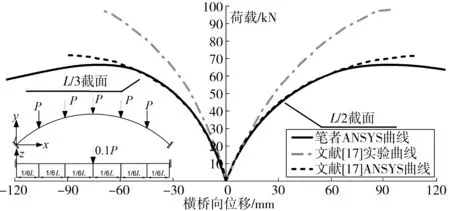
图2 单圆管拱肋荷载-位移曲线Fig. 2 Load-displacement curve of single circular tube arch rib
由图2可知:笔者分析得到的极限荷载为68.2 kN,与文献[17]计算的极限荷载71.9 kN基本一致,但与实验结果的97.1 kN相差较大,只有实验结果的70.2%。其原因可能是因为ANSYS方法中的应力-应变关系没有考虑钢管套箍作用对核心混凝土强度的提高作用,单圆管拱受力后期的抗弯刚度和强度较实际偏低,所以低估了单圆管拱的承载力。为此,采用文献[18]中考虑套箍作用的核心混凝土本构关系,对该模型再次进行了计算,结果如图3。由图3可见:考虑钢管对核心混凝土的套箍作用后极限荷载为70.2 kN,与实验结果偏差依旧较大,说明核心混凝土的本构关系不是引起这种偏差的主要原因。
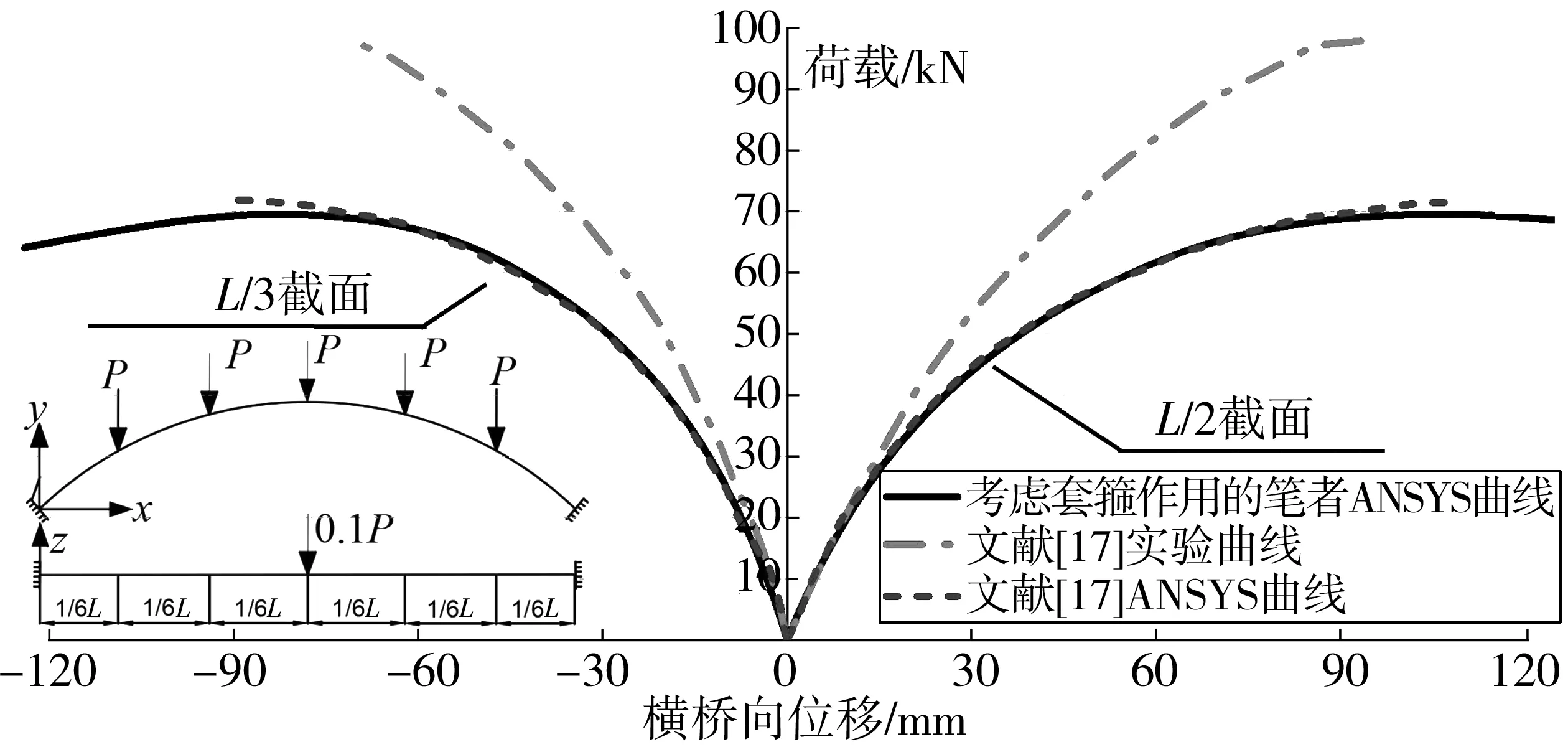
图3 单圆管拱肋荷载-位移曲线Fig. 3 Load-displacement curve of single circular tube arch rib
文献[17]中的拱为单圆管拱肋,单圆管拱肋的横向抗弯刚度较小,在面外荷载的作用下受到弯扭复合作用影响较大。而模型试验中,拱肋拱脚处面外约束(特别是转动约束)很难实现理论意义上的完全固结,这必然与数值计算中边界条件存在差异,由此造成单圆管拱肋的模型实验和数值计算中结构整体面外刚度和扭转刚度差异,进而导致受力后期ANSYS计算方法与实验曲线存在偏差。
实际桥梁工程中,大跨度劲性骨架拱桥一般为带有横撑的多肋拱,拱肋之间通过横撑连接为一个整体,在面外力的作用下,双肋组成的面外抗弯刚度和抗扭刚度远大于单肋拱,拱脚的面外转动约束相对更强。针对该类桥梁,运用笔者计算方法可能得到更为准确的结果,因此笔者进行了与文献[19]X型双肋拱实验的计算对比。
文献[19]中的模型拱拱轴线采用拱轴线系数m=1.167的悬链线,设计跨径为6.0 m,矢高f=1.5 m,矢跨比为1/4,拱肋采用直径82 mm、壁厚4 mm的钢管,内填C40混凝土;拱顶宽跨比为1/40,拱脚宽跨比为1/20;横撑均匀分布在沿跨度的5个六分点,采用直径60 mm、壁厚4 mm的钢管。加载方案为在模型各6分点截面同步施加大小为P的竖向荷载P和0.1P的侧向荷载。采用笔者计算方法的荷载位移曲线与文献[19]的结果对比如图4。由图4可见,笔者分析得到的极限荷载为139.2 kN,相当于实验结果163.0 kN的85.3%,相对于单圆管拱肋的分析更贴近实际的结果。因此,对于该类带有横撑的多肋拱桥,采用笔者方法可相对准确、保守地评估该类拱桥的稳定极限承载力。
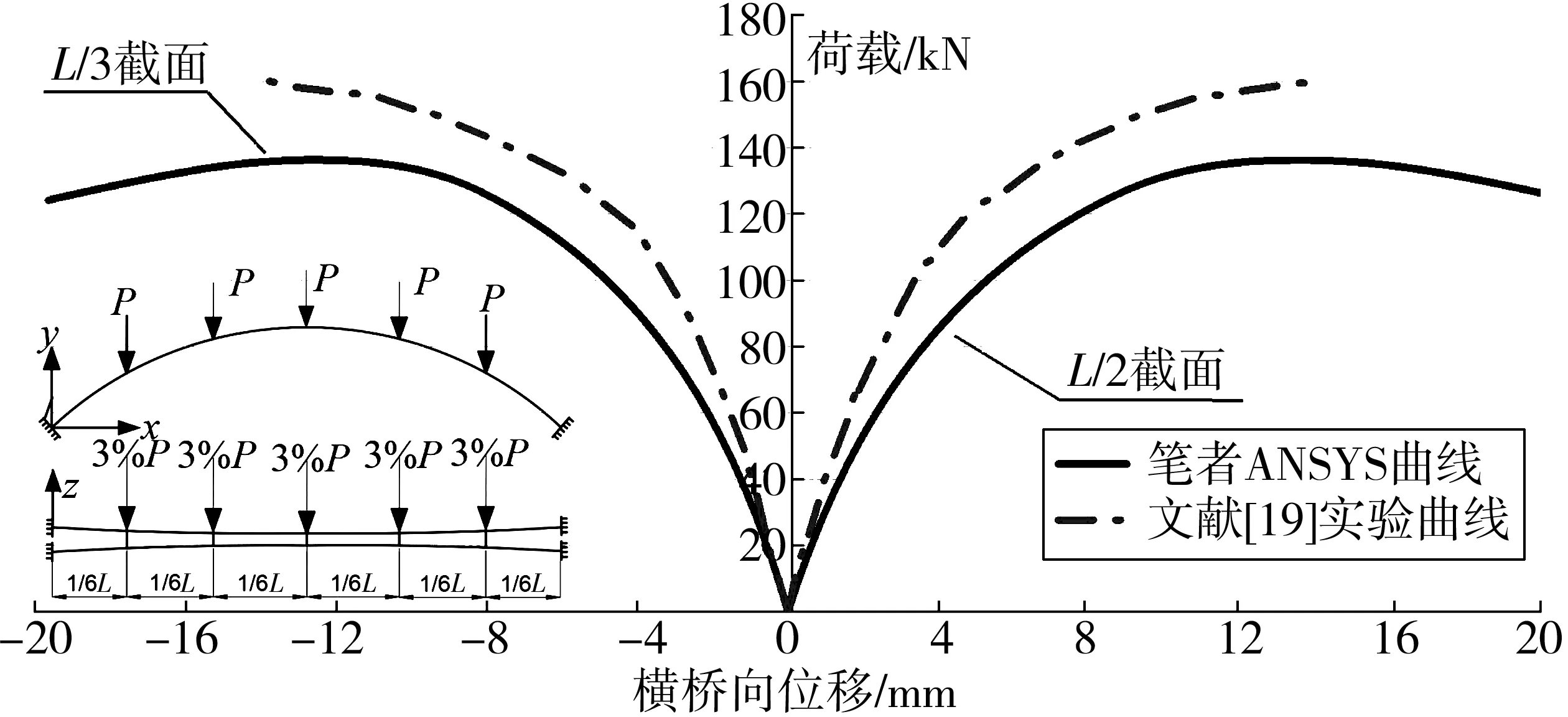
图4 双肋拱荷载-位移曲线Fig. 4 Load-displacement curve of double rib arch
2 劲性骨架拱桥施工非线性分析
2.1 工程背景及有限元模型
某上承式劲性骨架混凝土拱桥主桥长624 m,计算跨径600 m,矢高120 m,矢跨比1/5。桥面按两幅桥设置,单幅桥桥面总宽12.25 m。拱轴线采用拱轴系数m=1.6的悬链线,横向设置两片平行式箱形拱肋,拱脚截面12 m×6.5 m,拱顶截面8 m×6.5 m。两片拱肋横向中心距16.5 m,通过15片型钢混凝土的横撑连接成整体。拱上结构主梁为3联4×40 m预应力砼先简支后连续T梁,拱桥总体布置如图5。
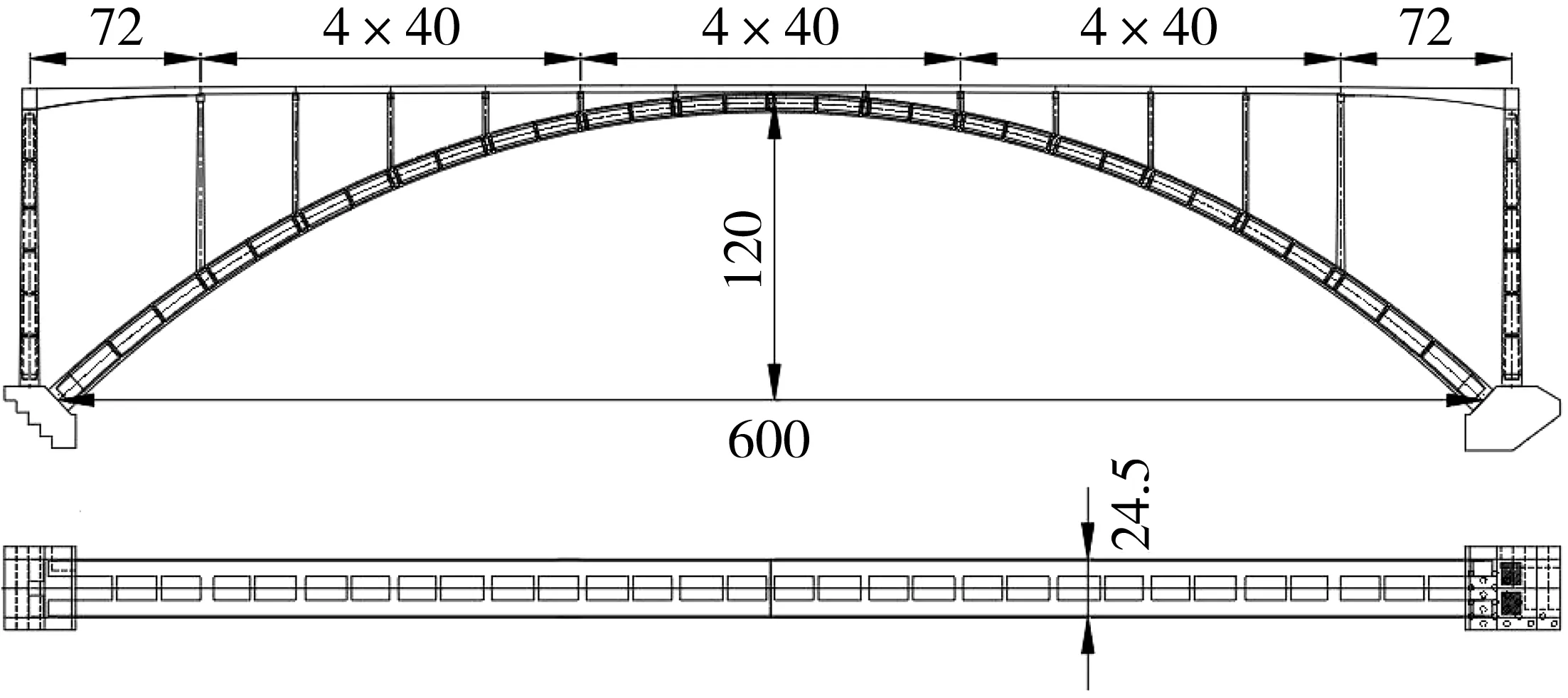
图5 某桥总体布置(单位:m)Fig. 5 Overall arrangement of a bridge
为分析劲性骨架拱桥拱圈在外包混凝土浇筑的各施工阶段的稳定承载力,使用ANSYS软件建立本桥主拱的有限元模型(图6),模型整体坐标系以纵桥向为X轴、竖桥向为Y轴、横桥向为Z轴。劲性骨架中的弦管、腹杆、平联、横撑均采用空间梁单元Beam188模拟,且拱肋上下弦管采用双单元法模拟。拱肋箱形外包混凝土和横撑混凝土采用壳单元Shell181模拟。约束拱脚及预埋段节点所有平动位移与转动变形以形成无较拱体系。钢管混凝土的灌注和外包混凝土的施工过程采用ANSYS的生死单元法。梁单元Beam188在构件连接点处进行离散划分单元,壳单元Shell181使用映射网格划分为边长0.5 m的四边形,整个模型划分为248 576个节点,232 648个单元。有限元模型中各部位的材料特性如表1。
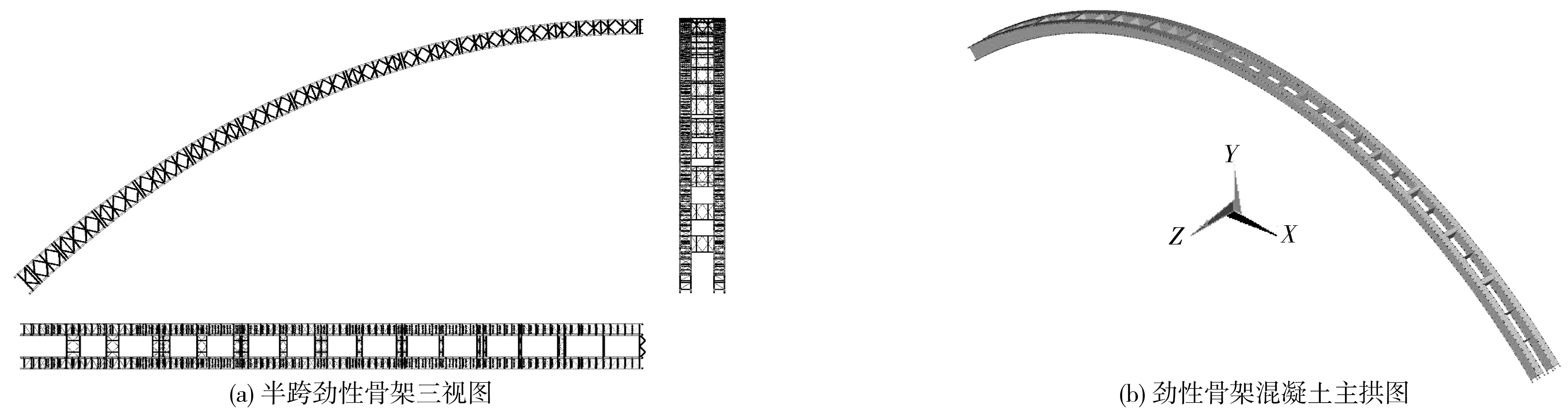
图6 主拱圈有限元模型Fig. 6 Finite element model of main arch ring

表1 有限元模型主要材料特性Table 1 Main material properties of the finite element model
根据1.2节所述的混凝土Hognestad模型和钢材四折线模型,笔者基于von Mises屈服准则及各向同性工作强化的假定,采用ANSYS多线性各向同性强化(MISO)选项模拟混凝土与钢材的本构模型如图7。
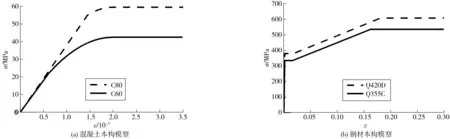
图7 材料本构模型Fig. 7 Constitutive models of materials
2.2 主拱圈屈曲分析工况
劲性骨架采用工厂内分段制作,现场预拼后用缆索吊装、斜拉扣挂悬臂拼装[20]。劲性骨架安装过程会经历一系列结构体系的转变:劲性骨架吊装过程中拱脚端铰接、另一端尚未合龙时结构处于悬臂状态,待骨架在拱顶位置永久合龙后即转变为二铰拱体系,最后浇筑封拱混凝土固定拱脚形成无较拱体系。待拱肋管内混凝土凝结完成后,利用安装好的劲性骨架作为拱圈浇筑外包混凝土支架,并采用纵向分8个工作面、竖向分为4环(表2)的“分环分段”方式对称同步浇筑外包混凝土。由于这种“分环分段”施工方法的特性,在每一环外包混凝土浇筑完成之前,混凝土板为数段分离的拱圈,此时混凝土板无法与拱圈协同受力,相当于仅以外荷载形式作用在劲性骨架上。这个荷载在每环混凝土合龙前的最后瞬间达到最大值,这个状态即为拱肋混凝土浇筑期间的最不利工况,笔者定义这个状态为“混凝土浇筑湿重阶段”。如底板混凝土合龙前一瞬间的状态为“底板浇筑湿重阶段”,该桥共有底板、下腹板、上腹板、顶板4个浇筑湿重阶段。由于顶板自重荷载与底板荷载大小相同,浇筑顶板时底板和腹板均已合龙参与劲性骨架受力,所以顶板湿重阶段的主拱稳定性必然会大于底板湿重阶段。为保证主拱混凝土外包阶段的稳定安全性,笔者将对底板、下腹板、上腹板这3个湿重阶段的结构稳定性进行研究分析。
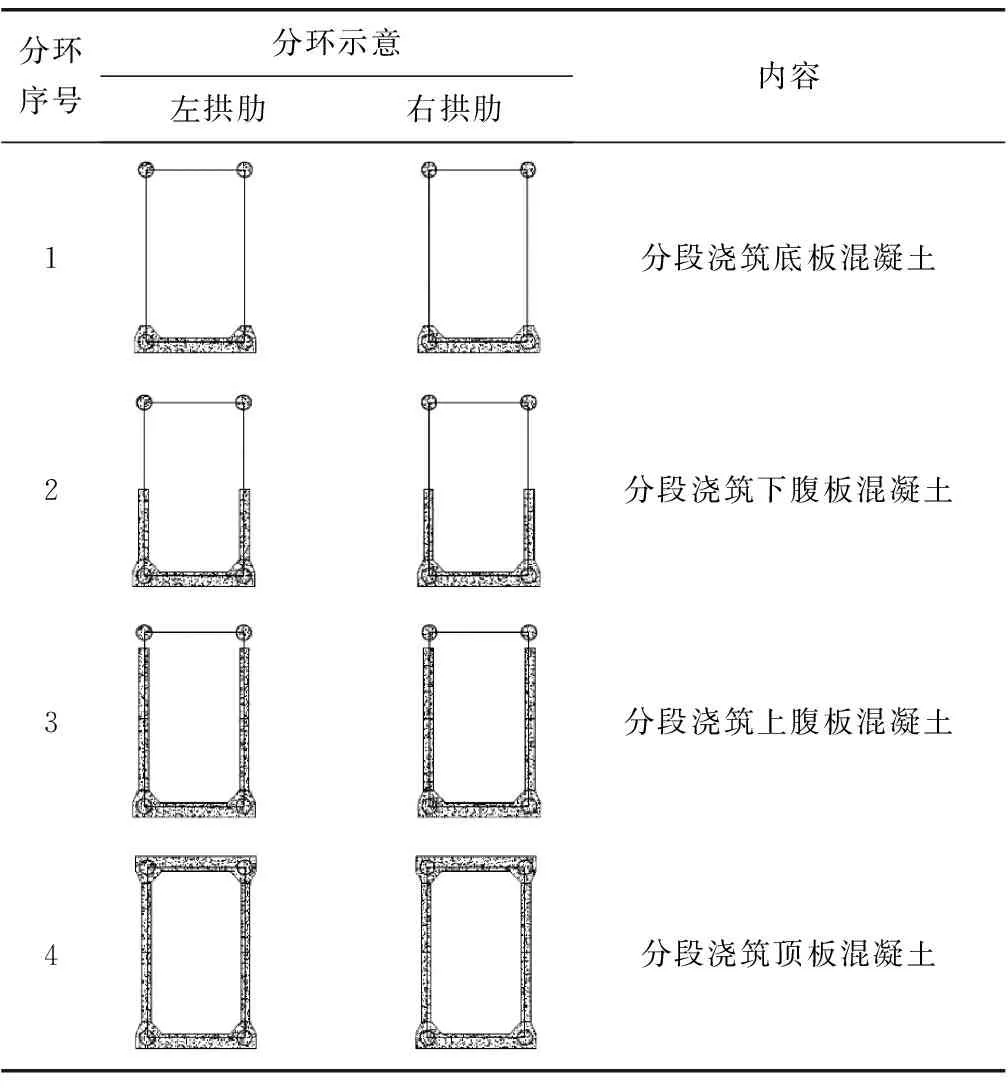
表2 拱圈混凝土分环浇筑示意Table 2 Diagram of concrete ring division pouring of arch ring
为模拟混凝土湿重,将处于湿重阶段下的外包混凝土的自重转换为节点荷载施加在劲性骨架上,以底板为例介绍湿重节点荷载大小的计算和分配方法:首先建立劲性骨架+底板混凝土的模型,只定义底板混凝土的材料密度并约束除底板节点外所有节点的所有自由度;随后对模型施加反向自重,对结构进行静力分析求解,得到的支反力即底板的湿重荷载。在结构非线性计算中以得到的湿重荷载作用代替混凝土底板的建模。通过上述方法得到各施工阶段的湿重荷载下结构初始荷载(Pbi+Pq)和外包混凝土自重下初始荷载如表3,每个施工阶段下的湿重荷载误差都不到0.2%,说明笔者方法能精确将混凝土自重转换为节点荷载。
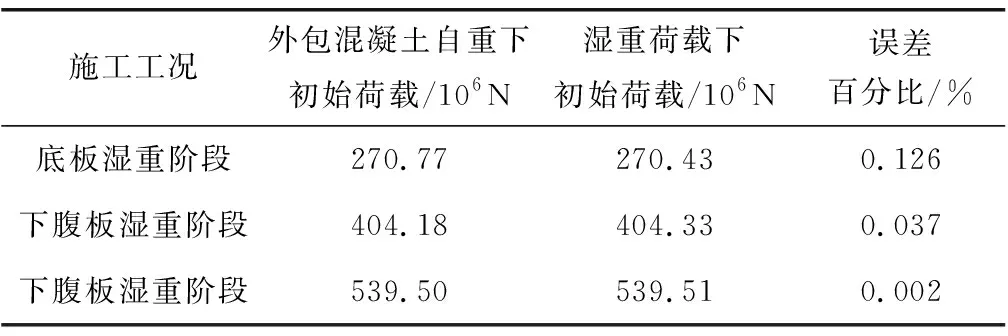
表3 各个湿重阶段的结构初始荷载Table 3 The initial load of the structure in each wet weight stage
2.3 主拱各湿重阶段非线性屈曲分析
劲性骨架混凝土拱桥在设计阶段由于预拱度设置不当、施工阶段由于施工误差、安装设备、工人熟练度、测量技术等原因会导致主拱线形在面内、面外均偏离原来的理想线形,使设计拱轴线形不可避免发生一定程度变化。在主拱施工阶段稳定性分析中,需计入几何初始缺陷的影响。几何初始缺陷通过将弹性屈曲一阶模态的位移乘以一个小的系数ξ施加在原模型上来实现。根据JTG/T D65—06—2015《公路钢管混凝土拱桥设计规范》中5.9.2规定,ξ可由式(4)计算:
(4)
式中:δ=L/5 000,为主拱允许的最大横向偏位值,cm;uzmax为主拱弹性一阶屈曲模态横向位移最大值,cm;L为主拱的净跨径,cm。
混凝土外包过程中,劲性骨架拱肋的一阶弹性屈曲模态均如图8,对一阶面外整体失稳形式,拱顶处横向偏位最大,因此可将一阶面外失稳模态中跨中横向位移设为12 cm,并按比例设置初始缺陷计算结构稳定系数。计入初始缺陷后,主拱在各个湿重阶段的不同非线性分析类型的荷载-位移曲线如图9。图9中的“加载系数”的含义与式(1)的“稳定性安全系数”相似,指的是非线性分析时,当前荷载子步下施加在结构上的荷载相对于“初始荷载”的倍数,稳定性安全系数见表4,括号中百分数指的是当前湿重阶段各分析类型下的稳定性安全系数相对于该阶段特征值分析的安全系数的百分比。

图8 主拱特征值分析一阶屈曲模态Fig. 8 First-order buckling mode of main arch eigenvalue analysis
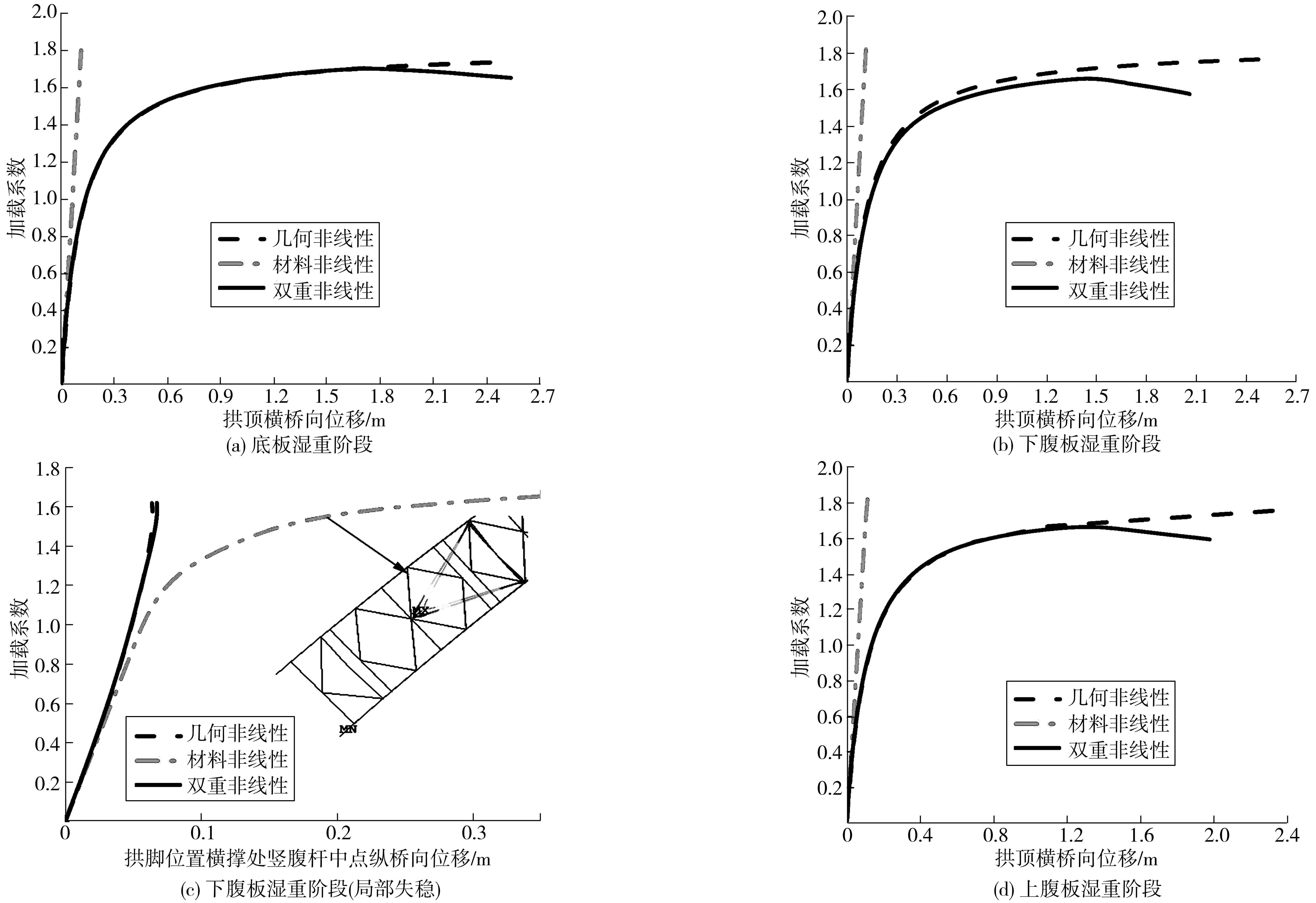
图9 各施工阶段非线性分析荷载-位移曲线Fig. 9 Load-displacement curves of nonlinear analysis of each construction stage
由表4可见,外包混凝土参与劲性骨架受力后会增强主拱的弹性稳定性,但随着外包混凝土的浇筑,主拱的变形和应力不断累积,双重非线性对主拱稳定性的降低越来越明显,从底板湿重阶段的6.6%增加到了下腹板湿重阶段的10.3%。
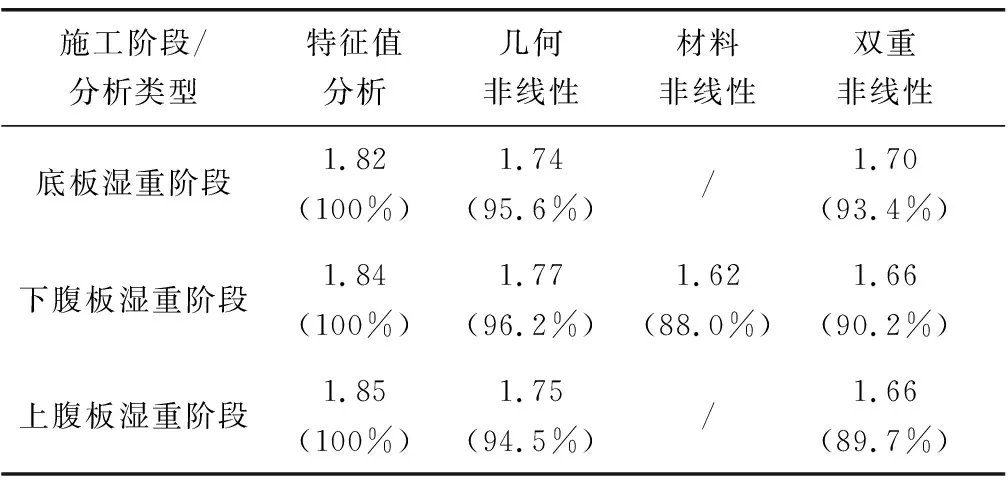
表4 各施工阶段在不同分析类型下的主拱稳定性安全系数Table 4 Main arch stability safety factors of each constructionstage under different analysis types
由图9可见,若仅考虑材料非线性,在结构加载的全过程中,荷载与拱顶横桥向位移始终为线性关系,结构没有发生整体失稳,说明劲性骨架主拱中的应力水平较低,构件都处于弹性工作状态。计入几何非线性影响后,劲性骨架因自身挠曲引起的在轴压力作用下的P-δ效应和拱顶侧向变形引起的在重力作用下的P-Δ效应,在结构中产生了附加弯矩,导致结构中的应力增长加快。随着荷载系数增加,核心混凝土和劲性骨架部分腹杆进入弹塑性或者塑性阶段,使主拱刚度下降,降低了主拱整体稳定性。在双重非线性分析中,由于材料非线性影响,底板、下腹板、上腹板湿重阶段的安全系数,比几何非线性分析的结果分别下降了2.2%、6.0%、4.8%,如表4。
分析不同施工阶段的荷载-位移曲线不难发现:不同的施工阶段下主拱的非线性表现形式不同。图9(a)中,双重非线性分析结果与几何非线性分析结果基本重合,这是因为底板湿重阶段外荷载相对较小、劲性骨架各构件应力较低,结构的非线性主要表现为几何非线性;在下腹板湿重阶段,由于混凝土浇筑在主拱内积累了应力,随着荷载系数的增加,部分材料进入塑性阶段,几何非线性和双重非线性的荷载-位移曲线开始分岔如图9(b),表现出了明显的双重非线性。上腹板湿重阶段由于底板和下腹板分摊了劲性骨架应力,在荷载系数较小时几何非线性和双重非线性结果重合,但由于该阶段初始状态荷载较大,结构在受力后期同样表现出了明显的双重非线性如图7(d)。
由图9(c)可见知:在下腹板湿重阶段的材料非线性分析中,发生了在拱脚位置横撑处的腹杆局部失稳现象。并且在几何、双重非线性分析中是无法发现的,说明结构的整体失稳可能会掩盖部分构件的局部失稳现象。因此,在劲性骨架拱桥的非线性屈曲分析中,有必要探讨不同类型的非线性分析下的结构失稳情况。实际施工中,在下腹板混凝土完全浇筑完成前,劲性骨架拱桥主要是以钢管混凝土弦管和型钢腹杆连接成的桁架拱结构。整体上来看,此时结构具有与带初始缺陷的实腹式截面拱相似的整体失稳特性,即在自重和混凝土荷载作用下可能发生平面外的极值点失稳;从局部上来看,拱肋截面上的内力(弯矩、轴力、剪力)均主要呈现为劲性骨架弦管及腹杆的轴力。劲性骨架拱桥的这种受力机理决定了其在实际施工中不仅会发生整体失稳,还可能发生弦管和腹杆的局部失稳,并由此导致整体失稳[21]。因此,虽然实际结构受力时同时存在材料和几何非线性,但双重非线性分析未发现的腹杆失稳现象,在实际施工中依旧是有可能发生。并且相对于其他全非线性分析类型,都未发现局部失稳的杆件,拱脚位置横撑处的腹杆无疑是劲性骨架拱桥设计中可能的薄弱点,笔者将在第3节分析腹杆局部失稳的原因并研究相应改进措施。
综上分析:就主拱整体稳定性而言,只单一考虑材料非线性或者几何非线性都会高估主拱的极限承载力,所以在评估劲性骨架拱桥整体稳定性时,必须同时考虑材料非线性和几何非线性的影响;就结构构件的局部稳定性而言,只进行双重非线性分析时可能不容易找到结构潜在的局部失稳的薄弱构造,为更清晰的认识主拱结构加载过程中的失稳机理,有必要仅分析材料非线性条件下结构受力行为的演化过程。
3 腹杆局部失稳原因及改进措施
3.1 腹杆局部失稳原因分析
拱箱下腹板混凝土浇筑过程的材料非线性分析中,发现靠近拱脚位置的横撑腹杆发生了失稳现象,如图10。具体表征为横撑腹杆发生显著的沿拱轴线方向的挠曲变形。针对横撑腹杆局部失稳的现象,笔者选取拱脚位置的横撑的局部拱圈探讨腹杆失稳的机理和原因。
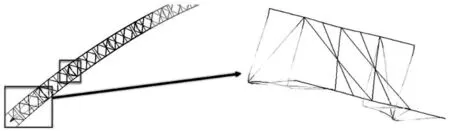
图10 劲性骨架局部失稳示意Fig. 10 Schematic diagram of local instability of stiff skeleton
浇筑下半腹板后的拱脚横撑位置的拱圈局部示意如图11(a),图11(b)为局部拱圈立面图,x方向为腹杆ab径向,y方向为腹杆ab处拱肋拱轴线方向。由图11可见,在下腹板湿重阶段,Δacd部分下腹板自重仅以荷载形式作用在横撑腹杆的下半部分ac,下腹板自重荷载G对腹杆的作用力可分解为沿x方向的Fx和沿y方向的力Fy。Fx使腹杆发生轴向伸缩,Fy使腹杆发生沿拱轴线方向的挠曲变形。腹杆ab在Fy造成的弯矩作用的平面外有斜撑ce、cg、ef这样的侧向支承如图11(c),因此不会发生弯扭失稳。腹杆ab可看作两端固结在钢管混凝土弦管上的超静定结构,因此腹杆ab中点c发生沿y方向的位移后会在腹杆内产生弯矩,并且由于腹杆ab在y方向没有设置其余支承,腹杆的挠曲变形仅由腹杆ab和斜撑ce、cg的抗弯刚度来抵抗,在Fy的作用下腹杆中点发生了较大的y向位移,从而腹杆中点和两端点处积聚了巨大的弯矩Mz,导致横撑内产生了巨大的应力。
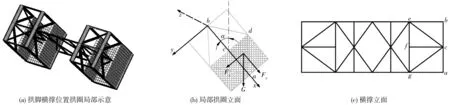
图11 拱脚横撑及局部拱圈示意Fig. 11 Schematic diagram of skew back transverse brace and local arch ring
为探讨横撑腹杆材料非线性失稳机理,笔者追踪了腹杆截面应力随加载系数的发展情况。如图12,当加载系数较小时,腹杆中点挠度、应力和荷载呈线性关系。随着荷载增大,腹杆中点部分截面边缘首先屈服(图13),截面刚度下降,腹杆开始发生塑性变形,腹杆中点应力不再增加,荷载继续增加导致腹杆截面屈服面积不断扩张,腹杆中点的挠度也开始表现为非线性的增长。此时,随着荷载的增大,挠度比线性阶段增长更快,导致了腹杆弯矩Mz的迅速增加,加速了截面的塑性发展。当加载系数达到1.59后,腹杆端点与中点附近区域已大面积屈服,构件抵抗能力大幅下降,此时荷载即使增加很少,腹杆也会发生很大的变形,最终导致腹杆失稳破坏。
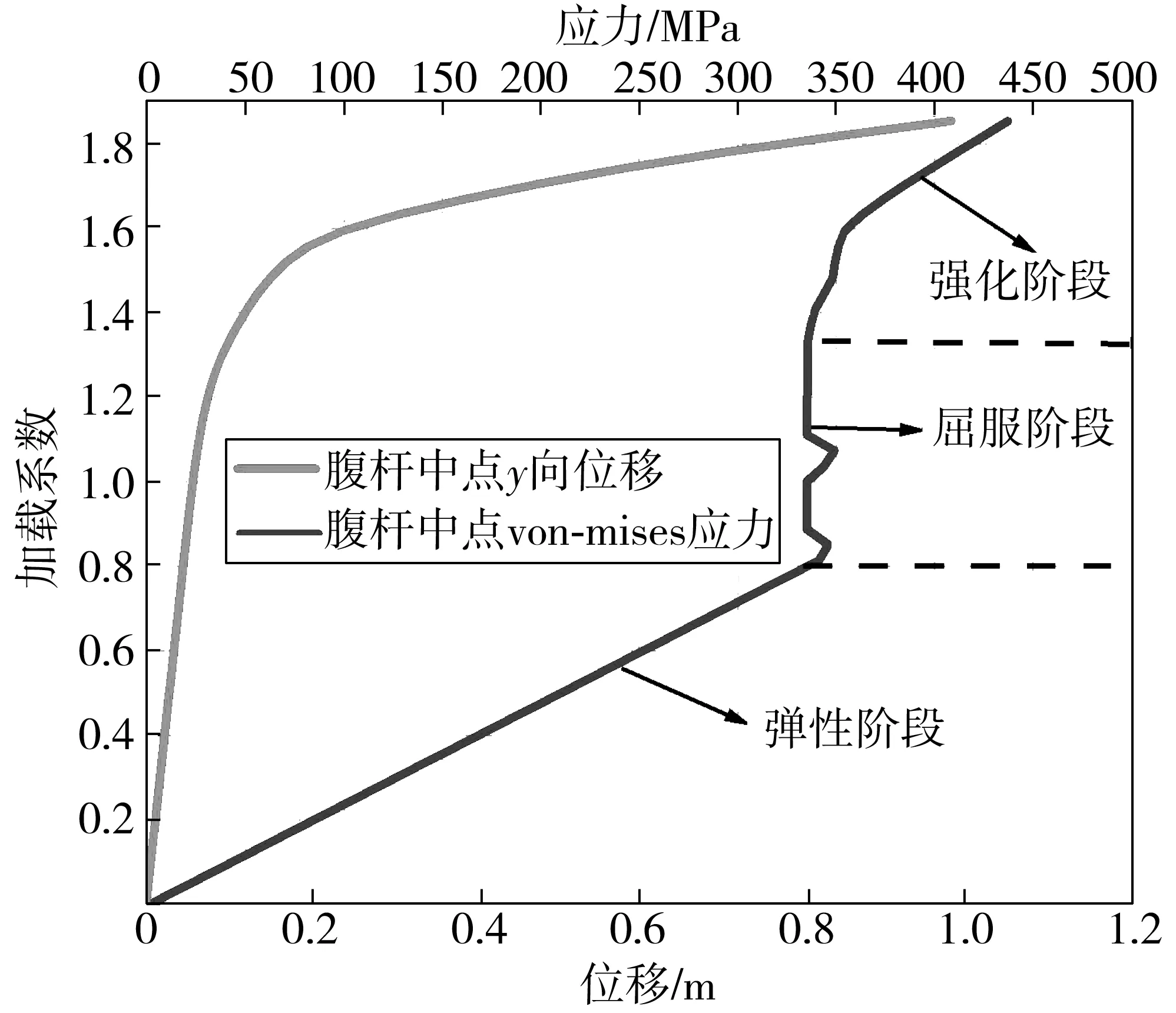
图12 腹杆ab中点荷载-位移、应力Fig. 12 Load-displacement and stress diagram at the midpoint ofweb member ab
综上分析可得,下腹板湿重阶段的材料非线性分析中,横撑腹杆失稳原因是,在下腹板湿重作用下腹杆发生了较大的挠曲变形。通过腹杆失稳的机理分析也解释了,为何只有靠近拱脚位置的横撑发生了失稳现象。对其余未失稳的横撑腹杆,由于从拱脚到拱顶的方向,横撑腹杆与竖向的夹角α越来越小,下腹板湿重对横撑腹杆的y向分力也随之减小。对那些α较小位置处的横撑腹杆由于受到的下腹板y向分量较小,在拱脚位置横撑失稳时这些横撑的腹杆材料尚未达到屈服强度,所以不会发生弯曲失稳。
3.2 横撑腹杆局部失稳的改进措施
通过上述分析,下腹板湿重的作用使腹杆发生了较大挠曲变形而导致了腹杆的弯曲失稳,所以保证腹杆的局部稳定性的关键是限制横撑腹杆的y向挠曲变形,对此,笔者将从结构设计和施工调整2个方面改善横撑腹杆的局部稳定性:
1)结构设计。采用与横撑相同的材料和截面形式,在横撑腹杆的y向布置斜撑来增强腹杆抵抗y向变形的能力,如图14。
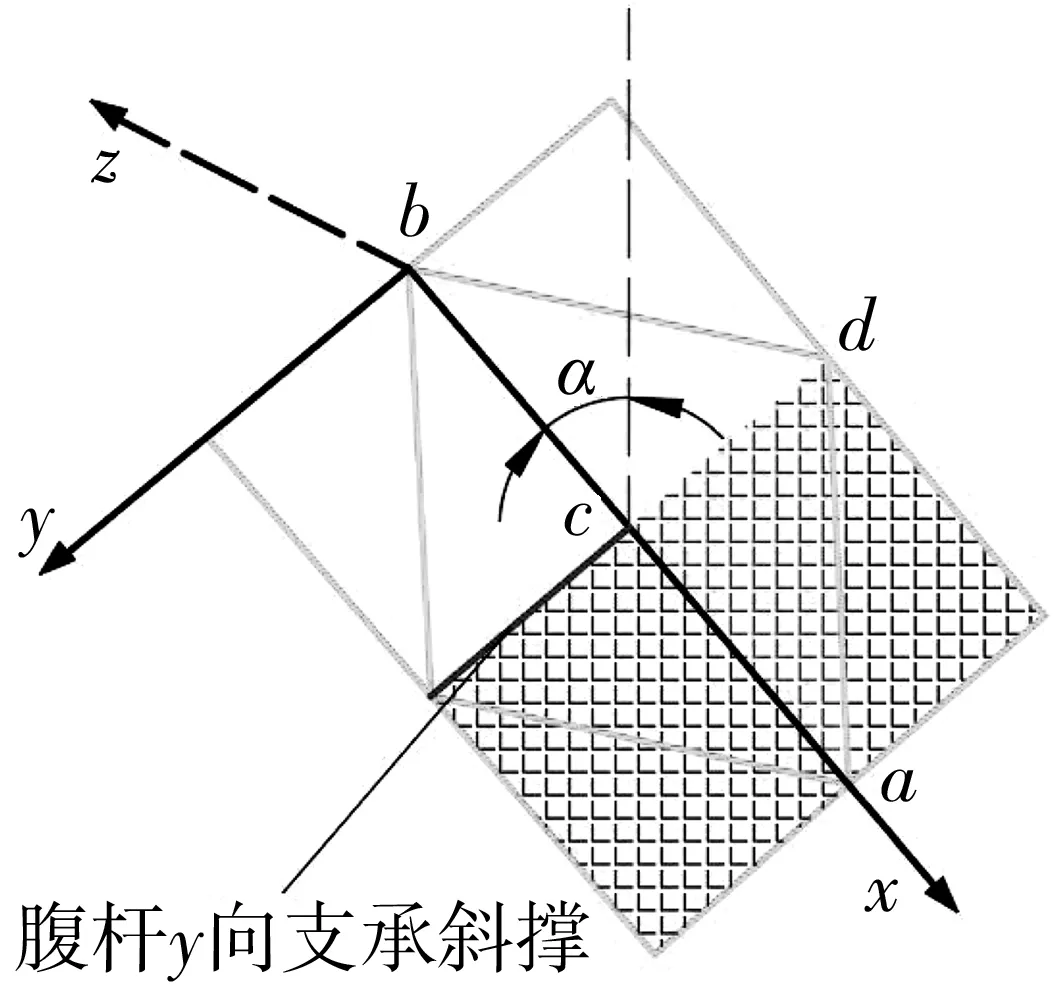
图14 腹杆y向支承示意Fig. 14 Schematic diagram of y-direction support forweb member
2)施工调整。在浇筑下板腹板混凝土前浇筑拱脚位置横撑混凝土如图15,使横撑混凝土协助腹杆共同抵抗下半腹板湿重作用。
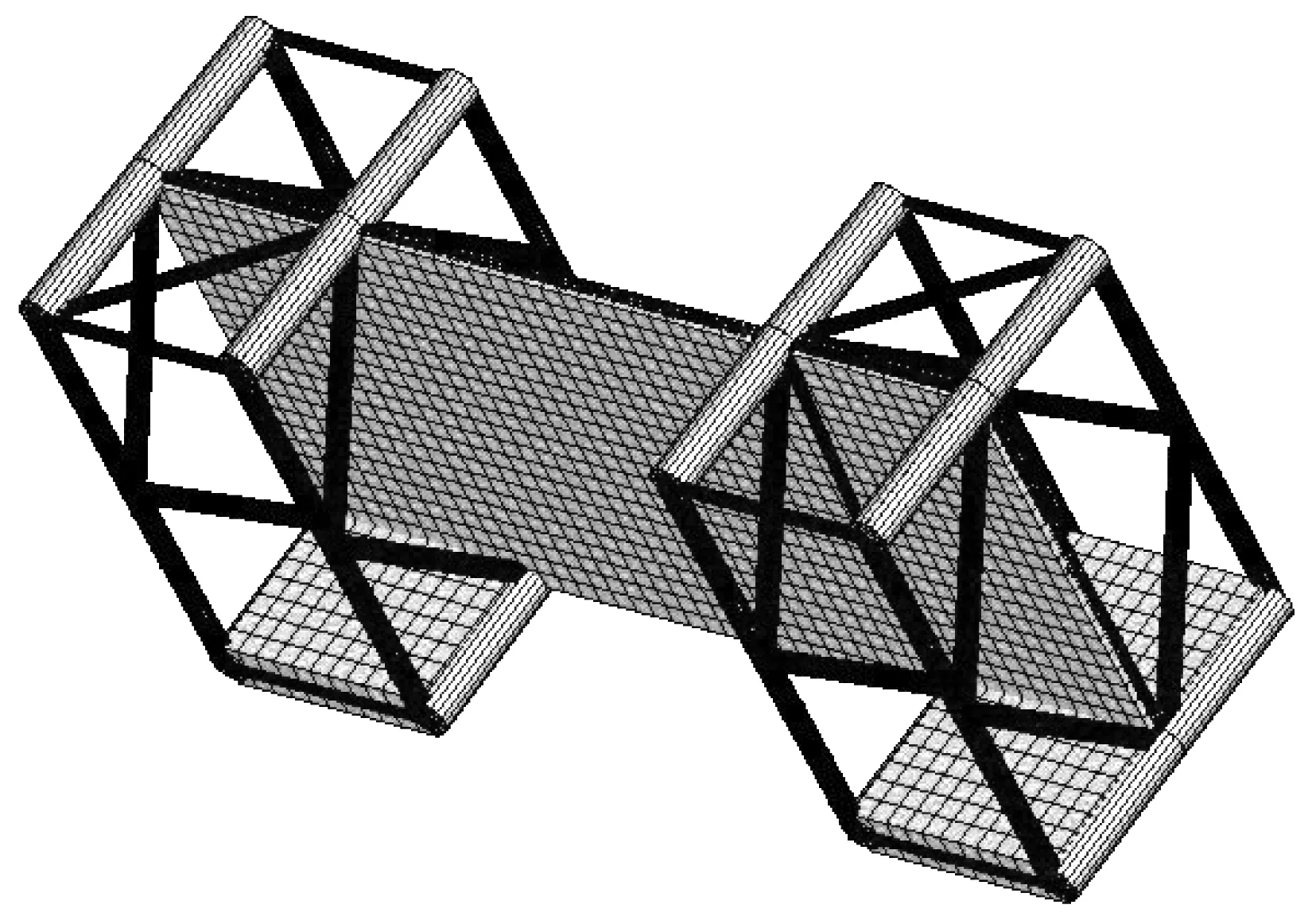
图15 横撑混凝土示意Fig. 15 Schematic diagram of transverse brace concrete
2种稳定性加强方案相同工况(下半腹板湿重阶段)下考虑材料非线性的荷载-位移曲线如图16。由图16可知,在加载的整个过程,2种方案腹杆ab中点的y向位移都较小,且都呈线性增长,说明两种方案都有效限制了腹杆ab的y向变形,加强了横撑腹杆的稳定性。对于方案1,仅需在横撑腹杆位置增设一根构件就可保证腹杆的局部稳定性,在不清楚哪些位置的横撑局部稳定性需要加强的情况下,在所有横撑腹杆增设斜撑也是比较方便、经济的方法;对于方案2,优势体现在不需要任何多余构件,仅仅通过调整施工顺序就能达到提高腹杆稳定性的目的,但横撑混凝土浇筑时也会影响主拱的瞬时应力和线形,当腹杆稳定性加强与线形、应力控制冲突时不适用。
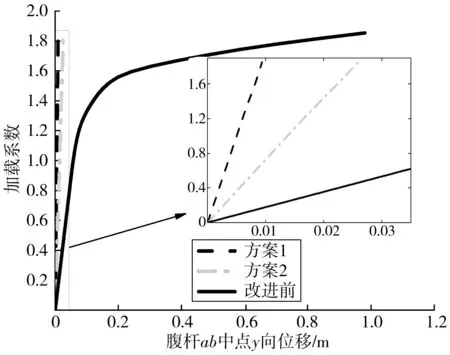
图16 不同方案下的荷载-位移Fig. 16 Load-displacement diagrams under different schemes
4 结 论
1)劲性骨架外包混凝土施工过程中,随着外包混凝土的浇筑,主拱的变形和应力不断累积,双重非线性对主拱稳定性的降低越来越明显,从底板浇筑阶段的6.6%增加到了下腹板浇筑阶段的10.3%。
2)研究发现劲性骨架拱在下腹板浇筑过程中靠近拱脚位置横撑腹杆出现了局部失稳现象,且横撑腹杆局部稳定系数比双重非线性分析中的整体稳定系数小2.4%,这表明部分构件的局部失稳是结构的整体失稳的前兆。
3)评估劲性骨架拱桥整体稳定性时必须同时考虑材料非线性和几何非线性的影响,否则会高估其稳定承载力;但只进行双重非线性分析时可能不容易找到结构潜在的局部失稳的薄弱构造,为了更为清晰的认识主拱结构加载过程中的失稳机理,有必要仅分析材料非线性条件下结构受力行为的演化过程。
4)拱肋间横撑腹杆失稳是在拱箱下腹板浇筑过程中混凝土湿重在横撑腹杆节间分量所诱发的,增加横撑腹杆支承斜撑或者在浇筑下腹板混凝土前浇筑横撑混凝土,可以有效加强横撑腹杆的稳定性。
