周期函数的原函数问题剖析*

蔡水英 李德新

(福建农林大学计算机与信息学院,福建 福州 350002)

0 引言

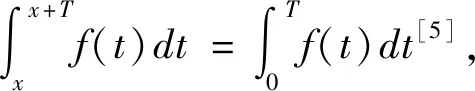
1 周期函数的原函数的分解

设函数f(x)的定义域为D，如果存在一个正数T，使得对于任一x∈D有(x±T)∈D，且f(t+T)=f(t)恒成立，那么称f(x)为周期函数，称T为f(x)的周期,通常我们说周期函数的周期是指最小正周期[2]。

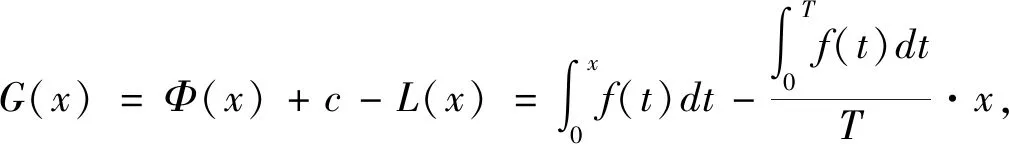
所以G(x)是周期为T的连续函数。从而有：

2 连续函数的原函数的周期性

引理1设f(x)是R上一个连续周期函数，则f(x)的所有原函数要么都是周期函数，要么都不是周期函数。

任取一个常数c，Φ(x)+c为f(x)的一个原函数。

若Φ(x)为周期函数，不妨设其周期为T(>0)，那么有：

Φ(x+T)+c-[Φ(x)+c]=Φ(x+T)-Φ(x)=0

因而根据周期函数的定义以及c的任意性可得，f(x)的所有原函数都是周期函数。

若Φ(x)不为周期函数，Φ(x)+c也不是周期函数。因而,由c的任意性可知，f(x)的所有原函数都不是周期函数，证毕。

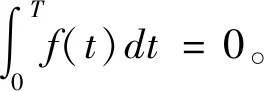
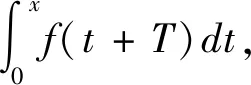
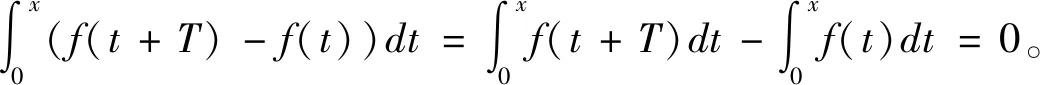
故f(t+T)-f(t)的所有原函数都是常数，所以f(t+T)-f(t)=0，即f(x)是周期为T的函数,证毕。

推论1:f(x)是周期为T(>0)的奇函数的充分必要条件是f(x)的所有原函数是周期为T(>0)的偶函数。

3 应用

由定理1可得以下推论：

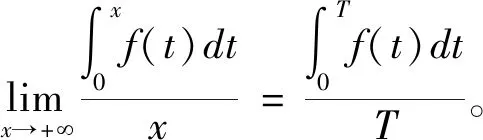
由于连续周期函数G(x)有界，所以可得：

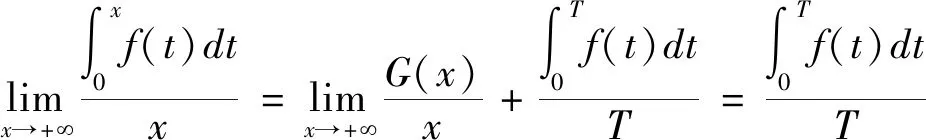
推论2说明了:当x→+∞时,f(x)在[0,x]上的平均值的极限为f(x)在[0,T]上的平均值。

由于

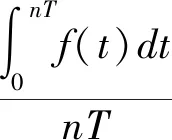
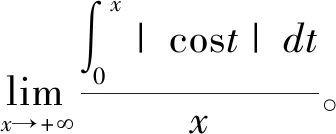
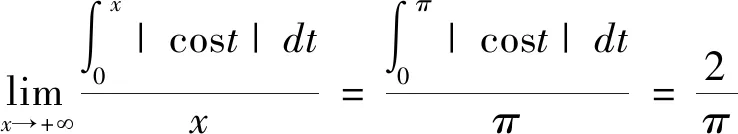
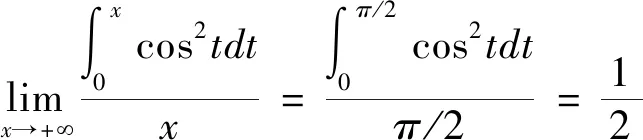
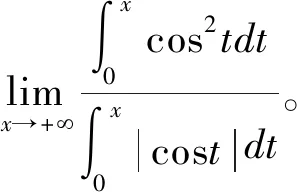
解:[法一]由推论2可得：

[法二]由推论3可得：

当x→+∞时，含有周期函数的变限积分的商式求极限问题，一般不能用洛必达法则，常见用夹逼准则求解，利用本文方法不失为一种简捷高效的途径。

4 结论