基于停留点密度聚类的轨迹区域划分方法
2021-11-09张厚禄唐云祁王子扬
张厚禄, 唐云祁, 王子扬
(中国人民公安大学侦查学院, 北京 100038)
0 引言
当今世界移动互联网技术蓬勃发展,人们的工作与生活被各类移动终端全面交叉覆盖。如何利用移动终端的行为数据分析行为人特点是数据挖掘的热门方向。轨迹数据区域划分是移动终端行为数据分析的重要研究分支,也常被广泛应用于公共安全防范及案件侦查。在公安机关实际工作中,通过分析目标人活动轨迹中包含的目的性信息,可以寻找犯罪嫌疑人并评估其可疑程度,以达到案前预警、案后侦查追踪的目的。现有的各种轨迹挖掘算法已经可以做到最大程度涵盖轨迹包含的所有信息,但是对于这些信息的应用程度有限。如连续针对某类地点(加油站、收费站、小区)实施犯罪或预备犯罪的场景,在没有任何既定证据或者线索的情况下,可通过对行人的轨迹信息进行目的性分析,进而检测其异常特性,这对于已发案件的侦查或者未发案事件预防都有重要的意义。而面对这一场景,现有算法受制于对轨迹区域划分的精度不足,难以从行为人的轨迹信息中挖掘出有用线索。
一般地,行为人的活动轨迹被表示为一条连续的曲线,这种表示方式较为直观,但并不直接体现行人的“目的性”。为阐释行人的日常活动中的目的性,各种研究都要首先区分出不同的轨迹区域。常见的思路是首先将速度不超过一定阈值的轨迹点迹定义为停留点,然后对停留点数据聚类以达到轨迹区域划分的目的。该方法首先从行人轨迹数据中检测得到停留点,然后将整个行人轨迹线抽象为若干连续停留点子集,这样行人的轨迹数据就被抽象为从一块停留区域至下一块停留区域的移动过程。如常见的下班回家,既是一个停留点(工作地点)到另一个停留点(家),也是一个目的地到另一个目的地。轨迹中的停留点,尤其是连续停留的点才包含行人的绝大部分活动信息。本文舍弃连续停留点之外的轨迹点,在连续停留点之间挖掘信息,利用停留点所隐含的信息来划分不同的轨迹区域。
1 相关工作
针对轨迹区域划分,许多学者都进行了广泛而深入的研究,从方法思路看,目前主流的方法是使用聚类将同一区域的轨迹聚集为一类,通过不同分类区分轨迹区域的方法。目前轨迹数据聚类策略主要有3个方向:基于结构或形状相似度的轨迹聚类方法、基于兴趣地点的聚类方法、基于历史活动周期的聚类方法。各方向采用的方法界限并不明显,且会互相交叉。
较早的研究中会使用一些常见的聚类算法如K-MEANS、STING[1]、DBSCAN[2]等,由于密度聚类方法可以发现任意簇的形状,近些年的研究重点都在改进DBSCAN算法上。为克服DBSCAN难以确定最佳参数的缺点,Chi[3]为提出HFDST算法,该方法将快速搜索方法应用于轨迹聚类,并通过两个参数Rho、Delta和递归函数来确定未分类的其他子轨迹,以达到克服DBSCAN算法参数敏感的问题;Xiaohui[4]提出一种抽样方法,使用DBSCAN识别分组以后根据持续时长和相似性评分,最后返回得分最高的K组;Peng[5]提出一种基于Spark和SPDBSCAN算法提升聚类效率的方法,该方法改进了DBSCAN算法使之能够并行进行,提升了计算效率;胡圆[6]提出一种基于RDBSCAN算法的异常轨迹检测方法,通过密度区分然后得到异常程度最高的TOP-N异常轨迹;江玉玲[7]采用Frechet距离作为相似度判别依据,改进了DBSCAN算法以对船舶轨迹进一步聚类;Feng[8]提出了基于密度的车辆轨迹聚集方法,该方法考虑到路网形状重建轨迹数据,通过密度聚类结果分析轨迹特性从而引导驾驶员避免交通堵塞;Chen[9]提出一种线性序列的提取方法,该方法首先分割轨迹数据,再计算相邻点的角度并使用DBSCAN方法对其进行聚类;袁志琴[10]提出一种面向变尺度密度数据的分级聚类算法,该方法提出的分步骤轨迹聚类思路较为新颖。
2 相关定义
为更好地描述后续工作的实现过程,当描述算法需要调用概念时,直接使用以下定义。定义图示如图1所示。
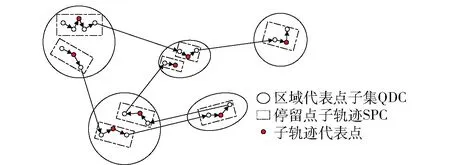
图1 相关定义图示
定义1 (轨迹,Trajectory Dataset)设TD(Trajectory Dataset)为一个轨迹数据集,点P为其中的轨迹点,则轨迹点按时间先后顺序可表示为TD={P1,P2,P3,…,Pn}。
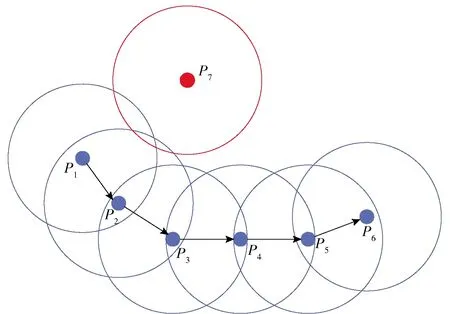
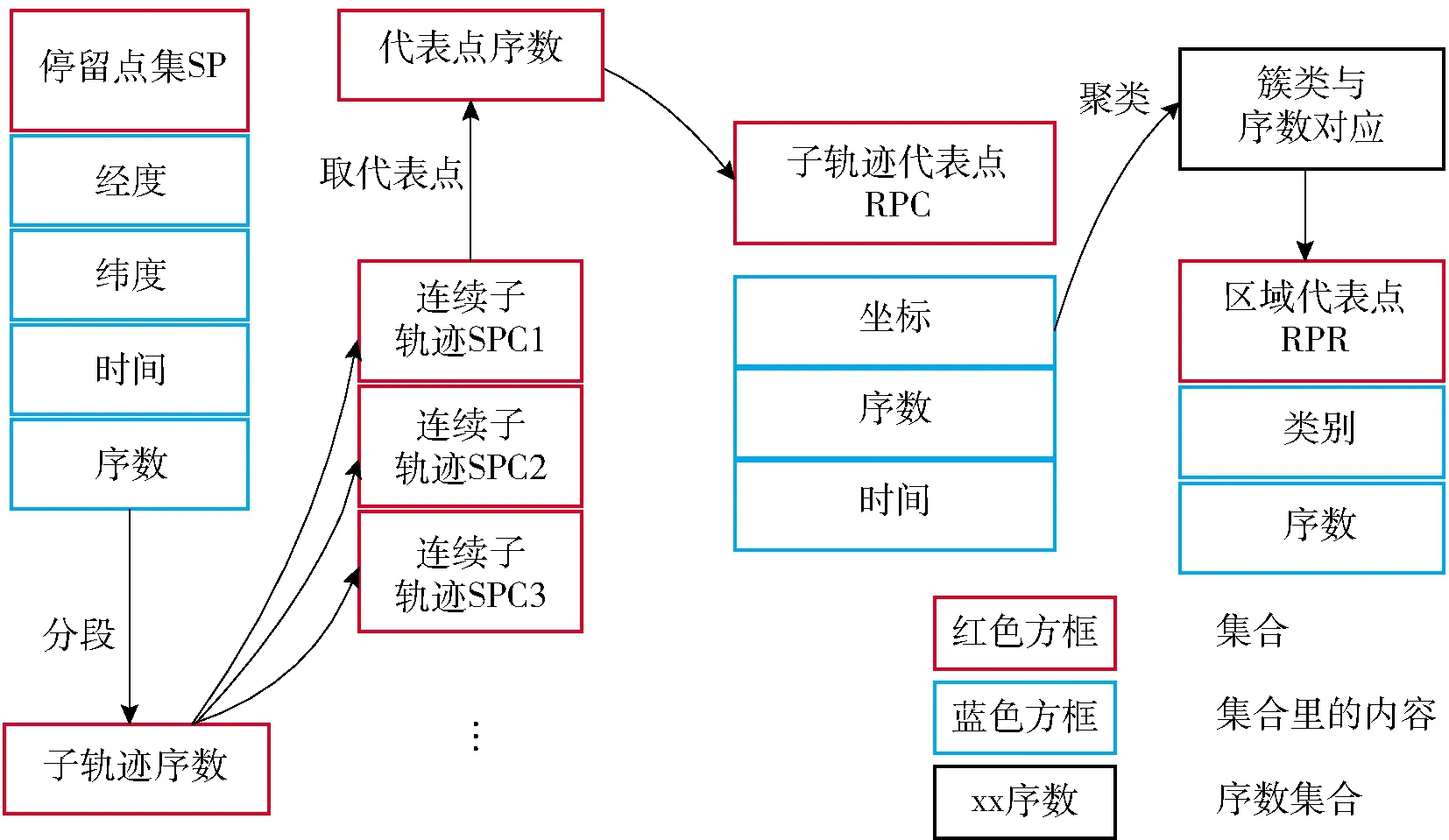
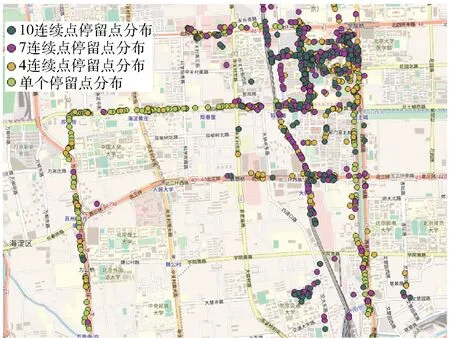
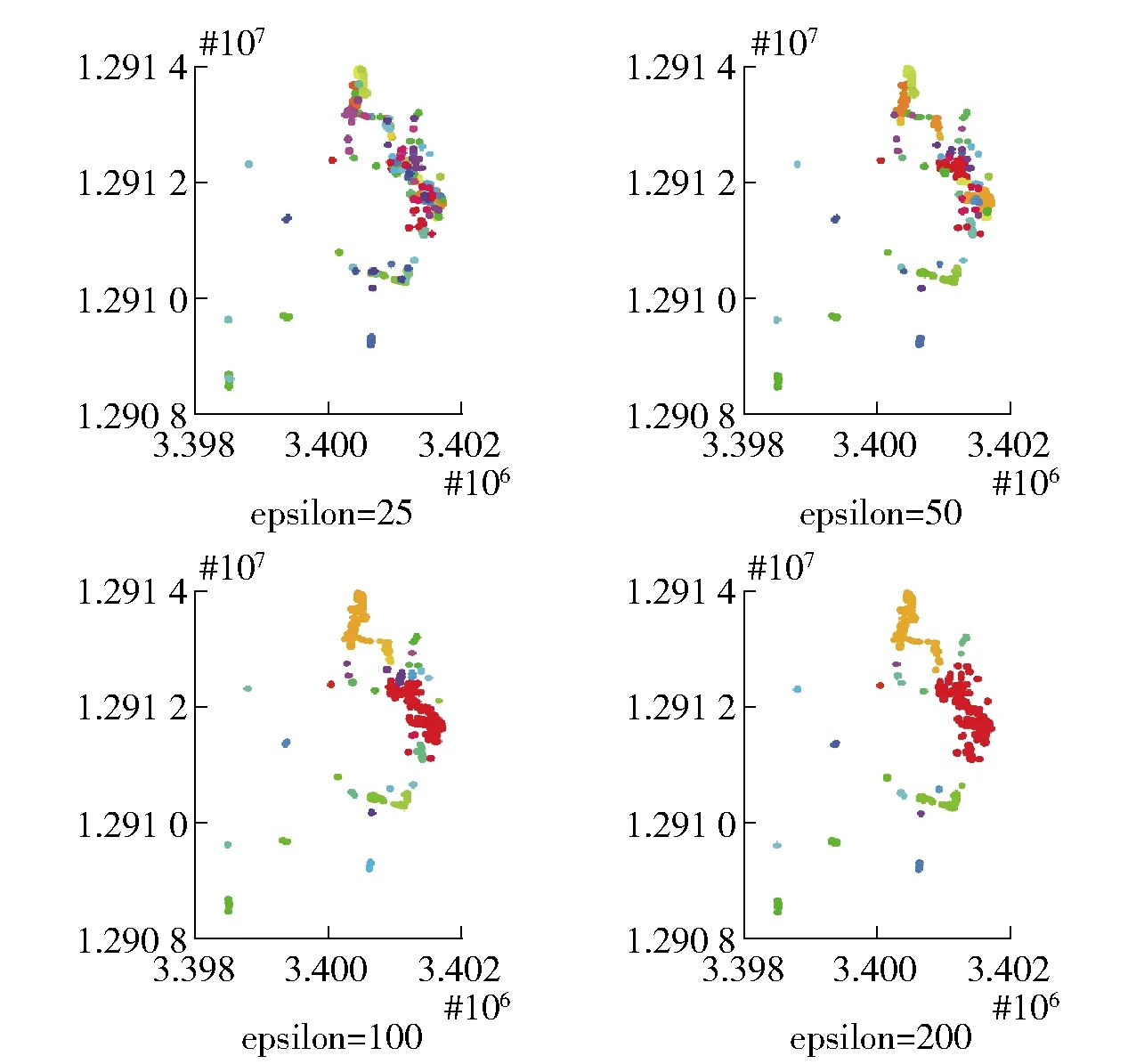
定义2 (停留点集,Stay-point Dataset)假设TD中停留点序数集合为TDON,TDON={a,b,c,d,…,i}((0 定义3 (子轨迹,Sub-trajectory Dataset)对于轨迹TD={P1,P2,P3Pn},假设存在整数1≤j 定义4 (连续停留点子轨迹,Sub-trajectory Dataset of Continually Stay-point)对于连续点序列数集合SP={a,b,c,d,…,i}(0 定义5 (连续停留点子轨迹代表点,Represent Point of Continually Stay-point Sub-trajectory)每个连续停留点子轨迹只保留一个点Q代表该子集的经纬度和时间,额外加上用户在该子轨迹中的总停留时间。对于连续停留点子集SPCm,其代表点Qm包含经度(Latm)、纬度(Lngm)、时间(Tm)以及子集内总停留时长(STm),全部的Q组成集合RPC。 定义6 (区域代表点,Response Point of Region)将子轨迹代表点按照密度聚类(Density Cluster)的方式聚集为QDC1、QDC2…QDCu等类。聚类完成后,每个类中取一个代表点形成区域代表点集RPR。 定义7 (行为模式,Behavior Pattern)经过密度聚类之后,子轨迹代表点按照时间顺序可组成一条新轨迹RTD,相邻两个不同区域代表点构成一组模式TPv(0 停留地点往往伴随着有目的性的用户活动。为突出目的性造成的轨迹异常,研究思路集中在用户在符合条件的停留点之间切换的频率。流程分3个大部分:停留点预处理(初步过滤数据)、密度聚类处理(地理空间上相近地点聚类)、模式匹配及异常筛选。具体流程如图2所示。 图2 流程图示 为直观查看点分布情况,首先将经纬度转化为地图中的实际距离。经纬度与现实距离转换关系如公式1: (1) 计算距离和速度时,两点Pi,pj之间距离计算[11]公式如公式2: (2) 将坐标转换为现实空间距离之后,就可以直接计算各个点之间的速度。速度计算出来之后,经过速度阈值V(一般取正常成年人平均步行速度1 m/s)过滤,形成停留点集SP以及连续停留点子集。此时的连续停留点子集中,包含有一些总停留时间很短的点,这类点多出现在路口附近,并不带有“目的”。为避免这些点造成干扰,只保留连续停留时长不小于1 min的连续子集。由于处理过后,同一轨迹相邻的停留点之间间隔都是10 s,所以连续停留点数目阈值设置为6。这样每个连续点集合就能至少代表一项活动[12],求得所有连续子轨迹的子轨迹代表点,组成代表点集NSP。具体算法实现如下。 算法1:预处理算法 Input:轨迹TD={P1,P2,P3,…,Pn},速度阈值V,停留点连续点数阈值num。 Output:连续停留点代表点集合NSP 1TJi→NSP 2 fori=1 tom-1; 3k=0;l=0; 5 if speedi 6k=k+1; 7INDk=i; 8 addPi&INDktoSP; 9 else 10 end if 11 end for 12 forj=1 tok 13 ifINDk+1=IND(k+1); 14 addSPjtoSPCl; ∥将连续的停留点归到一个子集 15 else 16l=l+1; 17 end if 18 end for 19 fori=1 tol 20 if numel (SPCi) 21 delet SPCi; 22 else 23 addSPCito NSP; 24 end if 25 end for 26 return NSP DBSCAN是一种经典的基于密度的非监督空间聚类算法,它可以将具有足够密度的区域划分成簇,可以在具有噪声的轨迹数据中发现任意形状的簇类,并将发现的簇类定义为密度相连的点的最大合集。以此为代表的密度聚类算法不需要指定类的数量。使用DBSCAN算法聚类轨迹数据以利用隐含语义的研究有很多,相关的研究非常充分。 要了解DBSCAN算法原理,首先有5个关键概念[13]:邻域、核心对象(Core Points)、直接密度可达(Directly Density-reachable)、密度可达(Density-reachable)、密度相连(Density-connected)。 邻域指的是指定对象p半径epsilon内的区域。 核心对象是指如果指定对象p的邻域内样本点数大于等于参数MinPts,则对象p就是核心对象。 直接密度可达指的是,对于一个集合TD,如果p在核心对象q的邻域内,则p从q出发是直接密度可达的。 密度可达指的是,对于集合TD,如果存在一个对象链P1,P2,…,Pn,P1=q,Pn=p,对于Pi∈TD,1≤i≤n,Pi+1是从Pi出发直接密度可达,则对象P是从对象q关于epsilon和MinPts密度可达的。 密度相连指的是如果存在对象O∈TD,使得对象P和q都是从o出发关于epsilon和MinPts密度可达,那么对象p到q是关于epsilon和MinPts是密度相连的。 如图3所示,各个点周围的圆圈代表了对象的邻域,P1对于P2来说是直接密度可达的,P1、P2、P3、P4、P5、P6之间彼此密度可达且密度相连,P7对于其余点则无联系。 图3 密度聚类示意图 考虑到在现实中,个人活动频繁的地点呈现出一种地点与目的性混杂的分布情况,表现为其活动点不是点状或线状分布的,而是呈现出区域化、多目的性混杂的状态。DBSCAN (Density-Based Spatial Clustering of Applications with Noise)聚类方法[14]可以适应多种聚类形状,可以将不同活动区域聚类成不同类别。 在DBSCAN概念的基础上,聚类完整过程如下:首先在子轨迹中搜索出密度极大点,将极大点定义为子轨迹代表点,每个子轨迹的代表点组成子轨迹代表点集,在子轨迹代表点集中搜索密度相连的点聚集成簇,同时输出簇中密度极大点,输出为区域代表点。区域代表点代表了某个区域内的所有停留点,因此可以看成是一类活动。 DBSCAN算法有两个参数,分别是epsilon和minPts,其中epsilon控制簇生长过程中的搜索半径,minPts控制最小簇点的数量。将DBSCAN算法的生长器部分做出了调整:生长器在搜索同簇类时,不产生噪声簇,取而代之的是产生零散的小簇,并且所有点都被归入簇中。这样就可以使用密度聚类的簇标号代表点的位置,后续算法就不必关注具体的坐标数据。这给后续异常检测算法减小了复杂度,并且也保证了数据的可靠性。具体过程如算法2所示。 算法2:密度聚类及模式输出算法 Input:NSP,epsilon,minPts Output:RTDBP 1.c=0; 2. IDX=DBSCAN(NSP,epsilon,minPts) 3. fori=1 to max(IDX) 4. a=find(IDX==i); 5. QDCi=NSP(a); ∥轨迹数据编码化 6. end for 7. fori=1:numel(NSP) 8. ifIDXi+1=IDX(i+1) 9. nexti 10. else 11.c=c+1; 12.TPc=(IDXi,IDX(i+1)); 13. end if 14. end for 15. returnRTDBP; ∥输出行为模式集合 在处理过程中,轨迹数据输出的内容也发生了较大的变化。为了保证代表点集合能够逆推到最初停留点集SP中的经纬度等原始信息,在算法运算过程中一直使用序数保留了各点集之间关键数据的映射信息,以减小算法运行时的复杂度。序列的映射作用如图4所示。 图4 轨迹点集中的序数起到的映射作用 实验环境为Windows10、64位系统,Intel Core i7-9750H@2.60 GHz CPU,16 GB内存,512 GB+1 TB固态硬盘,软件为MATLAB R2016a,QGIS 3.12.2。实验数据集Geolife数据集[15]是微软研究Geolife项目从2007年4月到2012年8月收集的182个用户的轨迹数据。这些数据包含了一系列按时间先后产生的点,每一个点包含经纬度、海拔等信息,共17 621条轨迹。 为展示实验过程,选用005用户(包含109 046个轨迹点)作为例子。实际生活中,人的步行速度大约是1 m/s,用这个速度作为阈值V,将不超过此速度的点划入停留点集SPTD。实验中多数数据是以5 s为一个间隔采集的数据,所以可以通过观察连续停留点数量反映轨迹持续的时长和分布区域之间的关系。 为验证连续停留点数目取6是否符合直观印象中的“既能过滤掉零散的点,又不会损失包含活动信息的数据”,文中遍历了num取1~10的所有情况,取其中1、4、7、10为例子,在GIS平台上效果如图5所示。 图5 005用户不同连续数量停留点的分布图示(部分) 从图5中可以发现,连续停留点子轨迹的连续数量越大、分布范围越集中、长时间活动的点更多;连续停留点的连续数量越小,分布越分散、长时间活动的点更少。经观察,当连续停留点数量大于6(总停留时间大于60 s)时,停留点在路网中分布明显少很多,分布相对集中,此时既可以排除意外情况造成的停留点干扰,也可以减少后续密度聚类算法的复杂程度,方便与其他算法对比效果。 为控制预处理部分中两个经验值(停留点速度阈值V和连续停留点数目num)可能对实验结果和对比算法产生的影响,后续实验不论是本文算法还是用作对比算法,都使用预处理后的数据实验对比,以保证对比实验所用数据集完全相同。 筛选完符合条件的连续停留点子轨迹后,计算出子轨迹代表点。对所有子轨迹代表点的经纬度密度聚类,聚类结果代表了地理空间中距离相近的停留点。密度聚类的参数只有epsilon(minPts是判断噪声点的值,必须取1,以防止噪声点集破坏点的分布)。为大致确定epsilon的最有取值范围,分别取25、50、100、150、200进行实验聚类。实验结果如图6所示,图中不同颜色代表不同的聚类簇。 图6 不同epsilon取值对聚类的影响(部分) 不难发现,epsilon取较小值时,聚类较为精细,划分出的轨迹区域也更为精细。分别以15、20、25代入。为提高区分的细粒度,模式频率阈值S不宜太大,因此分别取4、5、6。 按照划分区域是否正确,不同参数下算法划分区域的精确率(Precision)正确率(Accuracy)如表1所示。 表1 本文算法不同参数情况下区域划分的精确率和正确率 % 为验证方法的准确性,在相同环境、同样经过预处理的数据集条件下,与OPTICS算法取较优解时的结果做了横向对比。OPTICS算法是DBSCAN算法的改进版本,可以遍历DBSCAN各项参数下的聚类结果,以辅助确定DBSCAN最优参数。其参数有minPts和epsilon,但这两项参数只是一个形式,并不会影响到相对输出顺序,也不会影响最优结果。 当minPts分别取3、5、7,epsilon取15时,实验结果如表2所示。 表2 OPTICS算法不同参数情况下区域划分的指标 同样的数据从开始处理到算法运行结束,OPTICS算法运算时长为0.5 s。文中提出方法运算时长为0.1 s,使用时间略短。除去预处理部分,文中方法将轨迹数据多次精简,密度聚类的数据量很少,因此复杂度也很小。该方法的空间复杂度S(n)=O(f(n)),时间复杂度最大为T(n)max=O(3n),而OPTICS算法的时间复杂度为O(n2)。 通过实验结果得到的准确率和正确率,以及与OPTICS算法比较的结果,可以得出以下结论。 (1)算法能够较好地识别出轨迹区域,参数选取最优时,其正确率可达76%,同时精度也很高。 (2)与OPTICS算法结果对比可得,OPTICS算法对于精细化区域划分效果很差,精确率只有22%左右。而文中算法得到的结果精确率稳定在90%左右,计算精度比OPTICS约高70%。 (3)提出的方法对参数输入比较敏感。epsilon取15和取25,正确率差别较大(7%),实际应用时要注意参数选择。3 算法流程
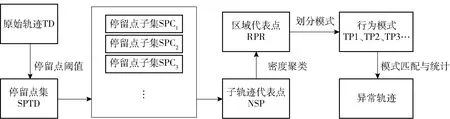
3.1 预处理
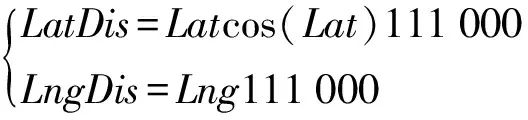
3.2 密度聚类
4 实验结果
4.1 实验数据预处理
4.2 实验数据预处理

4.3 与其他方法对比

5 结论
