基于状态估计的无人车前轮转角与横摆稳定协调控制
2021-11-09陈特徐兴蔡英凤陈龙孙晓强
陈特, 徐兴, 蔡英凤, 陈龙, 孙晓强
(1.江苏大学 汽车工程研究院,江苏,镇江 212013;2.江苏大学 汽车与交通工程学院,江苏,镇江 212013)
汽车工业的整体技术水平和整个产业链条已逐渐成熟和完善,并不断寻求新的突破. 智能车辆能够有效提高车辆的道路利用率和乘客舒适度,降低潜在的道路交通风险,车辆的自主控制能力也满足了当前消费者日益增长的驾驶和乘坐需求[1-3],从而使得智能车辆研究成为行业当前的重要发展方向之一. 得益于车辆电子控制技术的成熟和普及,以及日益完善的中下游零部件供应渠道,产业链的发展壮大为无人车辆智能控制技术提供了可靠保障[4-5].
随着传感技术的发展、高精度传感器的普及,以及车辆控制技术的不断进步,车辆自动驾驶技术研究和工业应用已逐渐实现[6-7]. 轨迹跟踪控制是自主车辆无人驾驶过程中常见的场景,在轨迹跟踪中,通过对车辆的转向运动控制,实时地减小轨迹跟踪偏差和航向偏差,以达到接近参考轨迹的目的. 为了解决不同情况下的轨迹跟踪问题,目前已有许多相关的研究成果[8-10]. 借助车辆上的各种传感器,自主车辆能够实时感知和识别车辆周围的驾驶环境和车辆本身的驾驶状态. 然后,无人车辆智能控制系统基于所有传感器信息对车辆运动控制做出正确的决策和规划,引导车辆执行器组进行统一协调运动,完成轨迹跟踪的目的,避免交通风险[11-12]. 目前,许多研究集中在无人车辆轨迹跟踪和稳定性协调控制上,其中模型预测控制算法得到了广泛的应用. LIN等[12]考虑并集成了轨迹跟踪控制、纵向控制、横向控制和直接横摆控制模型,提出了一种分层的车辆协调控制策略,结果表明,所提出的控制策略在满足智能车辆轨迹跟踪要求的同时,也能保证车辆自身稳定性.
自主车辆能更好地满足使用体验,避免驾驶员自身安全,并能避免因驾驶员非熟练驾驶或抢道等危险行为造成的交通流阻塞. 在多信息流的作用下,一个好的车辆控制器能够更好地考虑控制精度和车辆安全性. 因此,近年来,研究人员逐渐开始关注多因素耦合下的车辆轨迹跟踪控制问题,如未知扰动和模型参数不确定性对车辆控制器的影响,以及执行器子系统相互作用下的协调控制问题[13-15]. KAPANIA等[15]将轮胎摩擦极限条件作为无人车稳定控制器设计的关键因素,采用前馈控制和反馈控制结合的方式设计了无人车鲁棒控制器,提高了车辆的轨迹跟踪精度和转向不足特性.
文中设计了一种基于状态估计无人车前轮转角跟踪和横摆稳定协调控制策略. 考虑到实际车辆前轮转角难以通过传感器直接测量得到,设计了一种前轮转角估计方法,并将估计结果作为控制输入量. 利用滑模控制理论分别设计了前轮转角跟踪控制器和车辆横摆稳定控制器,用于跟踪参考前轮转角和参考横摆角速度,从而实现无人车轨迹跟踪和横摆稳定协调控制.
1 无人车辆系统建模
1.1 轨迹跟踪模型
如图1所示,不考虑空气阻力和悬架系统对车辆动力学特性的影响,只考虑车辆在水平面上的运动,建立了轨迹跟踪过程中的车辆模型. 图1中,oxy为车辆坐标系,其中x轴前进方向表示前进方向,y轴与x轴垂直指向为驾驶员从右至左,OXY为大地坐标系. 车辆沿x轴、y轴的动力学平衡方程可表示为
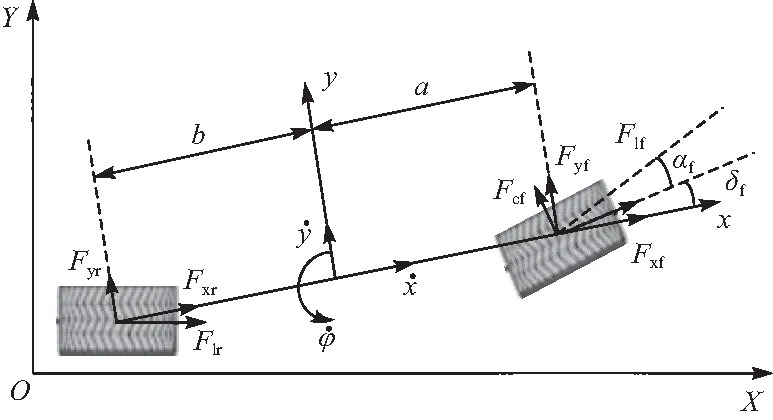
图1 车辆轨迹跟踪模型Fig.1 Vehicle trajectory tracking model
(1)
(2)
(3)
式中:m为汽车质量;a为车辆质心距前轴的距离;b为车辆质心距后轴的距离;Iz为绕z轴的转动惯量,φ为车辆的航向角;Fxf和Fxr分别为前、后轮胎沿着x轴的纵向轮胎力;Fyf和Fyr分别为前、后轮胎沿着y轴的横向轮胎力. 当前关于无人车辆轨迹跟踪控制研究中,无人车一般以中低速行驶,不会出现极端驾驶情况,因此可以认为轮胎力在线性区域内工作. 则轮胎力可表示为
Fxf=Clfsf,Fxr=Clrsr
(4)
Fyf=Ccfαf,Fyr=Ccrαr
(5)
式中:Clf和Clr分别为前、后轮胎的纵向轮胎刚度;sf和sr分别为前、后轮胎的轮胎滑移率;Ccf和Ccr分别为前、后轮胎的侧偏刚度;αf和αr分别为前、后轮胎的轮胎侧偏角. 轮胎侧偏角可表示为
(6)
式中,δf为前轮转角. 联立式(1)、(2)、(3)和式(4)、(5)、(6),可得用于轨迹跟踪控制的车辆动力学模型为
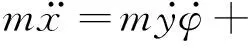
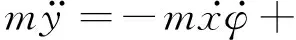
(7)
大地坐标系中的车辆坐标方程可表示为
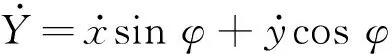

(8)
1.2 转向系统模型
齿轮齿条式车辆转向系统如图2所示. 当转向电机工作时,转向电机的输出扭矩首先传递给转向柱,转向柱上的动力学方程可表示为

图2 无人车辆转向系统模型Fig.2 Steering system model of unmanned vehicle
(9)
式中:Jsm为转向柱系统的转动惯量;θs为转向柱的转向角;Csm为转向柱系统阻尼;Ksm为转向柱系统刚度;Ts为转向电机驱动扭矩;τλ为转向梯形系统作用在齿轮上的反作用力矩. 转向电机带动转向柱转动,随着转向柱的运动,通过齿轮齿条带动转向横拉杆. 通过转向梯形系统,带动车辆前轮完成车辆转向运动. 则车辆梯形转向系统中从转向齿轮到车辆前轮转角的的动力学方程可表示为
(10)
式中:Jfm为转向梯形系统的转动惯量;Cfm为转向梯形系统的阻尼;Kfm为转向梯形系统的刚度;Mz为轮胎回正力矩;τs为转向管柱作用于齿轮齿轮的力矩. 根据式(9)和式(10),则转向系统的等效动力学方程可表示为
(11)
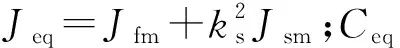
2 前轮转角跟踪与横摆稳定协调控制
2.1 协调控制策略
为了在实现车辆轨迹跟踪的同时确保车辆横摆稳定性,设计了基于状态估计的前轮转角跟踪与横摆稳定协调控制策略,如图3所示. 基于模型预测控制方法设计了车辆轨迹跟踪控制器,实时跟踪参考轨迹并计算得到所需的车辆前轮转角需求,即期望前轮转角. 将期望前轮转角输入到车辆转向控制模块并作为其控制目标,基于滑模控制方法设计了前轮转角跟踪控制器. 考虑到实际的前轮转角难以通过传感器直接测量得到,设计了一种新的前轮转角估计方法. 将前轮转角输入作为车辆模型的未知输入量,通过对车辆模型的解耦,分离出未知输入的解析式,并设计了未知输入观测器来实现前轮转角估计. 将前轮转角的控制需求和前轮转角估计值分别作为前轮转角跟踪控制器的参考值和实际值,计算得到转向电机的输出扭矩,从而满足车辆转向控制需求. 此外,为实现车辆横摆稳定控制,设计了滑模控制器跟踪参考横摆角速度.

图3 协调控制策略Fig.3 Coordinated control strategy
2.2 轨迹跟踪控制器设计
式(7)中的车辆轨迹跟踪模型是非线性的,为提高车辆控制的精度和实时性,对车辆模型进行线性化处理,得到如下的线性时变方程
(12)
(13)
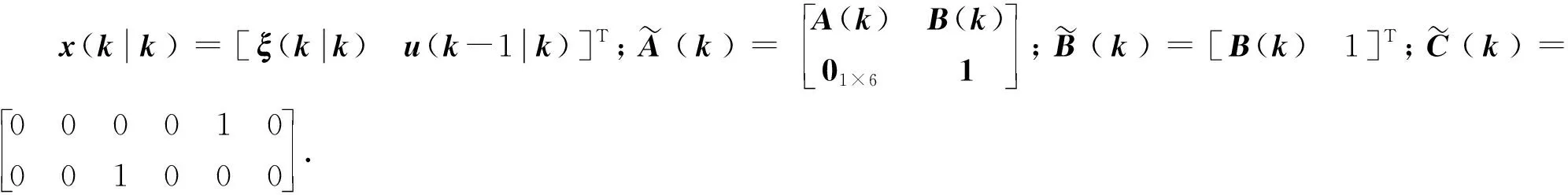
Y(k+1|k)=Ψξξ(k)+ΘξΔU(k)
(14)
式中,Y(k+1|k)为k时刻系统输出,ΔU(k)为k时刻系统输入,Ψξ和Θξ分别为离散系统的状态转移矩阵和输入矩阵.考虑到车辆动力学模型的复杂性,控制器设计中引入了约束条件,在目标函数中加入了松弛因子.在模型预测控制器的运行过程中,通过最小化跟踪误差和控制输入的消耗,实时计算最优解以获得最佳的车辆轨迹跟踪效果.目标函数可表示为
(15)
式中,Δη(k+j|k)为实际系统状态与参考系统状态之间的跟踪误差;Δu(k+j|k)为控制增量;ε为松弛因子;q1、q2、q3皆为权重系数.模型预测控制器计算所得的前轮转角控制需求记为δfd.
2.3 基于未知输入观测器的前轮转角估计
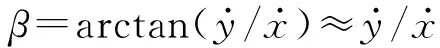
(16)
式(16)中车辆动力学模型的状态空间方程可表示为
yv=Cxv
(17)

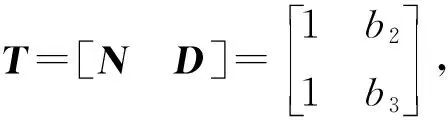
(18)

(19)
(20)
可知解耦后的子系统(19)中不含未知输入.此时系统的输入方程可表示为
(21)
(22)
(23)
由式(19)和式(23)可得
(24)

(25)

2.4 前轮转角跟踪控制
汽车转向机构是一个非线性、强耦合系统.为使跟踪误差快速收敛且有效避免奇异性问题,采用非奇异终端滑模控制设计非线性误差反馈控制律.可将式(11)可表示为
(26)

s=x1+k1x2k2
(27)
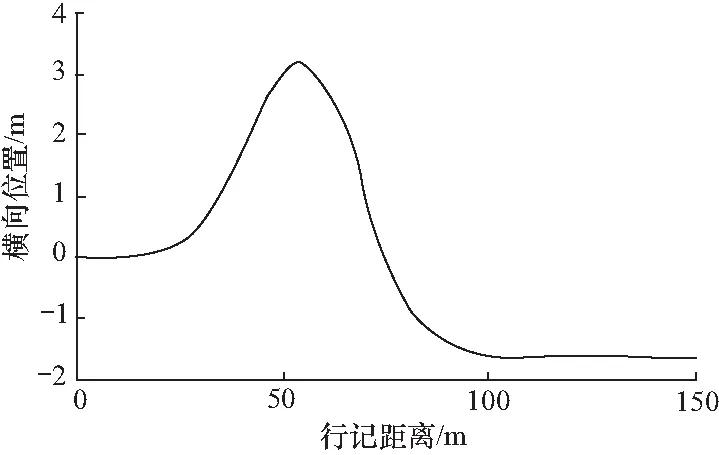
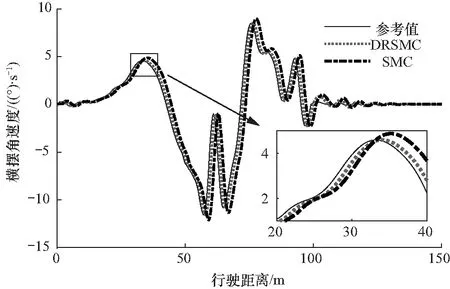
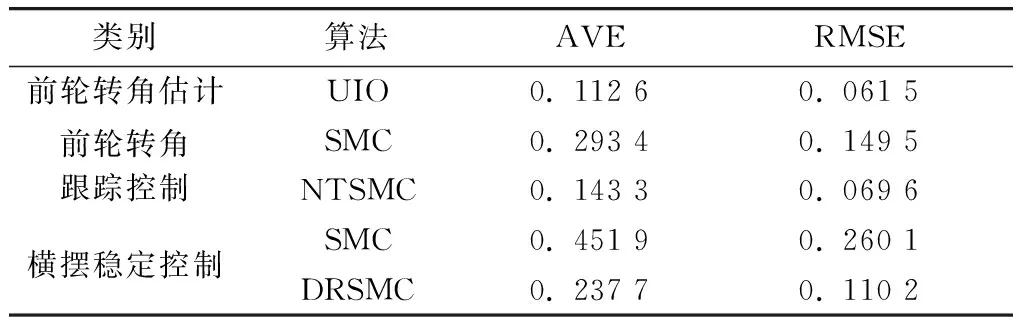
式中,k1和k2为调节参数,k1>0,1 uc=ue+uf (28) 式中:ue为等效控制项;uf反馈控制项. 为使系统状态在有限时间内趋近滑模面并沿滑模面收敛到期望值,对滑模面求导可得 (29) (30) 为了提高滑模运动的趋近效果并减小抖振,选择如下的指数趋近律 (31) 式中,l1和l2为大于0的参数. 根据式(30)和式(31),可得滑模控制率为 (32) 为证明所设计的滑模控制律能使系统在有限时间内收敛到0,选择Lyapunov函数为V=0.5ssT. 对Lyapunov函数求导可得 (33) 为实现车辆横摆稳定控制,考虑由轮胎力作用产生的横摆力矩,则可将式(3)表示为 (34) 联立式(34)和式(5)、(6),可得 (35) (36) 式中,p1>1,0 (37) (-kv1|sv|p1-kv2|sv|p2)≤0 (38) 从而证明了基于滑模的车辆横摆控制器的稳定性. 为了验证所提出的基于状态估计的车辆轨迹跟踪与横摆稳定协调控制策略,搭建了CarSim-Simulink联合仿真环境并进行了仿真测试,其中,利用CarSim软件提供车辆动力学模型,对应所提出的估计方法和车辆协调控制策略利用Simulink软件建立相应模型,车辆参数如表1所示. 仿真中,选用的双移线换道参考轨迹可表示为 表1 车辆仿真参数Tab.1 Vehicle simulation parameters (39) 图4 参考轨迹Fig.4 Referenced trajectory 利用未知输入观测器所得的车辆前轮转角估计结果如图5所示. 可以看出,前轮转角估计效果,满足车辆控制需求,从而可视为准确可靠的伪量测信息作为控制输入量. 图6所示为车辆转向控制结果. 为了充分反映所提出的非奇异终端滑模控制器(NTSMC)的实际效果,将常用的趋近律滑模控制(SMC)方法作为对比. 图6(a)中为两种不同控制方法下的前轮转向角,其中参考前轮转向角是先前基于MPC的轨迹跟踪控制器的计算结果,并用作车辆转向控制的控制目标. 根据局部放大图可知,车辆刚开始行驶时前轮转角波动较大但快速趋于收敛,振幅减小. 相比NTSMC,SMC控制下前轮转角波动收敛速度相对较慢,这将对车辆的航向控制产生影响. SMC控制下前轮转向角控制效果相比NTSMC也有些许滞后,整体控制精度NTSMC更高. 图6(b)所示为电机转向扭矩. 与NTSMC相比,SMC控制下电机的转向扭矩也相对滞后. 值得注意的是,在车辆开始运行时,NTSMC的电机转向扭矩小于SMC,这是因为NTSMC的收敛速度更快,波动时间相对较短,对车辆转向控制的不良抖动影响也更低. 图7所示为车辆横摆稳定性控制仿真结果. 为了验证所提出的基于双幂次趋近率滑模控制器(DRSMC)的效果,选用趋近律滑模控制方法作为对比. 结果表明,两种方法都能实现车辆参考横摆角速度的跟踪,但DRSMC的跟踪效果优于SMC,跟踪的实时性和准确性都得到了提升. 图5 前轮转角估计Fig.5 Results of front-wheel steering angle estimation 图6 车辆转向控制结果Fig.6 Results of vehicle steering control 图7 车辆横摆稳定控制结果Fig.7 Results of vehicle yaw stability control 为了进一步地体现文中方法的仿真效果,采用数据统计的方式定量化地表征不同控制方法下参考值和实际值之间的跟踪误差. 选用误差的平均值(average value of error, AVE)和均方差(root-mean-square error, RMSE)来反映对误差的控制效果,其表达式可写为 (40) (41) 式中:N为采样数;xk-A为第k个采样点的实际值;xk-R为第k个采样点的参考值.xk-A和xk-R皆分别对应着图5、图6(a)以及图7中的车辆状态量. 可知AVE体现了整体误差的大小,而RMSE体现了整体误差的波动情况,这两项指标可较好地反映误差控制水平. 所得的AVE和RMSE对比结果如表2所示. 由表2可知,文中方法的估计误差和控制误差整体来说都相对较小,表明对参考值的跟踪控制效果得以保证. 同时,相比SMC,所设计的NTSMC和DRSMC的AVE和RMSE相对来说都更小,表明上述的改进滑模控制方法对于整体的误差大小和误差波动都具有更好的抑制效果,有助于进一步地提高整车控制表现. 表2 AVE和RMSE对比结果Tab.2 Comparison results of AVE and RMSE 针对无人车轨迹跟踪控制问题,设计了一种基于状态估计的前轮转角跟踪和横摆稳定协调控制方法,在实现轨迹跟踪同时确保车辆横摆稳定. 利用模型预测控制算法设计了轨迹跟踪控制器,通过实时控制横向偏差和航向偏差来跟踪参考轨迹,得到参考前轮转角. 基于非奇异终端滑模控制设计了前轮转角控制器,通过转向的电机扭矩控制实现车辆转向. 考虑到前轮转角实际值难以直接测量,基于未知输入观测器设计了一种前轮转角估计方法,将估计结果视为伪量测值作为前轮转角控制器输入. 基于CarSim-Simulink联合仿真平台进行了仿真测试,结果表明,前轮转角估计精度较高可为控制器提供稳定可靠输入,协调控制策略能够在保证车辆横摆稳定性的同时使得车辆良好地完成双移线换道操纵.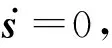

2.5 车辆横摆控制
3 仿真验证

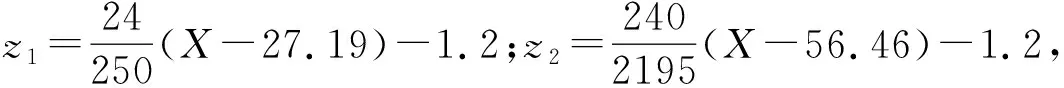

4 结 论
