嵌入控制油腔的静压滑动轴承可控性研究

陈淑江， 孙嘉珩

(山东大学 机械工程学院, 高效洁净机械制造教育部重点实验室，山东，济南 250061)

随着高精度产品对精密超精密机床加工精度要求的不断提升，静压主轴的回转精度亟待提高，固定节流的液体静压轴承已不能满足产品精度要求[1]. 主动节流技术是在传统可变节流器的基础上引入主动控制技术，可以主动改变润滑油流经节流器后的流量或压力，显著提高液体静压轴承的承载能力和油膜刚度，在工程上已得到证实[2-3].YANG等[4]研究了基于PID控制电液伺服阀的液体静压主轴的动态特性，结果表明采用PID控制的电液伺服阀能有效地提高轴承的动态特性和主轴的位置精度. PARK等[5]基于位移误差补偿原理，采用主动薄膜反馈阀实现了对导轨位移的主动控制，并取得了良好的效果. RENN等[6]基于主动控制的静压轴承，提出了一种由主动隔膜控制节流器的设计方案，通过伺服阀实现了静压轴承油膜间隙的精确闭环控制. 刘自超等[7]研究了压电致动薄膜反馈静压主轴的工作特性，结果表明压电致动薄膜反馈节流器能有效地提高静压主轴的轴承油膜刚度和主轴回转精度.胡灿等[8]研究发现主动节流技术相比于固定节流可以显著缩短轴心轨迹的过渡过程响应时间、减小轴颈偏心位移、降低主轴稳态回转误差.

上述主动控制节流技术通过调节节流器的节流特性，以优化轴承的油膜刚度和主轴的回转精度，取得了良好的效果，但其主轴运动可控性和稳定性还较差，提高主轴轴心运动的回转精度和控制效率变得尤为重要. 为达到这个目标，在传统4油腔静压轴承的每个油腔内，嵌套了一个较小面积的控制油腔，并采用主动单面薄膜节流器对其供油，充分利用轴承内部的二次节流，实现轴承的高刚度、低阻尼和良好可控性的并存. 针对该轴承建立了动态轴心轨迹的计算模型，采用有限差分法和欧拉迭代法求解了主轴的动态轴心运动，分析结构参数和供油参数对静压轴承的控制特性和动态特性的影响，并揭示其作用机理，藉此优化轴承结构.

1 轴承结构及工作原理

1.1 轴承结构

图1为嵌入控制油腔静压轴承的结构. 轴承有4个较大面积的承载油腔，与传统的静压轴承油腔结构对比，该轴承每个承载油腔内嵌套了一个较小面积的油腔，为控制油腔. 为降低各个油腔间流量交互造成的耦合影响，减弱油腔承载力的非线性，每2个相邻的承载油腔由轴向回油槽隔开，使各油腔独立. 除研究参数外，文中轴承结构参数及供油参数见表1.

图1 嵌入控制油腔静压轴承的结构Fig.1 Structure of the hydrostatic bearing with pressure control cavity

表1 轴承结构参数及供油参数Tab.1 Parameters of bearing structure and oil supply

图2为节流器与轴承的连接和供油方式. 上方和左方的控制油腔采用主动伺服节流器(可控节流器1、2)以较高的进油压力psc来供油，而右下的控制油腔使用固定液阻的节流器(固定节流器3、4)；此外，由固定节流器5、6、7、8对4个的承载油腔供油，进油压力为较低的ps，油腔压力分段线性压力分布如图3所示.

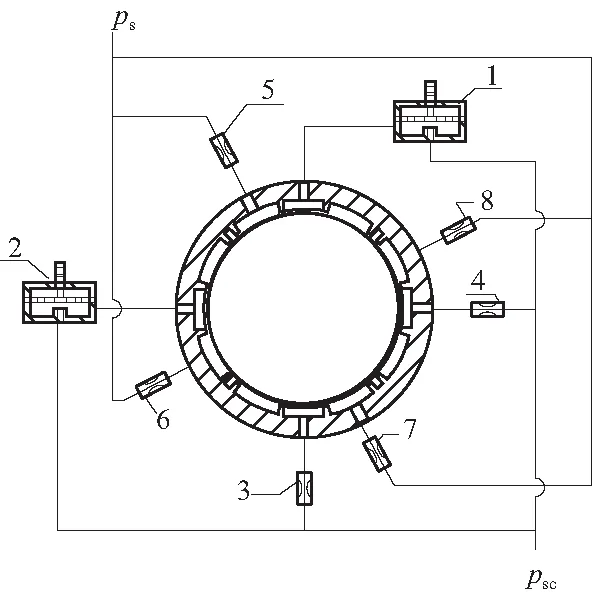
图2 供油方式Fig.2 Oil supply schematic diagram

图3 油腔压强分段线性分布示意图Fig.3 The piecewise linear diagram of pressure distrubution in oil cavity

1.2 伺服阀工作原理

图4所示为本文所选的用于主动控制的薄膜节流器(图2中可控节流器1、2)的原理图[7]. 通过给压电陶瓷施加电压，顶杆伸长，推动薄膜向下变形，使上方出油口的压力增加，下方出油口的压力减小，形成压差；减小电压时，薄膜在自身刚度的作用下恢复. 由于事先压电陶瓷有预伸长，薄膜不仅能恢复到平衡位置，而且能向上变形，使上下出油口形成一个反向压差. 这样通过调整输入电压改变节流间隙，进而改变对应控制油腔的腔内压力，可以使主轴作竖直方向和水平方向的运动.

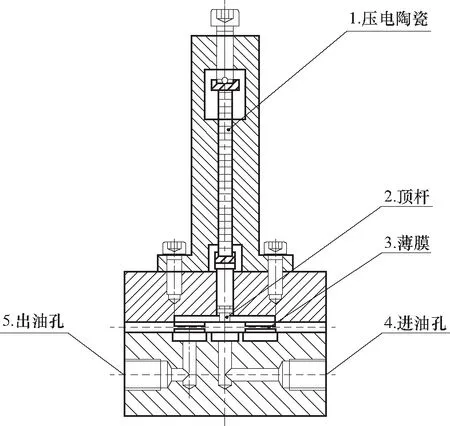
图4 伺服节流器原理图Fig.4 Servo restrictor schematic diagram

2 静压主轴轴心轨迹模型

2.1 静压主轴受力模型

由图5对静压主轴的受力进行计算，轴以角速度ω0逆时针方向旋转，Oj为主轴的几何中心，以轴承的几何中心O建立直角坐标系xOy，轴心位置坐标(x，y)，t为时间，Fi为油膜力在i方向上的分量，Li为外载荷在i方向的分量(i=x，y)，Mg为主轴自重，则任意时刻主轴运动方程为

图5 主轴受力计算模型Fig.5 Stress calculation model of the hydrostatic spindle

(1)

2.2 动态雷诺方程

用于求解不可压缩流体的径向静压滑动轴承的雷诺方程为

(2)

式中:θ为周向角度坐标;z为轴向坐标，ω0为主轴转速；μ为润滑油黏度；p为油膜压力. 计算时，取圆周方向油膜破裂的边界处油膜的压力及其一阶导数为0.

2.3 流量守恒方程

图中，qVci为控制油腔在4个封油边流出的流量，qVi为承载油腔在4个封油边流出的流量(i=1～4，分别为左、右、上、下方向封油边流出的流量)，qV、qVc为控制油腔、承载油腔由于挤膜效应产生的

图6 油腔内部流量矢量图Fig.6 Vector diagram of the oil cavity internal flow

体积流量，经过节流器对控制油腔供油的流量为qVcin，节流器对承载油腔供油的流量为qVin.

单位时间内，同时通过控制油腔的4个封油边，其流出流量为qVci，根据流量守恒方程，同一时间内，流进控制油腔的流量等于其流出流量，有

qVcin=qVc1+qVc2+qVc3+qVc4+qVc

(3)

从控制油腔流出的流量流入了较大面积的承载油腔，其数值大小等于同一时间段内流入的流量，同时承载油腔通过固定节流器供油，所以单位时间内，流进承载油腔的流量为qVcin及qVin，而流出的流量为qVi，有

qVcin+qVin=qV1+qV2+qV3+qV4+qV

(4)

考虑轴的转速，以逆时针旋转为例，对于控制油腔，单位时间内，其周向封油边的流量大小(以流出为正)为

(5)

其轴向上下封油边流出的流量为

(6)

由于油膜挤压效应从控制体流出的流量为

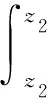
(7)

对于承载油腔，其周向封油边的流量为

(8)

其轴向上下封油边流出的流量为

(9)

由于油膜挤压效应从控制体流出的流量为

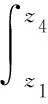
(10)

2.4 薄膜节流器流量及薄膜受力分析

2.4.1节流器流量计算

图7为压电陶瓷驱动单面薄膜节流器的工作模型，结构参数见表2. 主动单面薄膜节流器的节流区域属于环形平面缝隙流，节流区域的压力分布受油膜挤压效应的影响，可由雷诺方程求解. 可知主动单面薄膜节流器的流量公式为(取r=r2过流截面计算)[9]

表2 薄膜节流器结构参数Tab.2 Parameters of the membrane restrictor structural

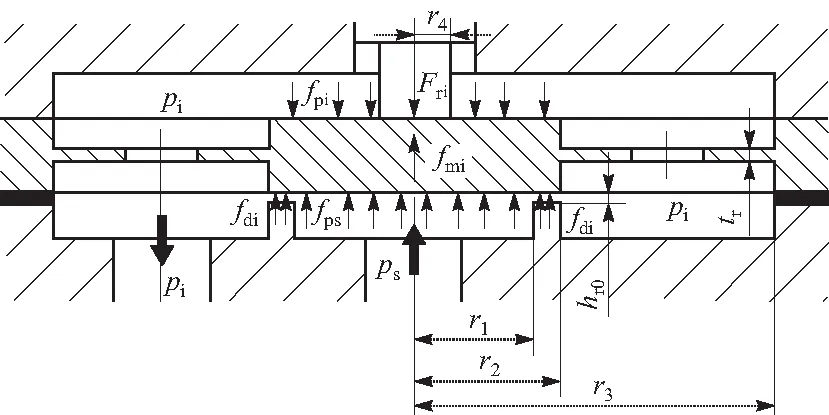
图7 压电陶瓷驱动单面薄膜节流器的工作模型Fig.7 Working model of the single-side membrane restrictor driven by piezoelectric ceramics

(11)

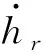
2.4.2节流间隙计算

根据图7，薄膜主要受到压电陶瓷的推力、自身变形力和油膜压力，因薄膜质量较轻，忽略自身重力.

① 设薄膜位移与压电陶瓷伸长量xe，则薄膜变形力为

fmi=kmxe

(12)

② 薄膜两侧压力.

上方岛型区压力为

(13)

下方进油区压力为

(14)

薄膜上下方压力和面积相等的区域受力相互抵消，不予计算；节流区的压力按压力分布进行积分计算,节流区压力为

(15)

③ 对薄膜进行受力分析，可得压电陶瓷的推力为

Fe=-fpi+fmi+fpi+fdi

(16)

④ 忽略对节流间隙影响较小的压电陶瓷的迟滞效性，压电陶瓷伸长量为

xe=U/k1-Fe/k2

(17)

式中：U为压电陶瓷施加电压；k1为介电常数；k2为刚度系数.

⑤ 节流间隙为初始节流间隙与压电陶瓷伸长量的差为

hr=hr0-xe

(18)

3 主轴轴心运动计算的欧拉方法

计算静压主轴的轴心运动需要同时求解雷诺方程和动力学方程，由初始条件可计算得油膜压力分布，积分可得油膜承载力，量纲一形式的计算公式如下.

(19)

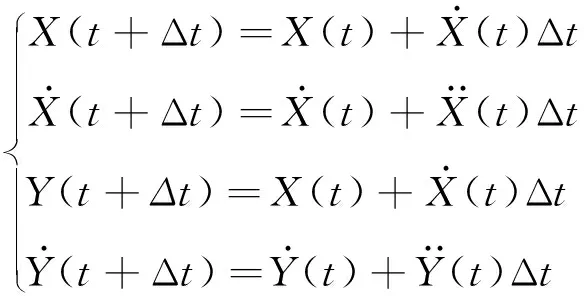
(20)

用欧拉法进行迭代，直到轴心轨迹收敛，取控制油腔进油压力psc=3 MPa，承载油腔进油压力ps=2 MPa，转速n0=2 500 r/min，计算时间0.4 s，Δt=10-5s进行仿真. 计算时，认为轴的质量分布均衡，在伺服阀压电陶瓷预紧电压Vx=Vy=20 V，仅重力作用下主轴轴心从轴颈和轴承的同心位置运动到平衡位置的动态发展过程如图8所示.

图8 轴心位置随时间的变化Fig.8 The change of spindle center position with time

4 轴承参数对动态特性及控制特性的影响

由于轴承的结构具有中心对称性，故只需对x或y其中一个方向进行研究，本文考虑选取x方向，研究姿态角α=0°的情况，等同于研究y方向，姿态角α=90°的情况，此时偏心率ε=x/h0. 计算时，取伺服阀压电陶瓷的预紧电压20 V，此时伺服节流阀的薄膜位置约为薄膜初始间隙的95%，此间隙薄膜节流器的液阻大致与对置的固定节流器液阻相同，便于进一步的研究和分析.

4.1 控制油腔面积占比的影响

由于控制油腔与承载油腔的腔内压力不同，控制油腔面积Sc相对于承载油腔的面积Sn的占比比率γ(γ=Sc/Sn×100%)会影响轴承的动静态特性，是影响轴承工作性能的重要参数之一.

4.1.1控制灵敏度

将控制灵敏度U定义为输出(轴心某个方向的位移)对单位输入(压电陶瓷施加电压)量的响应量

(21)

Uij为当轴心位置处于 (x0,y0) 时，单位输入电压Vj所能引起的油膜厚度在i方向分量的变化量(i，j=x或y)，反映了电压信号对主轴轴心运动控制的灵敏程度.

偏心率ε=0时，保持控制油腔的长宽比不变，控制灵敏度Uxx及Uyx随控制油腔面积占比比率γ的变化情况如图9所示.

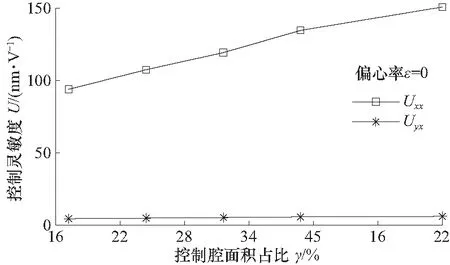
图9 控制灵敏度随控制油腔面积占比的变化Fig.9 The control-sensitivity for different area ratio of the control cavity

可以看出，Uxx随着γ的增大而增大，原因是控制油腔直接受薄膜节流器供油，控制油腔的面积越大，相同的微小输入量dV，会让油腔平均承载力有更大的改变.Uyx表示控制x方向的伺服阀输入电压引起的y方向油膜厚度的变化量，其数值相比于Uxx来说很小，原因是：本轴承具有4个回油槽将4个承载油腔分隔开来，降低了x与y方向控制效果的耦合影响，即x方向的伺服阀的输入对y方向轴心运动的影响很小，体现了该系统对x或y单方向轴心运动控制的有效性和精确性.

4.1.2刚 度

通常刚度越大，其抵抗外界干扰载荷的能力越强，回转精度也越高.

由图10可知，正刚度Kxx随偏心率绝对值|ε|的增大而减小，ε接近于0处时，Kxx取得最大值；相同偏心率下，控制油腔面积占比率γ越大，相同偏心下其刚度也越大，有助于系统抵抗外界各种干扰载荷，主轴回转精度会有所提升.

图10 不同控制油腔面积占比下正刚度随偏心率的变化Fig.10 The stiffness with the eccentricity for different area ratio of the control cavity

结合图10，由图11可以看出，交叉刚度Kyx相比于正刚度Kxx的数值(数量级)很小，说明轴承结构有效降低了x与y方向的耦合关系，减弱了油腔承载力的非线性. 与正刚度变化趋势相反的是，控制油腔面积占比的值γ越大，交叉刚度的数值越小，这是因为微小位移dx主要引起的是x方向控制油腔的瞬时液阻的变化，承载液阻的变化较小，而对y方向控制油腔和承载油腔液阻的影响情况则相反.

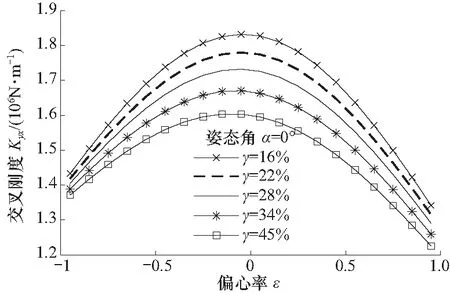
图11 不同控制油腔面积占比下交叉刚度随偏心率的变化Fig.11 The cross stiffness with the eccentricity for different area ratio of the control cavity

4.1.3阻 尼

由图12可知，阻尼随偏心率绝对值|ε|的增大而减小，在偏心率ε接近于0时阻尼达到最大；控制油腔面积占比率γ越大，相同偏心下阻尼Cxx越小. 综合刚度阻尼及控制灵敏度来看，当控制腔面积在30%左右时，其刚度较为适中且阻尼不会过大，而控制灵敏度也较为适中，此时系统动态特性和控制特性均较为优秀.

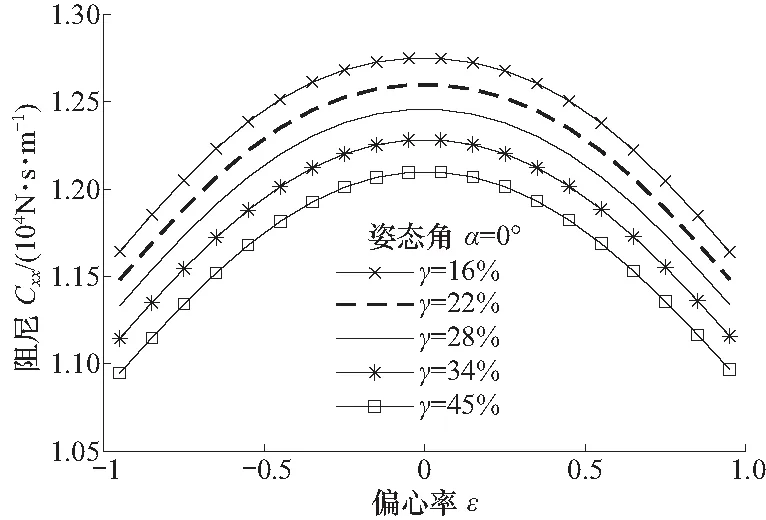
图12 不同控制油腔面积占比下阻尼随偏心率的变化Fig.12 The damping with the eccentricity for different area ratio of the control cavity

4.2 控制油腔封油边宽度的影响

同一偏心情况下，封油边宽度越大，油腔的瞬时液阻也就越大. 封油边宽度影响系统的液阻比进而影响节流比，由于两个腔的腔内压力不同，轴承的封油边宽度会影响同一偏心下的控制灵敏度、油膜刚度和阻尼.

4.2.1控制灵敏度

图13是偏心率ε=0时，控制灵敏度随封油边宽度的变化. 控制灵敏度Uxx随着封油边宽度a的增大而减小，原因是：该系统的节流比及液阻比发生了改变，封油边的宽度越大，相当于控制油腔的瞬态液阻Rc越大，因此同样的输入条件下，其流量的变化量会变小，轴承油腔的承载力变化也会变小，从而Uxx的值减小.Uyx的变化趋势与Uxx一致,其数值较小的原因已在4.1.1中分析，在此不做赘述.

图13 控制灵敏度随控制油腔封油边宽度的变化Fig.13 The control-sensitivity for different witdh of the bearing land

4.2.2刚 度

由图14可以看出，刚度Kxx随偏心率ε的变化而变化，当-0.44<ε<0.44时，封油边宽度a越大，刚度也越大，而当ε<-0.48或ε>0.48时，封油边的宽度越大，刚度越小；封油边的宽度越大，刚度随着偏心波动的幅度也会越大；图15为ε=0和ε=80%时刚度随封油边宽度的变化情况，在ε=0时，封油边宽度在5 mm处取得了最佳刚度，在ε=80%时，刚度随封油边宽度的增加而减小.偏心率很大情况下，封油边宽度较小时(2 mm)刚度更高，但静压轴承工作时属于完全流体润滑，偏心率很大的情况较少，故一般情况下，封油边宽度为5 mm时轴承对外界干扰载荷的抵抗能力更强，油膜承载能力也更大.

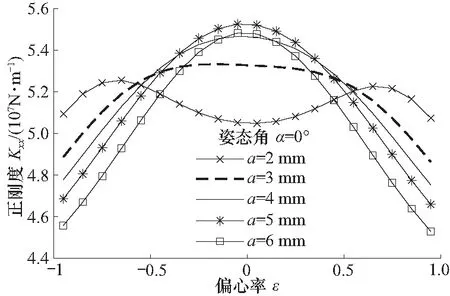
图14 不同控制油腔封油边宽度下刚度随偏心率的变化Fig.14 The stiffness with the eccentricity for different witdh of the bearing land

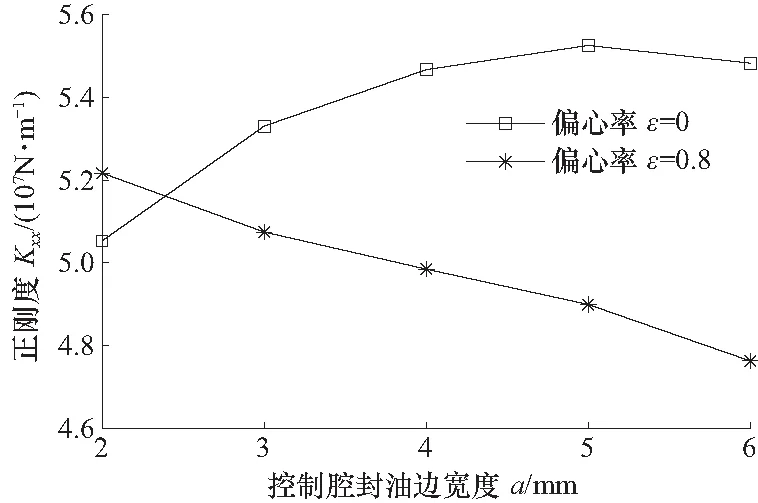
图15 不同偏心下刚度随封油边宽度的变化Fig.15 The stiffness for different witdh of the bearing land

由图16可以看出，随着偏心率绝对值|ε|的增大，交叉刚度Kxy呈减小趋势，而封油边宽度的变化对交叉刚度的影响程度较小，这是因为对y方向的油腔来说，x方向的微小位移dx主要引起的是y方向承载油腔的瞬时液阻的变化，而控制油腔液阻的变化较小，故虽然控制油腔封油边宽度改变，但交叉刚度并未改变太多.

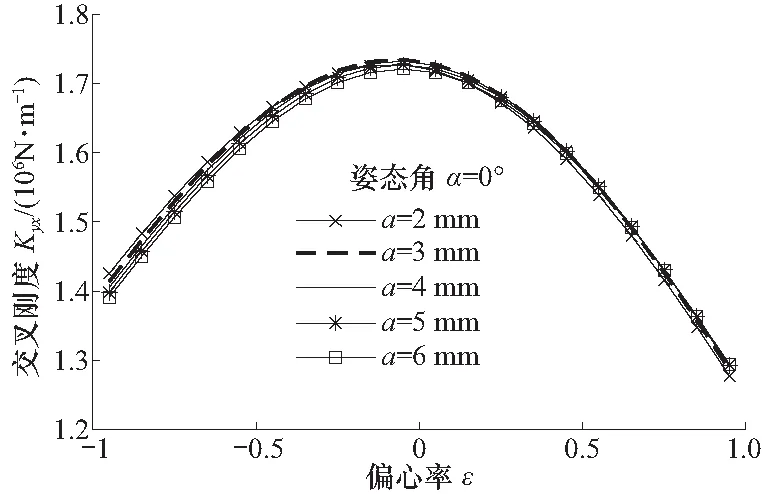
图16 不同控制油腔封油边宽度下交叉刚度随偏心率的变化Fig.16 The cross stiffness with the eccentricity for different witdh of the bearing land

4.2.3阻 尼

由图17可知，阻尼随偏心率绝对值的增大而减小，在偏心率趋近于0时阻尼达到最大；在偏心率绝对值较大时，封油边宽度a对阻尼的影响程度很小；在偏心率绝对值较小时，封油边宽度越大，相同偏心下阻尼越大. 综上，当封油边宽度在5 mm左右时，其刚度在偏心率为0时取得了极大值，而阻尼不会因封油边宽度变化有太大变化，控制灵敏度也较为适中，此时系统动态特性和控制特性均较为优秀.

图17 不同控制油腔封油边宽度下阻尼随偏心率的变化Fig.17 The damping with the eccentricity for different witdh of the bearing land

4.3 进油压力的影响

4.3.1控制灵敏度

图18是以承载油腔的进油压力ps为横坐标(控制油腔进油压力与承载油腔的进油压力比psc/ps=1.5，固定不变)，偏心率ε=0时控制灵敏度随进油压力的变化情况，可以看出进油压力的改变对Uxx及Uyx数值的影响很小，原因是：系统的液阻比并未改变，同样的输入条件下，造成轴承对置油腔承载力变化的差距值基本不变.

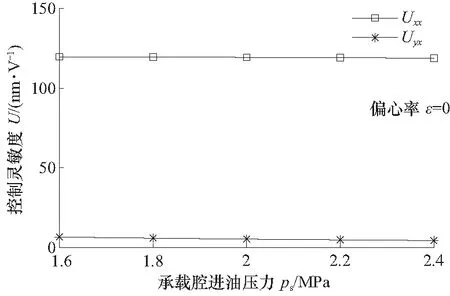
图18 控制灵敏度随进油压力的变化Fig.18 The control-sensitivity for different oil supply pressure

4.3.2刚 度

由图19可以看出，随偏心率绝对值的增大，刚度呈减小趋势；进油压力越大，刚度也越大(相同的偏心率下)，图20为偏心ε=0时，以承载油腔的进油压力ps为横坐标(控制油腔进油压力与承载油腔的进油压力psc/ps=1.5，固定不变)，刚度随进油压力的变化情况，随着进油压力的增大，刚度Kxx接近于线性增大，系统对外界干扰载荷的抵抗能力更强。

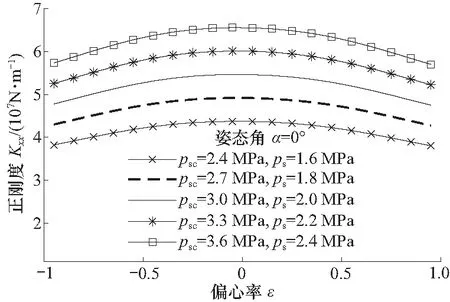
图19 不同进油压力下刚度随偏心率的变化Fig.19 The stiffness with the eccentricity for different oil supply pressure

图20 刚度随进油压力的变化Fig.20 The stiffness for different oil supply pressure

由图21可以看出，交叉刚度随偏心率绝对值的增大而减小，而进油压力的变化对交叉刚度的影响程度较小，原因是：该系统的液阻比并未改变，同样的输入条件下，轴承对置油腔的承载力差距大小基本不变.

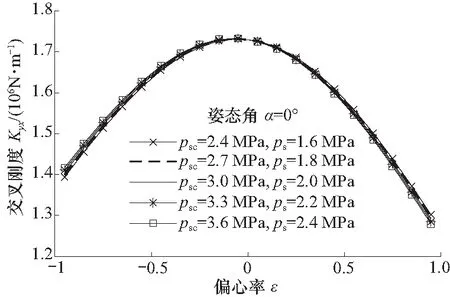
图21 不同进油压力下交叉刚度随偏心率的变化Fig.21 The cross stiffness with the eccentricity for different oil supply pressure

4.3.3阻 尼

由图22可以看出，阻尼随着偏心率的增大而减小，其整体波动幅度小于15%，在偏心率趋近于0时阻尼达到最大；进油压力对阻尼基本无影响，这是因为阻尼主要与润滑油黏度、油腔面积和油腔瞬时液阻大小有关，而与进油压力基本无关.

图22 不同进油压力下阻尼随偏心率的变化Fig.22 The damping with the eccentricity for different oil supply pressure

5 结 论

为提高静压主轴轴心运动的可控性和稳定性，本文针对嵌入控制油腔的液体静压轴承，采用有限差分法和欧拉迭代法建立了主轴轴心运动的动态模型，研究了不同轴承结构参数和进油压力下系统的控制特性及动态特性，得出了轴承结构参数的较优取值范围，结论如下：

① 当控制油腔相对整个油腔的面积占比增大时，控制灵敏度、刚度和阻尼随之增大，交叉刚度随之减小. 为平衡刚度和阻尼的关系，应选择较为适中的控制油腔面积占比，当控制油腔面积占比在30%附近，刚度、阻尼和控制灵敏度均较为优秀，此时系统同时具备良好的动态特性和控制特性.

② 封油边宽度对阻尼的总体影响程度较小. 控制油腔的封油边宽度增大时，控制灵敏度会随之减小；当-0.44<ε(偏心率)<0.44时，封油边宽度越大，刚度也越大，而当ε<-0.48或ε>0.48时，封油边的宽度越大，刚度越小. 封油边的宽度越大，刚度随着偏心率变化而波动的幅度也会越大，在ε=0时，当封油边宽度为5 mm取得了最佳刚度，阻尼和控制灵敏度均较为优秀，其刚度随偏心率变化的整体波动范围也较为适中，系统同时具备良好的动态特性和控制特性.

③ 进油压力越大，在相同偏心率下，刚度也越大；在偏心率ε=0时，正刚度随进油压力的增大基本呈线性增大；但进油压力对控制灵敏度、交叉刚度和系统阻尼的影响程度较小.