非平衡力作用下有质量弹簧伸长量的确定

2021-11-08安徽王伟民

教学考试(高考物理) 2021年5期

安徽王伟民王坤

在弹性限度内，弹簧的形变量与所受的外力成正比，这是胡克定律的内容，其数学表达式为F=kx(k为弹簧的劲度系数)。对确定的弹簧而言，其劲度系数为常量。利用该定律，我们可以根据所受外力和已知的弹簧的伸长量方便的计算劲度系数(当然，也可以变换已知条件计算其他相关的未知物理量，比如根据已知条件，确定弹簧的原长、弹簧的总长或弹簧所受外力的大小等)。

需要说明的是，对该类问题，人们探讨较多的是在弹簧受平衡力作用、保持平衡状态情况下相关未知量的求解。那么，如果弹簧在非平衡力的作用下，弹簧将处于非平衡状态，与弹簧有关的未知物理量的求解应如何进行？

【例1】如图1所示，一劲度系数为k=150 N·m-1的弹簧放在光滑水平面上，在其两端分别施加大小为F1=7 N和F2=5 N的两个力，二力反向且共线，求稳定之后弹簧的伸长量？

图1

【分析】因为弹簧两边受到的拉力大小不等，所以，在两端拉力作用下弹簧会沿拉力大的F1的方向向左加速运动。如果从某点把弹簧分成左右两部分，那么，稳定之后弹簧左边的部分在“拉”着右边的部分向左加速。对右段弹簧进行受力分析并结合牛顿第二定律可知，左段弹簧对右段弹簧的拉力，等于右段弹簧的质量与其加速度的乘积再加上整个弹簧右端所受的拉力F2，由于稳定后弹簧各位置的加速度相同，所以，弹簧上越靠近左端的点，其右侧的弹簧总质量便越大，该点弹簧的弹力就越大，因此，从整体来看，弹簧的伸长是不均匀的——如果把弹簧分成长度相等的若干部分(指弹簧不受力情况下的等分，即对原长进行等分)，那么原长相等的各部分，稳定之后越靠近左边的部分伸长量越大。

图2

在两端各受到与该弹力大小相等的拉力的作用下，微元弹簧的伸长量dL为：

因此，在两边拉力F1和F2作用下，弹簧稳定之后整个弹簧的伸长量ΔL为：

=0.04 m

答：稳定之后弹簧的伸长量为0.04 m。

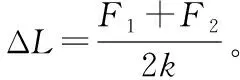
显然，这种情况下弹簧的形变情形等效于惯性参考系中自身具有重力的弹簧上端固定，下面悬挂重物而静止的情形——在非惯性参考系中，例1所给问题中的弹簧“重力”大小为(之所以将“重力”二字加引号，是因为这里的“重力”指的是“等效重力”，方向不是竖直向下，而是水平向右)F1-F2，弹簧右端“悬挂”“重力”大小为F2的物体，易知，在此情况下弹簧的伸长量为：

可以发现，这个结果与上面采用积分的方法推理出的结果是一样的。