从“无模到有模、有模到有法”突破电磁感应中的单棒问题

2021-11-08湖南王经天丁学农

教学考试(高考物理) 2021年5期

湖南王经天丁学农

在平时的教学中，通常是分类“建模”去处理电磁感应中的单棒问题，例如“R-v0”型、“R-F”型、“E-R”型、“C-F”型等等。“建模”法处理电磁感应中的单棒问题的优势是学生模仿快、短期效果明显，但在实际应用中的劣势是不能以不变应万变，学生遇到新的问题往往无法下手。在“建模”之前先让学生形成思想方法，让学生实现从“无模”到“有模”的过渡，在实践的过程中再让学生实现“有模”到“有法”的升华，这样才能真正帮助学生突破电磁感应中的单棒问题。

一、“无模”到“有模”

1.情景构建：如图1所示，有一垂直于倾角为θ的平行金属导轨MN和PQ向下的匀强磁场，磁场的磁感应强度为B，平行导轨MN和PQ间的距离为L，导轨的NQ之间接有电阻R，在导轨上静止释放与导轨垂直的电阻为r、质量为m、长度也为L的金属棒ab，ab棒和导轨接触良好，ab棒和导轨间的动摩擦因数为μ，导轨电阻不计，导轨足够长，重力加速度为g。

图1

2.过程体验：

(1)“转化图形”——把立体图转化为平面图便于对棒进行受力分析

(2)“判断流向”——利用右手定则判断出导体棒ab中的电流I由a→b，为棒的受力分析服务

(3)“受力分析”——ab棒的受力情况如图2所示

图2

受力分析的目的是：

②若导体棒处在变速状态，根据牛顿第二定律建立方程，得出导体棒的加速度a的表达式

③若导体棒处在平衡状态，则建平衡方程

(4)“过程分析”——画出v-t图像

图3

(5)“能量分析”

假设ab由静止释放到达到最大速度过程中沿导轨下滑的位移为x，求电路中产生的总热量Q?

①方法一：根据焦耳定律Q=I2Rt求解，由于在ab棒加速下滑过程中，电路中的电流是变化的，因此在此情景中不能用焦耳定律求电路中产生的热量

②方法二：用动能定理求解

WF安=Q

③方法三：根据能量守恒定律求解

(6)“动量分析”

①已知导体棒ab从静止释放到达到最大速度过程中，沿导轨下滑的位移为x，求流过电阻R的电荷量q？

②已知导体棒ab从静止释放到达到最大速度过程中，流过电阻R的电荷量为q，求此过程所用时间t？

对导体棒ab由动量定理得：沿斜面向下方向为正方向，

mgsinθ·t-μmgcosθ·t-BLIt=mvm

即mgsinθ·t-μmgcosθ·t-BLq=mvm

注意：已知导体棒ab从静止释放，到达到最大速度过程中，沿导轨下滑的位移为x，就可求出此过程中流过电阻R的电荷量q，求出了电荷量q，再根据动量定理就可求出此过程所对应的时间t，一般在情景中出现了q、x、t三个物理量往往需要考虑从动量定理入手分析。

3.方法总结

说明：电磁感应中的单棒问题的思路如上方法总结，但是在实际应用中往往要根据题中的实际情况合理选择切入点。

二、“有模”到“有法”

建模说法一：“R-v0”型

【例1】(多选)如图4所示，两根足够长的平行金属导轨相距为L，其中NO1、NO2部分水平，倾斜部分MN、PQ与水平面的夹角为α，整个空间存在磁感应强度为B的匀强磁场，磁场方向垂直导轨平面MNQP向上，长为L的金属棒ab、cd与导轨垂直放置且接触良好，其中ab光滑，cd粗糙，棒的质量均为m、电阻均为R。将ab由静止释放，在ab下滑至速度刚好达到稳定的过程中，cd始终静止不动。若导轨电阻不计，重力加速度为g，则在上述过程中

图4

( )

A.ab棒做加速度减小的加速运动

C.cd棒所受摩擦力的最大值为mgsinαcosα

D.cd中产生的热量等于ab棒机械能的减少量

【解析】①“转化图形”：把立体图转化为平面图

②“判断流向”：由右手定则判断ab棒中的电流由b流向a

③“受力分析”和“过程分析”：受力分析如图5

图5

对cd棒受力分析如图6，摩擦力等于安培力在水平方向的分力，即f=BILcosα=mgsinαcosα，C正确；

图6

④“能量分析”：由能量守恒可得，ab棒减小的机械能等于ab和cd产生的焦耳热，D错误。

【点评】本题充分体现了处理电磁感应中的“R-v0”型单棒问题的基本方法：转化图形→判断流向→受力分析→过程分析→能量分析

建模说法二：“R-F”型

【例2】(多选)如图7所示，光滑的平行竖直金属导轨AB、CD相距L，在A、C之间接一个阻值为R的电阻，在两导轨间abcd矩形区域内有垂直导轨平面向外、宽为5d的匀强磁场，磁感应强度为B，一质量为m、电阻为r，长度也刚好为L的导体棒放在磁场下边界ab上(与ab边重合)。现用一个竖直向上的力F拉导体棒，使它由静止开始运动，已知导体棒离开磁场前已开始做匀速直线运动，导体棒与导轨始终垂直且保持良好接触，导轨电阻不计，F随导体棒与初始位置的距离x变化的情况如图8所示，下列判断正确的是

图7

图8

( )

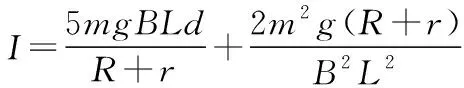
【解析】①“转化图形”：本题图为平面图，无需转化

②“流向判断”：据右手定则得电流由a流向b

③“受力分析”：对ab受力分析如图9

图9

⑤“能量分析”：ab棒从开始运动到离开磁场过程

其中WF=2mgd+3mg(5d-d)=14mgd

⑥“动量分析”：

对导体棒由动量定理得：I-BLq=mv

【点评】虽然【例2】和【例1】的模型不同，但处理方法是相同的。

建模说法三：“C-F”型

【例3】如图10，两条平行导轨所在平面与水平地面的夹角为θ，间距为L。导轨上端接有一平行板电容器，电容为C。导轨处于匀强磁场中，磁感应强度大小为B，方向垂直于导轨平面。在导轨上放置一质量为m的金属棒，棒可沿导轨下滑，且在下滑过程中保持与导轨垂直并良好接触。已知金属棒与导轨之间的动摩擦因数为μ，重力加速度大小为g。忽略所有电阻。让金属棒从导轨上端由静止开始下滑，求：金属棒的速度大小随时间变化的关系。

图10

【解析】①“转化图形”：平面图如图11所示

图11

②“流向判断”：如图11所示

③“受力分析”：如图11所示

对金属棒由牛顿第二定律：

mgsinθ-μmgcosθ-BLI=ma

【点评】“C-F”型单棒问题的难点在对棒的加速度的求解分析，需学生细致推敲。虽然相对“R-v0”型模型及“R-F”型模型的难度上升了不少，但处理“C-F”型单棒问题的方法依然是相同的，本题由于未涉及能量和动量问题，所以过程分析到位后本题实际上已完成。

建模说法四：“E-R”模型

【例4】如图12所示，长平行导轨PQ、MN光滑，相距L=0.5 m，处在同一水平面中，磁感应强度B=0.8 T的匀强磁场竖直向下穿过导轨面。横跨在导轨上的直导线ab的质量m=0.1 kg、电阻R=0.8 Ω，导轨电阻不计。导轨间通过开关S将电动势E=1.5 V、内电阻r=0.2 Ω的电池接在M、P两端，试计算分析：