材料Norton指数对空洞闭合行为与闭合规律的影响
2021-11-07张代杰尉珂瑞王天慧康红力赵泽旭谢臻轩
张代杰 尉珂瑞 王天慧 康红力 赵泽旭 谢臻轩
(太原科技大学材料科学与工程学院,山西030024)
随着我国工业日益壮大,装备制造业逐渐向高端化迈进,提高大型锻件的性能与质量是发展高端装备之关键[1-2]。很多高端装备基础件是由钢锭经锻造而制成,其生产加工过程主要包括冶炼、浇铸、锻造、热处理等工序。而钢锭在浇铸过程中容易存在缩孔、疏松等空洞缺陷[3- 4]。钢锭内部的空洞缺陷只有在后续的热变形过程中完全消除,才能获得高品质的高端装备零部件[5]。因此,探究钢锭内部空洞在变形过程中的闭合行为非常重要。
许多学者利用物理模拟与数值模拟方法对空洞的闭合行为进行了大量研究。蒋智等[6]利用有限元技术及带有人工空洞的PC试样的镦粗试验研究了空洞所在的位置对空洞闭合的影响,发现位于圆柱体心部的空洞比靠近圆柱体端面及侧表面的空洞更容易闭合。Hibbe等[7]利用ABAQUS数值模拟软件研究了AISI- 4137材料内部椭球体空洞的闭合行为,确定了椭球体空洞闭合所需的等效应变。Wang等[8]在大量数值模拟与理论计算的基础上,得到了应力三轴度、罗德参数以及等效应变对空洞闭合的影响机制,并建立了一种空洞闭合模型,同时使用AISI-1045钢作为物理模拟材料,研究了径向锻造过程中材料内部空洞的闭合行为,并对其提出的模型进行了验证。李殿中等[9]基于WRF锻造工艺,提出了单向大变形压实法,从数值模拟与实验验证两方面阐述了该工艺对于消除管板类锻件内部空洞的有效性与可靠性。
已有研究表明,数值模拟是研究空洞闭合的重要方法之一,它可以分析一定变形状态下空洞演变行为与演变规律。然而随着关于空洞闭合的研究日渐深入,有些学者发现材料的一些本质属性会通过影响塑性变形行为而影响空洞的闭合,并针对此问题进行了一些研究[10-11]。尽管如此,目前关于材料属性对空洞闭合行为的研究仍相对较少。因此,本文基于数值模拟技术,通过圆柱体单轴压缩数值模拟试验,系统地研究了材料Norton指数对空洞闭合规律的影响。
1 有限元模型
1.1 材料模型
金属材料在高温塑性变形时会表现出粘性,体现为材料的应力随应变速率的变化而改变,呈现出不可压缩非线性粘性材料的流动特征。材料的这种特征可用下述材料模型来表示[12-14]:
(1)
(2)
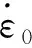

1.2 几何模型
单轴压缩数值模拟选取含有中心球形空洞的圆柱体工件,工件内部球形空洞的球心位于圆柱体的轴线上。由于圆柱体为回转体,选取1/4圆柱体进行数值模拟,圆柱体模型及上下平砧三维模型如图1所示。圆柱体锻件尺寸为∅20 mm×20 mm,中心空洞直径为∅2 mm。

图1 数值模拟几何模型Figure 1 Geometric model of numerical simulation
1.3 模型参数
模拟时,由于为单轴压缩变形,圆柱体试样与上、下砧间的剪切摩擦因子取0;上砧沿-Z方向的速度为1 mm/s;网格数为12 000个,并对空洞周围区域网格进行局部细化。
2 结果与讨论
2.1 球形空洞形状闭合过程
单轴压缩变形过程中,空洞随着变形的发生其形貌也会有所变化直至闭合。图2表示线性粘性材料(Norton指数n=1)在变形过程中,中心球形空洞在圆柱体试样子午面上的形貌变化。从图2可以看出,空洞在闭合过程中,其形状由球形逐渐变为椭球形,最后被压成一条缝隙,直至空洞闭合。

图2 变形过程中空洞形貌变化Figure 2 Evolution of void morphology during deformation
图3表示变形量为30%时,Norton指数n=1及n=5的两种材料构成的工件子午面上的内部空洞周围的等效应力σ的分布情况。从图中可以看出,空洞的存在对周围基体应力状态的影响具有区域性,空洞的应力影响区呈现类似花瓣状分布,空洞所在区域的应力影响区半径约为3倍的原始空洞半径。同时,等效应力σ的最大值在空洞长轴的端点附近区域,最小值在空洞短轴的端点附近区域。而材料Norton指数的变化对应力影响区形貌的影响不大,但对等效应力的大小影响十分明显。这是因为压缩过程中,上砧的压下速率为1 mm/s,工件的等效应变速率小于1 s-1。根据式(2)可知,Norton指数n越大,材料变形所需等效应力就越大。因此,Norton指数n=1的材料比n=5的材料变形所需等效应力更小。
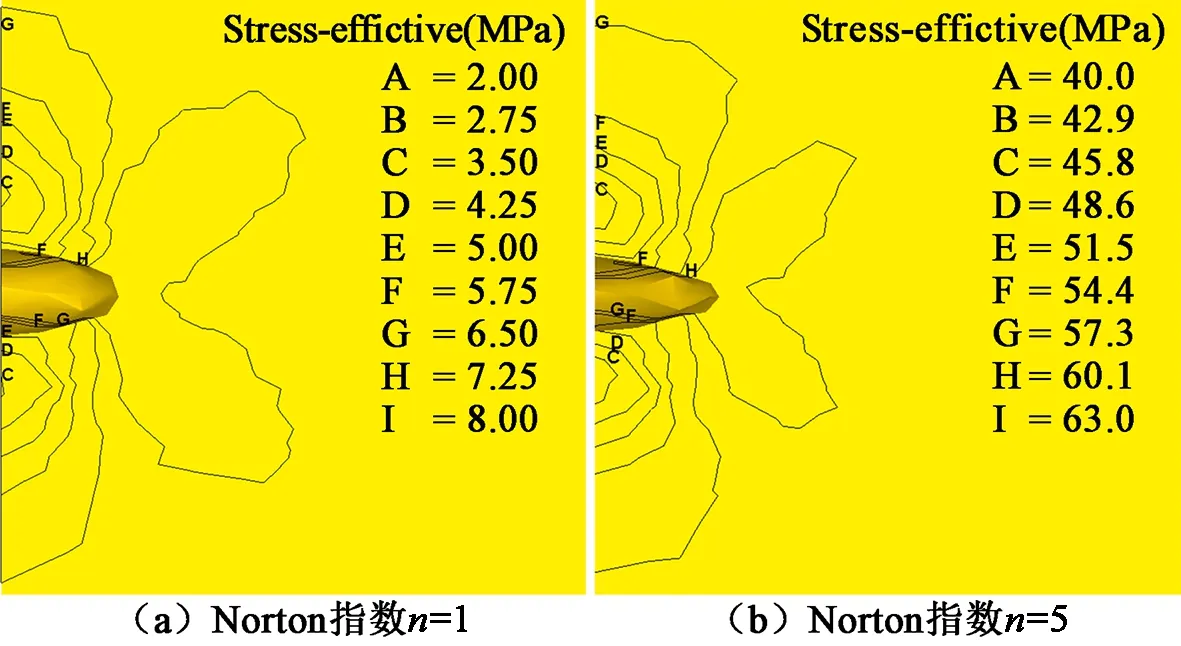
图3 变形量为30%时空洞对基体等效应力的影响Figure 3 The effect of voids on the equivalent stress of the matrix material when the deformation is 30%
图4表示变形量为30%时,Norton指数n=1及n=5的两种材料构成的工件子午面上的内部空洞周围的等效应变ε的分布情况。由图可知,空洞的存在对周围基体材料有影响,造成了应变的不均匀分布。对比图4(a)和(b)可知,材料Norton指数的变化对空洞周围应变分布影响不大,应变影响区范围与应力影响区相同,影响区形貌也呈现花瓣状分布。在整个子午面上,基体材料大部分区域的等效应变ε约为0.357。从图中还可以看出,等效应变ε的最大值在空洞长轴的端点附近区域,最小值在空洞短轴的端点附近区域,即空洞周围基体材料在空洞的短轴附近变形很小,而在长轴附近变形很大。然而值得注意的是,尽管等效应变ε的最小值也出现在空洞短轴的端点附近区域,但是Norton指数越大,短轴的端点附近区域的等效应变ε的值越小。

图4 变形量为30%时空洞对基体等效应变的影响Figure 4 The effect of voids on the equivalent strain of the matrix material when the deformation is 30%
2.2 材料Norton指数对空洞闭合的影响
材料Norton指数是衡量材料应力与应变速率关系的重要参数。当材料Norton指数n趋于+∞时,材料为理想刚塑性材料;当材料Norton指数n为1时,材料为线性粘性材料。材料Norton指数n对材料的变形有着重要的影响,故其对空洞的闭合过程也有所影响。根据单轴压缩数值模拟,分析了材料Norton指数n对空洞闭合的影响规律。为了方便研究,定义空洞形状系数为空洞短轴轴长与初始直径之比,即初始空洞形状系数为1,而空洞闭合时,空洞形状系数为0。
图5表示Norton指数n不同的材料在单轴压缩过程中,空洞形状系数随着变形量变化的演变规律。Norton指数n分别取1、2、5、10、100。由图可知,当变形量一定时,Norton指数n越大,空洞形状系数越小。空洞完全闭合时,即空洞形状系数为0时,Norton指数n越大,变形量也越小。可见,Norton指数n越大,空洞闭合所需变形量越小。而空洞形状系数的改变主要与空洞短轴端点的流动速度密切相关。

图5 Norton指数对空洞闭合的影响Figure 5 Effect of Norton index on voids closure
为方便研究,定义空洞边界上A点为空洞短轴的端点,B点为空洞长轴的端点,如图6所示。图7表示Norton指数n不同的材料在单轴压缩过程中,A点的相对速度随着变形量变化的演变规律。此相对速度是指在Z方向上,A点相对点B的速度。相对速度越快,空洞闭合的越快。从图中可以看出,A点的相对速度随着变形量的增加而增大;而在变形量相同的条件下,Norton指数n越大,A点的相对速度越快。

图6 空洞边界的取点位置Figure 6 The location of points on the boundary of a void
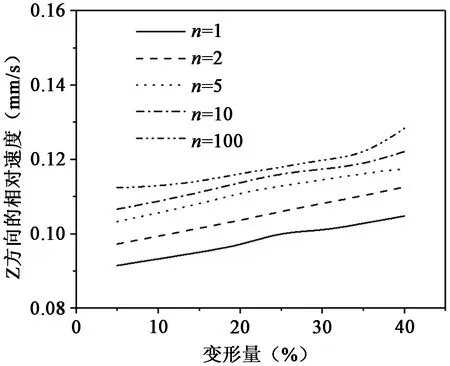
图7 相对速度分析Figure 7 Analysis of relative velocity
3 结论
基于单轴压缩数值模拟,通过研究工件内部空洞的演变行为,阐明了变形过程中材料Norton指数n对空洞演变情况的影响规律,并得到以下结论:
(1)空洞在闭合过程中,其形状由球形逐渐变为椭球形,最后被压成一条缝隙,直至空洞闭合。
(2)空洞的等效应力、等效应变影响区呈现花瓣状分布。材料Norton指数n的变化对等效应力、等效应变影响区的形貌的影响不大,但对等效应力的大小影响十分明显。
(3)在单轴压缩条件下,空洞短轴端点的相对速度随着变形量的增加而增大;而在变形量相同的条件下,Norton指数n越大,短轴端点的相对速度越大。因此,Norton指数n越大的材料,空洞闭合所需变形量越小。
