数控内齿强力珩齿珩削力的预测方法研究
2021-11-07刘海军
丁 恒, 夏 链, 韩 江, 刘海军
(合肥工业大学 机械工程学院,安徽 合肥 230009)
内齿珩轮强力珩齿相较于蜗杆砂轮磨齿具有重合度大、无齿面烧伤等优点[1],广泛应用于齿轮精加工工艺。其中珩削力的大小直接影响被珩工件的加工质量和成本。因此工程实践中往往希望获得珩削力的大小,以提高被珩工件的表面质量和降低加工成本。
文献[2]利用齿轮交错轴啮合原理推导出内珩轮齿面方程,为珩削力的研究奠定了理论基础;文献[3]对内齿珩轮强力珩齿加工工艺进行了较为系统的研究,提出一种基于响应曲面法来预测内齿强力珩齿加工误差;文献[4]推导了珩齿加工接触点上珩削速度的表达式,并通过试验得出了珩削速度与工件齿面质量之间的关系。随着珩削速度的增加,工件同一齿面的粗糙度值差异会增加;文献[5]设计了一个类比2个滑移运动的合成磨削装置来模拟外啮合珩削过程,进行低速磨削试验,进而得到磨削速度与磨削力之间的关系;文献[6]利用有限元进行微观珩削仿真计算接触线珩削力,并讨论珩削速度、进给量和砂轮表面状态对珩削力的影响。
直至目前,将数值模型(如指数型模型、神经网络)用于内齿强力珩齿珩削过程中珩削力预测的研究却鲜有报道。作为经典的切削力预测方法之一,数值模型在传统切削加工中发挥着不可替代的作用[7-9]。因此本文将数值模型引入到内齿强力珩齿加工中以探索珩削力的预测方法。
本文针对内齿珩轮强力珩齿加工工艺,以珩轮转速、珩轮径向进给量、珩轮轴向进给速度为设计因子展开珩削试验;然后应用反向传播(back propagation,BP)神经网络建立珩削力预测方法,并与传统的指数型模型预测结果进行对比,研究不同方法的预测精度和使用方便性,从而为内齿珩轮强力珩齿珩削力预测提供理论指导。
1 内啮合强力珩齿加工分析
1.1 内啮合强力珩齿整机模型
常见的内齿强力珩齿机床设备结构如图1所示。从图1可以看出,珩齿机有7个轴。
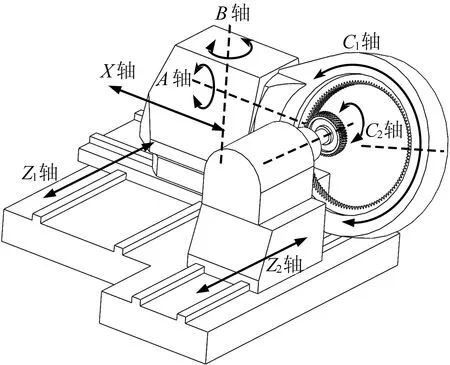
图1 内齿强力珩齿机结构
各轴作用见表1所列。内齿强力珩齿机床在珩削斜齿圆柱齿轮时,联动关系包括C1、C2、Z13根轴。A轴用来调节珩磨轮与工件齿轮之间的夹角。加工时,C2轴跟随C1轴和Z1轴的实时插补位置同步运动,珩轮沿着X轴逐步切削齿厚方向的余量,并沿着Z1轴切下整个齿宽。

表1 珩齿机各轴功能
1.2 珩削加工力学分析
内啮合珩齿运动过程是一对交错轴斜齿轮轴线呈一定的角度传动,工件齿轮和内齿珩轮被各自的电机驱动,保持强制的联动关系,在滑动和滚动的共同作用下,磨粒切入和切出齿轮工件齿面,达到材料去除的目的。珩削力的切向力是由工件齿轮与珩磨轮展成运动引起的,其动力来源主要为工件齿轮轴的旋转,法向磨削力主要是由工件受到的径向力引起的,同时由于珩磨轮与工件属于交错轴斜齿轮传动,会产生轴向力。
珩削受力分解如图2所示。将珩削力集中到一点上,把珩削力按照上述分析依次分解为径向力Fr、圆周力Fs、轴向力Fa。
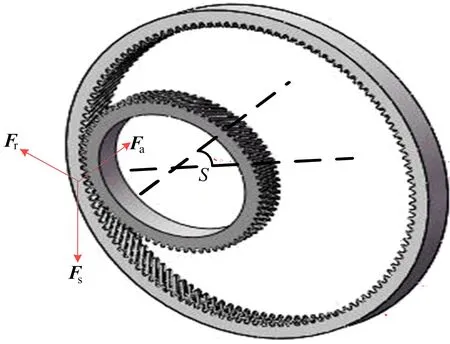
图2 珩削受力分解
Fr、Fs、Fa之间的关系如下:
(1)
其中:β为工件齿轮的螺旋角;αn为分度圆处的法向压力角。由(1)式可以看出,Fa和Fs主要与工件齿轮的螺旋角和分度圆处的法向压力角有关。
珩削力的径向分力Fr表示磨粒珩削深浅的程度,是影响珩削力大小的主要因素,因此主要对珩削的径向力Fr进行预测研究。而珩削本质上是低速磨削,试验设计因子选取为磨削三要素[10]。背吃刀量主要与珩轮径向进给量fx有关;进给量主要与珩轮轴向进给速度fz有关;切削速度主要与主轴转速C2有关。因此本次试验的设计因子选取为主轴转速C2、珩轮径向进给量fx、珩轮轴向进给速度fz。
2 珩削试验
2.1 试验材料及试验设备
试验加工的珩磨轮材料为微晶刚玉结合剂砂轮,被加工工件为20CrMnTiH。工件与珩轮材料的主要性能参数见表2所列。

表2 被珩工件与珩轮材料参数
试验采用的机床为生产应用最广泛的Fassler HMX-400强力珩齿机,如图3所示。

图3 Fassler HMX-400内齿强力珩齿机
2.2 试验设计
根据Fassler HMX-400珩齿机手册,主轴转速C2、珩轮径向进给量fx、珩轮轴向进给速度fz分别在800~1 800 r/min、2~8 μm/行程、60~200 mm/min范围之内。
采用正交试验方案L25(53),共计25组试验,正交试验表见表3所列。
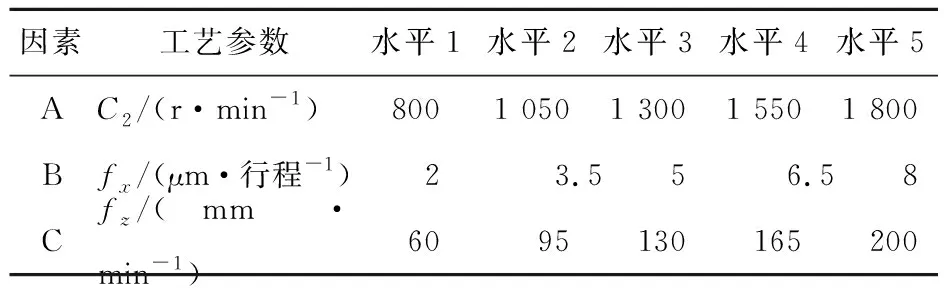
表3 工艺参数及其水平
部分试验设计点如图4所示,试验方案及结果见表4所列。

图4 部分试验设计点
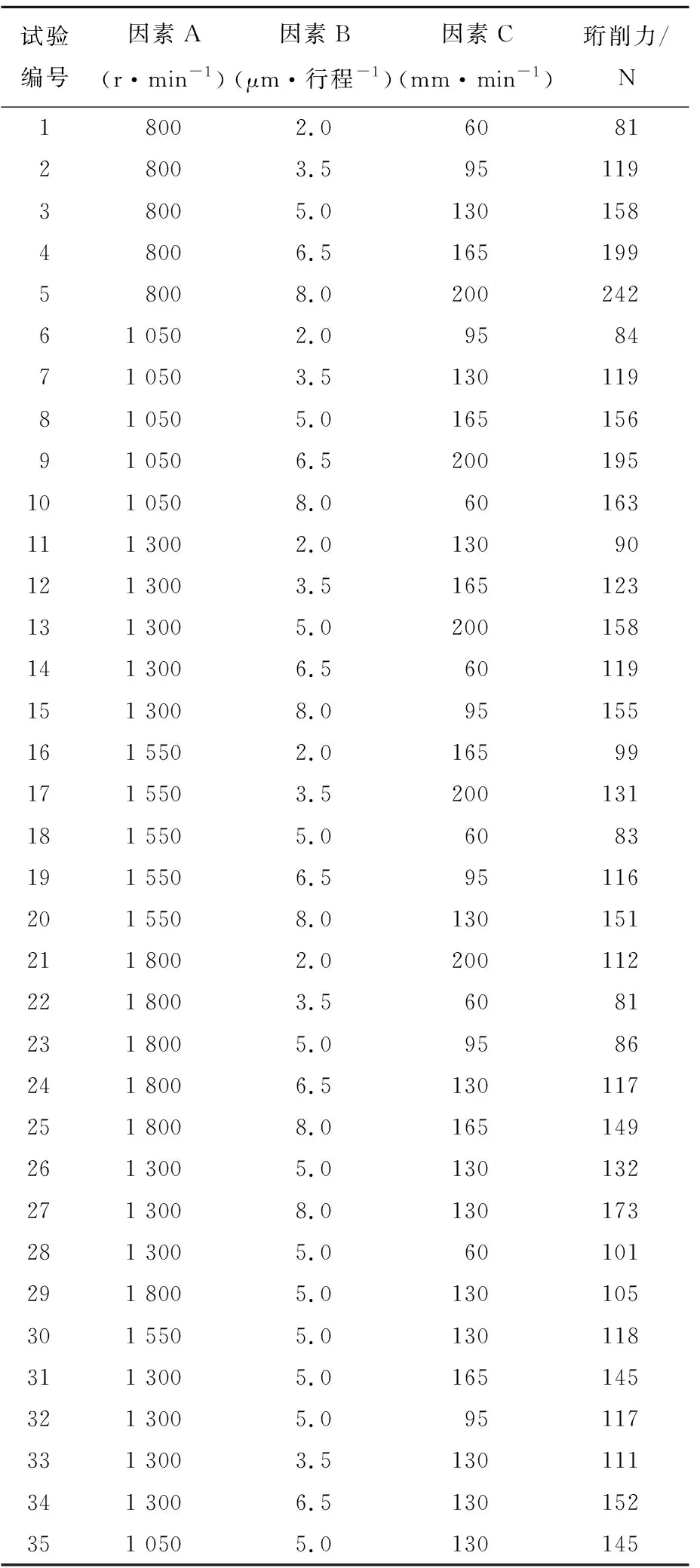
表4 试验方案及结果
由正交试验的特性可知,本文所提出的正交试验L25(53)的样本点基本分布于设计空间的外部表面,设计空间内部试验点仅有4个(图4),内部样本点不足会使神经网络在设计空间内部的预测准确度不足。因此,在现有正交试验的基础上,进一步开展单因素试验。
以(C2,fx,fz)=(1 300,5,130)为对称中心均匀增加设计空间的内部样本点(图4),去掉重叠的试验点,共进行了35组试验。在加工试验中珩削径向力由珩齿机主轴内部Kistler测力仪获得。
3 预测模型建立及分析
根据珩削加工试验获得的前30组数据,依次建立珩削力BP神经网络预测模型和指数型预测模型;利用后5组试验数据来判定2种预测模型的准确度。
3.1 BP神经网络预测模型
误差逆向传播算法的多层前馈神经网络,即典型的BP神经网络,由输入层、隐含层和输出层构成。每层的神经元数目不确定,需根据实际情况自行设置。同层的神经网络之间互不干扰,相邻层通过权值连接。输入的训练样本由输入层到达隐含层,通过一定算法对样本进行训练,最终通过输出层输出训练结果。
根据已开展的珩削试验,选定输入层神经元数目为3,隐含层层数神经元数目由经验公式选定为10,输出层神经元数目为1,训练的BP神经网络的结构如图5所示。
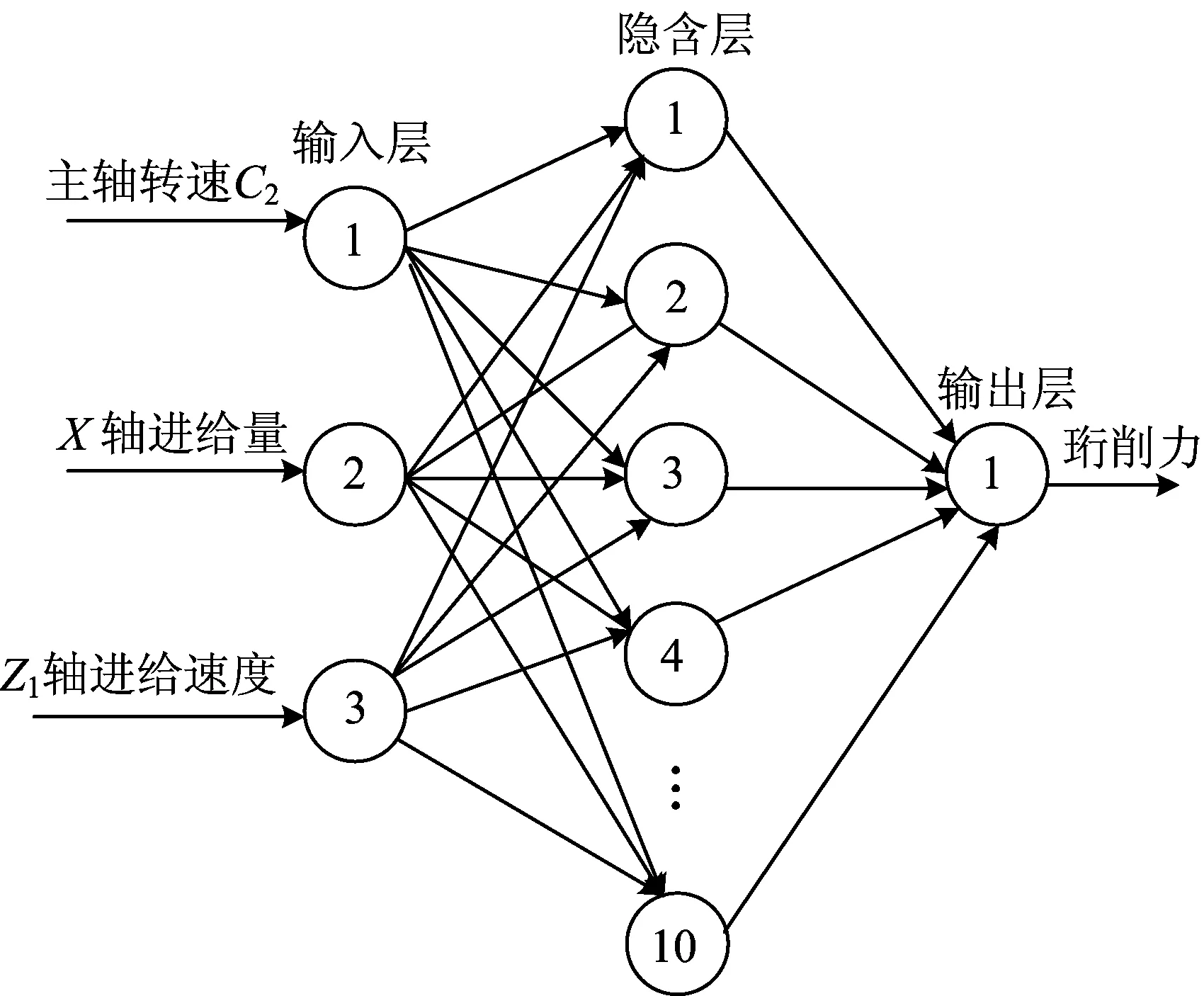
图5 珩削力预测BP神经网络结构
为防止样本输入、输出的数量级相差较大而造成后续网络训练预测差异大,采用Matlab R2016a中的mapminmax函数对其进行归一化处理,使得输入的样本都落在区间[0,1]上,其mapminmax函数关系为:
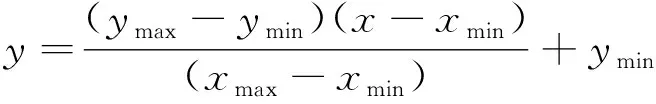
(2)
其中:ymin=0;ymax=1。
本文采用Matlab R2016a编写的BP神经网络训练[11],通过动量梯度下降法对所提出的神经网络进行训练。训练目标的最小误差为0.001,最大训练步长为2 000步。当训练误差小于训练目标的最小误差时,训练结束,形成内啮合强力珩齿珩削力的BP神经网络预测模型。网络误差变化曲线如图6所示。
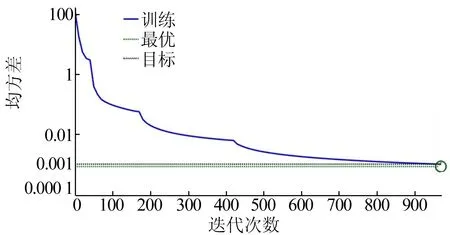
图6 网络误差变化曲线
为了检验编写的BP神经网络的可靠性,用决定系数的算术平方根R来量化神经网络的预测准度,即
(3)

训练样本、测试样本以及整体的R值如图7所示。
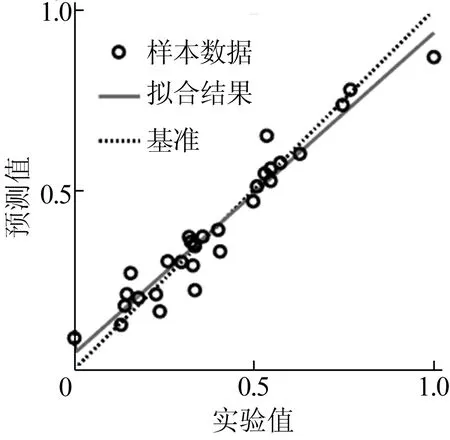
3.2 指数型预测公式
珩削本质属于低速磨削。假定珩削力与工艺参数满足指数型关系,为与指数型磨削力公式相区别,在公式后加一常量F0,则珩削力指数型预测公式为:
(4)
其中:F为珩削力;C2、fx、fz为主轴转速、X轴进给量、Z1轴进给速度;k为材料属性以及珩齿机本身对珩削力的影响;m、n、p为待定系数,其大小代表各要素对珩削力的影响程度。
对(4)式求对数,则有:
lg(F-F0)=lgk+mlgC2+nlgfx+plgfz
(5)
因为前30组数据中,试验得到的珩削力最小值81 N,为保证(4)式中lg(F-F0)有实际数学意义,即F-F0>0,所以取F0为80。采用MINITAB17软件进行多元线性回归,获得珩削力的指数型经验公式为:
(6)
由(6)式可看出,待定系数n>p>m,即珩轮径向进给量fx对珩削力的影响最显著,起主导作用,珩轮轴向进给速度fz次之,主轴转速C2影响程度最小。
3.3 预测结果及讨论
基于上述试验数据,建立内啮合强力珩齿珩削力BP神经网络预测模型和指数型预测模型。为了分析各模型的预测精度,用试验的后5组对其检验预测精度。将验证试验的珩削参数分别代入神经网络预测模型和指数型预测模型,得出不同珩削参数下的珩削力预测值,见表5所列。

表5 不同模型预测值及相对误差大小
由表5可知,BP神经网络的预测精度最高,误差基本都在5%以内,指数型公式的每组预测精度都比BP神经网络的预测精度低,最高的误差能达到18.94%,且误差的波动较大。试验值与2种预测模型的对比分析柱状图如图8所示。从图8可以更直观地看出,BP神经网络预测模型与珩削试验值拟合效果更好。虽然BP神经网络的预测效果要明显优于指数型模型预测效果,但是从使用方便性上指数型模型只需将各个参数数值直接代入公式即可得出珩削力数值大小,无需像BP神经网络进行复杂的训练。
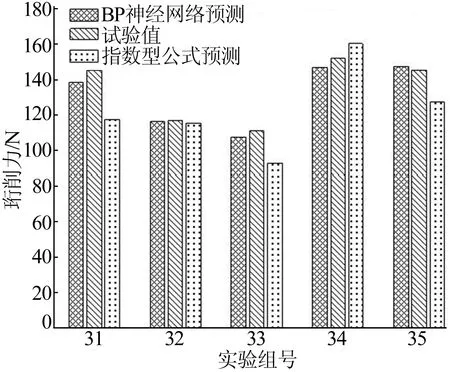
图8 模型预测值与试验值结果对比
因此,在准确度上BP神经网络模型要优于指数型预测模型,而在模型使用简便性上指数型模型则要优于BP神经网络预测模型。
4 结 论
(1) 本文根据内齿强力珩齿加工特性,选定了预测模型的输入量和输出量。试验所采取的方案为正交试验加单因素试验结合的设计方法,该方案与一般的正交试验方案相比,试验样本点能均匀分布于设计空间的内部与表面,具有准确性高的特点,避免了试验数据不具有概括性的缺陷。
(2) 在预测精度上,基于BP神经网络预测模型的预测相对误差显著小于指数型模型的预测值相对误差,基于BP神经网络预测模型的预测值相对误差均在5%以内;在模型使用简便性上,指数型模型比BP神经网络具有更高的可操作性。2种模型对内啮合强力珩齿珩削力的研究具有一定的参考价值,可根据现实需要灵活地选用预测方法。
