商用车驾驶室半主动悬置系统的研究与优化

张艺腾, 钟绍华, 桂 航, 关 挺

(武汉理工大学 汽车工程学院,湖北 武汉 430070)

半主动悬置系统的设计与优化通常分为2个方面:① 通过改进控制策略达到优化控制效果的目的[1-2];② 通过使用智能算法对控制系统的参数进行优化[5-6]。采用第1种优化方式的有:文献[3]开发的基于最优控制算法的驾驶室悬置系统;文献[4]设计的变论域模糊控制器。关于第2种优化方式的研究有很多。文献[7]通过遗传算法对悬置系统进行了改进和优化,拟合了空气弹簧和阻尼特性曲线;文献[8-9]基于悬置简化理论模型,通过遗传算法分别对模糊控制器和PID控制器参数进行了优化;文献[10]针对驾驶室全浮式空气弹簧悬置进行了建模优化。

当前对悬置系统的研究主要集中在以简化的理论模型为研究对象,通过遗传算法等对相关参数进行优化。而简化后的理论模型会失去悬置系统的部分特性,包括零部件间的干涉以及弹性元件的影响,同时优化中使用的算法在高维、非线性、多峰等特征问题上具有缺陷。

为解决上述问题,本文针对某商用车的实际结构,隔离出其悬置系统,通过ADAMS软件建立其多体动力学模型,并以实车平顺性试验数据对模型进行验证;通过Matlab/Simulink软件搭建模糊自适应比例积分微分(proportional integral differential,PID)控制系统模型,用以提供主动阻尼力,通过联合仿真将被动悬置系统改进为半主动悬置系统;以驾驶室地板处垂向加速度、驾驶室质心处垂向加速度和俯仰角加速度为监测对象,对仿真结果进行对比分析;基于联合仿真模型,以模糊PID控制器的隶属函数为优化对象,以偏差的时间乘绝对误差(integral time absolute error,ITAE)积分值和地板处垂向加速度、质心处俯仰角加速度均方根值为优化目标,通过差分进化(differential evolution,DE)算法进行多目标优化;最后对优化结果进行仿真和试验验证。

1 多体动力学模型搭建与验证

1.1 结构分析

将实际驾驶室悬置系统从整车中隔离出来,其三维模型如图1所示。

图1 悬置系统结构

该悬置下端与车架固连,上端与驾驶室固连。路面激励经过底盘主悬架系统衰减后传递至车架,再由车架传递至悬置系统作为系统输入激励,激励经悬置系统衰减后传递至驾驶室。使用隔离出来的悬置系统作为研究对象可以直接使用车架振动激励作为系统的输入信号,在整车参数不足的情况下提高研究的准确性。

悬置系统中除了4个空气弹簧和阻尼器外,还有横向稳定杆、横向减振器以及很多橡胶元件,这些零部件对于系统的影响不能忽略。该悬置系统的前悬结构为“剪刀式”结构,其空气弹簧支撑点与悬置下支点不同轴,在计算弹簧预载荷以及受力分析时需根据结构计算;后悬结构可简化为平面结构。

当驾驶室悬置系统在纵轴线方向对称且左、右两侧减振器输入相同时,可将其简化为平面运动模型;同时假设在垂直方向上前、后悬的振动互不干涉,则可以进一步简化模型变为单质量振动系统。因为实际的悬置系统前、后悬输入不一定相同,所以驾驶室在实际运动中可能出现俯仰或侧倾,需考虑双质量振动系统。双质量振动系统的简化力学模型如图2所示。

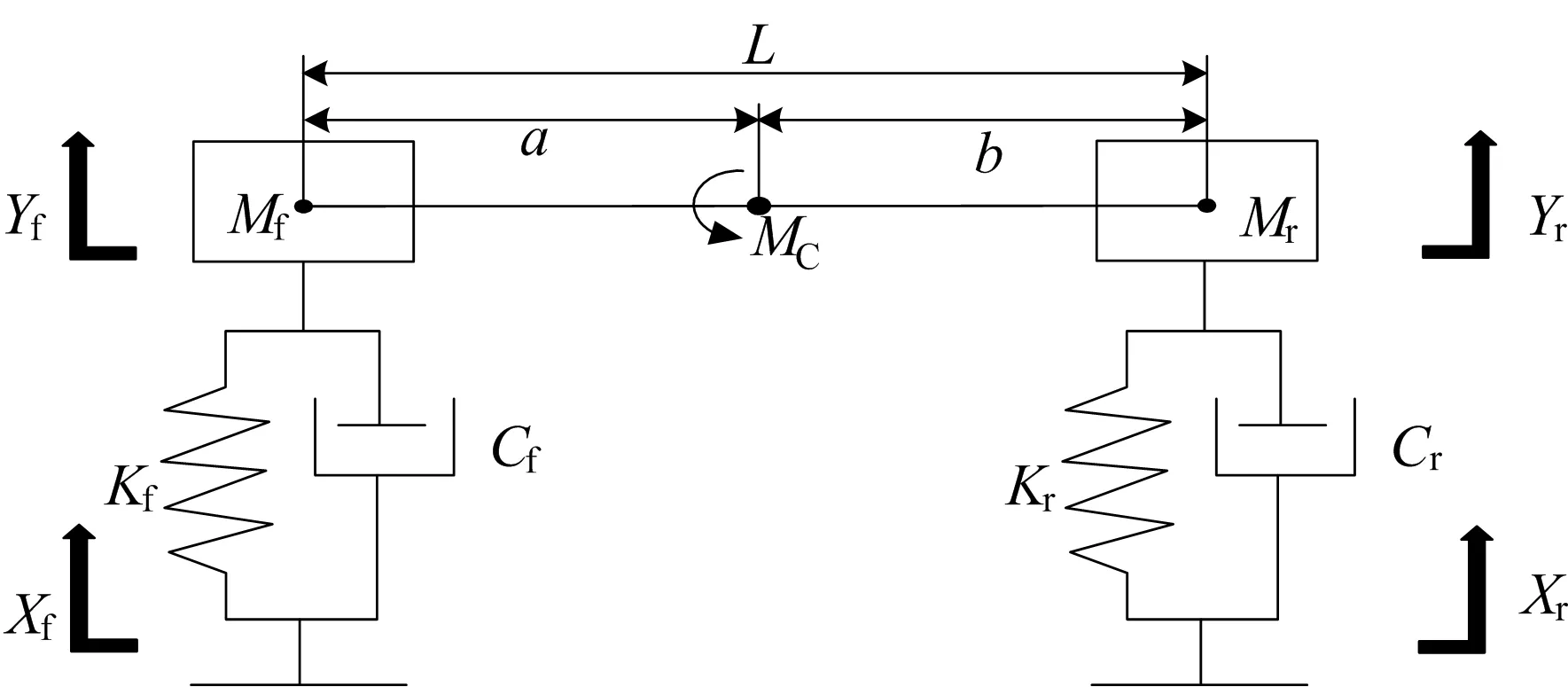
图2 双质量系统简化力学模型

类比单质量振动系统,可以求得系统垂向运动、俯仰运动的固有频率ωy和ωφ、2个运动方向的主频率ω1,2和主振型A1,2,即

(1)

(2)

(3)

(4)

其中:Kf、Kr分别为前、后悬的等效刚度;a、b分别为前、后悬距质心的距离;M、ρc分别为驾驶室惯性参数。由上式可知,当μ1=0时,垂直运动和俯仰运动的主频率互不干涉,此时可简化为单质量振动系统;当上述情况不成立时,需要考虑到俯仰运动对驾驶舒适性的影响,又因为俯仰运动会产生水平运动分量而恶化驾驶舒适性,所以减小俯仰运动十分重要。

1.2 模型搭建与验证

因为多自由度动力学模型求解较为麻烦,所以借用求解器求解。采用ADAMS软件建立驾驶室悬置系统的模型,并进行模型验证。本次建模中,相对位置的坐标系原点O选在驾驶室前围的中心孔;+X、+Y、+Z分别指向驾驶室后方、驾驶员右方和垂直地面向上。驾驶室的质量与弹性元件的部分参数见表1所列,其中驾驶室惯性参数通过质量线法测得[11]。

表1 悬置系统部分关键点参数

建模之前,为了在不影响模型精度的情况下降低建模难度,需要对驾驶室悬置系统做出如下假设:① 除弹簧、减振器、橡胶元件、横向稳定杆等弹性元件,其他结构均以刚性结构处理,包括驾驶室和乘员;② 横向稳定杆采用ADAMS内置模块进行柔性化处理,橡胶元件用bushing结构代替;③ 弹簧和减振器的刚度和阻尼特性简化为线性特性。

根据图1建立的驾驶室悬置系统ADAMS模型如图3所示。

图3 悬置系统的ADAMS模型

振动仿真之前,模型需要通过约束检查和静平衡验证,检验均顺利通过。该模型有63个自由度,除去地面有28个可移动部件。振动仿真的输入、输出位置均与试验中传感器位置相同。悬置下端以试验采集的车架衰减后的振动激励作为输入,将振动仿真的输出信号与试验采集的输出信号进行对比。

以车速为60 km/h时驾驶室脚部地板处功率谱密度(power spectral density,PSD)曲线为例,得到的振动仿真结果如图4所示。从图4可以看出,曲线值在20 Hz之后基本为0,因此截取0～20 Hz部分的曲线进行具体分析。

图4 60 km/h时PSD曲线仿真结果与试验结果的对比

各速度下PSD曲线峰值以及计算得到的加速度均方根值的对比见表2所列。

表2 驾驶室地板处仿真与试验的PSD峰值对比

从PSD曲线和表2可以看出:各速度下仿真得到的PSD曲线与试验数据转换成的曲线具有相同的趋势,对应峰值的横坐标相同,且峰值基本相同,峰值误差在5%左右;各速度下仿真和试验得到的驾驶室地板处垂向加速度均方根值的大小也基本相同,误差在5%左右。仿真精度满足工程的一般要求,可以认为该模型与实际悬置结构具有相同的特性,即共振峰位置、峰值以及加速度均方根值均基本相同,可以用该模型代替实际系统进行联合仿真。

1.3 导出模型

在联合仿真中,将阻尼力分为2个部分:① 减振器提供的定阻尼力,由ADAMS模型模拟;② 由控制系统输入给作动器的主动阻尼力。模型的输入采用ADAMS模型内部输入,因为要研究悬置系统的特性,同时联合仿真要在时域进行,所以内部输入采取时域正弦扫频输入。

前悬左侧采用1～10 Hz、幅值20 mm、时长20 s的正弦扫频输入,信号如图5所示;前悬右侧采用1 Hz、幅值20 mm、时长20 s的正弦输入;后悬输入与前悬输入相同但存在1 s的延迟。以驾驶室地板处的垂向加速度、驾驶室质心处的垂向加速度和俯仰角加速度为输出,设置完成后导出为Matlab格式文件。

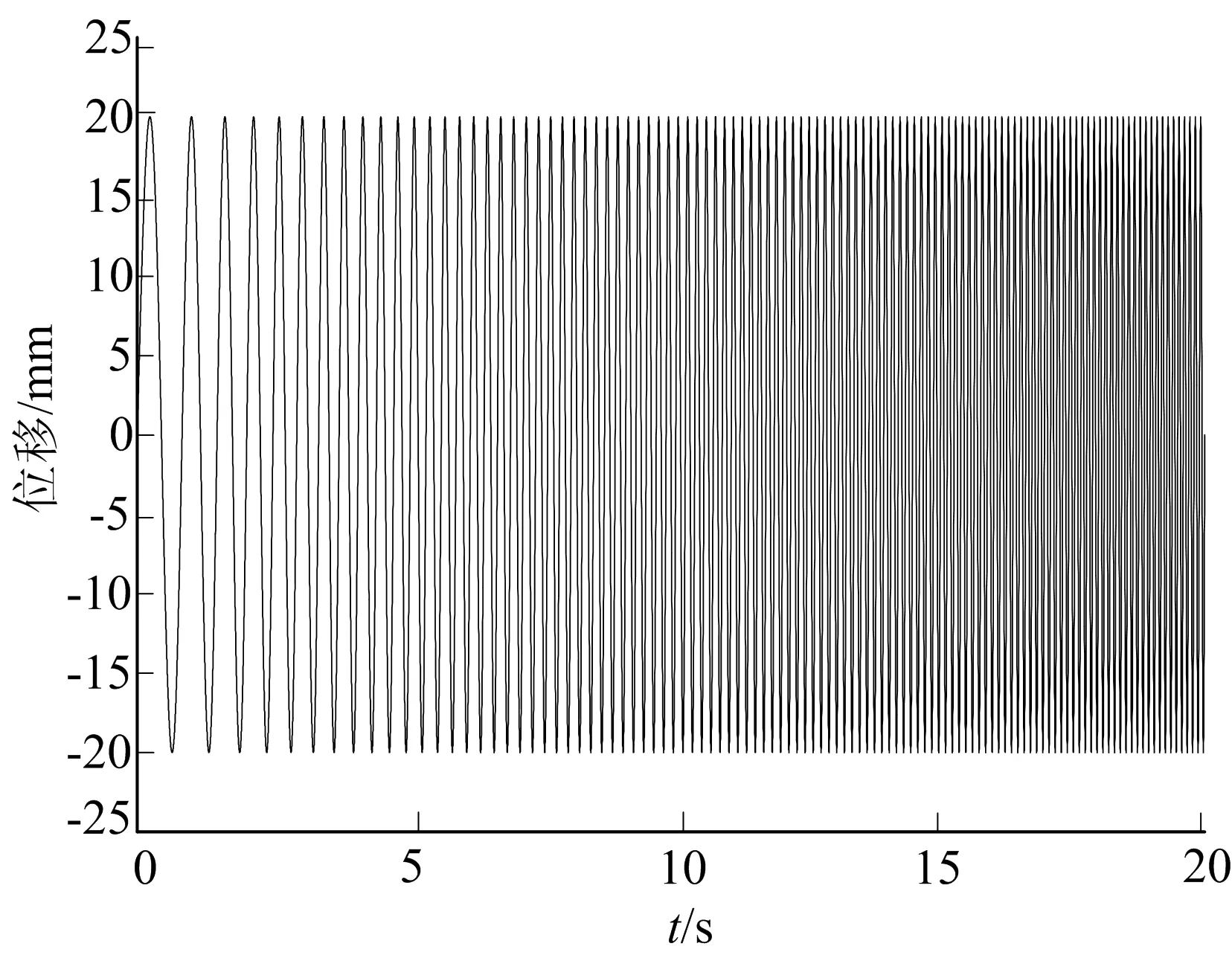
图5 输入扫频信号

2 控制系统模型

2.1 PID控制器

PID控制器是一种结构简单、参数明确、鲁棒性优秀、耐用性好的线性控制器,它可以通过对比理论值与实际值的偏差情况来计算最优控制力,从而减小偏差,增强系统的稳定性。其控制原理可以表示为:

(5)

采用衰减曲线法[12]整定参数,结果见表3所列。其中:kp为比例系数;ki为积分系数;kd为微分系数。

表3 PID参数

2.2 模糊自适应PID控制器

模糊控制器作为智能控制器有许多优点。为了弥补PID控制器参数无法更改的局限性,采用模糊控制对PID参数进行实时整定,设计模糊自适应PID控制器,以获得更好的控制效果。模糊自适应PID控制器工作原理如图6所示。

图6 模糊自适应PID控制器的工作原理

(6)

Kp=kp+Δkp=fp(e,ec)

(7)

Ki=ki+Δki=fi(e,ec)

(8)

Kd=kd+Δkd=fd(e,ec)

(9)

其中:Kp、Ki、Kd为经模糊控制器调节后PID控制器的3个参数;kp、ki、kd为PID控制器的原始参数;fp、fi、fd表示输入与输出的映射关系。

选取每个减振器上端输出的垂向速度与加速度误差e和误差变化率ec以及经过模糊计算后的输出Δkp、Δki、Δkd,设计一款双输入三输出的模糊自适应PID控制器。其中:误差和3个输出的论域为[-6,6];误差变化率的论域为[-36,36]。隶属度函数采用高斯型,模糊子集用{NB(负大),NM(负中),NS(负小),O(零),PS(正小),PM(正中),PB(正大)}语言变量表示。

模糊控制规则由专家经验和实际情况确定。在本次设计中,当控制器输入的速度较大时,无论加速度大小如何,均应输出反向较大的力使速度有减小的趋势;当速度较小但加速度较大时,输出较大的力抑制加速度;当速度较小且加速度较小时,应输出较小但与加速度方向相反的力,使速度稳定在较小值附近。以此类推,根据上述原则设计3个输出的控制规则。以Δkp控制规则为例,其模糊控制规则见表4所列。

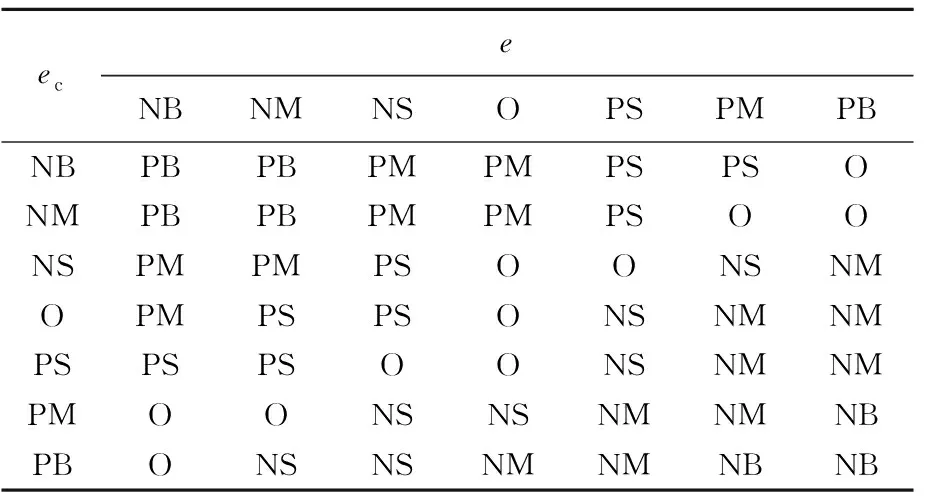
表4 Δkp控制规则

隶属函数表达式为:

(10)

解模糊化使用重心法,表达式为:

(11)

其中:μA(x)为输入变量x对应的隶属度;z为解模糊化后的输出。

由于4个悬置输出范围的不同,根据被动悬置仿真结果分别对4个控制器的相关参数进行设计,设计完成的模糊自适应PID控制器控制的半主动悬置系统如图7所示。

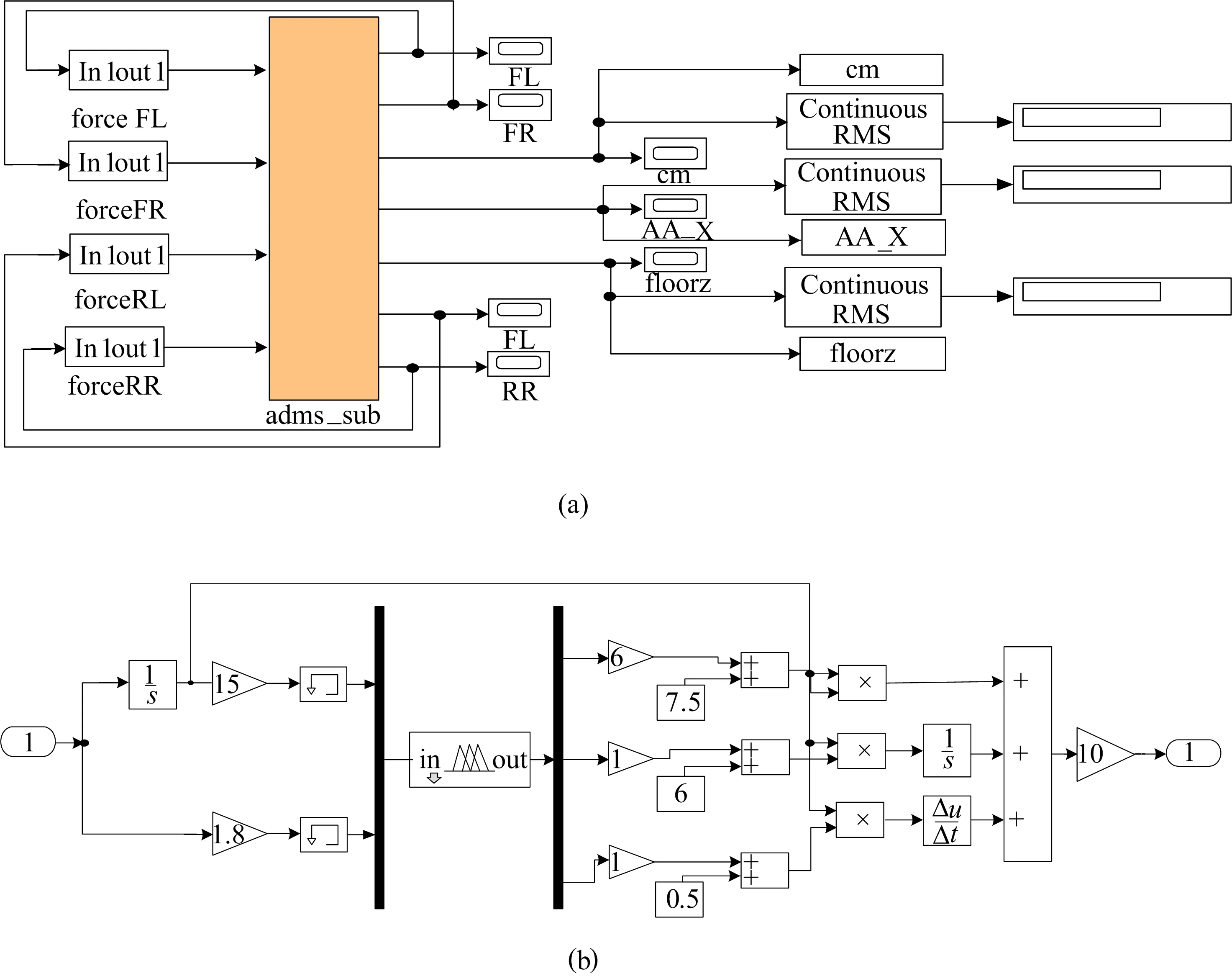
图7 半主动悬置系统模型

3 联合仿真结果分析

对联合仿真结果进行处理,得到在被动悬置、使用PID控制器和使用模糊PID控制器的半主动悬置系统下驾驶室地板处垂向加速度以及驾驶室质心处垂向加速度、俯仰角加速度随时间的变化曲线,如图8所示。

图8中:1表示被动悬置系统;2表示使用PID控制器的半主动悬置系统;3表示使用模糊PID控制器的半主动悬置系统。

由图8可知,输出的振动波形与输入信号的波形相关,驾驶室地板处的振动更接近靠近采集点一侧的减振器振动规律,驾驶室质心处的振动是整个系统共同作用的结果,这2处的振动加速度都能在一定程度上反应驾驶室的振动情况。因为系统输入是扫频与正弦信号,所以系统输入的速度和加速度不断增大,输出的加速度也呈上升趋势。与被动悬置系统相比,半主动悬置系统对驾驶室的垂向加速度和俯仰角加速度有一定的优化,但PID控制器与模糊PID控制器控制效果不同。从3个采集点的加速度可以看出:当输入激励较小即低速段时,PID控制的优化效果不明显;当速度逐渐上升,输入激励变化较快时,PID逐渐表现出较好的优化效果;模糊PID控制在整个速度段均有十分显著的优化效果,对垂向加速度和俯仰角角速度均有较大的抑制,优于被动悬置系统和PID控制器的悬置系统。

图8 联合仿真结果

计算得到的加速度均方根值见表5所列。

表5 联合仿真结果对比

4 半主动悬置系统多目标优化

当前对于悬置系统控制器参数的优化中存在如下问题:① 使用的控制对象多为系统的传递函数或简化后的理论模型,导致优化结果与实际需求相差甚远,缺少参考和应用价值;② 使用的优化算法在此类问题中易陷入局部最优解且计算效率低下,对于性能优异的算法关注较少;③ 使用的目标函数较为单一,只考虑单一目标而忽略复杂系统有较多评价指标,导致优化效果有限。

为解决上述问题,本文提出一种基于联合仿真模型、采用DE算法对控制器参数进行多目标优化的优化策略。使用联合仿真模型,考虑了复杂系统中各部件间的干涉以及重要元件对系统的影响;DE算法在高维、非线性、多峰等特征问题上具有天然的优势[6],故选其作为优化算法;在多目标优化中考虑了控制器的响应特性以及控制效果,避免了只关注单一指标而忽略其他指标的问题,使整体优化效果更佳。

4.1 多目标优化问题的描述

针对模糊PID控制器的设计过于依赖经验这一问题,以优化隶属函数的参数为例,对模糊PID控制器进行多目标优化。以降低联合仿真模型输出的驾驶室地板处垂向加速度、质心处俯仰角加速度均方根值以及控制器输入偏差的ITAE积分值为优化目标,以隶属函数的参数为优化变量,对悬置系统进行多目标优化。半主动悬置系统使用的模糊PID控制器为双输入三输出,因此隶属函数共计5×7=35个。上文所述隶属函数为高斯型(见(10)式),每个隶属函数均有a、b2个参数待优化,由于硬件条件有限,令每个输入或输出信号对应的隶属函数的b参数相同,则待优化变量的数量为5×7+5=40个。用x表示待优化变量,写成矩阵形式为:

(12)

其中:xi1(i=1,2,3,4,5)对应e、ec、Kp、Ki、Kd中隶属函数的b参数;xi2～xi8(i=1,2,3,4,5)表示对应模糊变量隶属函数的a参数。

目标函数为联合模型输出的驾驶室地板处垂向加速度和质心处俯仰角加速度的均方根值f1(x)、f2(x)以及表示4个控制器响应特性的ITAE积分值平均值f3(x)。因为待优化参数较多,且半主动悬置系统较为复杂,导致无法写出相关加速度均方根值的数学表达式,所以通过联合仿真模型对评价函数进行计算。f3(x)的表达式如下:

(13)

其中:i=1,2,3,4与4个悬置对应;ei(t)为偏差。

为了将多目标优化问题转化为单目标优化问题,使用线性加权法[13]对多目标问题进行处理,得到的评价函数J可以写为如下形式:

J=0.5f1(x)+0.4f2(x)+0.1f3(x)

(14)

4.2 DE算法优化

DE算法属于随机启发式搜索算法,利用达尔文进化规律,采用实数编码,通过变异、交叉、选择进行优胜劣汰,得到最优解。随机产生初始种群,选择种群中随机2个个体向量A、B的差向量D与第3个个体C加权求和,得到变异个体M,再通过M与C的交叉生成试验个体N,N与C比较适应度,选择较优个体作为下一代的个体元素。DE算法比遗传算法收敛速度快,比粒子群算法稳定且容易跳出局部最优解。优化流程如图9所示。

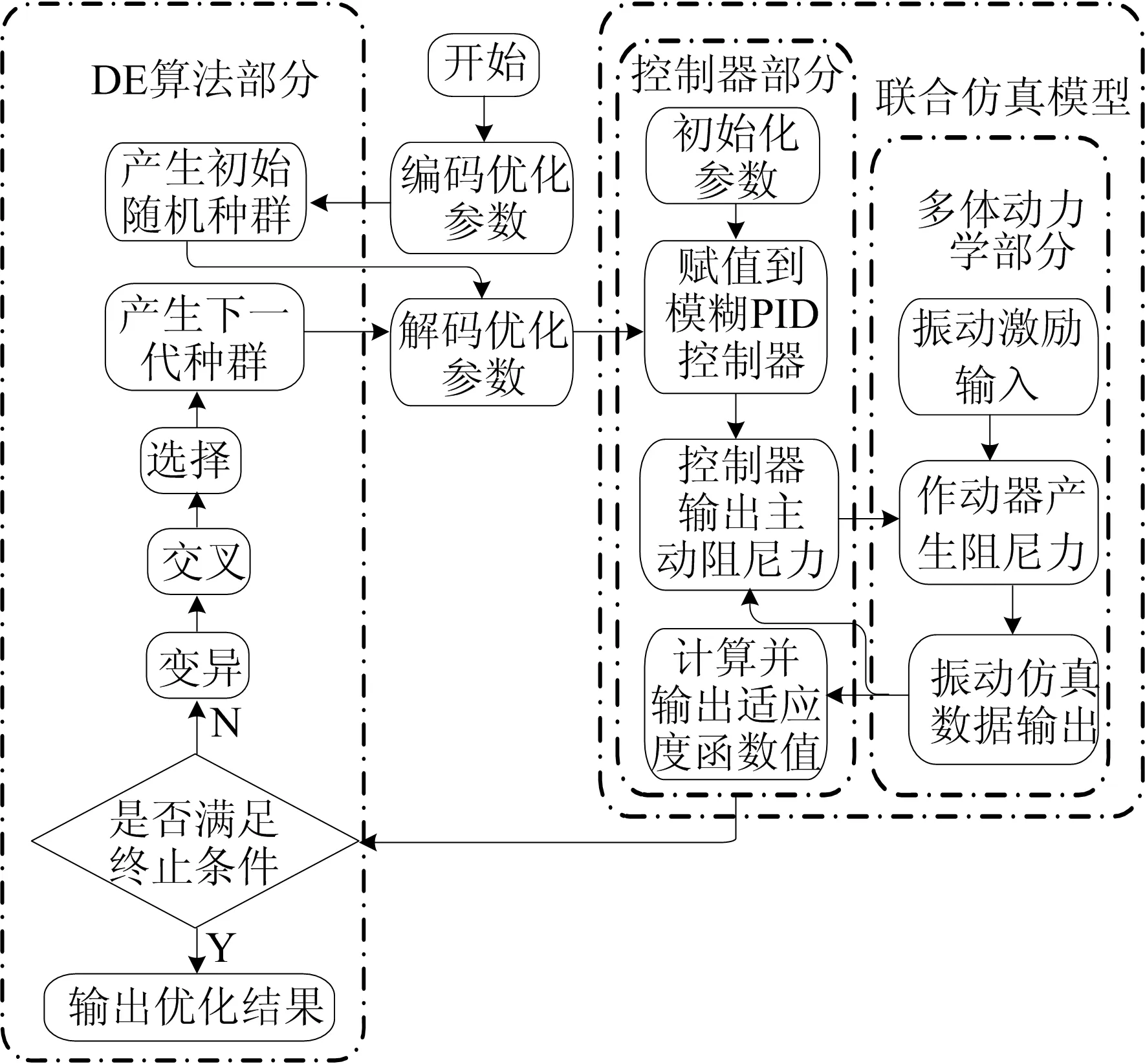
图9 优化流程

设置种群规模为160个,迭代次数为200,变异因子为0.95,交叉因子为0.6,以评价函数J为适应度函数。优化前、后适应度函数值由7.510 4降至6.297 3,优化效果达到16.15%。最低适应度函数值在115代后产生。优化效果受限是由于只对隶属函数进行优化,而没有优化模糊规则,得到的结果为在当前模糊规则下的最优隶属函数。

以偏差e的隶属函数为例,优化结果见表6所列。

表6 优化结果

4.3 优化结果验证

将优化结果导入上述半主动悬置系统中进行验证,并与优化前的模糊PID控制器控制效果进行对比。优化后驾驶室地板处垂向加速度、质心处垂向加速度、俯仰角加速度随时间的变化曲线如图10所示。图10中:1表示使用模糊PID控制器的半主动悬置系统;2表示DE算法优化后的模糊PID控制器半主动悬置系统。

图10 优化后联合仿真结果

优化后各项指标的对比结果见表7所列。

从图10和表7可以看出:驾驶室地板处垂向加速度、质心处垂向加速度和俯仰角加速度均方根值均降低10%左右,控制器控制效果明显提升,有效提升了驾驶舒适性;ITAE积分值平均值降低10%左右,控制器响应速度显著提升,降低了瞬态响应的振荡。

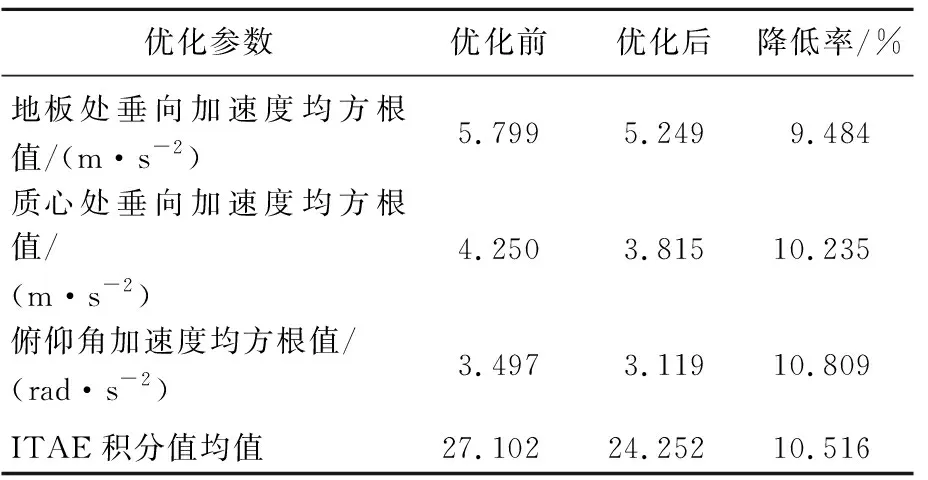
表7 各项优化指标对比

仿真对比结果表明本文优化方法可行,且优化效果明显,能得到具有最佳隶属函数的模糊PID控制器。

5 试验验证

在GB/T 4970—2009[14]中,规定了商用车行驶平顺性的试验方法。试验车辆由企业提供,本次试验采用2种悬置结构,即被动悬置和优化后的模糊PID控制的半主动悬置。被动悬置的试验数据还用于多体动力学模型的验证。

加速度传感器主要布置在4个悬置上下两端、驾驶员座椅坐垫、靠背以及脚步地板,其中前、后悬置上的加速度传感器为单向加速度传感器,驾驶室内的传感器为三向加速度传感器。具体布置位置如图11所示。

图11 试验观测点(部分)

本次试验所需的设备有LMS数据采集器与后处理软件、8个单向加速度传感器、3个三向加速度传感器以及线束若干,试验前对试验设备进行标定。

GB/T 4970—2009中对试验条件进行了规定:试验道路应是坡度不大于1%的平直沥青或水泥道路,道路上没有突变,且路面长度应该满足试验需求;试验场地风速需在5 m/s以内;汽车部件和传感器等装备完整,轮胎压力合适,载荷为最大装载质量。

本次试验中各条件均符合,试验车速在40～70 km/h之间,间隔10 km/h。

根据要求设置试验参数,使用1/3倍频程的导出数据计算得到总加权加速度均方根,在40、50、60、70 km/h时通过试验数据计算得到的总加权加速度均方根值，见表8所列。

以60 km/h为例,2种悬置试验数据的PSD曲线对比如图12所示,PSD曲线峰值对比见表9所列。

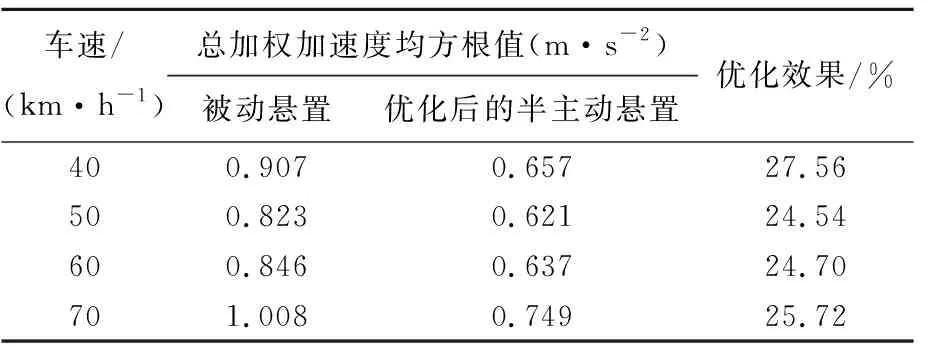
表8 各速度下总加权加速度均方根值

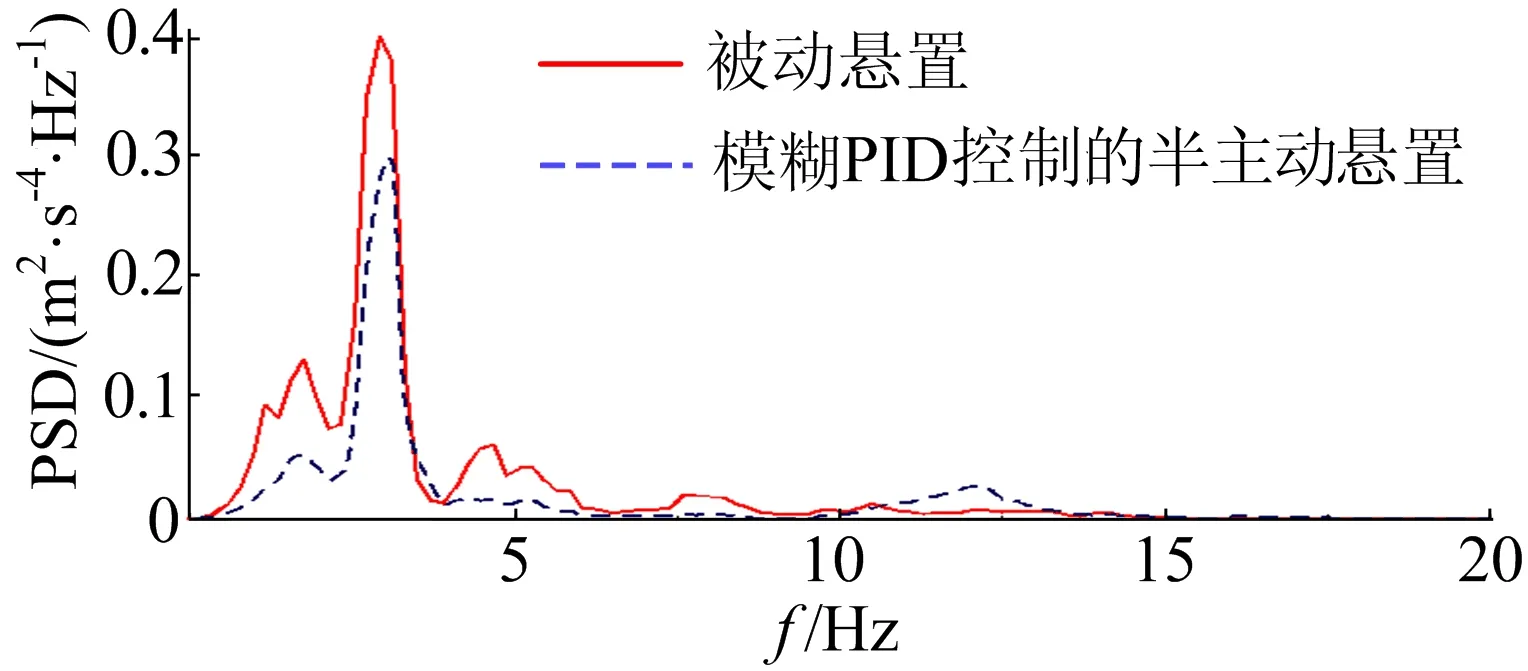
图12 60 km/h试验数据的对比

表9 试验中各速度下PSD曲线峰值对比

从表8、表9可以看出,优化后的半主动悬置相比于被动悬置有更好的平顺性,在40～70 km/h的速度段,总加权加速度均方根值下降25%左右,对应的PSD曲线的峰值降低25%左右。这表明优化后的半主动悬置系统对驾驶平顺性有十分显著的提升。

试验结果与仿真结果基本一致,但并没有仿真中优化效果明显,这是由于仿真模型对实际模型进行了一定程度的简化。

6 结 论

(1) 本文隔离出的实际悬置系统结构建立的ADAMS模型用试验数据校正后,能更准确地反应实际悬置结构的特性,用于联合仿真中更贴近实际情况,且考虑了各结构之间的干涉以及其他弹性元件对系统的影响,提高了开发效率,为之后的半主动悬置系统的开发提供了新的思路。

(2) 通过对比被动悬置系统、PID控制悬置系统、模糊自适应PID控制悬置系统的性能参数可以发现,半主动悬置系统比被动悬置系统有更好的平顺性,在垂向加速度和俯仰角加速度的优化方面效果明显,且模糊PID控制器的效果更优。PID控制器对被动悬置的优化效果达到22%左右,模糊PID控制器对被动悬置的优化效果达到35%左右。

(3) 基于联合仿真模型,以模糊PID控制器的隶属函数参数为待优化变量,以模型输出的驾驶室地板处垂向加速度和质心处俯仰角加速度均方根值与控制器输入的ITAE积分值作为优化目标,通过DE算法对其进行优化。经验证,该方法优化效果明显,优化率达到10%左右,证明了该优化方法可行。