利用手机传感器测定刚体的惯性张量
2021-11-06楼晨煊周婧琳郑雪瑶刘珂溦罗丹楠白在桥
楼晨煊,周婧琳,郑雪瑶,刘珂溦,罗丹楠,白在桥
(北京师范大学 物理学系,北京 100875)
在研究转动问题时,刚体的惯性张量是一个重要的参量. 在大学物理实验中,惯性张量的测量一般只限于刚体绕某固定轴的转动惯量. 对于质量分布情况未知的刚体,至少需要测量六个绕不同轴的转动惯量才可以得到完整的惯性张量[1].
目前利用手机传感器测定刚体某个方向上的转动惯量已是比较成熟的物理实验[2,3]. 事实上,手机陀螺仪传感器可以同时记录手机(作为一个刚体)3个方向的角速度变化曲线,可利用这个便利性研究刚体的三维转动. 本文讨论一种测量手机惯性张量(相对值)的测量方法. 这个方法只需要以不同初始角速度释放手机,利用phyphox软件记录手机在空中下落并自由转动过程中的角速度变化曲线,然后利用质心系中的转动动能守恒与总角动量守恒,就可以计算出手机惯性张量各矩阵元的相对大小. 这个方法的一大优点是:由于转动动能与总角动量都是标量,在数据处理中可以避开繁琐的坐标变换计算.
1 实验原理
1.1 简化惯性张量
刚体的惯性张量通常表示为以下的3×3对阵矩阵,
(1)
因为手机几何对称性好,质量分布大致均匀,不妨先仅假设M的非对角元素为零,即
(2)
这里为方便起见,已将Ixx、Iyy,、Izz分别简记为Ix、Iy、Iz.
在自由落体运动过程中,如果忽略空气阻力,手机在质心系中满足转动动能守恒与总角动量守恒[4]. 设phyphox软件在一次自由落体运动过程中记录到的角速度矢量为
(3)
其中k=1, 2, 3, … ,N为数据点编号. 质心系中的转动动能和总角动量的平方可以表示为
(4)
(5)
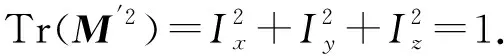
先考虑转动动能守恒.可把极小化的目标函数定为
(6)
容易证明,当该目标函数取极小值时,
(7)
这样目标函数可化简为
(Ix,Iy,Iz)A(Ix,Iy,Iz)T
(8)
其中
(9)
(10)
a=x、y、z.类似地,总角动量平方守恒对应的目标函数为
(11)

(12)

(αe11+βe21)2e31+(αe12+βe22)2e32+
(αe13+βe23)2e33=0
(13)

pγ2+2qγ+w=0
(14)
其中
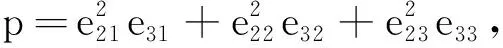
q=e11e21e31+e12e22e32+e13e23e33,
(15)
γ至多有两个实数解. 此外,由于三个转动惯量平方和为1,如果用到的3个特征向量已经归一化,则要求α2+β2=1. 考虑到Ix、Iy、Iz>0,上面的方程组至多有两个物理上合理的解,容易根据实际情况选择正确的解. 需要指出的是:由于矩阵A的形式并不依赖于转动动能与总角动量的大小,为了减小测量的随机误差,可以记录多次落体运动,先计算每条轨道测量的A,然后把结果相加,用所得矩阵进行后续的计算.
1.2 完整惯性张量
如果考虑惯性张量的非对角元,k时刻手机的转动动能和总角动量平方可以表示为
(16)
假设优化目标函数为
(17)
其中sE、sJ为权重系数,下面为简单起见,取sE=2,sJ=1/2.
类似前面的推导,先对E和J2求极值,目标函数可以表示为
(18)
其中
(19)

(20)
除了对称性MT=M,可要求M满足Tr(M2)=1. 注意现在可以把不同轨道的数据合并,得到更全面的目标函数,即每条轨道的数据独立计算出一个目标函数,再把所有结果相加.为简单起见,下面的公式略去了对不同轨道的求和.目标函数的梯度可以表示为
(21)
为使得Tr(M2)=1, 梯度方向应修正为
(22)
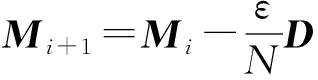
2 实验方法
2.1 坐标轴的确定
打开phyphox软件,将手机分别绕长宽高转动,监视陀螺仪角速度数据. 可以发现,当手机绕短边转动时,y轴有明显的数据变化,另外两个方向数据几乎为0,因此判断手机长边的方向对应y轴. 类似地可确定x轴和z轴,结果如图1所示.
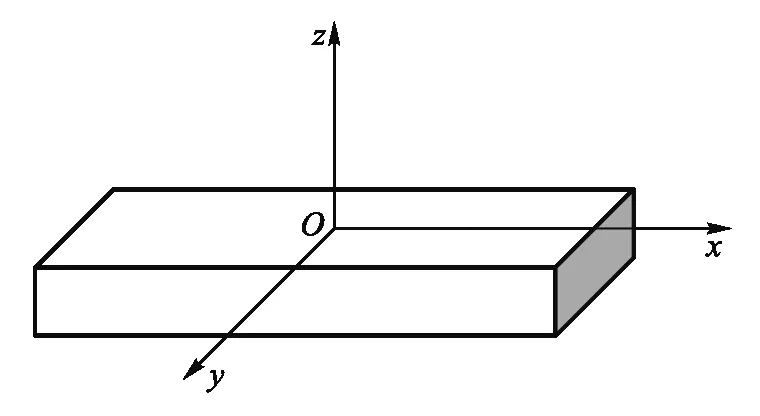
图1 phyphox与质心系坐标
2.2 角速度测量
打开phyphox软件中的陀螺仪模块,设置定时运行,0.5 s后开始测量. 运行后将手机从高处释放,使其自由下落到柔软的平面上. 为丰富测量数据,每次尽可能给手机一个不同的初始角速度. 最后截取出手机在空中自由转动过程中的数据用于后面的分析.
2.3 阻尼修正
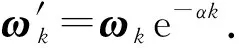

图2 修正前后的能量,角动量平方随时间变化图
3 实验结果
3.1 简化的惯性张量
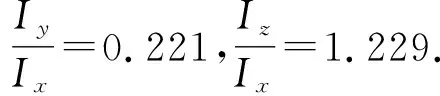
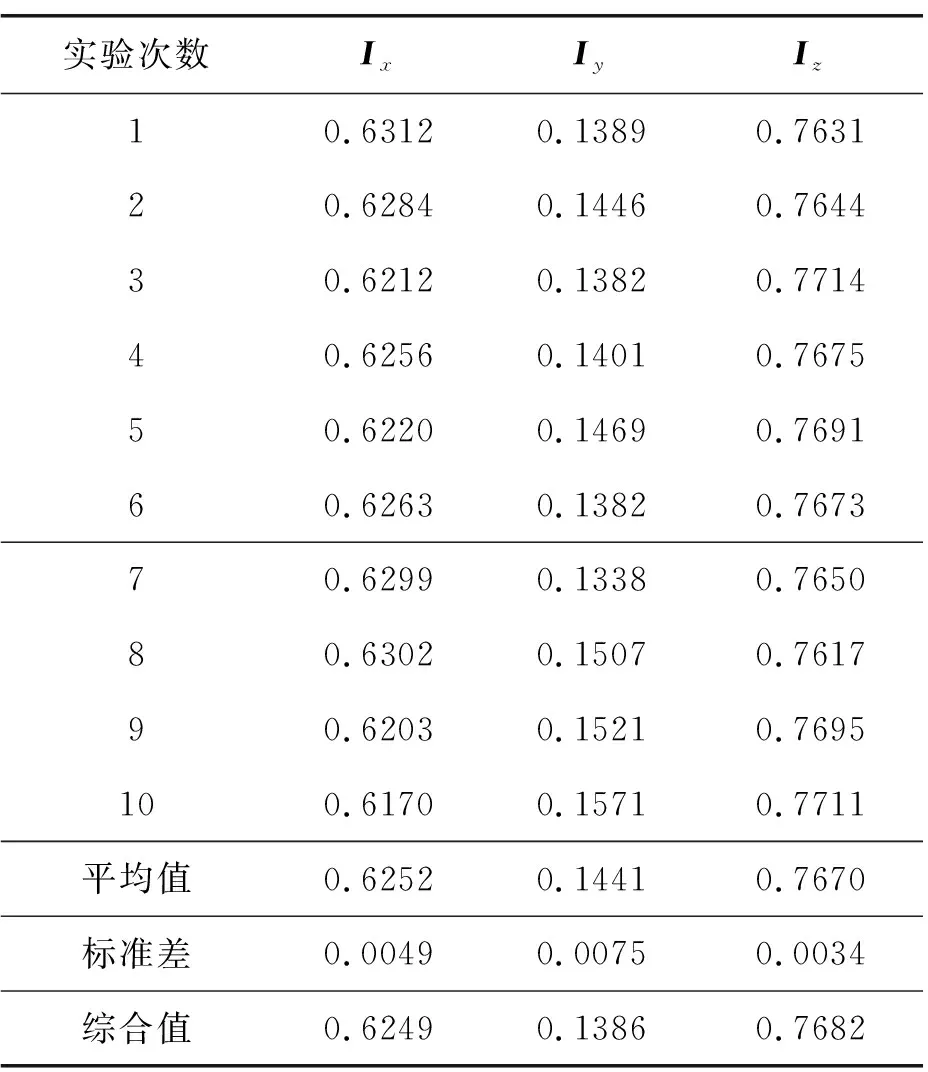
表1 惯量矩阵对角元素相对值
3.2 计算完整惯性张量
将记录的18条角速度曲线进行阻尼修正,按照2.2中的方法,在Matlab中编写程序进行计算.可以将上一步中计算得到的对角元作为初始值,以加快收敛.
18组数据得出的惯性张量结果为

为评估各个矩阵元的误差大小,将这18组数据分为三组,分别利用相同方法求解出相对惯量矩阵,结果如下.
基于这3次结果,估计各个矩阵元的不确定度,结果为

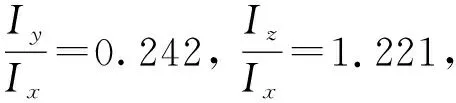
3.3 结果验证
为验证结果的准确性,可以将手机近似认为质量均匀分布的长方体刚体,根据测量得到的长度参数,计算三个对角元的相对值. 手机的长宽高分别为155.3 mm,75.0 mm,7.5 mm,根据
计算得到
结果均和前文测量结果吻合较好.
在上述测量、计算方法过程中,将角动量的平方作为一个守恒量. 事实上,角动量本身也是一个守恒量,而欧拉动力学则描述了这个过程:
(23)
注意角加速度只与惯性矩阵的相对大小有关. 将测量的惯性矩阵代入欧拉动力学方程的三个分量式中,计算出角加速度曲线. 同时,对测得的角速度-时间曲线,取相邻的5个点进行二次多项式拟合,求得中间点的斜率作为此时的角加速度,得到实测角加速度曲线. 图3和图4给出在两条轨道上得到的两种角加速度结果. 图中‘×’表示实测的角加速度值,实线为由欧拉方程计算得到的角加速度. 可以看到,两种方法计算得到的三个方向上的角加速度基本一致,这进一步验证了本文方法所得惯性张量的可靠性.

图3 角加速度-时间曲线1
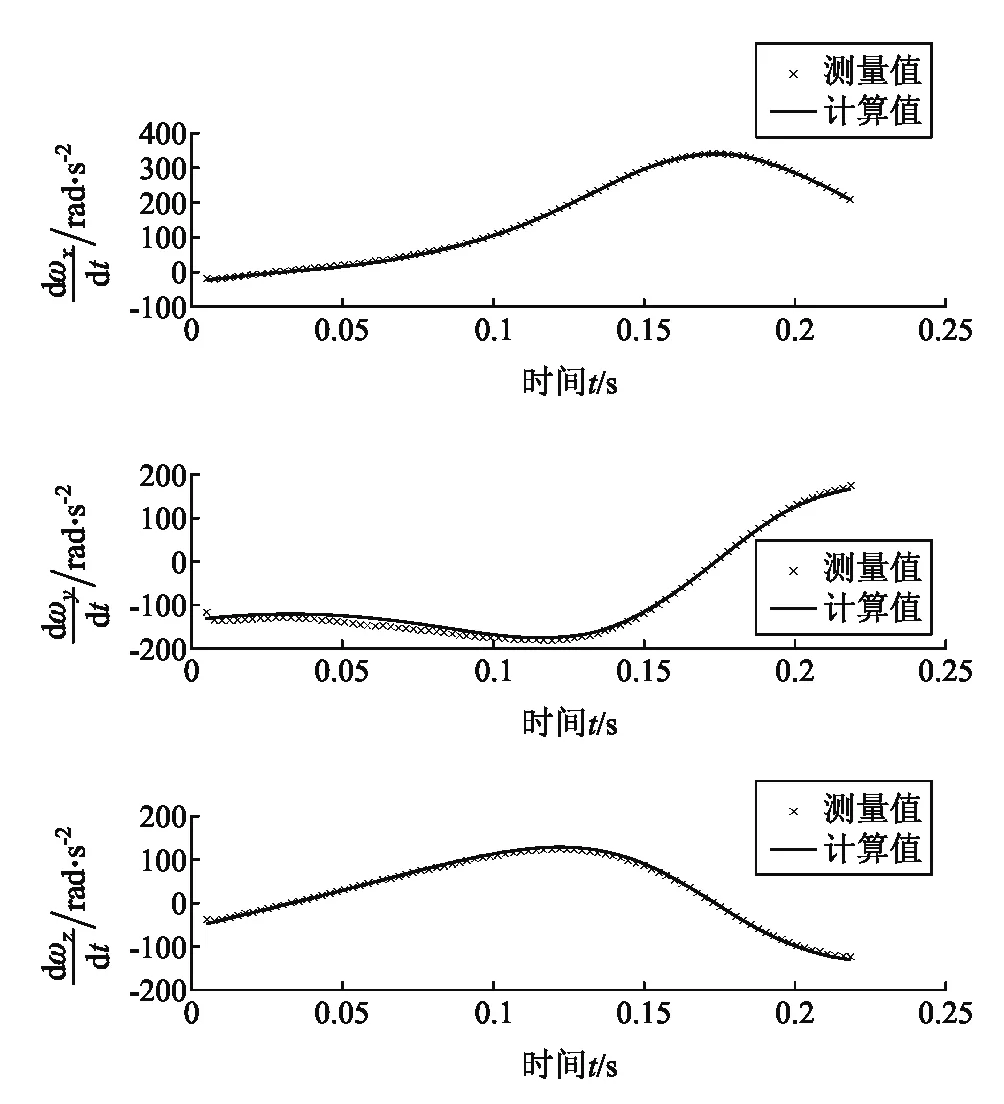
图4 角加速度-时间曲线2
4 总结
本文利用质心系中的转动动能守恒和角动量守恒,从一条或多条刚体自由下落轨道的角速度曲线计算了刚体的惯性矩阵. 目前利用了手机陀螺仪和phyphox软件测量了手机的惯性矩阵. 原则上,使用无线陀螺仪模块,也可以对其它刚体进行测量. 这种方法利用较多的刚体转动规律和数据处理方法,对刚体动力学和物理实验教学都有一定的参考意义.
