一维受迫谐振子的几何相位

孙玉明

(烟台大学物理系，山东 烟台 264005 )

受迫谐振子是一类可以解析求解的含时问题，求解方法大致上分为不变算符法[1-3]、幺正变换法[4]、李代数法[5]和格林函数法[6].根据系统特点选择合适的方法,一般可以得到系统的量子态. 因为哈密顿量含时,系统能量不守恒,量子态在希尔伯特空间中的运动轨迹更加复杂，路径的特点体现在量子态的几何相位中. 不少文献已经对含时谐振子的几何相位进行了讨论[6-8],不过对绝热近似下的Berry相位研究的多一些,对非绝热或非循环的情况涉及不多. 在以不变算符法和格林函数法为基础的研究中,则需要求解辅助微分方程或者参数微分方程，它们的求解往往很困难.本文结合幺正变换法和李代数法给出了1维受迫谐振子的1种简洁求解方法,而且讨论了量子态循环和非循环演化时的几何相位.

1 受迫谐振子的量子态

(1)

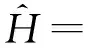
(2)

(3)

(4)

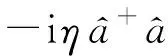
(5)

也构成1个李代数[9],对易关系是

[Mη,Mr]=Mr, [Mη,Ml]=-Ml,

[Ml,Mr]=Mδ, [Mη,Mδ]=0

(6)

-iηMη和-i(rMr+lMl+δMδ)分别是该空间中的矢量,它们在李群中的元素是指数矩阵e-iηMη和e-i(rMr+lMl+δMδ).

(7)

(8)

哈密顿算符式(2)的矩阵形式是

(9)

(10)

(11)

根据表4可以得知，中国绿色经济增长数值随着总产出的增加而增加。而在近10年的产出中，虚值比例是逐年下降的，与10年前的虚值比1.32%相比，近三年的虚值比均未超过0.7%。产生这种现象的原因是：虽然10年以来产出和煤炭消费都呈现增长的趋势，但是煤炭消费增长速度小于产出的增长速度，所以在此基础上计算出来的产出的虚值比在缓慢下降。同时，在某种程度上也表明了中国近年来所采取的向绿色、环保、低碳方向发展的政策起到了一定的作用，为了创造生产总值而付出的环境成本在不断降低。

(12)

(13)

(14)

(15)

(16)

只要再次应用李代数的特点，由式(8)与式(16)的矩阵表示相等,可得等式:

(17)

由此我们得到

(18)

(19)

假设系统的初始态是真空态|ψ(0)〉=|0〉:

e-iδ|z(t)〉

(20)

其中第3行应用了l和r互为复共轭的关系.第4行应用了指数算符分解形式:

(21)

式(20)的最后结果是一个相干态[10],z(t)=-il*e-iωt.

2 几何相位

在量子力学中|ψ〉和eiλ|ψ〉,只是相位不同.将一个量子系统[11]中只存在相位差别的态用希尔伯特空间中一条直线表示(如图1中的直线),用微分几何的语言,把它叫做纤维或者射线.量子系统从初态|ψ(0)〉开始依照薛定谔方程随时间演化,如果经过时间T后,量子态|ψ(T)〉与|ψ(0)〉处于同一条射线上,但相位不同,在希尔伯特空间中的轨迹是一条非闭合的曲线(如图1中上部的实线所示),那么称之为循环演化.如果起点和终点量子态在同一条射线上,而且相位相同,那么轨迹是一条闭合曲线(如图1中虚线所示),称之为周期性演化.假设一个量子系统量子态遵循薛定谔方程的演化轨迹是图1中的实线|ψ(t)〉,它在相空间P(H)中的投影是闭合曲线C.投影到C上的曲线有无穷条.希尔伯特空间中2条曲线在相空间中的投影相同,那么它们之间存在规范变换.假设图1中曲线|ψ(t)〉和|φ(t)〉在相空间P(H)中投影都是闭合曲线C,即量子态循环演化,它们之间规范变换关系是:|ψ(t)〉=eif(t)|φ(t)〉,f(0)=f(T).若将|ψ(t)〉代入薛定谔方程中,得到

图1 量子态演化路径规范变换示意图

(22)

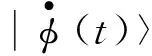
(23)

就受迫谐振子(1)而言,如果采用不变算符法,不变算符是系统对易物理量中的一个,所以哈密顿算符的本征态可以由不变算符本征态|Ik(t)〉的规范变换得到[13],即|φk(t)〉=eiαk(t)|Ik〉.将它代入薛定谔方程,得到的因子:

(24)

根据前面关于几何相位的论述,如果|Ik(t)〉周期性演化,即在希尔伯特空间中的轨迹是闭合曲线,那么式(24)右边第一项代表几何相位,第二项是动力学相位.如果仅仅是循环演化,就不能这么简单地认定.因为对量子态|Ik(t)〉规范变换的目的是定义明确的相位αk.如同式(20)中的相位因子δ(t),反映了系统实际演化的一部分.在此基础上再次进行规范变换,得到一条闭合路径,才能定义式(23)中那样的几何相位.

几何相位是由量子态的演化路径决定的,循环演化中存在几何相位,一般意义上的非循环演化,即初态和末态不在同一条射线上,也会有几何相位.虽然不能把这种情况的几何相位定义为式(23)右边第一项的形式,不过可以从中找到相应的计算方法.既然其中几何相位具有规范不变性,那么末态和初态的相位差与动力学相位的差也是规范不变的.非循环演化情况下,可以定义一个类似的规范不变量.作规范变换|ψ(t)〉→|ψ′(t)〉=eig(t)|ψ(t)〉,那么有

(25)

arg〈ψ′(t0)|ψ′(t)〉=

arg〈ψ(t)|ψ(t0)〉+[g(t)-g(t0)]

(26)

而动力学相位是

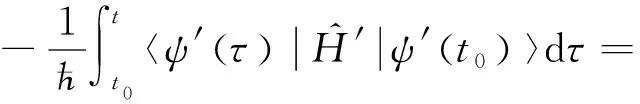
(27)

由式(26)和式(27)可知

(28)

是一个规范不变量,因而可以用来计算非循环演化时的几何相位.可见与式(23)是相通的.

现在我们开始具体计算受迫谐振子的几何相位.假设外力是周期性的,f(t)=sinω0t,式(20)中的相干态参数

(29)

当谐振子的振动频率与外力的频率之比是有理数时,|ψ(t)〉循环演化.从式(23)知道相应的几何相位是

(30)

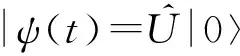
(31)