蜃景形成的原理及实验验证
2021-11-06韩润泽
韩润泽
(北京师范大学 物理学系,北京 100875)
海市蜃楼,又称蜃景,是光线经过不同折射率的介质层发生连续折射或者发生全反射时出现的一种光学现象.
蜃景成因的主流观点是光线经过多次折射,入射角不断增大,最后出现全反射改变光路方向[1,2],也有观点认为上现蜃景是由于掠入射导致的镜反射引起的[3].人造蜃景的方法主要是利用自由扩散法[4-7],且大多数文献只是通过扩展光源照射得到蜃景为止,暂无通过激光显示光路来验证蜃景形成原因的.
蜃景常见的是上现蜃景、下现蜃景和复杂蜃景.复杂蜃景是变形的上现、下现蜃景以及一些其他蜃景(如侧向蜃景)的复杂叠加[8].本文将以上现蜃景为例进行理论和实验的验证,得到蜃景形成的一般原理.
1 光在介质中传播基本理论
1.1 光线轨迹理论推导
大气层分成同心球壳,每一球壳的折射率认为相同, 在任意相邻的两个球壳的分界面上, 发生折射现象.
由菲涅耳定律,设入射处折射率为n0,入射角为θ0.第i层的折射率为n(y),入射角为θ(x,y),有
即有
(1)
以射入点为原点,沿容器向上开口为y轴正方向.在垂直于y轴的平面内,沿光线在该平面上的投影的方向为x轴建立坐标系.如图1所示.
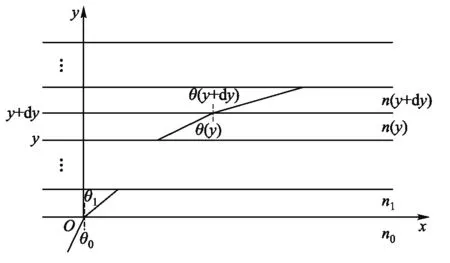
图1 光线传播轨迹示意图
在y处的导数表达式为
代入式(1)得
(2)
通过2.2节配置溶液的方法,n(y)满足
(3)
折射率渐变溶液.其中a、b为溶质决定的参数;M0%为起始溶液的质量百分数;S、V为与装置有关的常量. 记

(4)
n0sinθ0=E
(5)
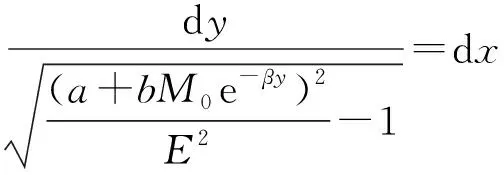
(6)
由全反射限制,取E>a积分得
C为积分常量. 条件入射点(0,y0),积分得
称为光线方程. 式(7)中

(8)
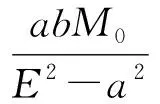
(9)
a、b、β、E由式(3)、(4)、(5)决定.
由反三角函数定义域, 得
(10)
则y的最大值ym恰为光线发生全反射时的y值. 即n(ym)sin90°=n0sinθ0. 代入ym,得到对应的全反射处的x值满足
(11)
1.2 一种特定折射率渐变溶液的成像规律
由NaCl溶液折射率n与其质量百分数的经验公式[9],得到式(3)中的参数:
a=1.333 1±0.000 5;
b=0.001 85±0.000 03
(12)
并取β=7.955/m,M0=16.
激光以不同入射角从y0=0.03m处射入溶液,光线发散,所成像为在特定观察点的光线切线的交点,故为虚像. 用Matlab模拟入射光线在溶液中的光路及物点对应的成像点,如图2所示. 盛放配置溶液的容器长1m,物贴在容器一侧的器壁上,人在另一侧观察.
观测点的横坐标一定时,对于物体的两端分析,探究成像情况. 由于光射出容器后沿直线传播,且观测人眼离容器壁很近,故取观测点横坐标为x0=1m,物点纵坐标分别为y0=0.03,0.09m. 箭头所指的圈中为对应物点的像点位置,如图2所示.
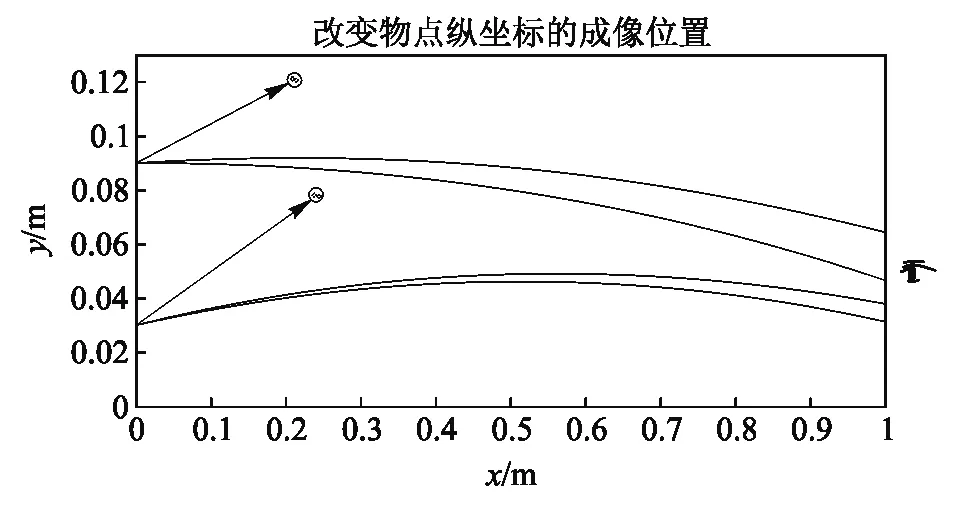
图2 改变物点纵坐标模拟成像位置
通过图2可知,物点越高像点越高,所以不论物的纵坐标在何处,只要光线透过溶液且切线的交点近似为一点,得到的都是正立的虚像.
2 光在非均匀介质中传播的实验
2.1 实验装置
改进指数分布法配置溶液装置示意图如图3所示.由四部分组成,分别是水管、混合槽、观景槽、内外双层开缝塑料管. 水管通入可调恒定水流,通过调节水流流量与混合槽流出水流流量相等来使混合槽水位不变. 混合槽实验前装入配置好的已知初始质量百分数的溶液,高度适宜.
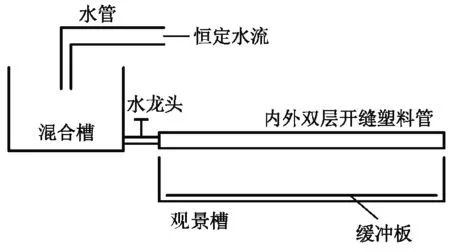
图3 配置装置示意图
观景槽实验前调平,以保证折射率分界面水平.在实验开始前,观景槽内放入缓冲板.缓冲板是与观景槽槽底等大的打孔泡沫板,可以漂浮在水面上,一定程度上使水流相对平稳落入观景槽.
在混合槽一侧的水龙头加上内外双层开缝塑料管(剖面图如图4所示),内部小口径塑料管上侧开口,保证其灌满后再均匀溢出.外部大口径塑料管下侧开多个槽使溶液流出. 水龙头与塑料管的规格大小为:内管外径和外管内径与水龙头的内外径恰好相同,避免水的泄漏.实验开始前,内外双层开缝塑料管的末端需要封住,避免实验时溶液外流.

图4 内外双层开缝塑料管剖面图
2.2 配置观景槽溶液的原理及步骤
水管和水龙头流量相等,记为Φ.混合槽内装入质量百分数为M0,体积为V的食盐水. 设t时刻混合槽内盐水质量百分数为M(t),dt时间内槽内食盐的增量为VdM,从混合槽排出的盐水质量百分数也为M(t),dt时间内从混合槽排出盐量为Φdt·M.在混合槽内食盐增量就等于该槽食盐的排出量,因此有
VdM=-Φdt·M
(13)
(14)
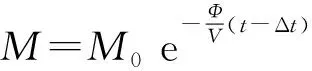
(15)
令t时刻观景槽盐水的高度为y,底面积为S,则
(16)
联立式(15)、式(16),得
(17)
其中M%为混合槽内盐水质量百分数,S为观景槽的底面积,V是混合槽中液体的体积,M0%为混合槽中溶液初始质量百分数,对于食盐水一般是10~20%[10].
2.3 实验步骤
1) 按图3摆放实验装置,保证观景槽高度适宜观看.
2) 打开水管和混合槽水龙头,调整二者流量使混合槽内水位达到不随时间改变.关闭水管和水龙头,倒出混合槽内的水并擦拭干净.
3) 在混合槽内注入盐水,质量百分数M0=20左右.标记混合槽水位,保证配置过程高度不变.
4) 同时打开水管和混合槽水龙头.用搅拌棒在混合槽内不断搅拌.目视混合槽标记处,保证混合槽水位高度不变.
6) 去掉除观景槽以外的所有装置,配置完成.
2.4 实验数据提取方法
配置完溶液后,激光如图5方式斜入射,之后用Tracker软件提取照片中光路的数据点,进行数据分析. 提取数据点具体方法如下.
1) 用win10电脑自带的图片转视频功能,将一张如图5的光路照片转为时长约为30 s的MP4文件.

图5 激光笔斜上入射
2) 打开Tracker,导入转换好的MP4文件.
3) 建立坐标系,设定定标尺和质点. 把原点设置在视频中长方体容器左下角,坐标系x轴与容器底边重合. 利用定标尺,把容器长度定为1 m. 点击工具栏中的创建质点,按住Shift键出现一个小方框,将方框中心置于y轴上的光线入射点. 点击之后就将质点A创建在了方框正中心.
4) 手动逐帧在光线上标定质点,每点一次鼠标就会标定一帧,每帧质点都在上一帧基础上右移3 mm左右,直到把整个光线标定出来.
5) 将提取的x,y坐标导入Excel,进行数据处理.
如图6所示,将提取的数据点还原光路,与理论计算光路对比可初步判断理论的可靠性.其中误差棒表示的是每一点测量的不确定度,可以看到误差棒的数量级为1 mm.
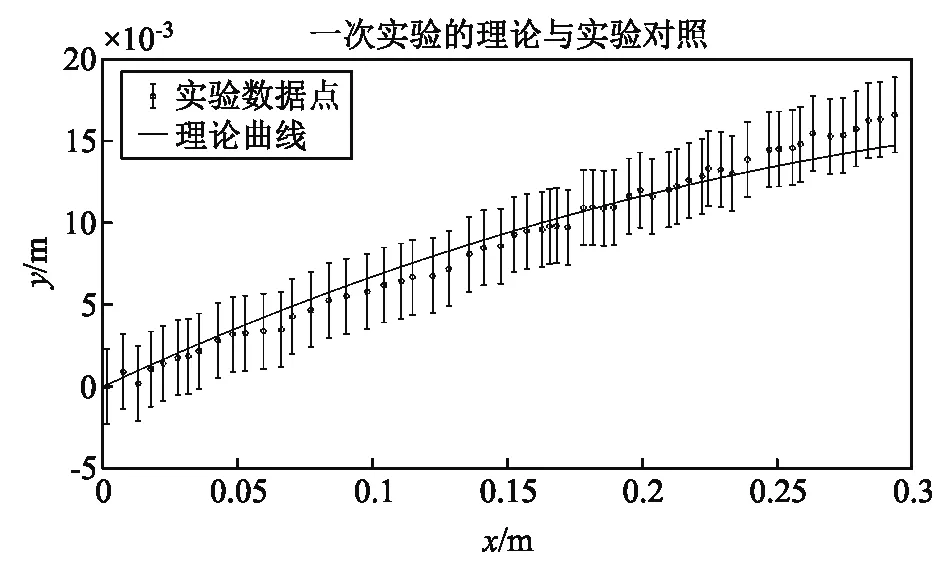
图6 一次实验的理论与实验曲线对照图
图7为物点纵坐标为y0=0,观测点横坐标x0=0.3 m,即与图6实验参数吻合情况下理论模拟的不同入射角的光线和成像位置. 箭头所指的圈为像点位置.该处成像原理并不是全反射,而是光线的过度折射.
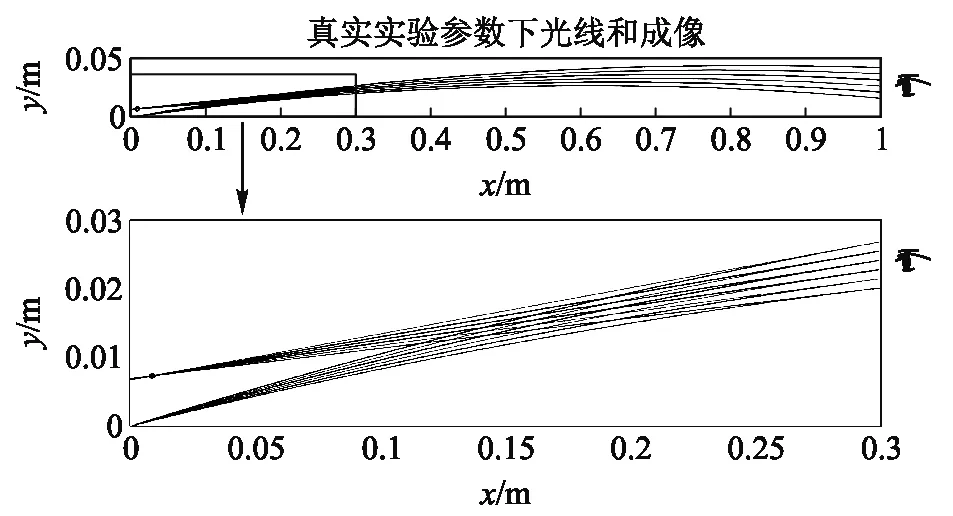
图7 在真实实验参数下的光线和成像图
2.5 实验数据处理方法
B=PA
(18)
记A、B正比关系拟合的斜率为k,则
(19)
选用斜率k作为对照理论值与实验值的依据.
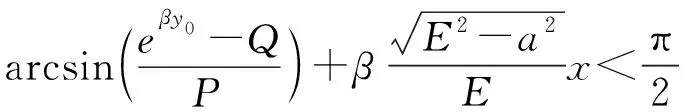
(20)
的数据进行拟合,同时设置截距为0.
这个限制严格来说会导致全反射之后的光线无法与文中理论直接对照,但是由于光路的对称性,只考虑全反射之前的理论实验对照依然是可行的.
实验中靠上层的溶液与计算得到的溶液质量百分数符合度较低,主要原因是溶液越靠上,相邻层的变化越小,扩散作用会导致上层几乎变为均匀溶液,折射率没有变化,故而光线进入该区域后不再向下弯折.
2.6 实验数据分析
条件为:β=8.594/m,y0=0,x0=1 m,a=1.333 1,b=0.001 85,M0=16,ρ=1.116 g/cm3[11],改变入射角进行实验. 斜率k的理论与实验对照见表1,图8为入射角θ0=85.64°条件下B-A图. 可以看出,各次实验的相对误差都是比较小的.

表1 改变入射角θ0时斜率k的理论与实验对照
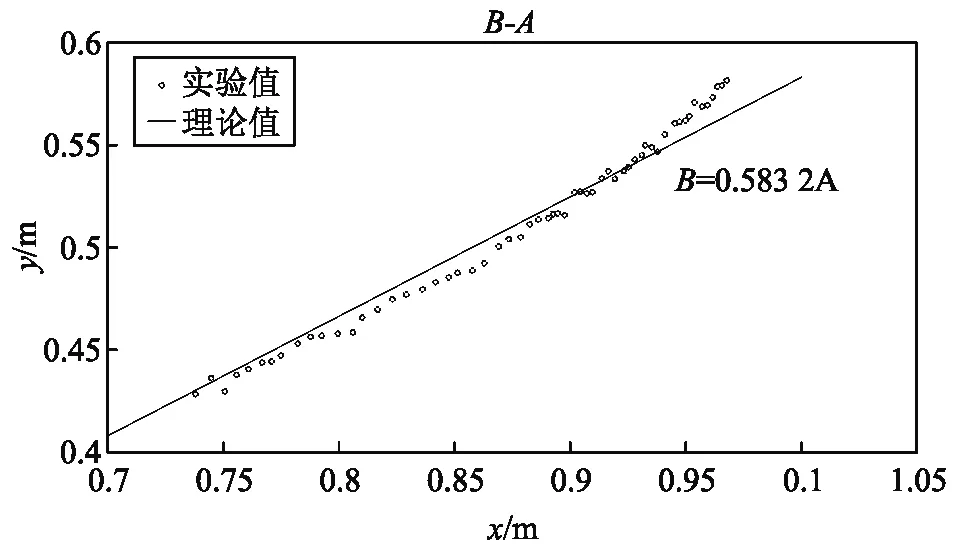
图8 θ0=85.64°条件下B-A正比关系拟合图
2.7 误差分析
实验中直接测量的物理量为:观景槽的长p,观景槽的宽q,射入点纵坐标y0,配置食盐水的食盐质量mNaCl,水的体积Vwater,构成射入角的短边h,长边d,标定点的坐标x、y.
直尺测量物理量为p、q、y0、h、d,不确定度为

(21)
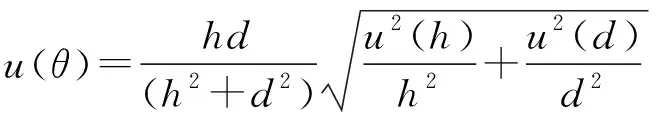
(22)
代入数据计算得u(θ)的数量级为10-3rad,故记u(θ)=0.001 rad;mNaCl由机械天平测量且除食盐外含有0.2%杂质(如KCl,I等),故记不确定度u(mNaCl)=5g,Vwater由量筒测量,不确定度u(Vwater)=5ml.
用2.4节提取数据点的方法,x、y数据精度主要受Tracker内置算法,手动标点误差以及照片视差的影响. 查阅Tracker参考手册得到信息:当照片像素高时对应坐标误差很小,虽然没有给出具体数据,但由Tracker可以适用于测量单缝衍射[12],有理由估算上述三种误差带来的极限误差和不超过1 mm.故u(x)=u(y)=1 mm.
由式(12),得u(a)=0.000 5,u(b)=0.000 03,将上述所有不确定度合成,代入不确定度计算公式
(23)
其中
(24)
(25)
(α=p,q,y0,a,b,mNaCl,Vwater,θ), 得到的不确定度如下表.
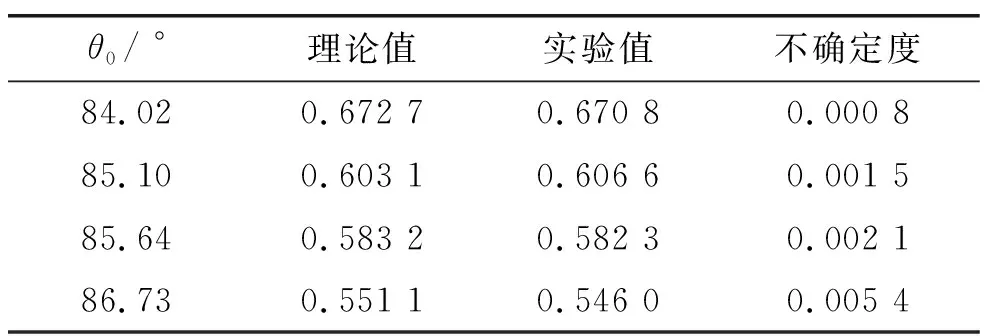
表2 改变入射角θ0的斜率k实验不确定度
由于理论计算得到的值基本上在实验值的2σ区间内,所以实验结果是比较可靠的.
溶液从内外双层开缝塑料管落入观景槽时不可避免会对配制溶液产生扰动,得到的溶液与理论计算有差异.这个差异是不可控的,而且是主要误差来源.
3 讨论
首先讨论激光热效应的影响. 通过估算,在实验时间内水升高的温度小于ΔT=0.36℃,在这个温度变化范围内,折射率的变化为10-5数量级[13],而配制溶液折射率精度为10-3,故激光热效应带来的影响可以忽略不计.
其次讨论配置溶液的稳定性和溶液的横向折射率对实验的影响. 由于食盐溶液的折射率不易无接触测量,而溶液的稳定性与溶质的扩散系数有关,考虑到食盐和葡萄糖的扩散系数均为10-9数量级,我选择利用葡萄糖的旋光性测量相同折射率渐变葡萄糖溶液的折射率.
一是在5处竖直方向坐标不同的位置用消光法多次测定浓度(如图9),二是在同一高度测量多处浓度. 偏振片A不动的情况下,消光偏振片B角度变化小于1°. 由葡萄糖溶液浓度和折射率经验公式得到[14,15],折射率变化量为1.4*10-5(20 ℃),配置溶液折射率精度为10-3,故在实验过程中自由扩散影响和横向折射率的影响均可忽略不计.
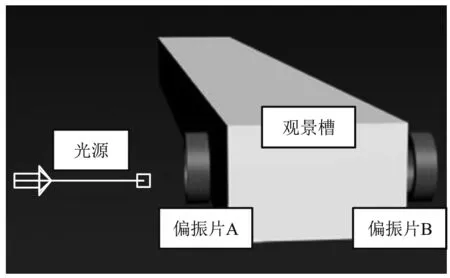
图9 旋光法测溶液浓度示意图
4 总结
用激光照射有折射率渐变流体,光路为
对于折射率n与高度y满足式(3)的溶液,从(0,y0)入射,光路方程为
其中P、Q、a、β、E由式(8)、(9)、(12)、(4)、(5)决定.
由于负指数梯度的折射率变化与大气类似[16],所以通过溶液成像的模拟和实验可以归纳上现蜃景的总体规律:上现蜃景物和像大小关系不能确定,且大部分为正立虚像,
