基于COMSOL有限元法的涡流探头线圈仿真

2021-11-06邱建东祁育栋许向东

兰州交通大学学报 2021年5期

邱建东，祁育栋，许向东

(兰州交通大学机电工程学院，兰州 730070)

无损检测是建立在现代科学技术基础上的一门综合性学科，是指在不损害被测对象的前提下，通过电磁场导致的声、光、热、力学等参数的变化为依据，进而判断被测对象表面或内部的物理性能、状态特性以及内部结构[1].目前，工程中常用的无损检测方法包括：超声波检测、射线检测、涡流检测、磁粉检测和渗透检测.其中，涡流检测技术因具有非接触、无需耦合剂、检测速度快、操作简单、对检测表面要求低以及对人体无辐射危害等优点，在金属材料、零件和装备的质量与结构完整性检测与评估中发挥着重要的作用，涡流检测技术成为了最广泛使用的无损检测技术之一[2-5].

涡流检测技术是一种基于电磁感应原理的无损检测方法，利用探头和被测试件之间的磁场能量耦合实现对被测量的检测，特别是对试件完整性的检测[6].涡流探头作为涡流检测系统中的核心部件之一，承担着产生激励磁场和拾取试件信息的任务[7]，探头结构的优化一直是涡流检测系统研究中的热点.文献[8]中采用有限元仿真软件，提出了一种包含均匀多匝线圈、金属试件板以及封闭式空气域的电涡流无损检测建模方法；文献[9]中介绍了电涡流传感器核心性能优化的基本原理和关键技术，对相关研究的发展趋势进行了初步的构想和展望；文献[10]中采用ANSYS软件仿真优化了矩形线圈的尺寸，据此设计了一种矩形-圆形探头，有效抑制了提离带来的影响；文献[11]中采用有限元法建立了仿真模型，以差分信号峰值为特征分析了脉冲激励参数和激励线圈参数对检测灵敏度和分辨率的影响规律；文献[12]中提出并开发了一种新型的环向偏心Bobbin探头，该探头兼具轴向扫描和偏心环向扫描的功能,能够对小径管缺陷的多重信息进行有效检测.由上述研究可见，涡流探头中磁感应强度大小、试件中涡流分布情况与探头灵敏度高低有密切的关系，从很大程度上影响探头的性能.基于此，本文从影响探头性能的源头即磁感应强度和涡流分布两个因素以及线圈的阻抗三方面进行综合分析，利用COMSOL有限元仿真软件，通过构建不同参数的线圈模型，通过观察线圈周围磁场的分布、试件中涡流的特性以及线圈实部和虚部变化来对探头检测性能进行分析，并对仿真结果和已有理论分析结果进行了对比验证.

1 涡流检测理论

1.1 涡流检测原理

涡流检测是涡流效应的一项重要应用.根据电磁感应原理，当一个通有交流电的探头线圈靠近或放置在被测试件上时，产生的初级交变磁场就会与被测试件发生电磁感应作用，在试件中感生出的电流，称之为涡流.根据楞次定律，试件的涡流同样会产生二次磁场，并与探头线圈发生电磁感应作用，进而在线圈上感生电压.线圈中的总电压是原激励电压与涡流感应电压的矢量之和.当试件中出现缺陷或其电导率、磁导率、形状、尺寸等发生变化时，会对涡流的强度和分布产生影响，而涡流的变化又会引起线圈感应电压的变化.因此，通过检测探头线圈电压的变化，就可以判断出导体试件是否存在缺陷，其原理如图1所示.

图1 涡流检测原理图Fig.1 Principle of the eddy current testing

1.2 阻抗分析法

为了分析被测试件的性质与探头线圈参数之间的关系，研究者提出了包含两个线圈耦合的变压器耦合式互感交流电路等效模型，并利用电压变化和阻抗变化之间的相似规律，通过线圈阻抗的变化来反映电压效应，该方法为目前在涡流检测中广泛运用的阻抗分析法，其线圈耦合的等效电路图如图2所示.

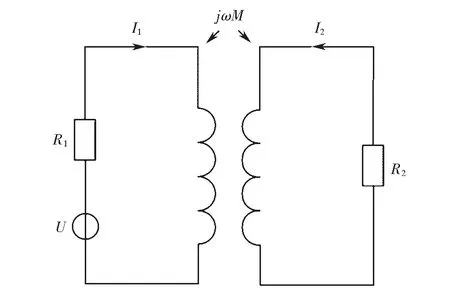
图2 等效电路图Fig.2 Equivalent circuit of the model

图中：R1，L1分别为探头线圈的电阻和电感，R2，L3分别为被测试件的电阻和电感；M为探头线圈与被测试件之间的互感系数；U为探头线圈两端的激励电压.

由基尔霍夫电压定律可得原、副边电路中的电压方程为：

(1)

联立(1)式中的方程组，可求得探头线圈的等效阻抗为：

(2)

进而可求得线圈中实部的等效电阻和虚部的等效电感分别为：

(3)

式中：等效电阻R是互感系数M的函数.可以看出，当探头和被测试件之间的距离减小时，M增大，这一变化与被测试件是否为磁性材料无关.等效电感L受两种效应的影响：L1受静磁效应的影响，即与被测试件是否磁性材料相关；L2受涡流效应的影响，且两种效应对等效电感所产生的作用是相反的.因此，当被测试件为软磁材料时，线圈中等效电感主要受静磁效应的影响，探头靠近被测试件时，探头的等效电感量增大；当被测试件为非铁磁性材料或硬磁材料时，线圈中等效电感主要受涡流效应的影响，探头靠近被测试件时，探头的等效电感量减小.

1.3 趋肤效应

在涡流检测问题中，涡流是由衰减的磁场感应所产生的，所以必然会导致导体试件内部涡流的衰减，把这种电流随着深度的增大而衰减且电流密度明显集中在导体试件表面的现象称为趋肤效应.涡流渗入导体内的距离称为透入深度，定义涡流密度衰减到其表面值的1/e(约36.8%)时的透入深度为标准透入深度，也称趋肤深度.涡流透入深度计算公式[13-14]为：

(4)

式中：δ为渗透深度，单位为mm；f为交流电流的频率，单位为Hz；μ为导体的磁导率，单位为H/m；σ为导体的电导率，单位为S/m.

2 涡流检测探头线圈有限元模型

2.1 几何建模

COMSOL软件中附加的“AC/DC模块”可对在时变磁场中产生大量感应电流的导体及其它有损材料进行建模.根据探头结构的对称性特点，建立如图3所示的涡流探头检测系统的等效模型.所建模型中包含了两类边界条件:第一类边界条件为强边界条件,具体指图中平面区域的周边,代表了求解区域的范围.第二类边界条件为模型中各种媒介之间的交界条件,称为自然边界条件,只需将各边界之间设为连续变化,由泛函求极值自动满足.

2.2 材料选择

空气场所选材料为空气，线圈所选材料为铜，被测试件所选材料为不锈钢，所选各种材料的电导率γ、相对介电常数εr和相对磁导率μr如表1所示.

表1 材料参数Tab.1 Material parameters

2.3 物理场的添加

在COMSOL软件中，选择低频电磁场模块中的磁场,将其添加到模型中作为物理场.在磁场中选择均匀多匝线圈物理场以施加电压和确定线圈的匝数.选择线圈匝数为500匝，选择激励为1 V的电压信号，涡流探头模型选用狄利克莱边界条件，即磁矢势为0.

2.4 网格划分

COMSOL软件可以提供三角形和四边形等网格单元，具有自由网格划分、自适应网格划分等网格划分功能.由于将文中导体试件暴露在时变的电磁场中时会产生趋肤效应，且探头线圈周围的磁场分布和被测试件中感应涡流的分布情况是本次研究的重点内容，所以在确保求解精度的前提下，对具有规则形状的探头线圈和被测试件采用映射网格，对空气域采用自由三角形网格，模型的网格划分图如图4所示.

图4 模型的网格划分图Fig.4 Mesh of the model

2.5 有限元模型的求解与后处理

输入激励频率，对模型进行求解设置，通过变换参数，可获得感应磁场的磁场分布、被测试件中的感应涡流分布、探头线圈的阻抗，进而分析激励频率、提离和线圈尺寸对探头检测性能的影响.

3 仿真结果与分析

3.1 激励频率对涡流探头性能的影响

激励频率的大小对探头周围磁感应强度、被测试件中涡流的大小以及涡流的渗透深度都有着重要的影响，进而影响着探头的检测性能.因此，合理地选择激励频率大小尤为重要.本文选用50、100、200、500和1 000 Hz五种不同激励频率的电流信号进行加载，被测试件中涡流的分布如图5所示.

探头线圈阻抗与激励频率的关系如图6所示.

由图5可知，当激励频率为50 Hz时，涡流能够渗入试件的深层部位，随着激励频率的增大试件中涡流的分布区域不断减小，表明探头能检测到的缺陷深度也不断变浅.结合公式(4)，随着激励频率的增大，趋肤深度不断减小，理论分析与仿真结果一致.而涡流面密度的最大值随着激励频率的增大而增大，表明探头的灵敏度不断升高.由图6可知，线圈阻抗实部虚部都随着激励频率的增大而增大，即探头线圈的等效电阻和电感都增大，且电抗与激励频率呈线性关系.结合公式(3)，电感L随着激励频率的增大而减小，由于X=ωL=2πf，此时，ω占据主导地位，L减小的值很小，因此电感和激励频率成正比.为了确保检测系统较高的灵敏度和实现对较深层缺陷的检测，后续分析选择100 Hz的激励频率进行加载.

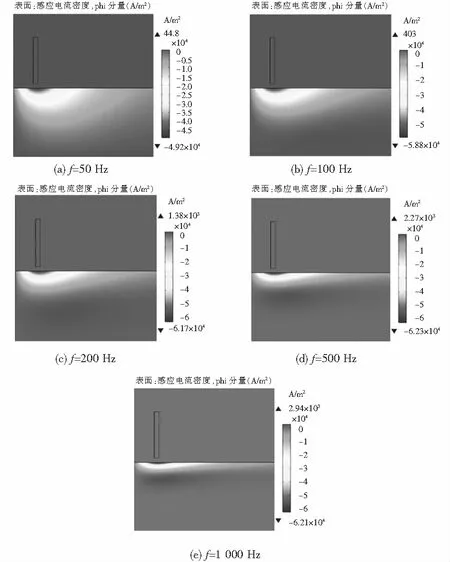
图5 激励频率变化时被测试件中的涡流分布Fig.5 Eddy current distribution of object under different excitation frequencies

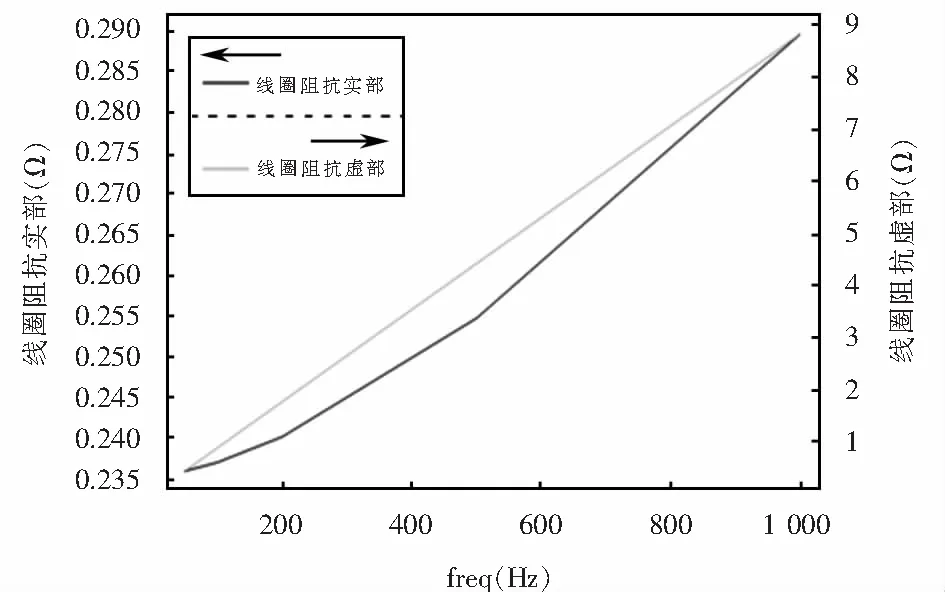
图6 探头线圈阻抗与激励频率的关系Fig.6 Relationship between coil impedance and excitation frequencies

3.2 提离对涡流探头性能的影响

提离是指涡流探头与被测试件表面之间的距离.当提离变化时，探头和试件之间的相互作用程度也会随之发生变化，从而影响探头的检测信号，这种现象被称为提离效应，它所产生噪声信号会对缺陷信号的拾取产生很大的干扰，抑制提离效应一直是涡流检测中迫切需要解决的问题.选择探头线圈匝数为500匝，内径为4 mm，外径为5 mm，高度为10 mm，用100 Hz的激励频率进行加载，当提离a分别为0.5、1.0、2.0、3.0和5.0 mm时，探头线圈周围磁感应强度的分布和被测试件中涡流的分布如图7所示.

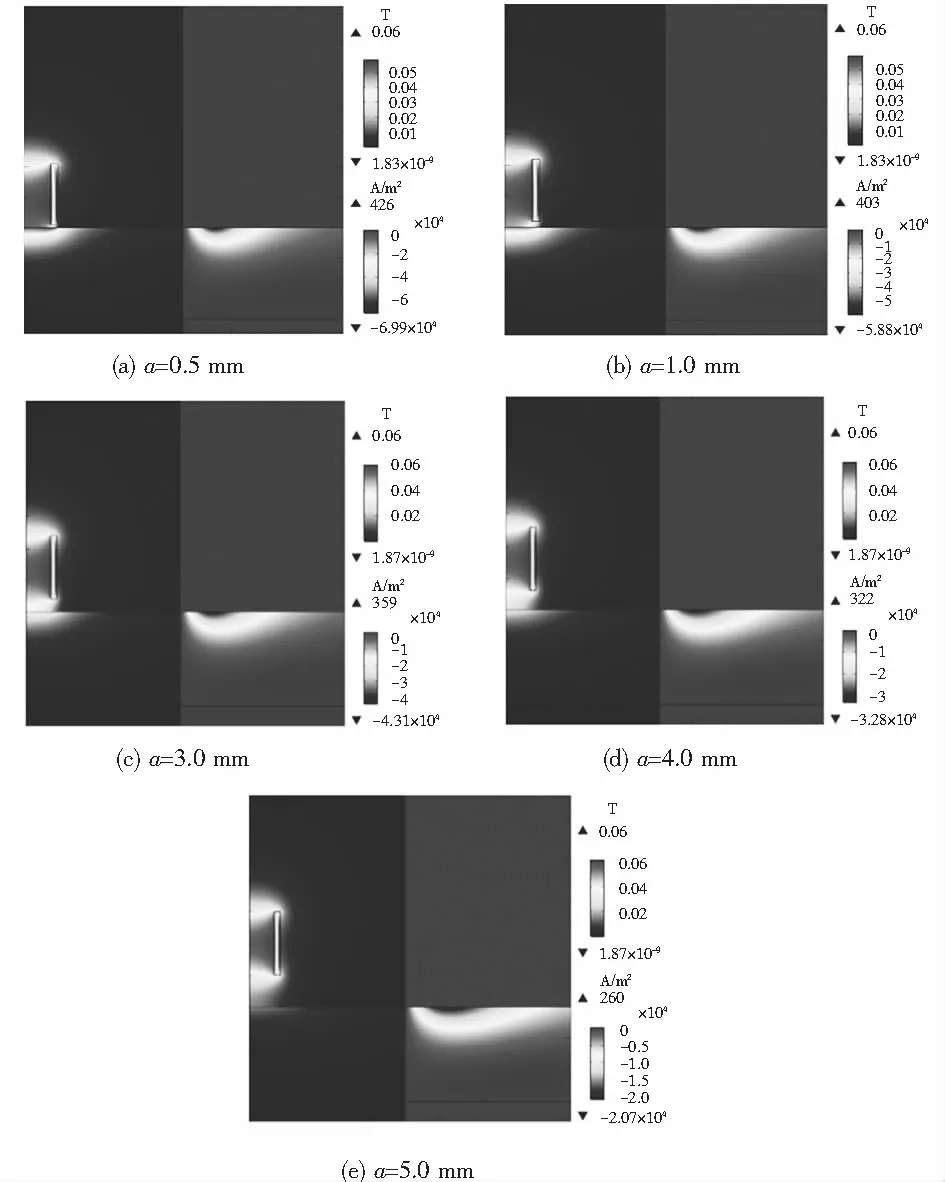
图7 提离变化时探头线圈周围磁感应强度的分布和被测试中涡流的分布Fig.7 Magnetic field distribution around the probe coil and eddy current distribution of object under different lift-off distances

探头线圈阻抗与提离的关系如图8所示.

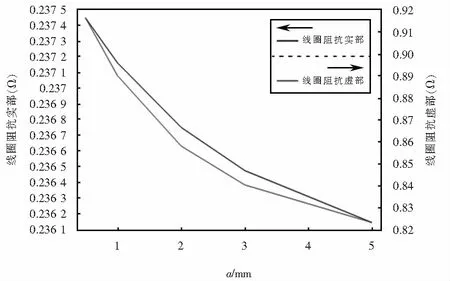
图8 探头线圈阻抗与提离的关系Fig.8 Relationship between coil impedance and lift-off distances

由图7可知，提离a增大时，探头线圈周围磁场的分布基本不变，磁感应强度的最大值稳定在0.06 T左右，被测试件表面的磁感应强度逐渐减小，同时被测试件内电流密度的最大值也逐渐减小，且减小的速率随着提离的增大而增大.由图8可知，探头线圈等效电阻和电感均随着提离的增大而减小，这是互感系数减小的缘故.因此，增大提离会使探头检测的灵敏度下降，所以在实际检测中尽可能的减小提离大小.

3.3 线圈几何参数对涡流探头性能的影响

探头线圈几何参数的确定是涡流探头设计中的重要环节.文中利用有限元法研究线圈几何参数与线圈磁场和被测试件中涡流分布的对应关系及变化规律，据此来分析探头线圈几何参数对探头检测性能的影响.

3.3.1 线圈内径对涡流探头性能的影响

保持激励频率大小为100 Hz，提离为1 mm，探头线圈外径为5 mm，线圈高度为10 mm，线圈匝数为500匝，当线圈内径r1分别为0.5、1.0、2.0、3.0和4.0 mm时，探头周围磁感应强度的分布和被测试件中涡流的分布如图9所示.

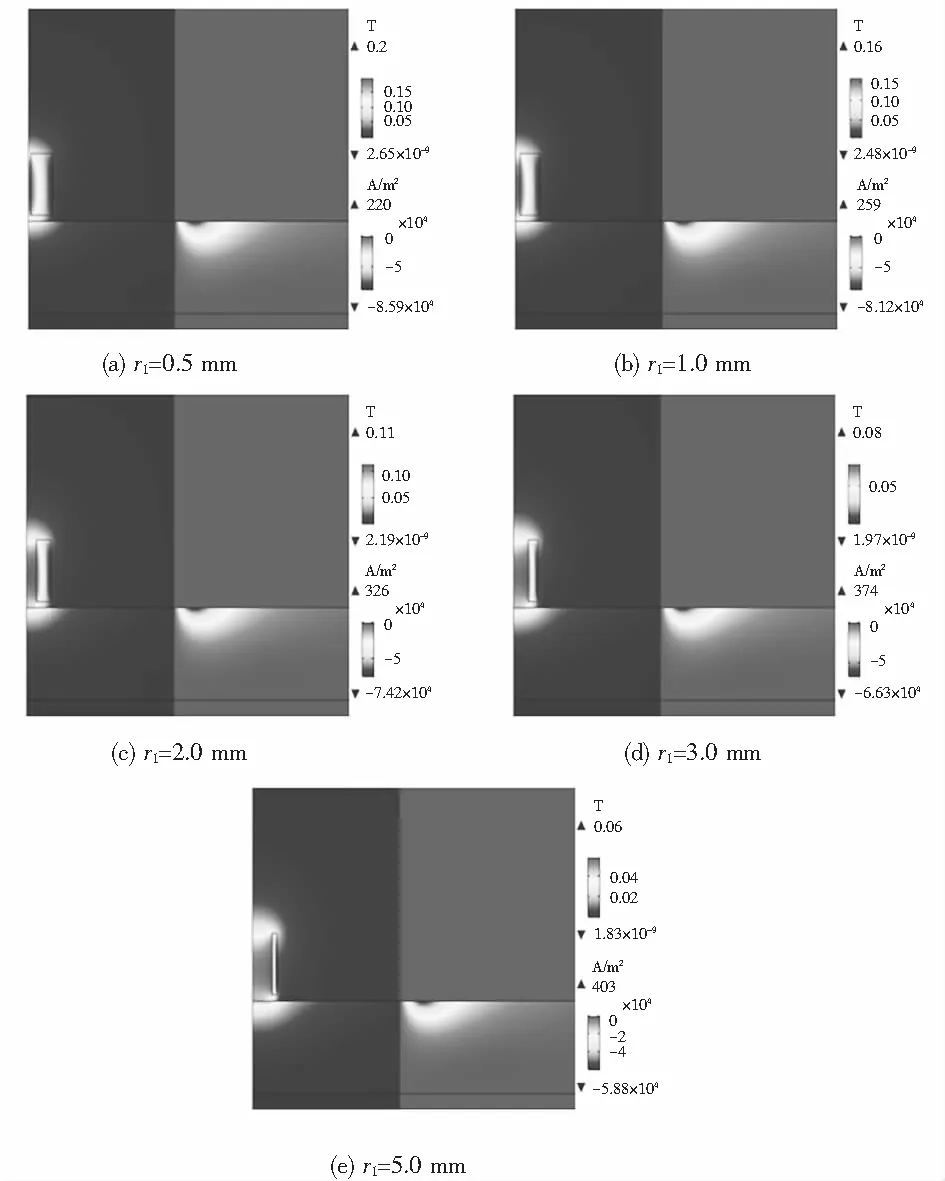
图9 内径变化时探头线圈周围磁感应强度的分布和被测试中涡流的分布Fig.9 Magnetic field distribution around the probe coil and eddy current distribution of object under different inner radio distances

涡流探头线圈阻抗与内径的关系如图10所示.

由图9可知，保持线圈的外径和高度不变，线圈内径r1增大时，被测试件磁感应强度的最大值从0.2 T降至0.06 T，而感应涡流密度的最大值从220 A/m2逐渐增大到403 A/m2，被测试件中磁感应强度和感应涡流区域有略微的外扩.由图10可知，线圈阻抗实部和虚部的值都随着线圈内径的增大而增大.因此，增大内径会使得探头的灵敏度提高.

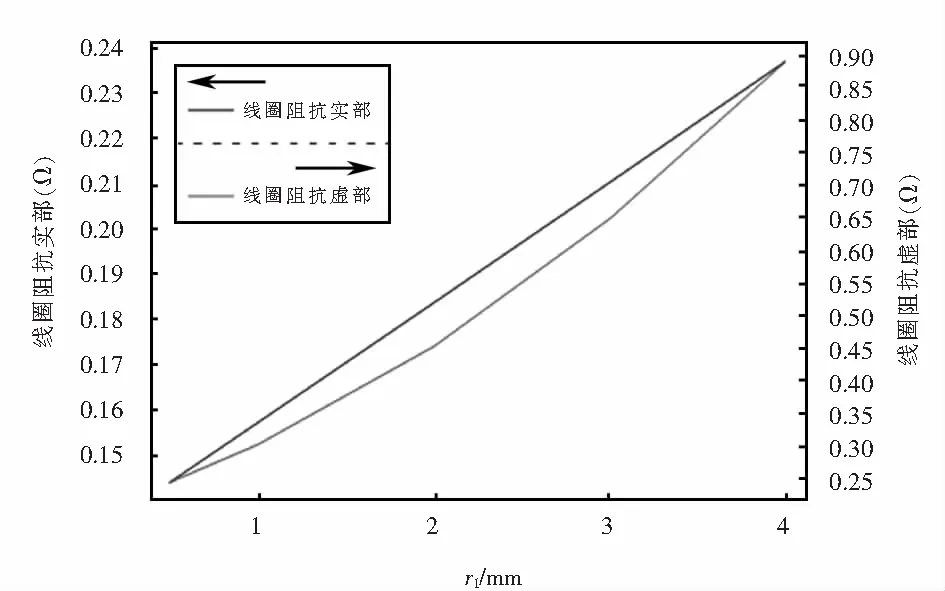
图10 探头线圈阻抗与内径的关系Fig.10 Relationship between coil impedance and inner radius distances

3.3.2 线圈外径对涡流探头性能的影响

保持激励频率为100 Hz，提离为1 mm，探头线圈内径为4 mm，线圈高度为10 mm，线圈匝数为500匝，当线圈外径r2分别为5.0、6.0、7.0、8.0和9.0 mm时，探头周围磁感应强度的分布和被测试件中涡流的分布如图11所示.

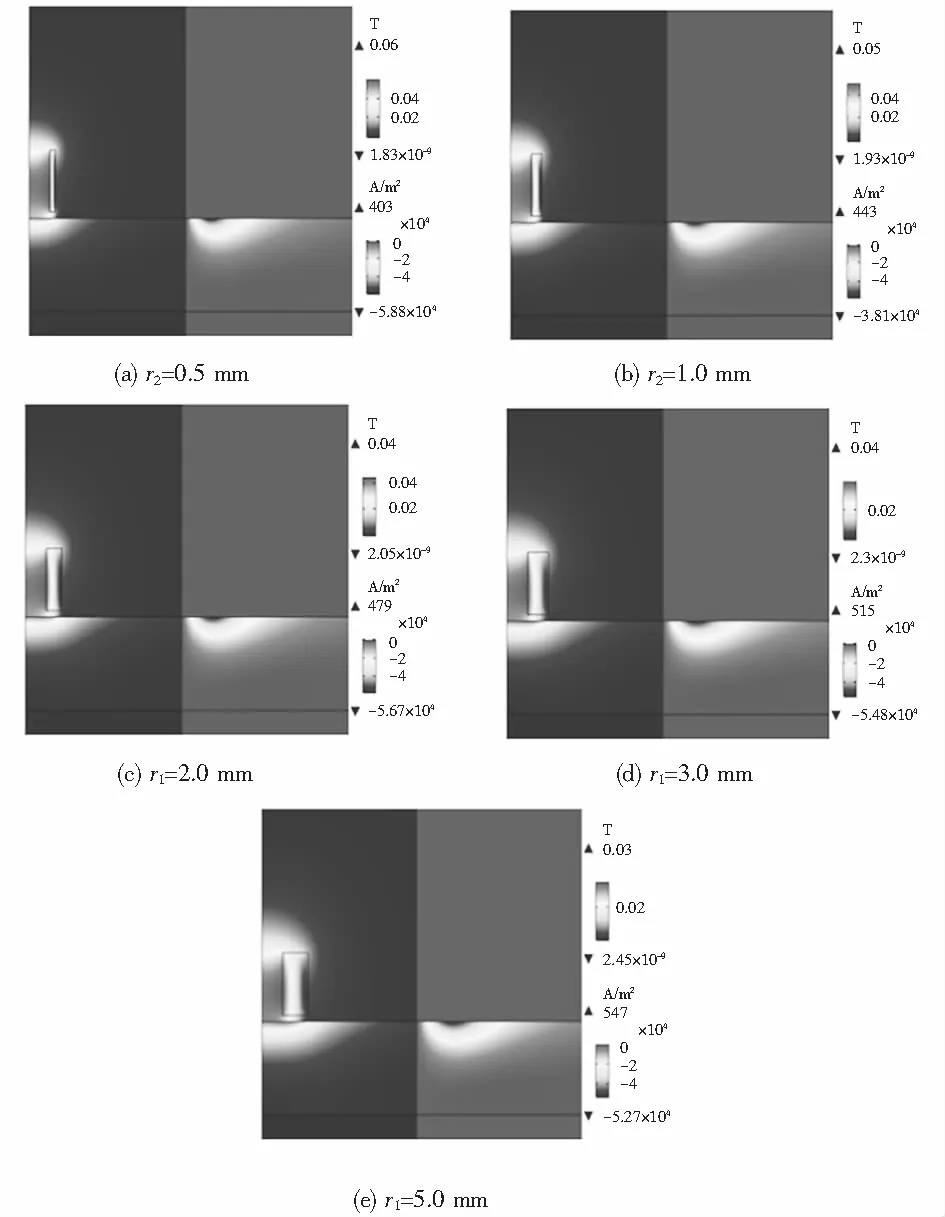
图11 外径变化时探头线圈周围磁感应强度的分布和被测试中涡流的分布FFig.11 Magnetic field distribution around the probe coil and eddy current distribution of object under different outer radius distances

涡流探头线圈阻抗与外径的关系如图12所示.

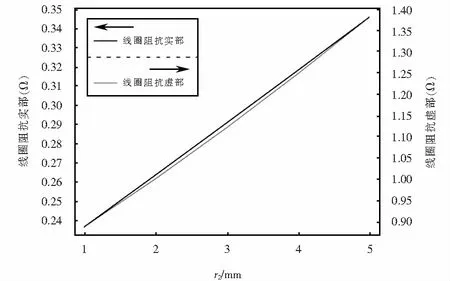
图12 探头线圈阻抗与外径的关系Fig.12 Relationship between coil impedance and outer radius distances

由图11可知，线圈外径r2增大时，磁感应强度的最大值从0.08 T降至0.03 T，感应涡流密度的最大值由403 A/m2增大到547 A/m2，且被测试件中感应磁场和感应涡流区域均明显增大，涡流渗透深度也增大.由图12可知，探头线圈的电阻和电感都随着线圈外径的增大而增大.因此，增大线圈外径有利于提高探头的灵敏度和检测被测试件的深层缺陷，设计探头线圈时，可适当增大线圈外径.

3.3.3 线圈高度对涡流探头性能的影响

保持参数激励频率为100 Hz，提离为1 mm，线圈内径为4 mm，外径为5 mm，线圈匝数为500匝，当线圈高度H分别为2.0、4.0、6.0、8.0和10.0 mm时，探头周围磁感应强度的分布和被测试件中涡流的分布如图13所示.

图13 高度变化时探头线圈周围磁感应强度的分布和被测试中涡流的分布Fig.13 Magnetic field distribution around the probe coil and eddy current distribution of object under different heights

探头线圈阻抗与高度的关系如图14所示.

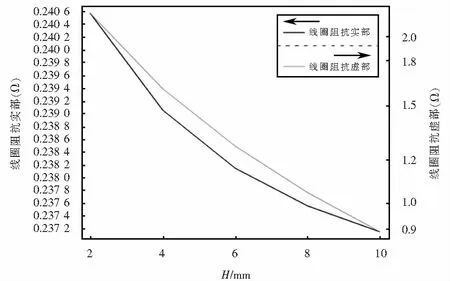
图14 探头线圈阻抗与高度的关系Fig.14 Relationship between coil impedance and heights

由图13可知，线圈高度H增大时，磁感应强度的最大值由0.08 T降至0.06 T,且磁感应强度的分布区域明显增大，被检测试件中感应涡流的分布区域变化不明显，而感应涡流的最大值先增大后减小.由图14可知，探头线圈的等效电阻和电感都随着高度的增大而减小.因此，线圈高度的过度增大对提高探头灵敏度有不利的影响，实际检测过程中应合理选择线圈高度.