基于LTE-R信号强度特征的列车位置指纹定位技术研究

罗 淼，党建武

(1. 兰州交通大学 自动化与电气工程学院，兰州 730070；2. 兰州交通大学 铁道技术学院，兰州 730099)

随着高速铁路系统快速建设，列车定位所面临的多隧道、难定位、精度低的问题亟待解决.目前的GPS(global positioning system)、GNSS(global navigation satellite system)、BDS(beidou navigation satellite system)等定位方式能够在平原开阔地带满足列车的精确连续定位，但并不适用于隧道环境下列车的高精度连续定位.针对这一问题，有学者提出采用BDS/GSM-R(global system for mobile communications-railway)组合列车定位方法，并通过神经网络拟合出列车的行驶路线实现列车的连续精确定位[1-2]，然而GSM-R不能在隧道内架设基站，采用GSM-R对列车进行定位时需要依靠架设漏泄同轴电缆，并且GSM-R在传输时延、吞吐量等方面越来越不能满足高铁列车的定位需要.文献[3]提出直接采用新一代铁路专用的移动通信系统LTE-R对列车定位，列车通过接受含有定位参考信号PRS(positioning reference signal)的LTE-R下行信道中的信号，采用TDOA(time difference of arrival)的方式实现列车定位，但是这种方式至少需要3个不同的固定基站才能实现，且由于铁路运营环境特别是隧道环境下，多径效应对测量时间的影响会造成较大误差，要减少误差就必须显著提高算法的复杂度或大规模的额外设备.而位置指纹定位可以只用1个基站，通过利用而不是消除多径效应引起的误差来完成定位[4-5].

本文采用基于LTE-R信号强度特征的位置指纹定位方式确定列车位置，以LTE-R的信号强度为基础，获取位置指纹的信息特征构建指纹空间，并通过WKNN(Kweighted nearest neighborhood)算法计算出列车位置.但列车在隧道中高速运行时容易受到多径效应的影响，测量得到的接收信号强度值RSS(received singnal strengh)会发生较大的变化，从而影响定位精度，因此本文采用CPSO(chaotic particle swarm optimization)算法对WKNN算法的权值进行优化，得到了一种CPSO_WKNN算法解算列车位置信息，以便有效的减少基于信号强度进行位置指纹定位列车时定位精度较低的问题.

1 基于LTE-R信号强度的位置指纹定位原理

位置指纹(location fingerprint,LF)是一种基于RSS的定位技术，其定位时的解算方法实质上是数据库相关算法(database correlation method,DCM)或模式匹配算法(pattern matching,PM)[6-7].无线信号的多径传播对环境具有很强的依赖性，并且呈现出很强的特殊性，因此对于每个位置上的无线信号而言是唯一的，位置指纹定位技术实际上就是将这些位置上的无线信号特征与位置信息相结合形成指纹条，并存储到数据库中，用实时采集的信号特征与已有的指纹库进行匹配，最终得出待定位目标的位置信息.这样的定位方式非常适合铁路隧道环境下对列车的定位，因此本文基于LTE-R的信号特征值采用位置指纹的方式对隧道环境下的列车进行定位，其定位原理如图1所示，图中BS(base station)表示基站，MS(mobile station)表示移动台，(?,?)表示待定位移动台的位置坐标.

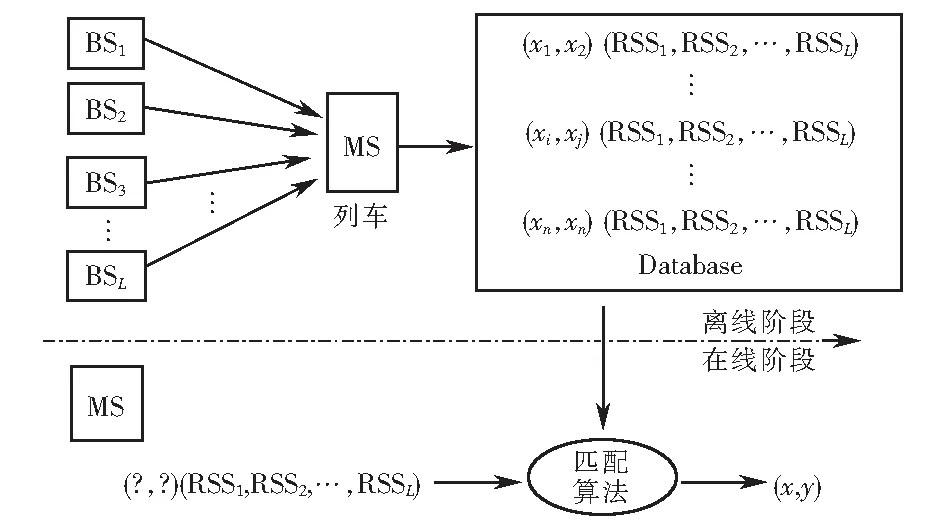
图1 基于LTE-R信号强度的位置指纹列车定位原理Fig.1 Location fingerprint train positioning principle based on LTE-R signal strength

位置指纹列车定位是以LTE-R的信号强度值为基础进行定位的，在采用位置指纹进行定位前首先需对LTE-R进行信道建模，同时搭建隧道环境下LTE-R位置指纹仿真场景来获取列车的RSS值，在进行位置指纹定位时主要包含两个阶段:第一阶段,离线阶段采集已知参考点PR(positioning reference)处所获得的不同接入点AP(aaccess points)的RSS值，建立离线指纹数据库；第二阶段,在搭建的仿真场景获取列车实时的RSS值，采用CPSO_WKNN算法解算列车位置.

2 LTE-R信道建模及场景搭建

2.1 LTE-R信道建模

LTE-R信道模型可采用标准传播模型 (standard propagation model,SPM)，文献[8]研究表明SPM模型更适用于LTE-R系统，对于列车实际运营的各种环境(平原、隧道或车站等)SPM模型都可以更准确的计算出路径损耗差异，SPM模型如式(1)所示.

L(d)=λ1+λ2lg(d)+λ3lg(hte)+λ4Diff+λ5lg(d)lg(hte)+λ6hre,

(1)

其中：λ1为偏移常量，取值为69.55；λ2是与距离d相关修正因子，一般为26.1；λ3默认值为5.83，表示基站有效高度的相关因子；λ4为信号传输过程中衍射的修正因子，在高铁隧道环境下取0.2；λ5为lg(d)lg(hte)项的修正因子，默认值为-6.55；λ6默认值为0，表示列车有效高度的修正因子；d为发射点到接收点三维直线距离，单位km；hte为基站发射天线有效高度，单位m；hre为列车的有效高度，单位m；Diff为信号传输过程中的衍射损耗.

由于式(1)给出的模型为一通用模型，结合高速铁路隧道的运行特点需要对其作出改进，由文献[9-10]知,列车运行速度小于500 km/h时，接收强度不会引起过多失真，实际车厢损耗为15～20 dBm，但是由于环境等影响还需加入某些修正因子进行修正.

速度修正因子δ1取值：速度小于200 km/h时δ1=0；速度大于200 km/h小于300 km/h时δ1=1；速度大于300 km/h时δ1=3.

LTE-R网络修正因子δ2取值：郊区δ2=-5；平原δ2=-20；山岭δ2=15；隧道δ2=-15.

环境修正因子δ3取值：服从N(0,2)正态分布.

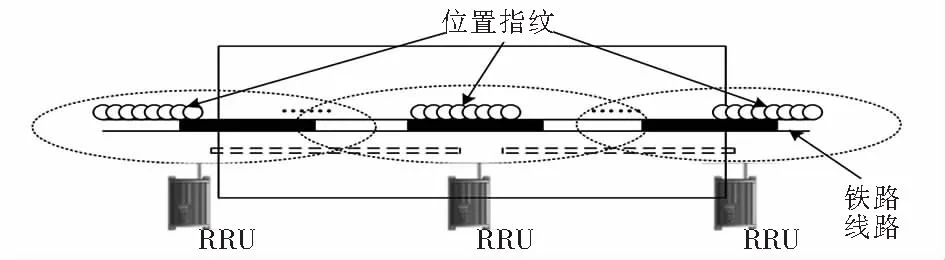
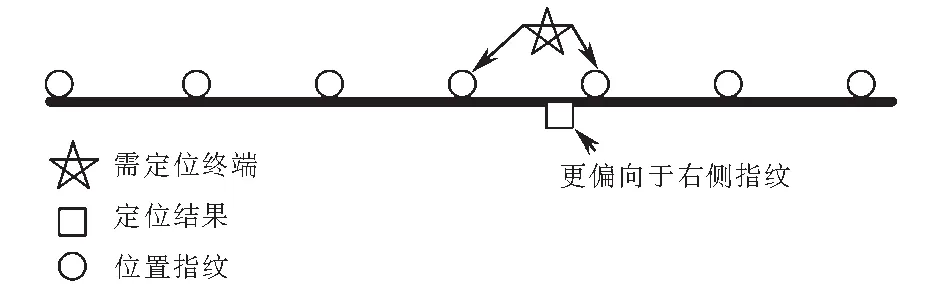
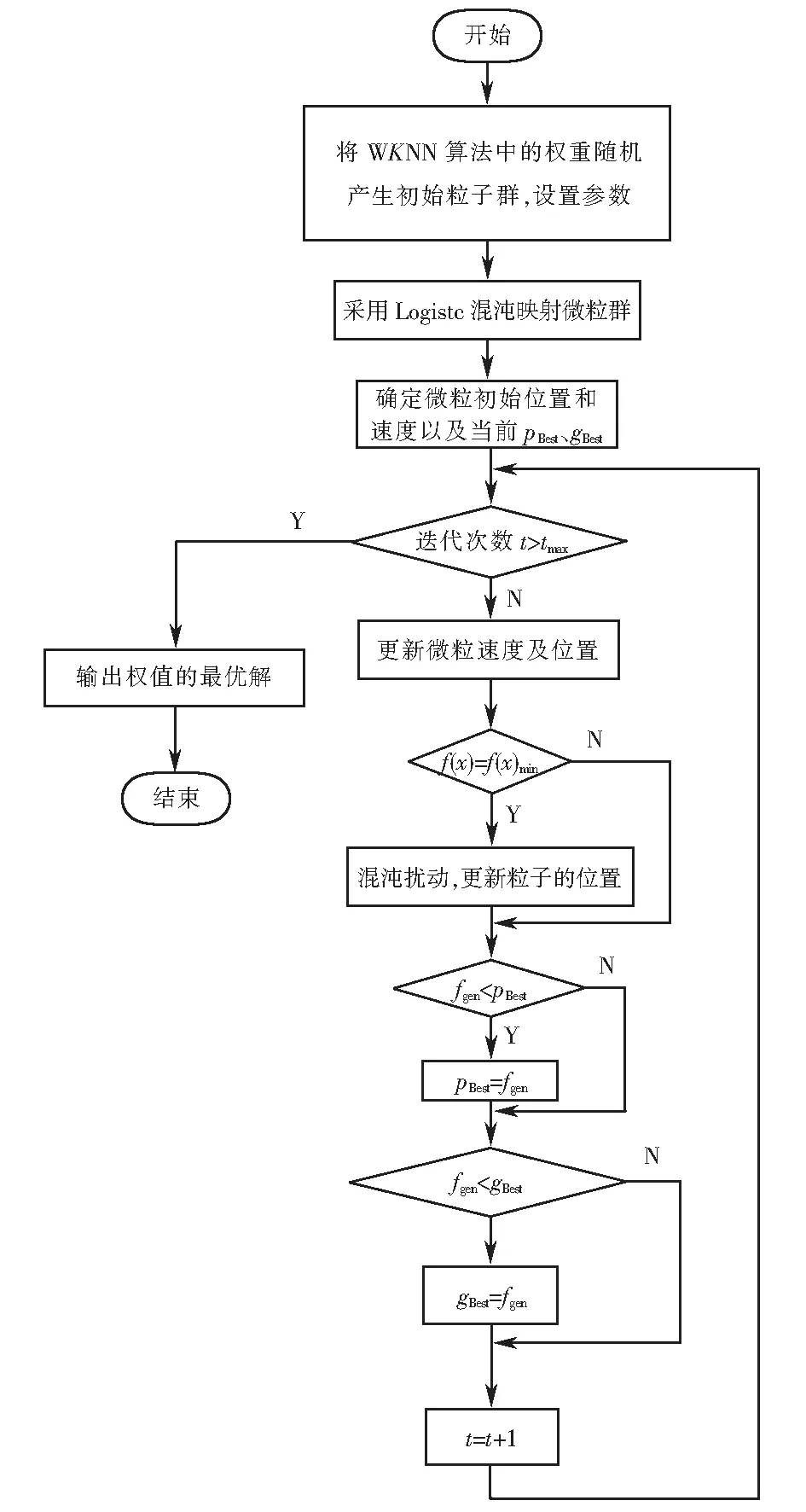
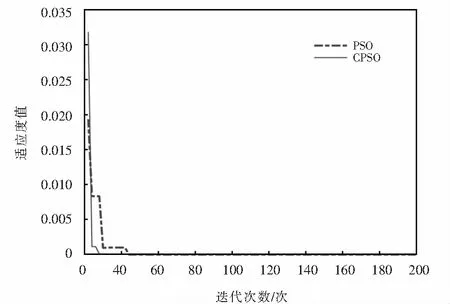
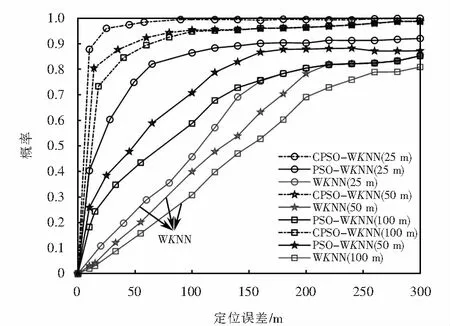
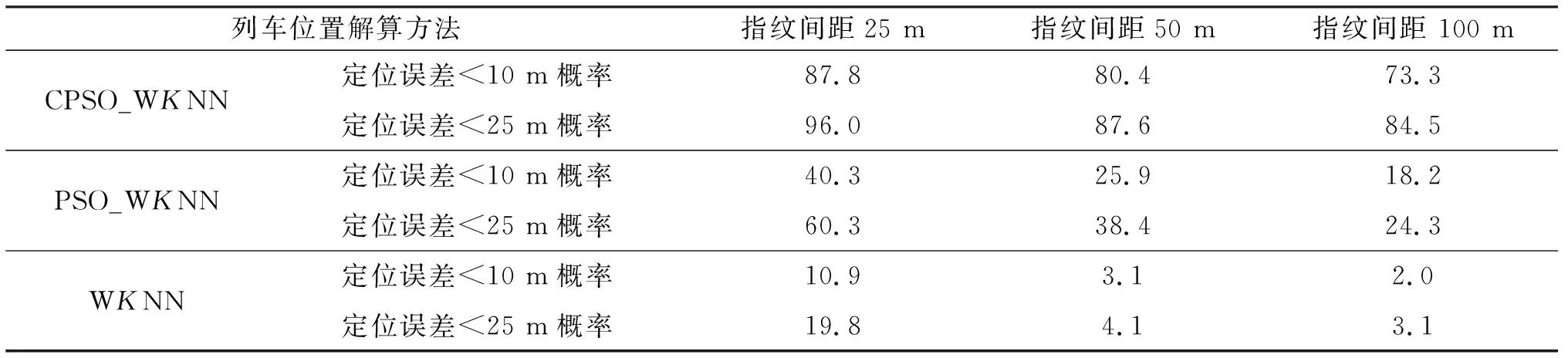
宽度修正因子L3取值：L3=alg(d′/2)，其中：0

改进的SPM损耗模型为：

L(d)=

(2)

2.2 列车位置指纹定位场景搭建

指纹定位的仿真场景如图2所示，实测隧道区域长度为20 km，基站天线增益为18 dBi，列车上的天线增益取值为0 dBi，铁路线路沿线的圆圈表示位置指纹定位离线阶段的采集点，采用式(2)作为LTE-R在隧道环境下的信道传输模型，在隧道区域内的任意采集点处的信号接收功率可通过式(3)计算.

Pr=Pt+APpower+FPpower-L(d)-σ,

(3)

图2 隧道环境下LTE-R列车位置指纹定位仿真场景Fig.2 Simulation scene of LTE-R train position fingerprint location in tunnel environment

其中：Pr为所求的接收信号强度；Pt为基站发射信号强度，设置为43 dBm；APpower为基站天线增益；FPpower为移动台天线增益；L(d)为信道传播模型中的路径损耗值；σ为高斯噪声，均值为0，隧道环境中标准差为6.

3 基于CPSO_WKNN位置指纹列车定位算法

3.1 离线阶段

离线阶段主要是在待定位的路径内设置一定量的采样点，通过轨道电路占用来获取待定位区间内不同参考位置的坐标，并通过本文建立的信道模型计算出各个采集点接收到的来自其周围AP的RSS值，将这些RSS值与采集点的位置坐标结合组成位置指纹条，并建立指纹数据库.位置指纹的间距选取会直接影响列车的定位精确度，因此本文分别设置了25 m、50 m、100 m三种间距进行采样，建立相应的位置指纹数据库.

3.2 在线阶段

1) 标准WKNN算法

在线定位阶段主要将实时测量得到的RSS值与数据库中的位置指纹数据进行对比，计算两者之间的距离，选取距离最小时的指纹条对应坐标位置作为估计位置，接收信号强度矢量RSS与数据库中各矢量之间的距离Dri通过式(4)计算[11].

(4)

其中：ssi为当前测试的第i条指纹对应的RSS矢量；Sij是寻找到的数据库中的指纹i到基站j的RSS矢量；当r=1时Dri为曼哈顿距离，当r=2时Dri为欧几里德距离.

接着采用WKNN算法对列车位置进行估算，首先选取了k(k≥2)个最接近的目标指纹的数据库矢量后，在每个数据库矢量对应的坐标上乘上了一个加权系数作为估计位置[12-13]，目标列车的位置估算如式(5)所示.其定位估算原理图如图3所示.

(5)

其中：(xi,yi)为指纹数据库中第i条指纹所对应的的坐标；ε为一个很小的正实数.

图3 WKNN定位原理示意图Fig.3 Schematic diagram of WKNN positioning

标准的WKNN算法主要是依靠距离的计算来估算目标点位置的，距离的计算精度是反映各个信号AP点信号强度矢量之间差异的关键，理想情况下物理位置越靠近的点，RSS之间的矢量差越小，定位精度越高.然而，物理距离的远近不是决定信号强度的差值大小的唯一因素，信号强度自身的波动很容易造成接收信号强度矢量RSS与数据库中各矢量之间的距离Dri不能真实的反映实际的物理位置差异，因此本文采用CPSO算法首先来优化WKNN算法中选取的权值，再对目标列车的位置点进行估算，从而提高最终的定位精度.

2) CPSO_WKNN位置指纹定位算法

CPSO算法就是将每个WKNN的权值看作一个粒子，在N维搜索空间中这些粒子按照一定的速度飞行，然后再将这些粒子从混沌空间映射到解空间，让其中少数粒子的飞行速度具有遍历性和随机性等特性，经过混沌化之后，这些粒子避免了PSO(particle swarm optimization)算法中容易陷入局部最优的缺点，使得在粒子群的演进过程中粒子不会过早收敛，最终搜索到粒子的全局最优值[14].在粒子群的进化过程中，还需要存储每一个粒子的最优位置和粒子群中所有粒子的最优位置，单个的粒子要与粒子群的最优位置进行比较，然后将粒子移动到粒子群的全局最优点，从而可以得到WKNN权值的最优解.

将初始粒子群混沌化时，采用Logistic模型产生混沌变量，如式(6)所示[15].

Xn+1=L(μ,Xn)=μXn(1-Xn),

(6)

其中:n∈N;Xn∈[0,1]；μ∈[0,4]为控制参数，当μ=4且Xn不等于0.25、0.5、0.75时Logistic映射是混沌不变集.

本文采用带有惯性因子的改进微粒群算法，可由式(7)～(8)表示[15].

v(i+1),j=ωvi,j+c1rand()(pBest-xi,j)+c2rand()

(gBest-xi,j),

(7)

x(i+1),j=xi,j+v(i+1),j.

(8)

其中:i代表第i个粒子；j代表粒子的第j维；pBest代表第i个粒子在进化过程中的最优位置；gBest代表粒子群中所有粒子所经历的最优位置；c1、c2为粒子的自学习因子和粒子群的学习因子，取值范围为0～2；rand()为(0,1)中的随机数；ω为惯性权重，若需要算法具有好的全局收敛能力，则ω取较大值，若需要算法具有好的局部收敛能力，则ω取较小值，实际取值时可采用线性递减法调整权重因子，以提高算法的优化能力，如式(9)所示.

(9)

其中：t代表第t代粒子；tmax为迭代的最大次数；ω∈[ωmin,ωmax]，根据专家经验ωmin取0.4，ωmax取0.9.

采用CPSO_WKNN位置指纹定位算法解算列车位置时，实际上可以看成寻找最小的权值使目标列车位置能够在指纹数据库中找到最接近其的位置坐标.因此本文以式(4)为基础，选取CPSO算法优化WKNN时的适应函数fitness(f)，如式(10)所示.

fitness(f)=

(10)

CPSO_WKNN位置指纹列车定位的算法流程图如图4所示.

图4 CPSO_WKNN位置指纹列车定位的算法流程图Fig.4 CPSO_WKNN location fingerprint train positioning algorithm flow chart

4 实验仿真及结果分析

为了检验经CPSO优化的WKNN位置指纹定位算法的优越性，本文以实际线路数据为依托进行仿真验证，测试线路长度 K208～K226，共设14个LTE-R基站，平均间距为1.3 km，最大指纹点为720个，每个指纹采集20个信号强度值存入离线阶段指纹数据库中，本文比较了单一的WKNN算法和CPSO_WKNN算法在指纹间距分别为25 m、50 m、100 m时的定位精确度,其中高斯噪声标准差取6，LTE-R仿真参数设置如表1所列.

采用CPSO对WKNN的权值进行优化时，参数设置为：初始粒子数为50个，混沌映射迭代次数为N.粒子群进化迭代次数取200次，经过对CPSO算法的仿真测试，取其实验最优结果确定惯性权重ω，取值从0.8到0.6线性递减取值，学习因子c1=c2=2，优化WKNN权值时，按式(10)计算适应度值，当其值小于0.000 1时算法结束.图5分别为采用CPSO和PSO算法优化WKNN权值的适应度变化曲线.

从图5中可以看出，CPSO算法优化WKNN权值时收敛速度更快、效果更好，在迭代了9次时，算法已得到很好的收敛，适应度值已小于0.000 1，而PSO算法优化WKNN权值时，迭代至23次时才得到很好的收敛.为了验证CPSO优化的WKNN位置指纹定位算法的定位精确度，分别采用CPSO_WKNN、PSO_WKNN以及WKNN算法分别在指纹间距为25 m、50 m、100 m时进行定位.图6为三种方式解算列车位置的精确度结果比较.从图6中可以看出，采用CPSO_WKNN、PSO_WKNN以及WKNN分别对列车进行位置指纹定位时，定位的误差均随指纹间距的增大而增大，采用优化算法对WKNN的权值进行优化后，定位误差明显减小，且可以看出CPSO_WKNN位置指纹定位的精度明显高于PSO_WKNN位置指纹定位的结果，验证了CPSO算法对于WKNN算法的定位结果具有良好的修正作用.

表1 LTE-R仿真参数Tab.1 LTE-R simulation parameters

图5 适应度变化曲线Fig.5 Fitness curve

图6 CPSO_WKNN、PSO_WKNN、WKNN位置指纹列车定位误差Fig.6 CPSO_WKNN、PSO_WKNN、WKNN position fingerprint train positioning error

表2给出了三种不同位置解算方式下的指纹间距分别取25 m、50 m、100 m时的定位结果，结合图6可以看出：当指纹间距为25 m时，CPSO_WKNN位置指纹定位方式下有87.8%的概率定位误差小于10 m，有96%的概率定位误差小于25 m；而PSO_WKNN位置指纹定位方式下定位误差小于10 m的概率仅40.3%，WKNN位置指纹定位定位误差小于10 m的概率仅10.9%；当指纹间距分别为50 m和100 m时，CPSO_WKNN位置指纹定位方式下定位误差小于10 m和定位误差小于25 m的概率都明显高于PSO_WKNN及WKNN的位置指纹定位.结合实际现场考虑，基于LTE-R网络下若采用CPSO_WKNN位置指纹定位，可选取25 m指纹采集间距，在该情况下定位误差超过87%概率小于10 m，可以满足列车的高精度定位.

表2 CPSO_WKNN、PSO_WKNN、WKNN位置指纹列车定位结果Tab.2 CPSO_WKNN、 PSO_WKNN、WKNN location fingerprint train positioning results %

5 结论

本文在以LTE-R信号特征强度值作为WKNN位置指纹定位列车的基础上，引入CPSO优化算法对WKNN的权值进行寻优操作，采用CPSO_WKNN位置指纹定位算法对列车位置坐标进行解算.实验验证结果表明：单一的WKNN位置指纹定位精度很低，当指纹间距为25 m时，其定位误差小于10 m的概率仅为10.9%；若采用PSO算法优化WKNN的权值后，由于PSO算法容易陷入早熟，虽可将该条件下的概率值提高到40.3%，但仍不能满足列车高精度的定位需求；本文提出的CPSO_WKNN位置指纹定位算法成功的将指纹间距取25 m时列车位置误差小于10 m的概率提高至87.8%，且通过验证证明CPSO优化WKNN权值时比PSO算法更快收敛，在第十一步时就可以收敛到最佳状态，因此CPSO_WKNN位置指纹定位算法可以满足列车的高精度实时定位.因为本文是基于LTE-R的信号强度特征值进行位置指纹定位，能够充分的利用已有设备完成高铁隧道环境下GPS/BDS定位盲区中列车的高精度定位问题，也为扩展LTE-的应用提供了可能.