低效课堂“变形升级记”

樊曦

[摘 要]课堂低效是困扰教师的一个普遍问题。“多边形的内角和”这节课内容多，教学任务重，需让学生抓住已知的三角形的内角和，进行从简单到复杂的有序思考，通过合情推理、演绎推理，逐步探究多边形的内角和，使课堂更加紧凑高效，将低效课堂“变形升级”。

[关键词]课堂;变形升级;多边形的内角和

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）29-0074-02

一、確定已知，唤醒已有经验

【复习三角形的内角和，引出多边形的内角和】

一般探究多边形的内角和的教学方式是先确定学生已过的知识：（1）多边形概念;（2）内角和的概念。根据以上两点进行初步设计：（1）展示三角形，并让学生说一说什么是三角形的内角、三角形的内角有什么特点、如何判断三角形内角和;（2）再出示四边形、五边形、六边形、七边形……引出多边形的概念;（3）最后推出“探究多边形的内角和”课题。

以上冗杂、琐碎的引入环节可以“变形升级”。

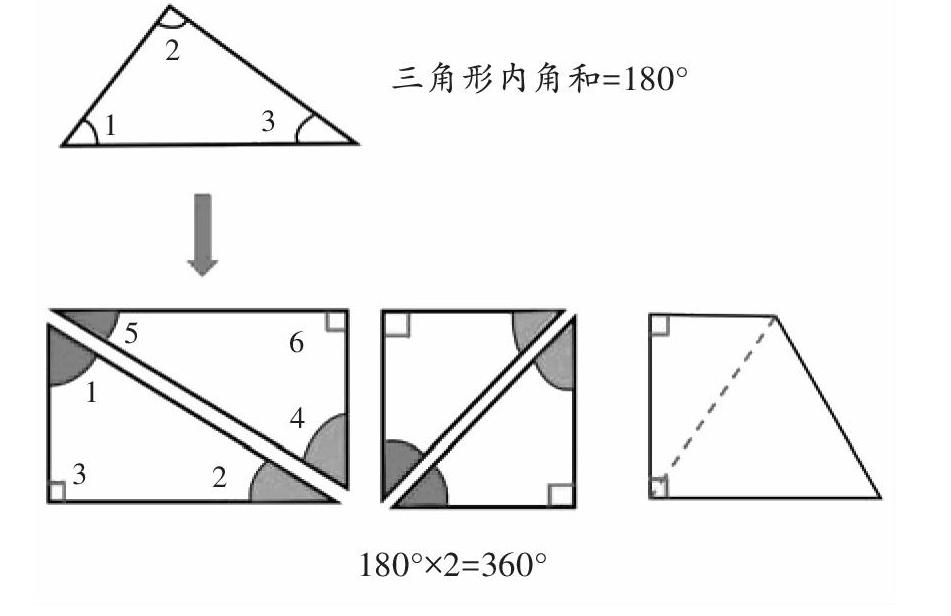
（教师出示一个三角形，并标出其中一个内角∠1）

师：这是三角形的一个内角∠1，谁还能找出这个三角形的其他内角？

（学生指出内角∠2、内角∠3）

师：三角形的这三个内角有什么关系？

生1：∠1+∠2+∠3=180°，三角形的内角和是180°。

（教师出示四边形、五边形、六边形、七边形……）

师：其实这些图形都有一个共同的名字。

生2：多边形。

师：没错。多边形与我们学习过的三角形一样，都有内角和，今天我们就一起来探究“多边形的内角和”。（板书课题）

【思考】

课堂的引入环节应简洁紧凑，并准确串联旧知识和新知识。“变形升级”后的教学删除原先“东一榔头西一棒”的冗杂无用的复习环节，扣住三角形的内角和，从三角形的内角和过渡到多边形的内角和，这样删繁就简的“改造”让课堂教学更加明晰。

二、更新旧知，建立准确联结

【利用三角形的内角和探究四边形的内角和】

根据简单到复杂的探究规律，下一步应探究四边形的内角和。原先的教学设计如下：让学生拿出准备好的四边形纸片，并用不同的方法探究四边形的内角和。但是，用多种方法尝试探究多边形的内角和不应是本节课的重点。

重点应是在三角形的内角和与多边形的内角和之间建立紧密联系，三角形内角和这一重要知识必须贯穿教学的始终，使学生感悟从特殊到一般、从简单到复杂、从合情推理到演绎推理的数学探究过程。

师：你们知道长方形的内角和是多少吗？

生1：长方形的四个角是直角，所以长方形的内角和是90°×4=360°。

师：是的，那你们能用三角形内角和的知识解释长方形的内角和是360°的原因吗？

生2：可以把长方形分成两个三角形，一个三角形的内角和是180°，长方形的内角和就是两个180°，即360°。

师：那正方形的内角和是多少呢？

生3：正方形的四个角是直角，它的内角和是90°×4=360°。

生4：正方形也可以分成两个三角形，它的内角和也是两个180°，即360°。

师：直角梯形的内角和是多少？

生5：直角梯形也可以分成两个三角形，内角和也是两个180°，即360°。

师：我们用已有的知识解决了这个问题，还有其他验证方法吗？

生6：用量角器量出梯形的四个角度数，再求和。

师：四个角都需要量吗？

生7：不需要，直角梯形有两个直角，只用量剩下两个角。

（学生量角，并计算90°×2+60°+120°=360°，梯形的内角和是360°）

师： 长方形、正方形、直角梯形都是四边形，这些四边形的内角和都是360°。

生8：四边形都能分成两个三角形，所以四边形的内角和=180°×2=360°。

【思考】

“变形升级”后的教学去掉了原本低效的活动，确定探究活动的主线“多边形的内角和”，学生在探究中初步发现探究多边形的内角和的方法就是利用三角形的内角和知识，体会三角形的内角和与多边形的内角和之间的联系。课堂教学目标逐渐清晰，教师轻松教，学生轻松学。

三、挖掘新知，掌握自学方法

【探究五边形的内角和，掌握方法】

师：你们想继续探究什么图形的内角和？

生1：五边形。（从简单图形开始，四边形后就是五边形，有序研究，板书：简单、有序）

师：想用什么方法探究？

生2：分割的方法。

师：将五边形分成三角形，也就是利用我们学过的三角形内角和的知识。

（教师出示五边形，学生自主探究五边形的内角和，展示不同的分法）

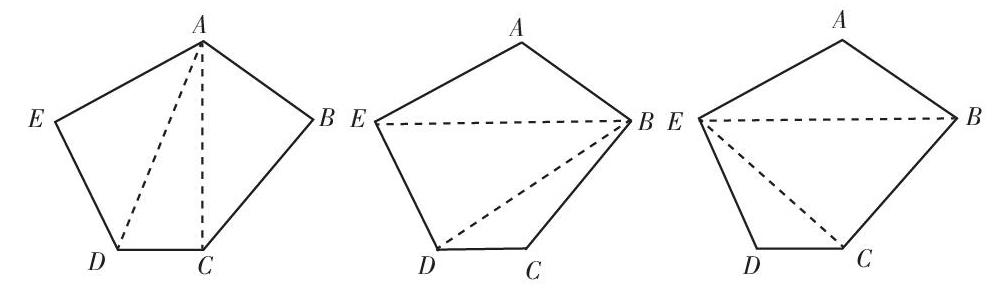
生3：从A点出发，分别与C点和D点连接，把五边形分成3个三角形，五边形的内角和等于180°×3=540°。

生4：也可以从B点出发，分别与D点和E点连接，也能分成3个三角形，五边形的内角和等于180°×3=540°。

生5：还可以从E点出发，分别与B点和C点连接，也是把五边形分成3个三角形。

师：他们的分法都有什么共同点？

生6：都是从同一个顶点出发，连接与该点不相邻的其他顶点，将五边形分成3个三角形。

利用三角形的内角和探究了四边形的内角和后，再探究五边形的内角和是帮助学生掌握用分三角形的方法探究多边形内角和的重要过程。不过，在分割多边形的过程中，如果分割方法错误会导致分割出多余图形。

【特殊错误案例】

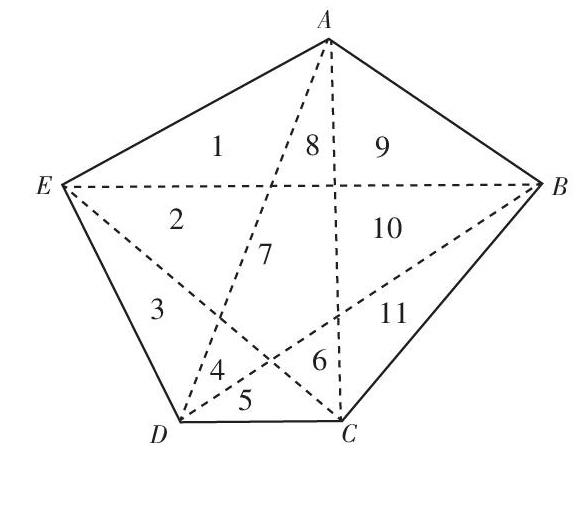
生7：我分出了10个三角形，还有一个五边形！（如下图所示）

师：这位同学分得对吗？

生8：他分得不对，我们要算的是内角和，他分出图形中的很多角不是五边形的内角。

师：是的。

【思考】

教师引导学生发现，上图1、2、3这几个部分组成了一个三角形，4、5、6、7、8这几个部分组成了一个三角形，9、10、11这几个部分组成了一个三角形。虽然分成了11个部分，其实还是3个三角形。在这3个三角形里再分图形是没有必要的。教师要结合教学实际情况，帮助学生掌握分割图形的正确方法。

四、探索未知，交流满满收获

【自主探究，交流收获】

教师是学生学习上的引导者，完整的教学也少不了学生的自主探索和积极思考。学生在经历四边形的内角和、五边形的内角和的探究后，再自主探究其他多边形的内角和，然后在交流中先发现多边形的内角和与分成的三角形的个数有关，再发现分成的三角形的个数又和多边形的边数有关，讨论多边形边数、分成的三角形的个数、内角和之间的关系，并在黑板上书写展示。学生带着从简单到复杂、从特殊到一般的数学探究思想一步步推理，自然得出“多边形的内角和=（边数-2）×180°”的结论，最后再验证这个结论。把课堂时间留给学生，精彩的课堂一气呵成。

【思考】

本节课的教学应达到三个效果：（1）学生明确多边形的内角和是根据三角形的内角和推算出来的;（2）在探究过程中，学生体会从简单到复杂的有序思考是探究规律的有效方法;（3）学生学会当再遇到新的问题时，可以把新问题转化成能用已有知识解决的问题。教师应该勤思考、多实践，让自己的每一节课都能“变形升级”，逐渐高效。

（责编 黄 露）