基于一道物理竞赛题海市蜃楼现象演示及理论分析
2021-11-04陈文娟
潘 刚 方 莲 陈文娟
(合肥工业大学基础部,安徽 合肥 242000)
1 引例问题
在参考文献[1]中有这样一道中学物理竞赛考题:
问题.已知飞机场跑道上空空气的折射率随高度变化的规律是n=n0(12+αy),其中α=1.5×10-6,n0是地面处空气的折射率,某人站在机场跑道上看远处,他的眼睛距离地面的高度是h=1.7 m,求他能看到跑道的长度.
这道题目显然是一个变折射率光学问题.观察空气折射率随高度变化的关系式可知,空气越往上折射率越大,根据折射定律(图1),光线水平入射必向上弯曲射入人眼.那么逆着光线看,光线水平入射的点是此人能观察到的最远的点.所以需要关注光线的弯曲情况,建立光线满足的微分方程.这是本考题的核心和关键点.
光学中可以由费马原理导出折射定律

图1 折射定律

式中角度θ为光线方向与法线的夹角.
用微元法考察曲线(图2)则有

图2 利用微元方法考察曲线
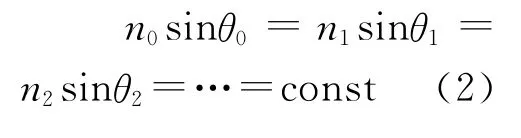

图3 光线方程满足的守恒量

联立(2)、(3)两式得到
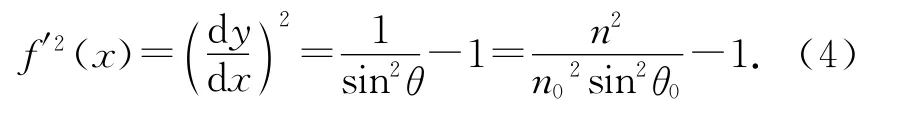
方程(4)便是光线的微分方程表达式.代入求解

因为α=1.5×10-6≪1,略去α的高次项得到

分离变量法得到

代初值条件y(0)=0得到

这就是求出的光线方程表达式f(x),当y=1.7时算得x=1505.55,这就是人站在跑道上能看到的最远距离.
基金项目:本文系安徽省省级线上教学优秀课堂大学物理项目(项目编号:2020xskt388)阶段研究成果之一.
通过引例问题可以看出,本题中给出了折射率梯度,要求计算光线方程并分析一些问题.那么对于要研究的海市蜃楼问题,可以采用类似的方法.不过这个问题中折射率梯度具体是什么,还需要结合其他的物理知识进行计算.
2 实验设计及理论计算
2.1 海市蜃楼模拟装置介绍
现实大气环境中的那样,制造出一个有折射率梯度的气体流体,则无论是构造压强梯度还是温度梯度都是十分困难的.而由于光线在具有折射率梯度的液体流体中传播时也会发生弯曲现象,所以可以利用液体来实现海市蜃楼现象的模拟.图4,图5是笔者根据参考文献[2-7]提供的思路搭建的实验室条件下模拟海市蜃楼的装置,该装置可以在3 min以内模拟出海市蜃楼现象,非常适用于物理课程教学时的实验演示.

图4 海市蜃楼现象演示器材(实物图)

图5 海市蜃楼现象演示器材(结构图)
实验前需要在配液桶1中装有足够的清水,观景槽7和混合槽3里都装上浓度为M,体积为V的饱和食盐水.实验开始时,打开抽水泵和可调速阀门,通过保持混合槽满水使淡水注入的流量等于混合槽盐水流出的流量Q,混合槽内的溶液体积将保持为V不变,而溶液浓度却随时间改变.对于食盐水来说,浓度变化就决定着折射率的变化.变化浓度的食盐水从混合槽3流入注液浮槽6中,表现为注液浮槽6中不同高度的盐水层有不同的浓度,这就形成了折射率梯度.这样把物体放在后面就可以观察到光线弯曲所形成的像.
关于折射率梯度的计算方法,可以认为在注入液体的过程中,溶液不发生扩散.但在实际操作过程中溶液具有均一性,最后的浓度分布必将趋于一致.因此实验中要注意演示用的溶液需现用现配,更不要在实验中大幅度的晃动溶液.
如果已知装置的技术参数,可以计算光线的弯曲偏移量.装置的主要技术参数如表1.

表1 装置的主要技术参数
常温下食盐的溶解度为36 g,则饱和食盐水的质量分数为

至于食盐水浓度与折射率的关系,可以通过实验进行测定.测量液体折射率的方法多种多样,也可以引用参考文献[8]的测量数据(见表2)进行拟合.

表2 食盐水浓度与折射率关系测定(原始数据)
用Excel线性拟合表达式为

图像如图6所示.
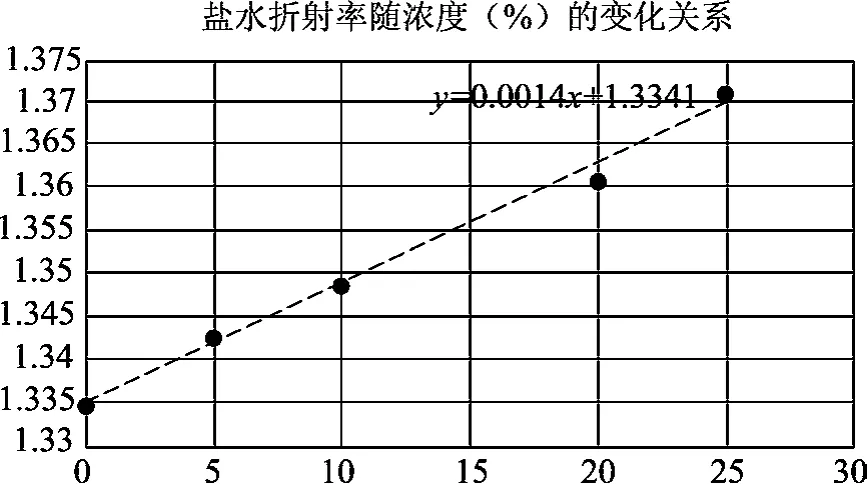
图6 食盐水折射率与浓度的Excel拟合图
2.2 海市蜃楼现象定量计算
首先来观察单束光线的偏移,通过计算浓度变化得到折射率分布,再用前面的方法计算光线方程得到偏移量.设食盐水浓度ω%,则有微分方程

积分并代入有关参数得到(初始饱和食盐水质量分数ω0%=26.47%)

对于注液浮槽6,有注入盐水的高度

利用(5)式反解出t,并联立(10)、(12)式得到盐水折射率随高度h的变化

为了简化计算,这里利用e指数函数的一阶展开式ex≈1+x把(14)式改成线性变化的,这样就可以直接套用前面引例问题的结论.

线性变化的介质光线弯曲呈一条抛物线,它的光线方程前已计算为(8)式,这里,光线沿注水浮槽长边入射,x=33.6 cm.数值计算得到

与实验多次测量的平均值Δy0=-5.58 cm基本吻合.图7实验装置中光线的弯曲情况.

图7 对水平入射光线的偏移量观察
图8-11是海市蜃楼现象的演示照片.明显可见,装置演示了上现蜃景,呈现正立的像,所成像比原物体略暗.

图8 原物体

图9 实验开始前加遮挡板

图10 配液过程(已加遮挡板8)

图11 实验结束后观察到的上现蜃景
3 总结与展望
海市蜃楼现象是一个变折射率光学问题.本文首先建立折射率随高度变化模型,然后建立光线的微分方程(4)式模型,并给出一组具体数值进行讨论.在实验中,笔者设计了一套模拟海市蜃楼现象的装置.这套装置可以在3 min内演示出海市蜃楼现象,极大提高了演示的效率.所观察到的光线弯曲现象也与理论计算值相吻合.总的来说,笔者所建立的物理模型是比较通俗易懂的,微分方程(4)式始终贯穿于全文,对于折射率仅在一个方向上变化的介质可以很好的应用.设计的实验装置也能验证理论模型的思想.但是,对于真实大气环境的模拟以及下现蜃景的模拟还存在技术上的难关,这可以作为下一步的研究方向.
