巧妙求解均匀带电残缺球面球心处的电场强度——“气体对半球面压力的计算方法”的迁移应用

俞 翔

（江苏省阜宁中学，江苏 盐城 224400）

关于均匀带电的残缺球面球心处的电场强度，文献中一般应用圆环带法、场强叠加原理及球坐标法、端面积分法、电势梯度法等求解.相比较而言，端面积分法和电势梯度法是比较简单的方法，计算过程相对简洁，而圆环带积分法和电场强度叠加原理及球坐标法计算繁杂，这些方法大多数中学生均难以理解和掌握.本文通过模型构建，给出巧妙计算均匀带电的残缺球面球心处电场强度的几种初等方法，以供参考.

1 气体对半球面压力的计算方法

例1.如图1所示，半径为R的半球形封闭容器内充满压强为p的气体（重力忽略不计），求气体对半球面的压力.

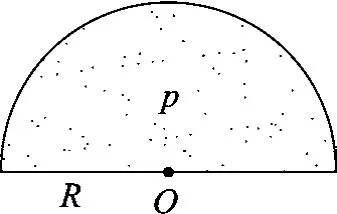
图1 气体充满半球形容器

分析：直接计算气体对半球面的压力，一般要用微元法叠加求积分，才能得出结果.若应用转化的思想方法，可通过求解气体对底部圆面的压力，也很容易得出了气体对半球面的压力.

解析：以半球形容器内的气体为研究对象，底部圆面对气体有向上的支持力F1，半球面对气体有向下的压力F2.对半球形容器内的气体有平衡条件有F2=F1.根据牛顿第三定律，气体对底部圆面的压力等于F1，而气体对半球面的压力方向向上，其大小F=F2=F1=pπR2.

2 均匀带电残缺球面球心处电场强度的分析与计算

如图2所示，半径为R的残缺球面均匀带电，电荷面密度为σ.求球心O点的电场强度.

图2 均匀带电的残缺球面

2.1 均匀带电残缺球面球心处电场强度方向的分析

图3 场强方向的分析

2.2 均匀带电残缺球面球心处电场强度大小的计算

均匀带电残缺球面球心处电场强度大小的计算，一般采用积分和偏微分计算，对中学生而言数学要求过高.

笔者研究发现，若把气体对半球面压力的计算方法，迁移到这个问题的求解之中，也可十分顺利地用初等方法解决该问题.

（1）试探电荷对球面的作用力产生的压强.

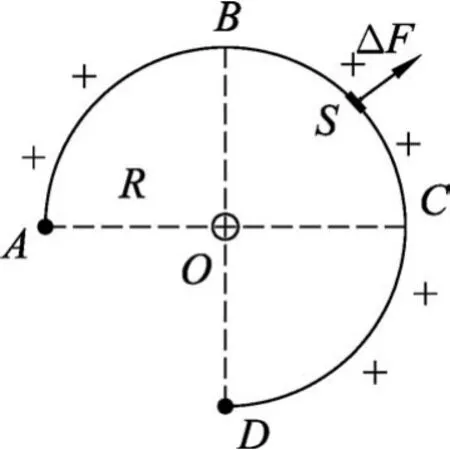
图4 试探电荷对面元的作用

所以，半球面单位面积上受的库仑力是定值，即压强为

可见，求残缺球面上所有小面元所受试探电荷的库仑力之和，就转化成了求压强对残缺球面的压力之和.这样，可引导学生构建气体的封闭容器模型，迁移学生已经熟练掌握的气体对半球面压力的计算方法，实现对所求问题的巧妙转化.

（2）构建多种气体的封闭容器模型，计算残缺球面球心处场强的大小.

构建模型（1）：以半径为R的球面与半径为R的水平半圆AO、竖直半圆DO3部分构成一个封闭容器，如图5所示.容器内部充满压强为的气体，则气体对球面的压力的矢量和F（图中未画出），与气体对水平半圆AO向下的压力FAO和竖直半圆形DO向左的压力FDO的合力等值反向.则

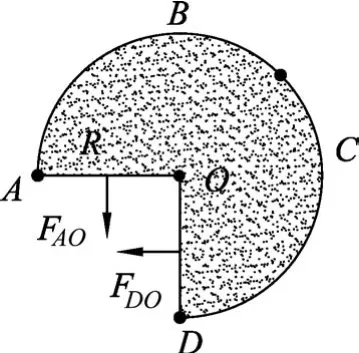
图5 间接计算球面的受力

构建模型（2）：以半径为R的球面BC与半径为R的竖直半圆BO、水平半圆CO3部分构成一个封闭容器，如图6所示.容器内部充满压强为的气体，则气体对球面BC的作用力的大小，等于竖直半圆BO所受的向左的压力FBO和水平半圆CO所受的向下的压力FCO的矢量和，同理可以得到与模型（1）相同的结果.

图6 间接计算球面BC的受力

说明：学生构建封闭容器模型时，容易在图5中以AD为直径构建一个圆面（其实此圆面与球面ABCD不能构成封闭容器），或者在图6中以BC为直径构建一个圆面（此圆面与球面BC不能构成封闭容器），得出的结果与上述模型得出的结果不一致.这时，教师通过引导学生观察球面的立体模型，让学生自己发现其错误，并纠正错误.

构建模型（3）：以半径为R的半球面ABC和它的底面圆构成一个封闭容器，如图7所示.容器内部充满压强为的气体，则气体对半球面ABC的压力的矢量和，与气体对半球形容器底部圆面的压力等值反向，求气体对半球面的压力，可转化为求气体对底部圆面积πR2的压力，其大小为

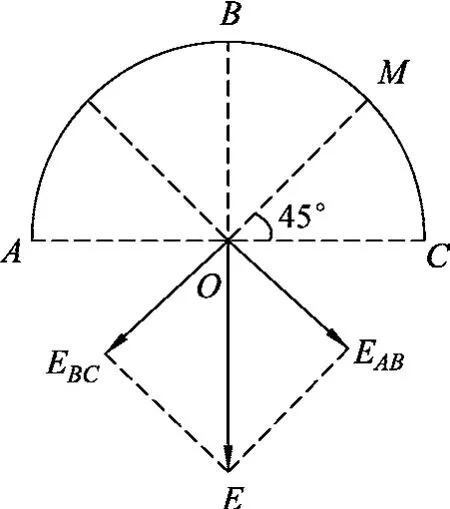
图7 场强合成图

根据牛顿第三定律和电场强度的定义式，半球面上的电荷在球心处产生的电场强度为

（9）式与（6）式的结果一致.