2021年全国高考广东物理卷问题情境特点及其分析策略

刘宇虹 邓治国

（1.广州市增城区郑中钧中学，广东 广州 511300；2.广州市增城区教师发展中心，广东 广州 511300）

高考评价体系中的“四层”考查内容和“四翼”考查要求，是通过情境与情境活动两类载体来实现的，即通过选取适宜的素材，再现学科理论产生的场景或是呈现现实中的问题情境，让学生在真实的背景下发挥核心价值的引领作用，运用必备知识和关键能力去解决实际问题，全面综合展现学科素养水平.[1]2021年全国高考广东物理卷紧跟《中国高考评价体系说明》的观点，呈现明显的问题情境特征.为更好发挥高考引导教学的功能，笔者以新高考问题情境为基础，通过对高考题多角度、深层次研究，提炼“一般解题思路”与“正反相推”、“异中求同”、“殊途同归”等几种特殊情境分析策略，以此为抓手促进教师、学生在问题情境中体验解题思路与物理思维方法，培养学生的物理核心素养.

1 高考广东物理卷问题情境特点与一般解题思路

2021年全国高考广东物理卷考题通过大量真实材料进行设计，紧扣我国科技发展、生活生产应用、国防事业、中华民族文化、防疫等方面，体现物理对生产生活、科学技术发展所产生的指导、应用、推动、创新等作用，笔者从主要知识点、情境来源、一般解题思路3个方面梳理，如表1所示.

表1 2021年全国高考广东物理卷题梳理

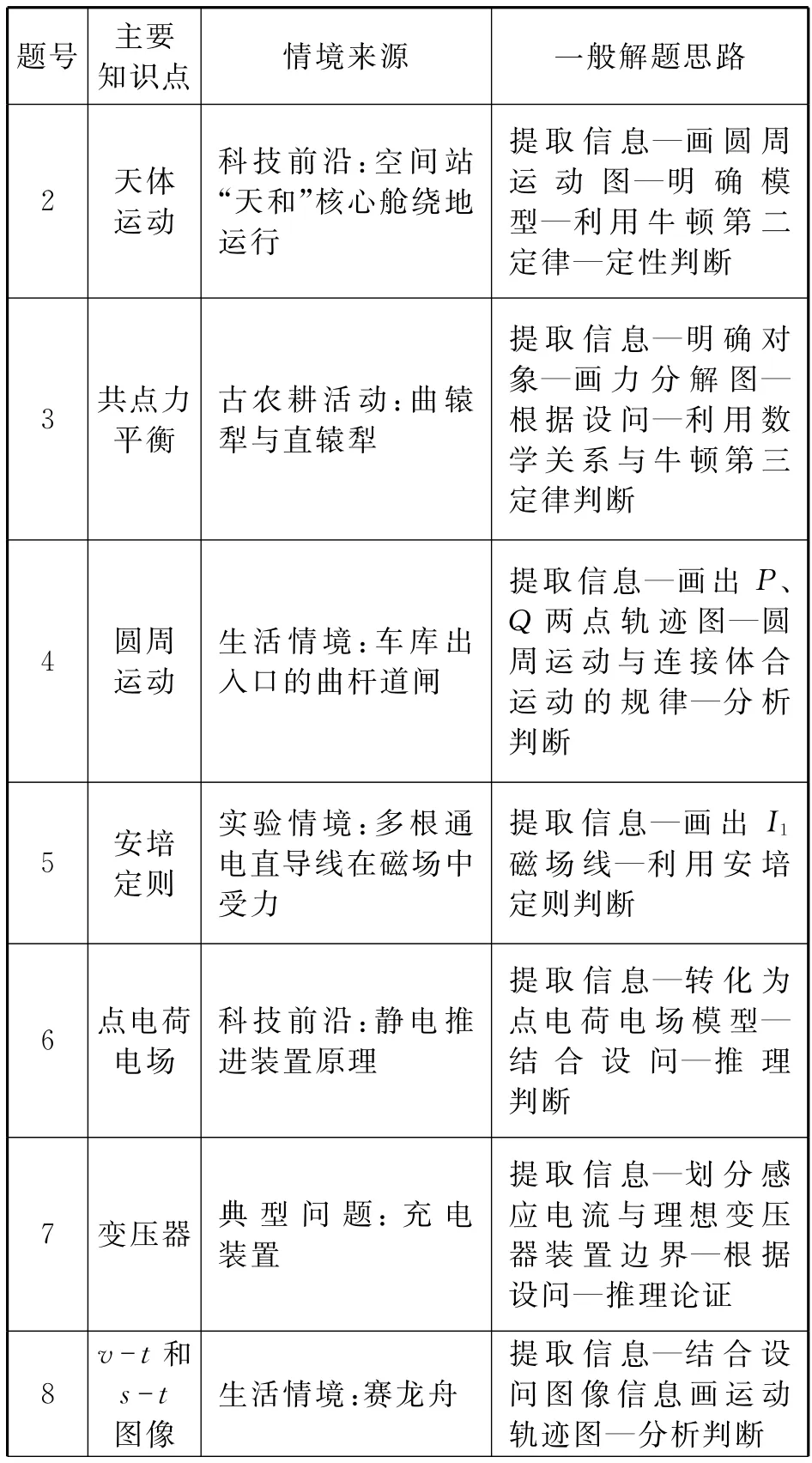
续表

续表

从高考问题情境特点来看，仅靠以前的“题海战术”、“反复多次相同讲解”、“只要多做多练就好”的教学难以在高考中赢得先机.因此，在物理试题讲评中，以什么方式改变上述现象，如何开展以培养学生的物理核心素养为目标的教学实践是应当思考的问题.如果说物理教学思路为“以物说理，以理格物”，那么物理试题则需要依托真实情境，巧设问题角度，考察学生用物理语言分析真实情境的能力，用基本概念、规律及其蕴涵模型分析情境的能力.从2021年全国高考广东物理卷考题具有明显引导教学功能，对规范师生解题思路具有指导作用.高考试题分析的基本过程为：首先是问题情境转化为物理图景（注重动手）、再者是物理图景转换成物理模型（注重动脑）、接着是结合概念规律分析适用条件与应用范围、最后利用数学等工具得出结论.

2 高考问题情境试题的特殊分析方法

在《普通高中物理课程标准》中提出，高中物理课程的目标是要求学生经过学习之后，具有理想信念和社会责任感，具有科学文化素养和终身学习的能力，具有自主发展能力和沟通合作能力.[2]因此，物理解题需开展多角度、深层次的教学策略，以培养学生的物理核心素养为目标，促进学生分析问题和解决问题的能力的提升，既关注学生的情感培育、人文素养和情怀生成，又关注学生的思维提升、能力形成、思想感悟.

2.1 选择题情境分析：正反相推

例1.（2021年广东高考物理第2题）2021年4月，我国自主研发的空间站“天和”核心舱成功发射并入轨运行，若核心舱绕地球的运行可视为匀速圆周运动，已知引力常量，由下列物理量能计算出地球质量的是

（A）核心舱的质量和绕地半径.

（B）核心舱的质量和绕地周期.

（C）核心舱的绕地角速度和绕地周期.

（D）核心舱的绕地线速度和绕地半径.

该题以我国今年航天航空事业的热点——“天和”核心舱成功发射为情境，设计了计算地球质量的问题，将国家航天科技的重大发展与万有引力定律、圆周运动的基本知识相结合，学生在解题的同时了解大国航天重器的发展，渗透人文素养、民族自信和家国情怀.本题的解题策略如下.

首先，根据题干中提到“核心舱绕地球的运行可视为匀速圆周运动”，引导学生将真实情境进行转化，作出物理情境图1，调用匀速圆周运动的基本模型.

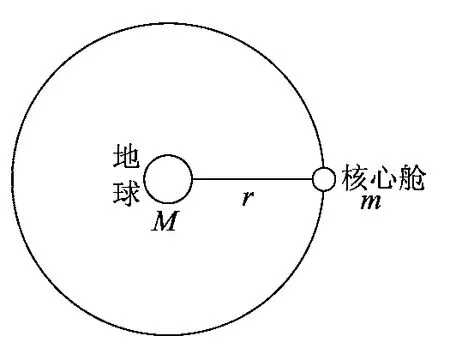
图1 核心舱绕地球运行物理情境图

其次，针对选择题的题干和选项都有一定已知条件的特点，教师设计正向推理和反向推理两个角度，促进学生分析问题和解决问题能力的提升.

设地球质量为M，核心舱质量为m，绕地半径为r，绕地周期为T，核心舱的绕地角速度为ω，核心舱的绕地线速度为v.

角度1：正向推理.

正向推理是指根据题干已知条件进行计算、判断或推理而得到选项答案.由该题题干可知，核心舱做匀速圆周运动，万有引力提供向心力.由此可得

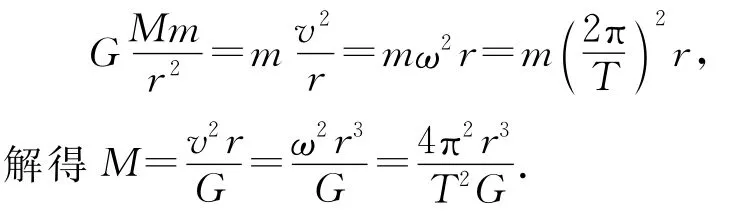
因此，需计算出地球质量，除万有引力常量G外，还需知道的物理量有核心舱的绕地线速度v和绕地半径r，或者核心舱的绕地角速度ω和绕地半径r，再或者绕地周期T和绕地半径r.故正确答案为（D）.

角度2：反向推理.

反向推理是根据题干和选项，将选项条件代入进行计算、判断或推理得出结果，若符合题干则得到正确选项.

通过正向推理及反向推理，让学生在解决问题中，懂得解决问题的不同方式.当面对一种角度难以解决新问题时，可尝试另一角度解决，提升学生解决问题的能力.

2.2 实验题情境分析：异中求同

例2.（2021年广东高考物理第11题）某兴趣小组测量一缓冲装置中弹簧的劲度系数，缓冲装置如图2所示，固定在斜面上的透明有机玻璃管与水平面夹角为30°，弹簧固定在有机玻璃管底端，实验过程如下：先沿管轴线方向固定一毫米刻度尺，再将单个质量为200 g的钢球（直径略小于玻璃管内径）逐个从管口滑进，每滑进一个钢球，待弹簧静止，记录管内钢球的个数n和弹簧上端对应的刻度尺示数Ln，数据如表2所示，实验过程中弹簧始终处于弹性限度内，采用逐差法计算弹簧压缩量，进而计算其劲度系数.

图2 缓冲装置

表2 测量数据

（1）利用ΔLi=Li+3-Li（i=1，2，3）计算弹簧的压缩量 ΔL1=6.03 cm，ΔL2=6.08 cm，ΔL3=______cm，压缩量的平均值________cm；_

（2）上述ΔL是管中增加________个钢球时产生的弹簧平均压缩量；

（3）忽略摩擦，重力加速度g取9.80 m／s2，该弹簧的劲度系数为________N／m（结果保留3位有效数字）.

该题是创新性实验题，源于教材又不拘泥于教材，主要考点为胡克定律与受力分析，在试题的情境设计上进行了创新，改变了教材弹簧的劲度系数实验的装置、方法和数据处理方式等，但物理知识“万变不离其宗”，考核了不同实验情境下迁移和变通实验知识的能力.

解题的难点在于理清新实验的原理，这要求学生需要一定的科学探究能力和思维变通能力，善于改变原有的实验方式，运用题目给出的新思路进行分析，着力寻求与常规实验相似的原理和方法，“异中求同”地进行问题的解决，如图3.该题的解题策略如下.

图3 “异中求同”的思维过程

（1）异中求同.

寻求与常规实验相似的原理展开思考.题干“测量一缓冲装置中弹簧的劲度系数”表明了实验的目的，比较试题实验与教材实验的相同之处后，学生可联想到实验蕴含的规律为F=kx，其中x为弹簧形变量.

（2）思维聚焦.

思考试题实验与教材实验的不同之处，发现是F与x的测量方式不同.以小球作为研究对象，在斜面上进行受力分析（如图4），构建受力平衡模型.设弹簧原长为L0，可得放置一个小球时F1=mgsin30°=kx1，x1=L1-L0；放置两个 小球时F2=2mgsin30°=kx2，x2=L2-L0；放置n个小球时Fn=nmgsin30°=kxn，xn=Ln-L0.

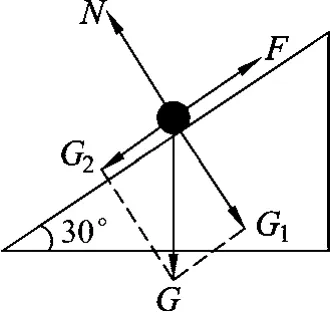
图4

根据题干“ΔLi=Li+3-Li（i=1，2，3）计算弹簧的压缩量”可联想到Δx=ΔLi，由相关弹簧规律ΔF=kΔx，即Fi+3-Fi=k（Li+3-Li）=3mgsinθ，由此理清实验原理，突破本题难点.

（3）问题解决.

问题（1）解决：根据题中“ΔLi=Li+3-Li”和逐差法提示，代入表格数据进行运算，可得

问题（2）解决：根据kΔLi=k（Li+3-Li）=3mgsinθ，可知ΔL1、ΔL2、ΔL3分别都是对应增加3个小球，所以上述是管中增加3个钢球时产生的弹簧平均压缩量.

创新型实验题一般会融合一些操作实验、生活、科技等方面的情境，通过“异中求同”的思想方法，让学生对比、联想地解决问题.这一思想方法不仅适用于实验题的解决，也可以成为学生解决未来新问题时的一种能力.

3 计算题情境分析：殊途同归

例3.（2021年广东高考物理第13题）算盘是我国古老的计算工具，中心带孔的相同算珠可在算盘的固定导杆上滑动，使用前算珠需要归零，如图5所示，水平放置的算盘中有甲、乙两颗算珠未在归零位置，甲靠边框b，甲、乙相隔s1=3.5×10-2m，乙与边框a相隔s2=2.0×10-2m，算珠与导杆间的动摩擦因数μ=0.1.现用手指将甲以0.4 m／s的初速度拨出，甲、乙碰撞后甲的速度大小为0.1 m／s，方向不变，碰撞时间极短且不计，重力加速度g取10 m／s2.

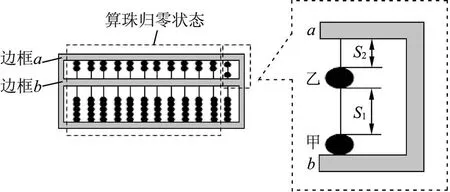
图5

（1）通过计算，判断乙算珠能否滑动到边框a；

（2）求甲算珠从拨出到停下所需的时间.

该题以算盘为情境，将中华传统文化与运动学知识相融合，渗透人文素养和科学素养.问题设计了“乙算珠能否滑动到边框a”的半开放判断问题，让学生自行寻找判断的物理量，从不同角度对问题作出有理据的判断，体现了题目解答的自主选择性和开放性.在解答过程中，学生还可采用不同的物理规律进行运算，例如动能定理、牛顿运动定律、动量守恒定律、动量定理等，最后达到同一结果.解题过程既有统一的标准，又有灵活解题方式，体现了题目设计的“殊途同归”，展现综合性的育人方式.学生在审题后需构建模型，分析情景，调用规律，进行解答.

首先，在本题题干中提到“动摩擦因数”、“甲、乙碰撞”等关键词，因此，可引导学生将真实情境进行转化，构建匀减速直线运动模型和碰撞中的动量守恒模型.

其次，针对灵活解题方式，可从以下角度促进学生分析问题和解决问题能力的提升.设甲初速度为v0，甲、乙碰撞前甲速度为v1，碰撞后甲、乙的速度分为v1′和v2′，甲乙的质量均为m.

（1）第1问的解题策略如下.

殊途1：运用动能定理和动量守恒定律.对甲碰撞前

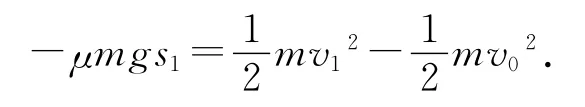
甲乙碰撞瞬间

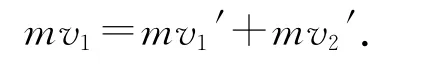
判断方法1：利用位移判断.碰后，对乙

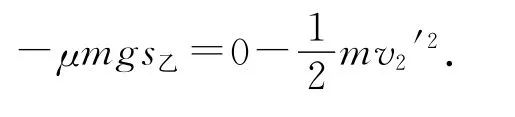
解得s乙=0.02 m=s2，所以刚好能碰到边缘a.

判断方法2：利用末速度判断.碰后，对乙

解得v乙=0，所以刚好能碰到边缘a.

殊途2：运用牛顿运动定律和动量守恒定律.

由题意可知，甲乙在导杆上运动为匀减速直线运动，甲乙的加速度都为对甲碰撞前

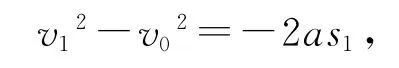
甲乙碰撞瞬间

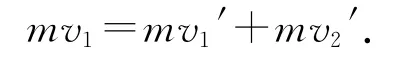
判断方法1：利用位移判断，设乙碰后到停止运动的位移为s乙，碰后，对乙

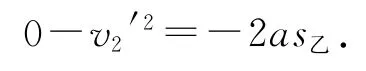
解得s乙=0.02 m=s2，所以刚好能碰到边缘a.

判断方法2：利用末速度判断，设乙最终速度为v乙，碰后，对乙

解得v乙=0，所以刚好能碰到边缘a.

同归：乙算珠能刚好能碰到边框a.

（2）第2问的解题策略如下.

殊途1：运用动量定理.

对甲碰撞前

对甲碰撞后

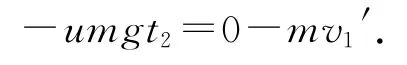
从拨出到停下所需的时间t=t1+t2=0.2 s.

殊途2：运用牛顿运动定律.

对甲碰撞前、后时间分别为

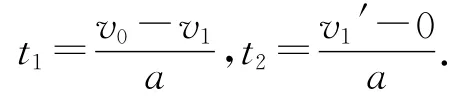
从拨出到停下所需的时间t总=t1+t2=0.2 s.

殊途3：运用v-t图，面积意义求解.

根据甲的运动情况，可画出如图6的v-t图，其所围的总面积为甲运动的位移.由几何求面积，可得

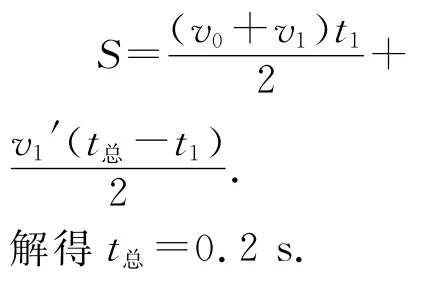
图6

同归：甲算珠从拨出到停下所需的时间为0.2 s.

通过以上多途径、深层次的思考，引导学生构建运动学的完整知识体系和深度理解运动规律，同时可以引导学生比较各种解决方法的优劣，结合自身对于规律和方法的熟练程度，择优解决方案，加强学生解决问题的能力.

在日常教学中，教师以高考题为基础，熟悉掌握一般解题思路的背景下，进行问题情境融通教学，根据不同的题型渗透诸如“正反相推”、“异中求同”、“殊途同归”等情境分析策略与思想方法，通过以情境渗透“情”，让物理教学具有温度；以实验创新“异”，让物理教学具有新度；以问题多解“途”，让物理教学具有深度，促进学生核心素养的提升.