基于热力耦合的镶嵌式机械密封端面变形分析
2021-11-04李彦启刘启东刘合荣刘明涛
李彦启 刘启东 刘合荣 刘明涛
(天津科技大学机械工程学院 天津 300222)
机械密封是矿山、石油、化工企业中机器设备的关键基础部件,一旦失效,设备将出现泄漏问题,造成机器设备运行效率降低、能源浪费、环境污染等问题。镶嵌结构式机械密封是指把密封环镶嵌到金属环座之中,使两部分之间靠过盈配合来实现扭矩传递并起到密封作用。由于装配应力的存在,使得镶嵌密封环在结构设计和参数确定上与整体密封环有较大不同,密封环镶嵌结构的微小变化都可能对镶嵌后密封环性能产生很大影响,其中以镶嵌过盈量影响最大[1]。
针对镶嵌式机械密封,国内外学者主要针对镶嵌过盈量和力变形进行分析计算,对镶嵌密封环不同温度下的变形研究较少。张明奎[2]通过使用温度下的线膨胀系数和端面摩擦力矩计算出镶嵌配合的最小过盈量,并对最大过盈量进行探讨,但未对结合面的接触应力进行相应的计算分析。高斌超等[3]建立二维轴对称热力耦合模型,分析了不同压力下的密封性能,结果表明,端面形成收敛型泄漏间隙,随着密封压力的增大,端面最小膜厚减小,温度升高。该文献虽对热力变形引起的液膜变化进行了详细的探讨,但对热力变形的规律未做详细的分析。丁雪兴等[4]对端面热变形、力变形及热力耦合变形进行了对比分析,结果表明,受力引起的变形与热变形变化趋势相反,热力耦合变形位于两者之间。但该文献未对结构参数与温度场之间的关系进行研究。张书贵和顾永泉[5]通过有限元法计算了密封环的温度场,分析了影响密封环温度场的各种因素,分别探讨了热变形与力变形的变形规律,但该文献并没有考虑热力耦合作用下的变形规律。周剑锋和顾伯勤[6]建立了机械密封环的传热模型,认为端面液膜承载力和泄漏率均随转速的增加而增加。该文献虽详细分析了端面变形对液膜的影响,但未深入探讨温度对端面变形的影响。
本文作者以实际工程应用的某双端面机械密封为研究对象,建立密封环的传热模型,利用有限元数值法计算得到温度场。综合密封环的受力边界条件,建立热力耦合模型,研究密封环的过盈量和厚度对密封环端面变形的影响规律,为该机械密封结构的进一步优化提供理论依据。
1 机械密封模型
1.1 几何模型
文中研究采用的是某公司研发的双端面式密封,其主要结构参数为:动环内径D1=61.34 mm,动环外径D2=74.64 mm,动环座外径D3=79.64 mm。机械密封动环及动环座结构如图1(a)所示。
由于机械密封动环组件在几何形状、边界条件以及其他外界条件都对称于旋转轴(过旋转轴的任一平面都是对称面),其在ANSYS有限元计算中可以简化为轴对称模型。动环组件轴对称模型如图1 (b)所示。

图1 动环组件结构及轴对称模型Fig 1 Moving ring assembly structure and axisymmetric model (a)moving ring assembly structure; (b)ANSYS axisymmetric model
1.2 传热模型
动环及动环座的材料属性如表1所示。

表1 动环组件材料参数Table 1 Material parameters of moving ring assembly
动环组件的工作参数为:密封介质压力3 MPa,主轴转速2 000 r/min,密封腔温度22 ℃。
为方便计算,简化模型,对该机械密封作以下假设[7]:
(1)密封环温度场以及受力边界条件加载均为轴对称;
(2)由于密封环温度主要是由摩擦产生,忽略搅拌所产生的热量;
(3)该机械密封泄漏量较少,忽略泄漏及热辐射所带走的热量;
(4)密封环及密封介质的材料属性不随温度的变化而变化。
文中是在机械密封工作状态下进行端面变形分析,传热系统中各点的温度仅随位置的变化而变化,不随时间的变化而变化,属于稳态热分析。稳态热平衡微分方程[8]为
(1)
在二维轴对称稳态温度场中,导热微分方程[8]为
(2)
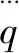
1.3 摩擦热计算
该机械密封密封端面处于混合摩擦状态,在动环端面因摩擦产生的热量按下式计算[1]:
Q=fpcvAf
(3)
式中:f为摩擦因数;pc为端面比压;v为密封平面的平均线速度;Af为密封面面积。
动环热流密度采用以下公式计算[1]:
q=fpcv
(4)
1.4 热分配系数计算
由于文中只对动环组件进行计算,密封端面摩擦产生的热量会传递给动环和静环,因此需要将理论计算所得的摩擦热量按一定比例分配给动环。考虑到动、静环材质、尺寸等条件不同,动、静两环所获得的端面摩擦热量也不相同,必须对热量进行合理的分配。根据二维稳态计算公式:
(5)
式中:h为环的轴向厚度;y为动、静环端面距离。
由于端面温度连续性条件存在,动、静环接触端面间温度相等,即可用下式表达[9]:
(6)
式中:s代表静环;r代表动环。
1.5 对流换热系数
对流换热系数的计算采用Tachibana公式[10]:
(7)
式中:Nu为努塞尔常数;Pr为普兰特常数;k2为密封介质导热系数;Cp为密封介质比热容;μ为流体动力黏度;νf为流体运动黏度;D2为密封环对应边界处直径;U为密封环对应边界处线速度;k1为流体导热系数。
1.6 热力耦合模型
密封环发生变形的主要原因是受力载荷和密封间隙产生的摩擦热的影响。在对密封环变形的数值分析中,当出现2种或者2种以上物理场共同作用时,就需要对模型进行耦合分析。热力耦合分析就是对密封环受力变形和受热变形进行统一计算。热力耦合根据耦合计算机制不同可以分为直接耦合法和分离耦合法。直接耦合法是在同一求解器中同时求解固体和温度控制方程,而分离耦合法是指在耦合面处,将计算得到的温度场加载到固体结构中,该方法又称为单向耦合[11]。文中采用单向热力耦合方法进行计算,具体计算步骤为先对密封环组件施加传热边界条件,如热流密度、对流换热系数等,计算出该结构的温度分布和热应力,然后将计算得到的结果作为边界条件传递给密封环结构进行静应力分析,从而得到密封环变形量等数据。其在ANSYS中单向热力耦合模型如图2所示。
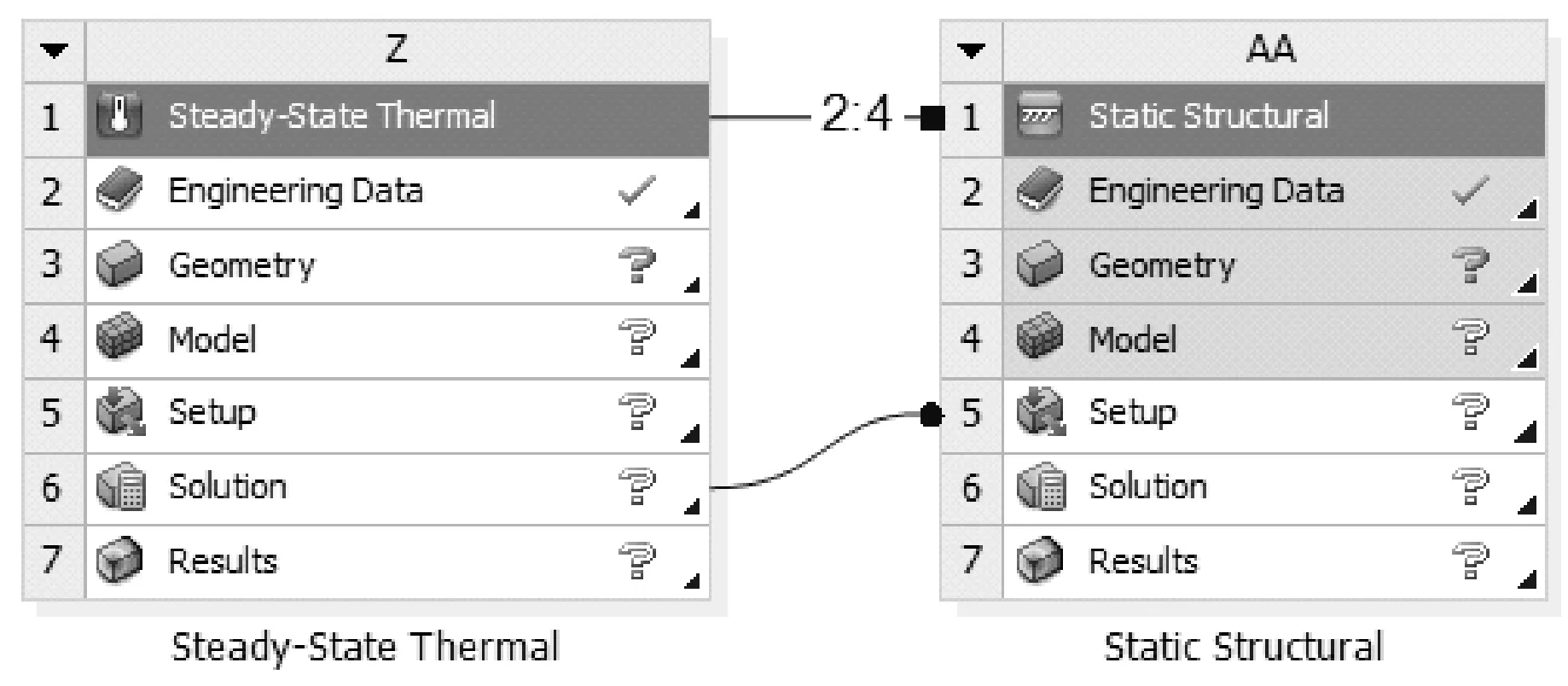
图2 单向热力耦合模型Fig 2 One-way thermo-mechanical coupling model
1.7 边界条件
动环组件边界条件如图3所示。动环座外表面CD与DE与密封介质接触,受到密封介质压力的作用,该面与密封介质发生对流换热,根据公式(7)其对流换热系数为α=7 117.39 W/(m2·℃);动环表面CB与密封介质接触,受密封介质压力作用并与密封介质发生对流换热,因该面积十分小,忽略不计;密封端面AB受端面间隙液膜反力,该液膜反力沿径向呈线性分布,同时端面为摩擦热来源,根据公式(4)施加热流密度q=1.34×105W/(m·℃);动环内径AJ和JI与空气接触,其所受大气压力和对空气的对流换热忽略不计;EF面为固定面,其远离端面,做绝热处理;FG与GH面由于受到的密封圈压力很小,忽略不计。

图3 动环组件边界条件Fig 3 Boundary conditions of moving ring assembly
2 过盈量对端面变形的影响
2.1 过盈量计算
对于镶嵌式机械密封,动环和动环座的镶嵌不当是造成密封失效的主要原因之一。过盈量过大,会使得动环所受径向压力增大,发生塑性变形和密封环的碎裂;过盈量太小,会造成密封环与环座发生相对转动或者脱落,使得机械密封无法工作。同时,由于在装配过程会产生装配应力,使得镶嵌密封环在结构设计、参数确定、应用条件等方面与整体密封环有较大的不同,密封环镶嵌结构的微小变化都可能对机械密封的整体性能产生较大的影响。因此,对机械密封的过盈量进行研究十分必要[12]。
过盈量的计算由两部分组成:一是在工况温度下由于动环与动环座线膨胀系数不同造成过盈量变化;二是平衡摩擦副端面摩擦力矩的过盈量。
(1)由不同线膨胀系数产生的半径过盈量δ1
因动环与动环座线膨胀系数不同而产生的半径过盈量δ1按下式计算:
δ1=TR2(α1-α2)
(8)
式中:α1为动环座的线膨胀系数;α2为动环的线膨胀系数;T为密封腔工作温度与室温的差值;R2为动环与动环座结合处半径。
(2)平衡摩擦副端面摩擦力矩的半径过盈量δ2
根据过盈配合界面的摩擦阻力矩大于密封面的摩擦力矩,由过盈产生的结合压力p有下列关系:
(9)
式中:f1为端面动摩擦因数;f2为静摩擦因数;pc为端面比压,Pa;R1为动环内径半径,mm。
动环座在结合压力p作用下产生的位移u1为
(10)
式中:E1为动环座的弹性模量,Pa;μ1为动环座的泊松比;R3为动环座外径半径。
动环在结合压力p作用下产生的位移为
(11)
式中:E2为动环的弹性模量,Pa;μ2为动环的泊松比;pc为端面比压。
平衡摩擦副端面摩擦力矩的半径过盈量δ2为
δ2=u1-u2
(12)
(3)最小半径过盈量δmin
δmin=δ1+δ2
(13)
经计算,最小过盈量为13.7 μm。
最大过盈量受动环组件材料强度限制。动环座受拉力,其内径最大应力不应该超过屈服强度极限σs。其表达式如下式所示:
(14)
动环受压力,其外径的最大应力不应该超过材料的抗压强度σs。其表达式如下式所示:
(15)
取两者中最小压力p为结合压力,其余算法与最小过盈量算法一致。经计算求得:
δmax=161.34 μm
2.2 过盈量设置
在ANSYS仿真计算中,过盈配合属于典型的非线性接触问题。用几何尺寸控制过盈量并不能确定初始接触状态,其接触状态的确定是依据网格划分。在网格划分的过程中,几何尺寸所规定的过盈量会因为误差导致失效,大大降低计算精度甚至无法达到计算要求[13]。过盈量的设置可以通过以下2种方法实现[14]:一种是在建立接触对条件下使用OFFSET命令的偏移量来表达过盈量;一种是通过设置接触单元的关键字选项KEYOPT(9)=4,把目标面和接触面上的单元设置为刚好接触的位置,没有间隙和过盈,同时该命令使得程序在判定初始接触状态时只考虑用实常数CNOF的值来表达过盈量。OFFSET和CNOF正值为过盈量,负值为间隙量。文中采用第一种方法来设置过盈量。
2.3 计算模型验证
文献[15]实验测量了密封环镶嵌后的端面变形量,为验证文中所建立的热力耦合仿真计算模型,采用文中的仿真计算模型对文献[15]所给出研究对象进行计算,文献[15]中的材料参数如表2所示,其动环内径为76.9 mm,外径为83.8 mm,动环座外径为88.3 mm。

表2 文献[15]动环组件材料参数Table 2 Material parameters of moving ring assembly in reference[15]
经过仿真计算,动环座最上端点尺寸为88.798 mm,实验测得最上端点尺寸为88.732 mm,计算结果与实验结果相差不大,仿真计算模型可以满足计算要求。
2.4 计算结果及分析
图4为动环综合应力云图,其最大综合应力发生在靠近内径的密封端面处。这是由于动环端面温度梯度中内径处温度最高,热应力较大,动环组件温度场的分布如图5所示。

图4 动环综合应力云图Fig 4 Comprehensive stress nephogram of moving ring

图5 动环组件温度分布云图Fig 5 Temperature distribution nephogram of moving ring assembly
为方便观察,设动环内径处为路径起始处,外径设为路径终止处,在接触端面的路径上选取节点以观察端面变形量。将靠近动环端面的轴向方向设为正方向,图6示出了端面分别在力、热、热力耦合下的端面变形情况。可知,只分析力载荷端面向动环方向变形,动静环之间呈发散间隙;只分析热载荷端面向静环方向变形,动静环之间呈收敛间隙;热力耦合变形曲线靠近热变形曲线,说明端面变形受热应力的影响较大。

图6 力、热和热力耦合端面变形曲线Fig 6 Deformation curves of mechanical,thermal and thermal coupling end face
为方便观察,设动环左端面为路径起始处,右端面(即动环和静环接触端面)为路径终止处。图7所示为在不同过盈量下动环和动环座接触面的应力值,可见,随着过盈量的增大,动环和动环座之间结合面接触应力不断增大。

图7 不同过盈量下结合面接触应力Fig 7 Contact stress of joint surface under different interference
图8所示为不同过盈量下端面变形规律。可知,随着过盈量的增大,密封端面变形也不断增大。在研究的4种过盈量情况下,其内径处的变形量大于外径处,密封端面形成收敛间隙。
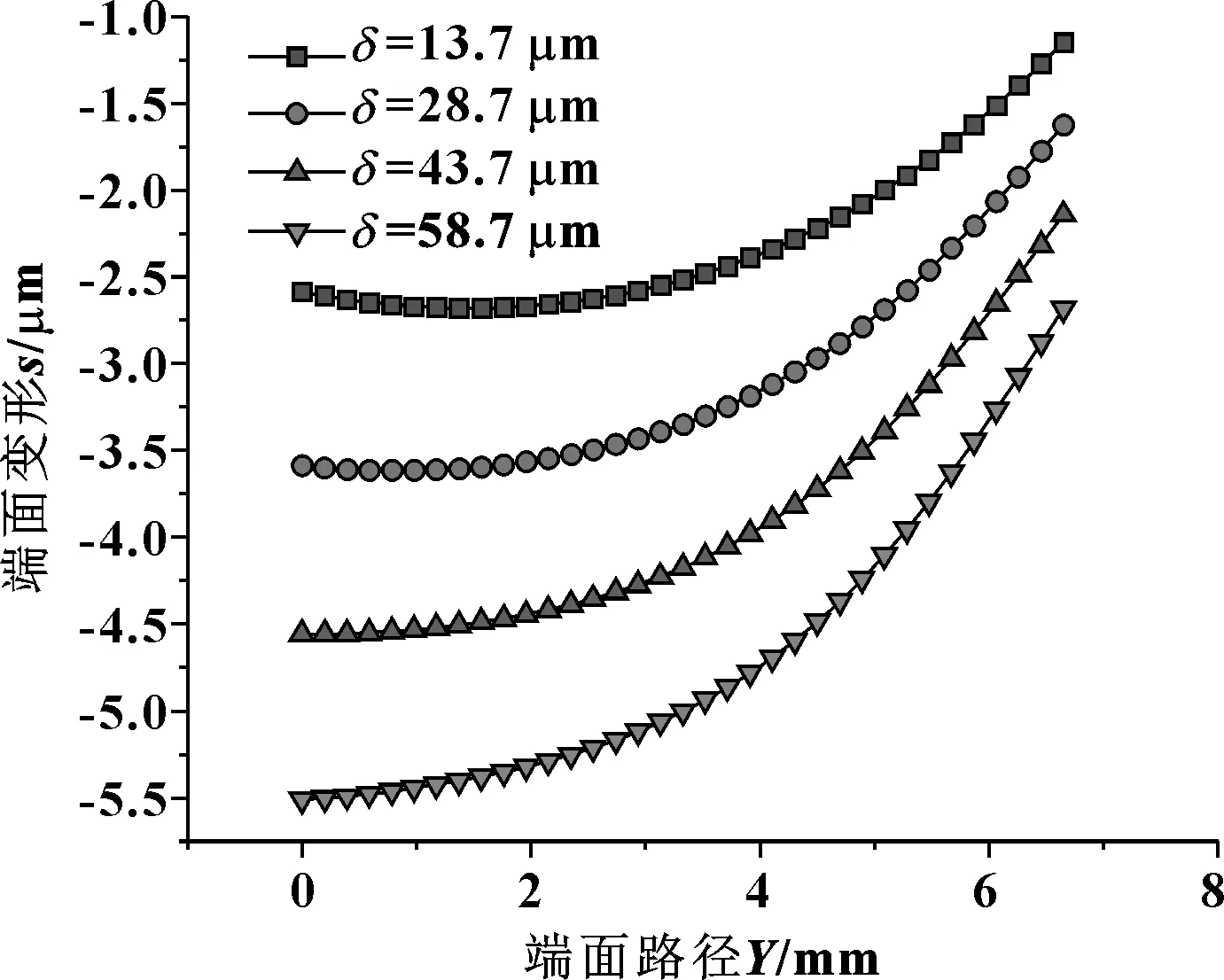
图8 不同过盈量下端面变形量Fig 8 Deformation of end face under different interference
3 动环厚度对端面变形的影响
动环是机械密封装置核心零部件,其厚度对热分配系数有至关重要的影响,进而影响整个动环组件的温度场。
设动环内径为起始处,动环外径为终点处,从而建立动环端面观察路径。由图9可知,动环组件的最高温度在动环内径处,这是因为由密封端面产生的热量主要通过与密封介质的对流换热被带走,而动环内径处是与空气接触,其与空气的对流换热系数较小,散热较慢,造成内径处温度较高。同时,随着动环厚度增加,其最大温度也是不断下降的。这是因为随着动环厚度的不断升高,其热分配系数在不断降低,从而动环所得到的热流密度也不断降低,整个动环组件温度场发生改变。
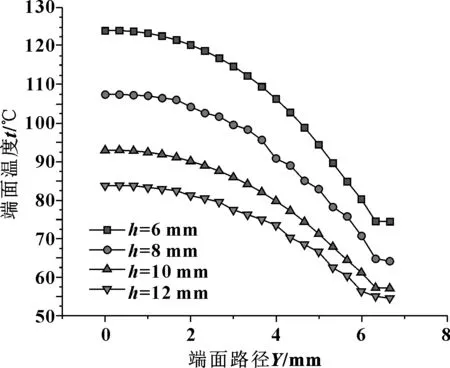
图9 不同动环厚度端面温度分布Fig 9 Temperature distribution on the end face of different moving ring thickness
图10示出了不同动环厚度下端面应力分布情况。可知,随着动环厚度增大,端面内径处应力不断下降。这是由于端面温度减少所导致,对比图9和图10,其变化曲线是一致的,端面温度对动环端面综合应力有较大的影响。

图10 不同端面厚度下端面应力分布Fig 10 Stress distribution of end face under different end face thickness
图11示出了不同动环厚度下的端面变形量的变化情况。可知,随着动环厚度的不断增大,内径处的变形量不断降低,而外径处的变形量不断增加,端面间隙由收敛型变成发散型。一方面是因为动环厚度的增加导致温度场发生改变,内径处温度和所受应力降低导致内径变形量逐渐减小;另一方面则是由于动环座与动环的结合面的接触比降低,随着动环厚度的增大,动环最大综合应力从内径处转移到动环组件结合面处,导致密封环外径所受应力增大,如图12所示。发散型间隙会导致内径处液膜压力降低,同时该结构类型也大大增加了内径处的泄漏量。
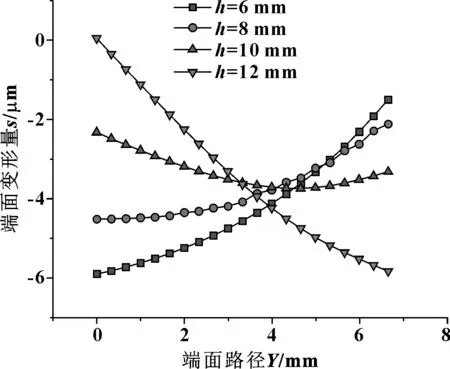
图11 不同动环厚度端面变形量Fig 11 Deformation of end face of different moving ring thickness

图12 不同动环厚度时最大应力位置Fig 12 Maximum stress position of different moving ring thickness (a)moving ring thickness is 6 mm; (b)moving ring thickness is 12 mm
4 结论
(1)通过建立热力耦合模型,对比分析热、力和热力耦合对端面变形的影响规律,结果表明,热应力对端面变形的影响大于结构应力,故不能忽略热应力对机械密封动环组件的影响。
(2)过盈量对端面变形有着至关重要的影响,过盈量越大,动环与动环座结合面的接触应力就越大,端面变形也越大。动环最大应力发生在接触端面内径处,端面朝着静环方向发生轴向变形。
(3)动环厚度对机械密封温度场有着较大的影响。随着动环厚度的增大,其温度和内径处的应力呈下降趋势。在动环厚度增大的过程中,内径处变形由大变小,外径处变形由小变大,端面间隙发生了从发散型到收敛型的转变,大大增加了泄漏量。
