基于叶轮转子系统下的干气密封轴向振动分析*

张伟政 姜 娥 林 智 丁雪兴

(兰州理工大学石油化工学院 甘肃兰州 730050)

干气密封是一种采用气体作为密封介质的新型机械密封，和传统的机械密封相比，具有无磨损、功耗小、零泄漏等优点。近年来，干气密封动力学的探究有了一定的理论成果。丁雪兴等[1]通过求解非线性雷诺方程，得出气膜涡动刚度的近似解析解，并获得在不同介质、压力及转速下螺旋角的最佳取值。张伟政等[2-4]通过求解气膜推力，并以此力为激振力，利用龙格-库塔法求解气膜-密封环轴向受迫振动方程，探讨分析螺旋角及槽深对静环振动的影响规律；考虑干气密封角向摆动干扰，求解振动方程，获得稳定的结构参数取值范围。俞树荣等[5]分析了螺旋角对干气密封系统稳定性的影响，并给出了使系统稳定的螺旋角的范围。彭旭东等[6]基于完全析因设计方法，考虑干气密封的动压效应以及轴向气膜稳定性，对中低压螺旋槽几何结构参数进行了优化。俞树荣等[7]通过运用Maple软件，对气膜轴向和角向阻尼系数的近似表达式进行求解，考虑不同介质压力及转速，研究获得到稳定性最佳螺旋角取值。丁雪兴等[8]考虑了热耗散变形会对干气密封产生影响，对气膜-密封环系统进行非线性轴向动力学建模，通过Floquet指数的求解，研究得到系统振动稳定性最佳的螺旋角取值。但随着经济发展，离心式压缩机、离心泵等旋转机械向高性能、高效率、大容量等高参数方面发展，使得转子、轴承、密封之间的耦合作用越来越显著，大系统的动力学问题越来越突出。设备处于高速运转工作状态时，叶轮由于内部流场流固耦合作用，会在各个叶片流道产生不同的力，如流体激振力或压力[9]，而各个力综合起来会在轴向产生一个轴向分力。而干气密封动静环间隙为3～6 μm，轴系的轴向振动极为可能导致间隙发生变化，造成动静环发生摩擦碰撞，导致干气密封失效。因此，只考虑干气密封系统动力学的研究已经不能满足现代实际工业的需求，基于叶轮转子系统下的干气密封轴向振动分析尤为重要。

本文作者基于干气密封结构特性，对叶轮转子-轴承-干气密封大系统进行轴向振动数学建模，利用待定系数法，推导求出动、静环轴向振动幅值表达式，分析其影响因素。利用SolidWorks三维建模建立叶轮转子-轴承-干气密封系统几何模型，运用ANSYS Workbench有限元分析软件进行模拟仿真计算，得出动静环位移响应-频率曲线。最后结合理论结构和模拟对比分析，得出其影响规律特性。

1 叶轮转子-轴承-干气密封轴向振动动力学模型建立及求解

建立如图1所示的叶轮转子-轴承-干气密封系统模型。

图1 叶轮转子-轴承-干气密封系统模型Fig 1 Model of impeller rotor-bearing-dry gas seal system

模型假设：

(1)将叶轮转子-轴承-干气密封系统看作是双自由度受迫振动；

(2)干气密封动静环间的气膜假设为具有刚度的弹簧；

(3)叶轮激振力假设为简谐激振力，静环的轴向位移假设为简谐运动。

根据干气密封动静环结构特性[10]及叶轮转子-轴承-干气密封系统几何模型(如图1所示)，建立轴向振动模型如图2所示。

图2 叶轮转子-轴承-干气密封系统轴向振动模型Fig 2 Axial vibration model of impeller rotor- bearing-dry gas seal system

图2中：m1为动环、轴承、转轴及叶轮转子的总质量；m2为静环的质量；K1为轴承刚度；K2为气膜刚度；K3为加载弹簧刚度；C1为轴承阻尼；C2为气膜阻尼；x1为动环振动位移；x2为静环振动位移。假设作用在2个质量块m1和m2上的力分别为简谐激力F1(t)和F2(t)，其大小为Fi(t)=Fisinωt。

取广义坐标(x1,x2)，以静平衡位置为坐标原点，根据牛顿定律分别写出2个运动方程：

(1)

整理得：

(2)

由于气膜阻尼和轴承刚度阻尼相对气膜刚度很小，故忽略不计，式(2)化简得：

(3)

设特解为x1(t)=X1sinωt，x2(t)=X2sinωt,X1和X2为振幅待定值，代入式(3)得：

(4)

求解式(4)，得系统轴向振动幅值表达式为

(5)

由于m1通常为20～50 kg，而m2通常为0.2～0.5 kg，因此m1>>m2，故m2近似取值为0。文中只考虑叶轮转子激振力对干气密封的影响，忽略静环的受力，即F2=0；气膜刚度K2通常为100～2 000 N/μm，轴承刚度K1通常为1 000～10 000 N/μm，加载弹簧刚度K3通常为0.02～0.03 N/μm[11]，因此K1>>K3，K2>>K3，故K3近似取值为0。

将m2=0，F2=0，K3=0代入式(4)和式(5)化简得：

(6)

分析式(6)可发现，由于K1和m1为确定值，此时的动、静环的位移幅值X1、X2只与转速ω及简谐激力F1(t)有关，表达式中不包含气膜刚度K2，即说明此时动、静环的位移幅值X1、X2气膜刚度K2无关。文中叶轮转子-轴承-干气密封的轴系的设计工作转速在10 000 r/min，远低于一阶临界转速，符合设计要求。比较动、静环的位移幅值X1、X2发现，动、静环的位移幅值X1、X2相等，说明此时的动静环间的追随性高，当轴系受到外界激振力干扰时，动环发生轴向振动位移，静环追随着发生相应幅值的振动位移，其间隙是趋于稳定的，即动静环不会发生摩擦碰撞，保证了系统的稳定运行。

2.螺旋槽干气密封基于叶轮转子系统的轴向振动分析

2.1 叶轮转子-轴承-干气密封几何模型的建立

(1)干气密封结构由静环、动环及轴套等零件组成。在设备正常运转时，由于流场动压效应，动环与静环之间形成一层极薄(微米级)且具有一定刚度的气膜，而在谐响应振动分析中，无法用流场模拟气膜状态，于是将这层极薄的气膜简化为弹簧刚度约束。

(2)当设备正常运转时，叶轮处于一个温度场、流场、力场等多物理场耦合作用下的复杂工作环境，叶片会受到非定常压力场及不平衡的激励，导致叶轮引起不平衡响应。文中主要以叶轮的不平衡量为激励载荷，忽略叶片及其他复杂结构，将叶轮系统简化成圆盘转子模型。

(3)假设不考虑轴承的阻尼影响，只考虑轴承对轴系支承正刚度的作用，将轴承简化为弹簧支撑约束。

轴的尺寸[12]如图3所示，在轴z4、z6部分加载轴承约束，在z8部分放置干气密封系统，在z9部分放置叶轮转子系统。

图3 轴尺寸示意Fig 3 Schematic of shaft size

螺旋槽干气密封动环螺旋槽槽数为12，内外半径分别为68、92 mm，槽根半径为82 mm，静环内外半径分别为72、92 mm[13]。叶轮出口半径为208 mm，进口半径为105 mm，叶片出口宽度为22 mm，叶片进口宽度为55 mm。利用SolidWorks三维软件建立叶轮转子-轴承-干气密封系统几何模型，如图4所示，其主要材料参数见表1。将模型导入Workbench软件中，转轴选用Hex Dominant网格划分法，单元大小为6 mm；叶轮选用Face Meshing及Hex Dominant网格划分法，单元大小为6 mm；轴套选用Face Meshing及Hex Dominant网格划分法，单元大小为4 mm。由于动环螺旋槽槽深是微米级，而整个轴系是毫米级，跨度较大，且在轴向振动中将流体动压效应引起的流场效果简化为弹簧约束，故忽略螺旋槽槽深的影响，文中分析将螺旋槽槽深轴向放大1 000倍。动静环都选用Automatic网格划分法，单元大小为1.5 mm。模型中的单元总数为108 832，节点总数为281 009。

图4 叶轮转子-轴承-干气密封几何元模型Fig 4 Finite element model of impeller rotor- bearing-dry gas seal system

表1 材料性能参数Table 1 Material performance parameters

2.2 边界条件

2.2.1 轴承约束

在转轴的轴承安装位置处沿圆周方向均布4个弹簧单元来模拟轴承的弹性支承[14]，布置方式如图5所示。其中弹簧单元外端施加固定约束，内端接触主轴处施加轴承刚度。

图5 弹簧单元布置Fig 5 Spring unit layout

文中采用角接触球轴承，根据经验公式[15]可知，角接触球轴承的径向刚度为

K=0.118×104(DwFZ2cos5α)1/3

(7)

代入轴承参数，滚动体个数Z为19，滚动体直径Dw为22.25 mm，初始接触角α为32.5°，径向力F为1 000 N,可得K=176.957 N/μm。

2.2.2 弹簧约束

在动静环间均布4个弹簧单元,静环与静环座间的加载弹簧则简化为在静环背面均布4个弹簧单元，弹簧另一端施加固定约束。由于静环座是固定的，静环只能沿轴向运动，因此在静环施加Remote Displacement约束，限制静环的所有方向旋转自由度以及Y和Z方向的平移自由度，释放X方向的平移自由度(即轴向平移自由度)。

2.3 模拟计算结果与分析

建立干气密封在叶轮转子系统下的轴向受迫振动和谐响应的对应关系[16]，根据谐响应的激励载荷、位移幅值及频率随时间变化和运行条件的变化规律，模拟干气密封在叶轮激励作用下的轴向受迫振动，并作出定性、定量分析。文中采用谐响应完全法对干气密封基于叶轮转子下轴向振动进行模拟仿真分析。

2.3.1 气膜刚度对轴向振动的影响

为探究气膜刚度对轴向振动的影响规律，弹簧刚度取值0.03 N/μm，将不同的气膜刚度值(1 000、1 200、1 400、1 600、1 800、2 000 N/μm)分别输入动静环间的模拟弹簧单元；在叶轮转子轴截面施加一个轴向简谐力，幅值为10 N；设定频率求解范围为0～1 500 Hz，运算次数为1 500次，即每次求解间隔为1 Hz。

取动环、静环为响应体，方向为x轴方向即轴向，得到不同螺旋槽槽深的动环及静环的轴向位移响应-频率曲线，截取峰值频率段120～200 Hz，如图6、图7所示，其最大位移幅值如表2所示。

图6 不同气膜刚度静环位移响应-频率曲线Fig 6 Displacement response-frequency curves of static ring under different gas film stiffness

图7 不同气膜刚度动环位移响应-频率曲线Fig 7 Displacement response-frequency curves of moving ring under different gas film stiffness

表2 不同气膜刚度下动环及静环最大位移幅值Table 2 Maximum displacement amplitude of moving ring and static ring under different gas film stiffness

分析位移响应-频率曲线图6、7可发现：当弹簧刚度取值0.03 N/μm，在激振力幅值恒定不变的条件下，不同气膜刚度下动静环引起的位移响应的频率一致，均在130 Hz附近处出现波峰，说明当激励频率达到130 Hz时系统发生共振，使得动静环位移响应剧增。观察位移响应曲线，发现当越过波峰频率后，位移响应随着激振频率的提升而下降，并趋于平稳，这说明激振力引起的干扰振动随频率的提升而衰减，即系统在高速工作状态下是趋于稳定状态，也验证了在实际工程中干气密封能在高速条件下稳定运行。

分析表2可发现，当激振力幅值恒定不变时，随气膜刚度的增加，动、静环的位移响应幅值呈现递减趋势，这符合气膜刚度越大越稳定的规律。比较位移响应数值发现，改变气膜刚度，动、静环位移响应幅值变化不大，这是由于弹簧刚度取值为0.03 N/μm，远小于气膜刚度值100～2 000 N/μm，在这个跨度下改变气膜刚度数值，对动静环的振动影响不大，这与式(6)不含气膜刚度K2的原因相符。

结合图6、7、表2分析，动、静环发生位移响应的频率一致，且动静环位移幅值也相同，这与式(6)呈现的规律相符，振动频率相同，位移幅值相同，说明了干气密封动静环的追随性高。当受外界激振力干扰时，静环追随动环发生相等位移振动，间隙稳定，从而保证干气密封系统能稳定运行。

2.3.2 激振力对轴向振动的影响

为探究激振力对干气密封轴向振动的影响规律，弹簧刚度取值0.03 N/μm，气膜刚度恒定取值1 400 N/μm，其他载荷及参数设置不变，改变叶轮轴向力的幅值，分别取10、20、30、40、50 N。取动环、静环为响应体，方向为x轴方向即轴向，得到不同激力下轴向位移响应-频率曲线，截取峰值频率段120～180 Hz，如图8、图9所示，其最大位移幅值如表3所示。

图8 不同激振力下静环的位移响应-频率曲线Fig 8 Displacement response-frequency curves of static ring under different excitation forces

图9 不同激振力下动环的位移响应-频率曲线Fig 9 Displacement response-frequency curves of moving ring under different excitation forces

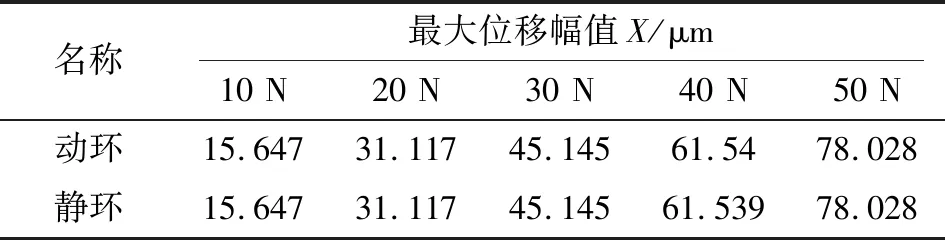
表3 不同激振力下动环及静环最大位移幅值Table 3 Maximum displacement amplitude of dynamic ring and static ring under different excitation forces

结合位移响应-频率曲线图8、图9及表3中最大位移幅值分析可发现：激振力的大小和动、静环的位移幅值成正比关系。随着激振力的增大，动、静环的位移幅值也随着增大，且激振力的大小与动、静环的位移幅值呈正比，这与式(6)相符合。这说明激振力严重影响干气密封的稳定性，要提高干气密封的稳定性，叶轮的轴向激振力就必须要平衡好。

表3中动、静环在同一激振力下的位移幅值相等，这与表2呈现的规律及原因一致。

3 结论

(1)基于干气密封结构特性，在忽略阻尼的条件下，对叶轮转子-轴承-干气密封系统建立双自由度轴向振动动力学模型，并利用待定系数法，求解获得了在简谐激力下动静环振动幅值的表达式。比较动、静环的位移幅值X1、X2,发现动、静环的位移幅值X1、X2相等，说明此时的动静环间的追随性高，当轴系受到外界激振力干扰时，动环发生轴向振动位移，静环追随着发生相应幅值的振动位移，其间隙是趋于稳定的，即动静环不会发生摩擦碰撞，保证了系统的稳定运行。

(2)利用三维建模软件SolidWorks对含静环的叶轮转子-轴承-干气密封系统进行几何建模，并运用ANSYS Workbench有限元分析软件进行模拟仿真计算，研究气膜刚度和激振力对轴向振动的影响。结果表明：在其他条件不变的情况下，改变槽深，即改变气膜刚度数值，对动、静环振幅影响不大，动、静环的振动频率相同、位移幅值相同，说明动、静环的追随性高，其间隙稳定，从而保证干气密封系统的稳定性；在其他条件不变的情况下，当激振力变化时，动、静环位移幅值与激振力成正比关系，说明激振力严重影响干气密封的稳定性，要提高干气密封的稳定性，叶轮的轴向激振力就必须要平衡好。