斜腹板薄壁箱梁横向内力的改进分析方法

王晨光，张元海，汪洋生

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

箱形梁在高强、薄壁、轻型化、不设跨内横隔板等发展趋势下，其横向受力性能突出，较大的横向内力往往在箱形梁顶底板与腹板相交处产生纵向裂缝，威胁到桥梁的安全运营。近年来，国内外许多学者已在箱形梁的横向内力方面开展了大量研究。分析箱形梁横向内力的方法总体上可分为影响面图表法、平面框架法、有限元法等。郭金琼等[1]在对理想边界的板进行弹性分析后绘制影响面图表来进一步计算横向弯矩。平面框架法采用合理的假设将复杂的空间体系转换为二维平面结构，运用解析法得到计算横向内力的一般公式。项贻强等[2]将横梁比拟为弹性支承连续梁，提出了采用弹性支承连续梁法对梁系桥跨结构进行横向受力分析的实用方法。应用框架分析法对波形钢腹板箱形梁横向内力进行分析，成为了近年来的研究热点之一[3-8]。赵品等[3]对波形钢腹板箱梁腹板与顶板的线刚度比进行了研究，探讨分析了线刚度比对波形钢腹板箱梁横向内力的影响。乔朋等[6]在对单箱多室波形钢腹板组合箱梁腹板剪应力进行研究基础上，分析了荷载类型及作用位置对腹板剪应力的影响。黎雅乐等[7]对波形钢腹板箱梁与混凝土箱梁顶板上的横向内力进行了对比分析，提出了设计参考值。汪洋生等[9]对薄壁箱梁横向内力进行分析之后，提出了箱形梁横向弯矩的修正系数，以便设计人员应用。Lin等[10]对组合结构中混凝土桥面板与钢梁螺栓连接件在横向弯矩作用下的受力性能进行了研究。采用有限元法分析箱形梁的横向内力也是目前广泛采用的方法之一[11-15]。钟新谷等[11]采用一种简单有效的有限元法建立了计算箱形梁横向内力的单元刚度矩阵，并对箱形梁角点弯矩进行了分析。文献[12-13]研究分析了车辆荷载对单箱室箱形梁的影响，基于有限元法提出了横向内力的修正理论。郑震等[16]在矩形截面箱形梁横向内力计算理论的基础上，提出了计算带悬臂板斜腹板箱梁横向内力的计算理论，即推广的TYL法。这种方法为分析箱形梁横向内力提供新的思路，但在分析过程中采用的薄片框架计算模型与实际情况不符。

本文在推广的TYL框架分析法的基础上，建立了满足平衡条件的新的计算模型，并分析得到计算箱形梁横向内力的解析公式。在此基础上，与Ansys有限元法相结合，通过工程实例详细分析了两种不同计算方法对箱形梁横向弯矩的影响。

1 改进分析方程的基本原理

求解箱形梁横向弯矩时，沿箱梁跨度方向虚设横向及纵向连续支承，再截取单位长度的薄片框架，其横截面尺寸及虚设支承见图1。图1中：A、B、C、D分别为箱室的4个角点；a、b、c分别为箱室腹板、顶板、底板的长度；b1为翼缘板的长度；bs为顶板全长；ts、tf、tx分别为顶板、腹板、底板的厚度；h为梁高。偏心荷载q(z)作用在顶板上，偏心距为e。在计算得到支承反力和无侧移薄片框架弯矩后，释放虚设支承，并在相应位置处施加大小相等方向相反的力。箱形梁的最终横向弯矩即反力作用下的横向弯矩与无侧移框架的横向弯矩这两部分的叠加。

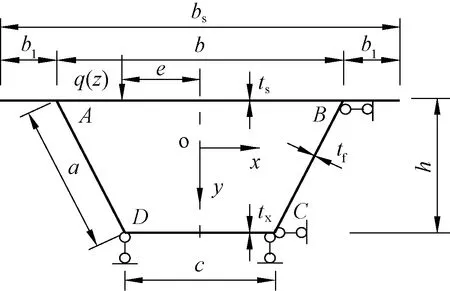
图1 横截面尺寸与虚设支承

1.1 框架位移与畸变位移的协调关系

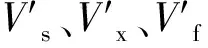
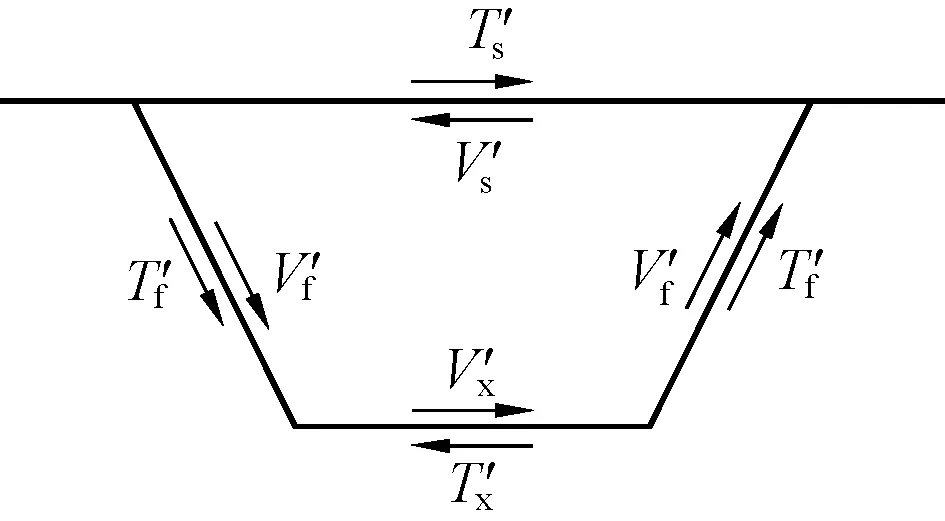
图2 框架的剪力差荷载

薄片框架为对称结构，在反对称荷载作用下结构产生的横向变形具有反对称性。因此，箱形梁顶板和底板上的反弯点应当在对称轴上，即顶板与底板的中点处。Qs、Qx分别为顶、底上反弯点处的内剪力。假设腹板上的反弯点使其上下两部分的长度之比为1/ηm。ηm为与箱梁横截面尺寸有关的系数，Qf为腹板上反弯点处的内剪力，见图3。

图3 框架内剪力示意

由薄片框架角点处弯矩平衡条件，可得各板件内剪力之间关系为

(1)

(2)

推广的“TYL”框架分析法基于畸变理论的框架模型来计算薄片框架位移，这种模型直接在底板两角点处加支座，见图4(a)。但采用这种模型计算求解得到的底板内剪力Qx、顶板内剪力Qs与畸变水平分力F不能满足平衡条件，即Fh≠(Qs+Qx)c。

为更准确地计算箱形梁的横向内力，反映箱形梁横向内力的变化规律，建立合理的计算模型是十分必要的。根据结构变形的反对称性以及在反弯点上弯矩为零的性质，取一半结构建立计算模型，见图4(b)。该计算模型物理概念明晰，能够更好地反映力的平衡关系。

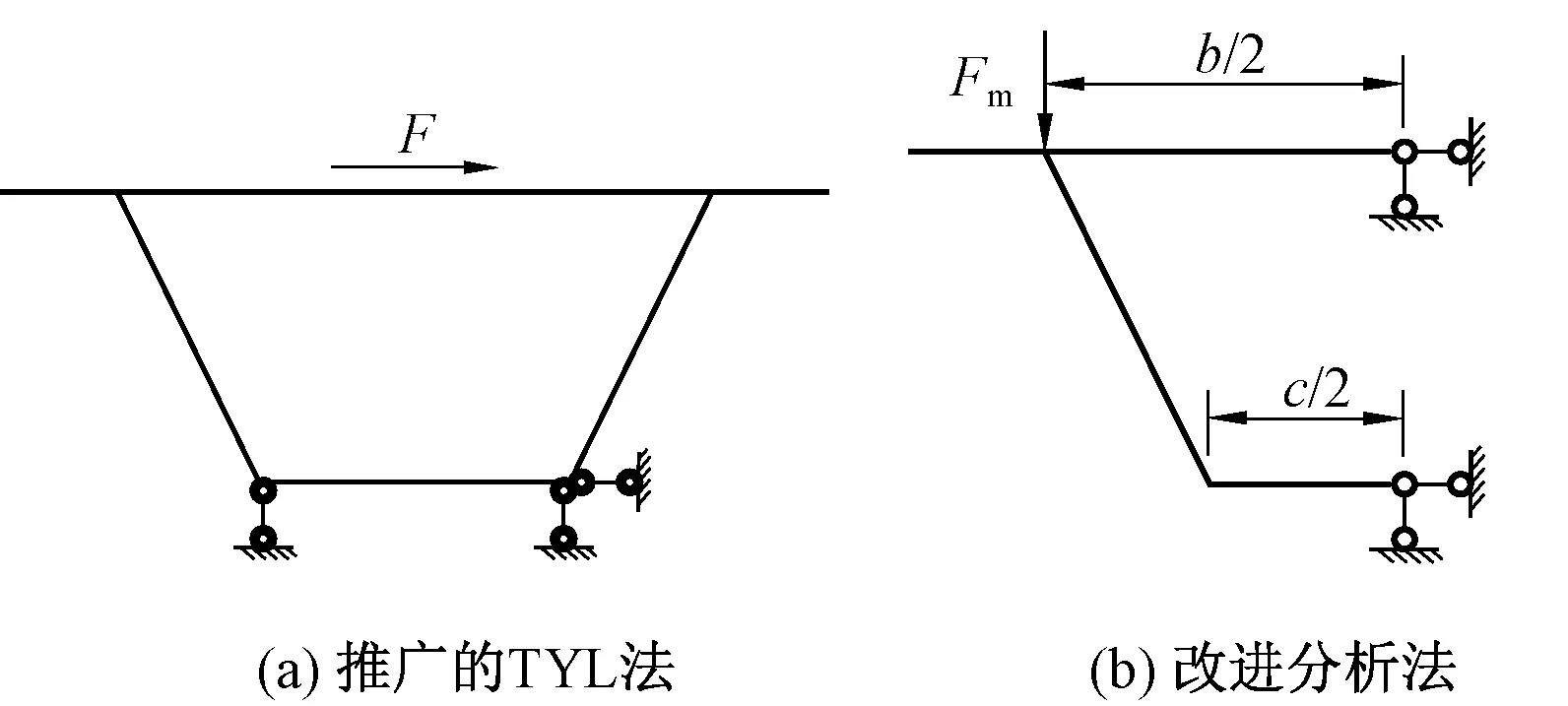
图4 框架计算模型

根据图3和图4(b)，内剪力Qs、Qx和外力Fm在竖直方向的平衡条件可得

Fm=Qs+Qx

(3)

将式(1)、式(2)代入式(3)可得

(4)

在外力Fm的作用下，薄片框架发生了畸变变形，角点A、D的相对竖向位移分别为ΔAy、ΔDy，顶板、底板、腹板的转角分别为γ1、γ2、γ3，见图5。在小变形的情况下γ3≈0，则γ1、γ2为

图5 框架变形图

(5)

(6)

为了与畸变位移相协调，需要计算框架发生变形时角点A和角点D的相对转角γA和γD。变形后角点A和角点D位移至A′和D′处。由几何关系可得

γA=γ1-γ3≈γ1

(7)

γD=γ2-γ3≈γ2

(8)

采用结构力学分析方法，可以求得薄片框架顶板处的内剪力Qs，再由式(1)及式(4)可以求得表示腹板反弯点位置的系数ηm。进一步通过图乘法可以计算得到Fm的作用下薄片框架的相对竖向位移ΔAy、ΔDy分别为

(9)

(10)

采用图4(a)所示的计算模型计算所得的横截面尺寸系数为

(11)

由式(11)可知，当顶、底板长度相同，即b=c时，ηm=ηma，即文献[15]中推广的TYL法只能用来计算直腹板箱梁的横向内力。本文方法在计算斜腹板箱梁的横向内力时更为准确。

箱形梁发生畸变时的变形见图6。

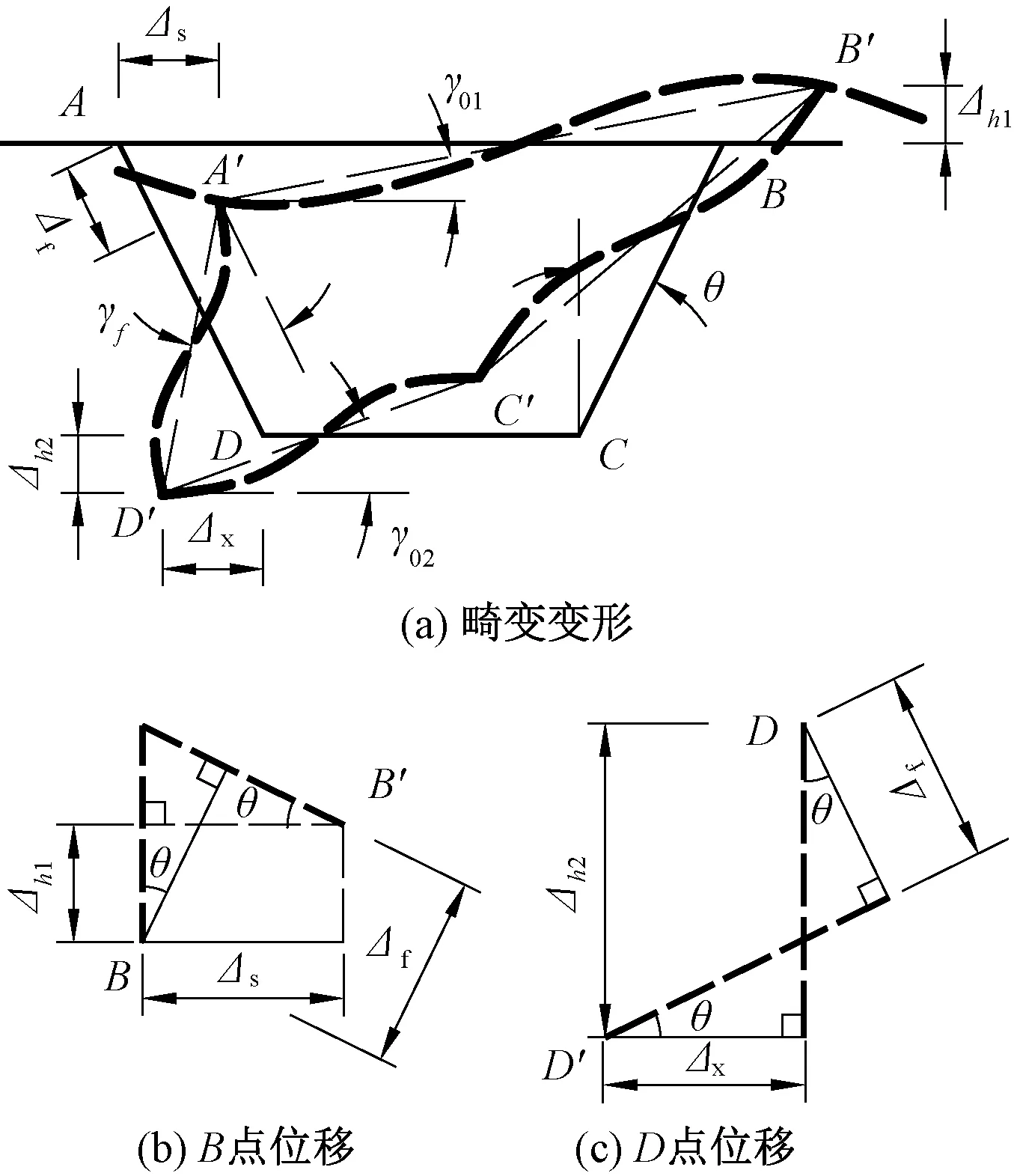
图6 框架畸变变形

在分析箱形梁畸变效应时，一般认为组成箱形梁的各板件在自身平面内的弯曲可按初等梁理论计算。此时，箱形梁横截面上的畸变剪力差与箱梁横截面上各板件的面内位移Δi(i=s，x，f)关系为

(12)

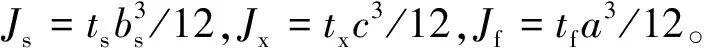
求得各板件面内位移后，根据图6所示的几何关系，可以得到箱形梁各角点处畸变角与面内位移之间关系为

(13)

(14)

(15)

式中：Δh1为B点竖向位移；Δh2为D点竖向位移。

对于同一梁体，在畸变荷载作用下，按照箱形梁畸变理论计算所得的位移应当与按框架理论计算的位移相等。由框架位移与畸变位移的协调关系，可得

γ01+γf=γA

(16)

γ02+γf=γD

(17)

将式(16)、式(17)相加，并将式(7)、式(8)代入，可得

γ01+γ02+2γf=γ1+γ2

(18)

将式(5)、式(6)、式(10)、式(12)～式(15)代入式(18)，可得腹杆上的内剪力Qf为

(19)

1.2 框架内力及荷载的平衡关系

根据箱形梁刚性扭转理论，箱形梁横截面上的剪力流具有连续性，可得

(20)

根据畸变翘曲正应力在横截面的自平衡条件，由初等梁理论可得

(21)

(22)

式中：β为腹板与底板、顶板交点处的翘曲应力之比，可根据畸变翘曲正应力对箱形梁横截面竖向对称轴的自平衡条件求出；αs为薄片框架顶板全宽与箱室顶板宽度之比。

释放虚设支承后，作用在薄片框架上的反力可以分解成正对称荷载qs，水平反对称荷载qh以及竖向反对称荷载qv。根据内剪力和释放虚设支承后反对称荷载的平衡关系，可得

(23)

(24)

至此，联立式(1)、式(2)、式(19)～式(24)，可求得释放虚设支承后反对称荷载引起的横向弯矩。值得指出的是，文献[9]中提出求解横向弯矩需要9个方程，而本文只需8个方程即可求解。

2 数值算例及参数分析

本文采用文献[9]中的算例进行计算。该梁选自宝兰客专双线无咋轨道48 m后张法预应力混凝土简支箱梁桥，该梁混凝土强度为C50，弹性模量为E=3.45 GPa，泊松比μ=0.17，其两端设置厚度为1.2 m的横隔梁，箱形梁横截面尺寸及荷载布置见图7。在计算过程中，将ZK标准活载简化为沿梁跨均匀分布的偏心荷载q=25.77 kN/m2，荷载横向作用宽度为2.8 m。在计算过程中，分别采用本文改进分析法、文献[9]中采用的推广的TYL法以及Ansys有限元分析软件中的壳单元来计算箱形梁的横向弯矩。采用Ansys壳单元计算时，箱梁共离散为个33 072个单元。

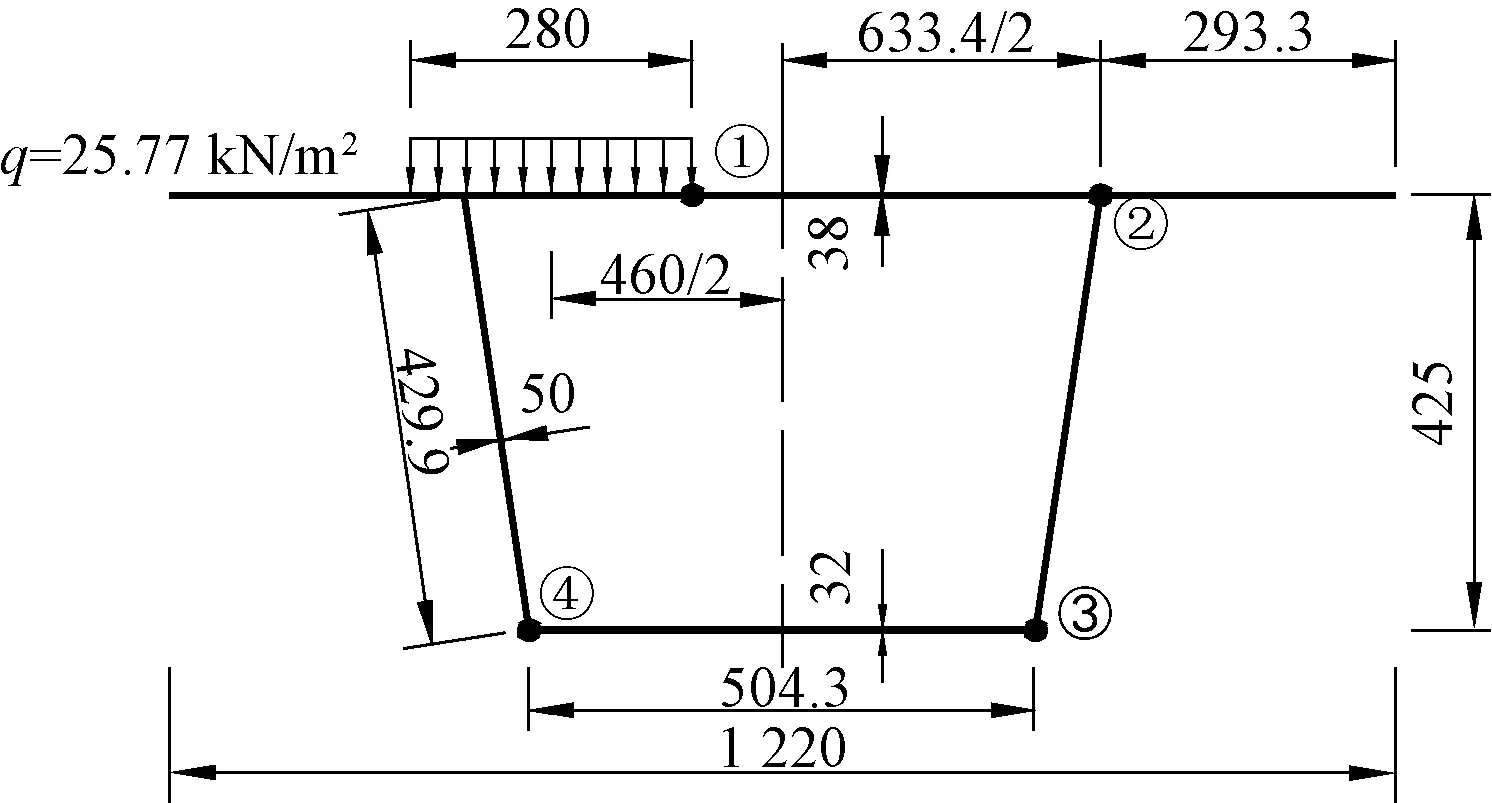
图7 箱形梁横截面简图(单位：cm)

分别按三种不同的方法计算而得的箱形梁横向弯矩，见表1。表1中①、②、③、④分别为横截面上的不同计算点，见图7。由表1可知，采用Ansys有限元法计算所得的横向弯矩与采用本文改进的分析法计算所得的结果更为接近，最大误差为5.22%。而采用推广的“TYL”框架法计算所得的横向弯矩则与Ansys有限元法所得结果相差较大。尤其是在底板上，本文改进的分析法较推广的TYL框架法取得了更高的精度，这进一步说明了改进的分析法的准确性。

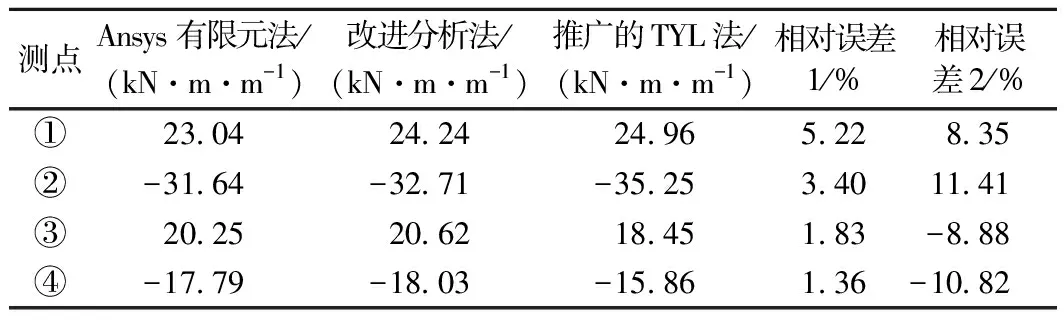
表1 箱梁跨中截面横向弯矩比较

注：相对误差1=(改进分析法-Ansys有限元法)/Ansys有限元法×100%；相对误差2=(推广的YTL法-Ansys有限元法)/Ansys有限元法×100%。

跨中载高计算点②、计算点③处的横向弯矩随箱室底板与顶板宽度之比c/b的变化曲线见图8。在计算过程中，保持箱室顶板的长度b不变，使底板长度逐渐从0.5b增加到1b。由图8可知，与推广的TYL法计算结果相比，在底顶板比c/b变化的过程中，采用本文改进分析法计算的箱形梁横向弯矩与Ansys有限元法计算的结果更为接近，其分布规律也更为相似。特别在底板上，采用推广的TYL法计算所得的横向弯矩分布规律与实际情况不符，不能准确反映横向弯矩的变化规律。当c/b=1.0，即箱形梁为直腹板时，采用本文改进分析方法与推广的TYL法计算所得的结果完全相同，这进一步说明推广的TYL法在计算直腹板箱形梁横向内力时是准确的，而对于斜腹板箱梁，其计算结果误差较大。从图8中还可以看出，计算点②、③处的横向弯矩随底、顶板之比c/b的增大而逐渐增大。因此，适量减小斜腹板箱梁的底板长度可以减小横向内力，从而缓解因横向应力过大而产生的纵向裂缝。

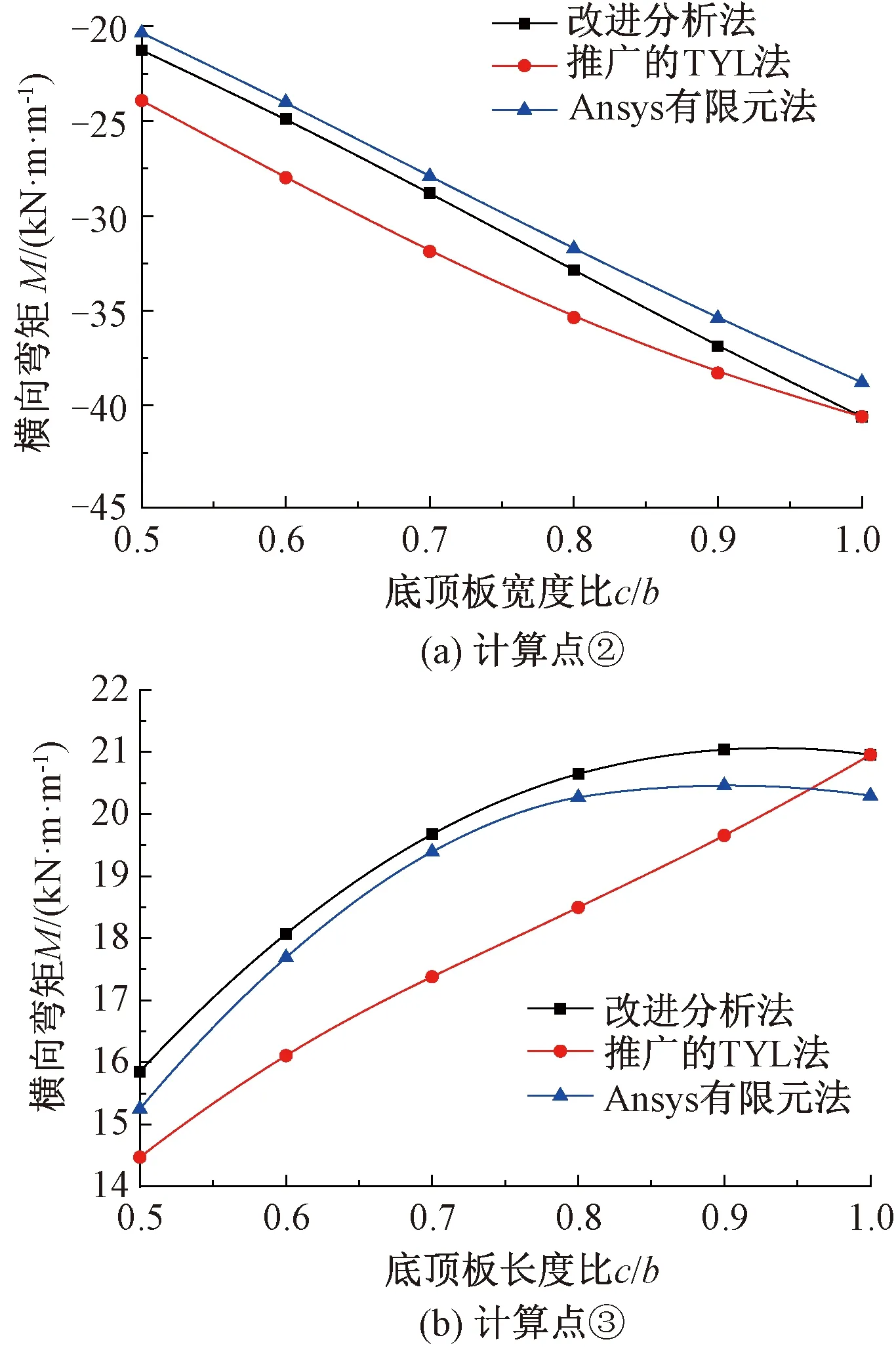
图8 横向弯矩随板宽比的变化

箱形梁顶板上计算点②处的横向弯矩随箱室高度与顶板宽度之比h/b的变化曲线见图9。在计算过程中，保持箱室顶板的宽度b不变，使箱室高度h逐渐从0.5b增加到1.0b。由图9可知，采用本文改进分析法计算所得箱形梁横向弯矩与Ansys有限元结果吻合更好。此外，横截面上的横向弯矩随高宽比h/b的增大而逐渐减小。因此，在不改变箱形梁梁宽的情况下适量增大梁体高度，可以减小横截面上的横向内力。

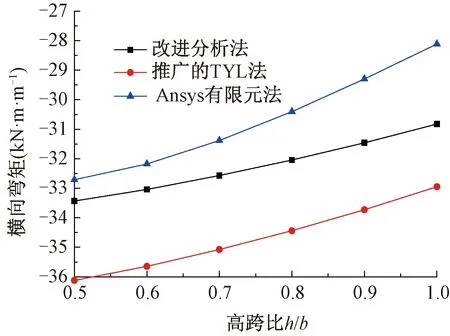
图9 计算点②处横向弯矩随高宽比的变化

3 结论

(1)推广的TYL法只在计算直腹板箱形梁横向内力时是准确的。而当箱形梁为直腹板时，本文改进分析法计算所得结果与推广的TYL法计算所得结果完全相同。

(2)采用推广的TYL法计算所得的箱形梁横向弯矩与Ansys有限元计算结果的相对误差更为显著，尤其在底板上，其分布规律与实际情况不符，不能准确反映横向弯矩的变化规律。而按本文改进分析法计算所得的箱形梁横向弯矩与Ansys有限元法计算的结果在顶、底板上均吻合更好。

(3) 箱形梁横截面上的横向弯矩随底、顶板宽度之比c/b的增大而逐渐增大。因此，适量减小斜腹板箱梁的底板宽度可以减小横向内力，从而缓解因横向应力过大而产生的纵向裂缝。

(4) 横截面上的横向弯矩随高宽比h/b的增大而逐渐减小。因此，在不改变箱形梁梁宽的情况下适量增大梁体高度，可以减小横截面上的横向内力。